- 2021-05-12 发布 |
- 37.5 KB |
- 26页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北师大版数学九年级上册同步课件-3第三章 复习课
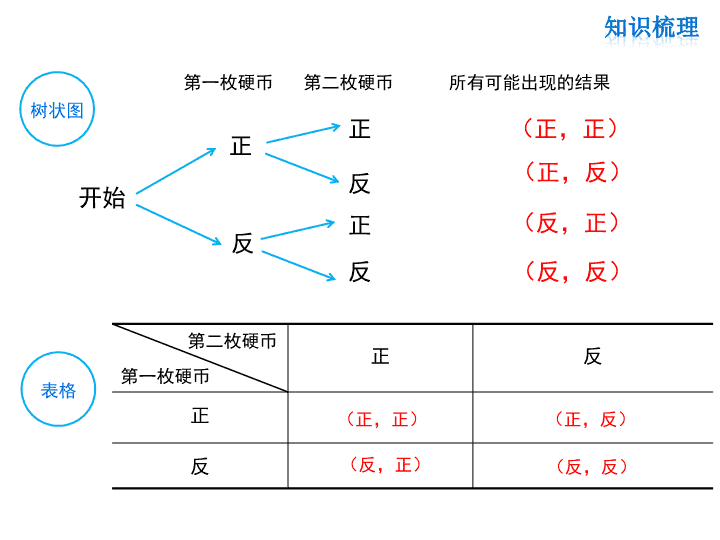
第三章 概率的进一步认识 复习课 1.掷硬币问题 小明、小凡和小颖都想去看周末电影,但只有一张电 影票.三人决定一起做游戏,谁获胜谁就去看电影.游戏规 则如下: 连续抛掷两枚均匀的硬币,如果两枚正面朝上,则小明获 胜;如果两枚反面朝上,则小颖获胜;如果一枚正面朝上、一枚 反面朝上,小凡获胜. 用树状图或表格求概率1 开始 正 正 第一枚硬币 第二枚硬币 所有可能出现的结果 树状图 反 (正,正) (正,反) 反 正 反 (反,正) (反,反) 表格 正 反 正 反 第一枚硬币 第二枚硬币 (正,正) (反,正) (正,反) (反,反) 总共有4种等可能结果, 小明获胜的结果有1种:(正,正), P(小明获胜)= ; 小颖获胜的结果有1种:(反,反),P(小颖获胜)= 小凡获胜的结果有2种:(正,反),(反,正), P(小凡获胜)= = . ∴这个游戏对三人是不公平的. 1 4 1 ;4 2 4 1 2 一只箱子里共有3个球,其中有2个白球,1个红球,它们除 了颜色外均相同. (1)从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸 出一个球,求两次摸出的球都是白球的概率; 1 2 白1 白2 红 白1 —— (白2,白1) (红,白1) 白2 (白1,白2) —— (红,白2) 红 (白1,红) (白2,红) —— 解:(1)列表如下: 第二次 第一次 2.摸球问题 (2)从箱子中任意摸出一个球,将它放回箱子,搅匀后再摸出 一个球,求两次摸出的球都是白球的概率. 1 2 白1 白2 红 白1 (白1,白1) (白2,白1) (红,白1) 白2 (白1,白2) (白2,白2) (红,白2) 红 (白1,红) (白2,红) (红,红) 第二次 第一次 (1)当小球取出后不放入箱子时, 共有6中结果,每个结果的可 能性相同,摸出两个白球概率为 (2)小球取出后放入时,共有9中结果,每种结果的可能性相同, 摸出两个白球概率为 2 1.6 3 4.9 3.配紫游戏 如图示,两个可以自由转动的转盘, 每个转盘被分成面积相等的几个扇 形.红色和蓝色在一起可以配成紫. 能配成紫色的概率是多少? 树状图: 开始 蓝色 红色1 蓝色 红色 A盘 B盘 蓝色 红色 蓝 红色2 蓝色 红色 红蓝1200 红1 蓝 红2 A 盘 B 盘 蓝 列表法: 红色 蓝色 蓝色 (蓝,红) (蓝,红) 红1色 (红1,红) (红1,蓝) 红2色 (红2,红) (红2,蓝) B盘 A盘 1 2 1200 红1 红 蓝 蓝 红2 我们知道,任意抛一枚均匀的硬币,“正面朝上”的概率是0.5, 许多科学家曾做过成千上万次的试验,其中部分结果如下表: 抛掷次数(n) 2048 4040 12000 24000 30000 正面朝上次(m) 1061 2048 6019 12012 14984 频率( ) 0.518 0.506 0.502 0.5005 0.4995 统一条件下,在大量重复试验中,如果事件A发生的频率 稳定与某个常数P,那么事件A发生的概率P(A)=P. m n m n 用频率估计概率2 在中央电视台《星光大道》2015年度冠军总决赛中,甲、 乙、丙三位评委对选手的综合表现,分别给出“待定”或“通 过”的结论. (1)写出三位评委给出A选手的所有可能的结果; (2)对于选手A,只有甲、乙两位评委给出相同结果的概率是 多少? 专题1 用树状图或表格法求概率 例1 解:(1)画出树状图来说明三位评委给出A选手的所有可能结 果如下: 通过 通过 待定 通过 待定 通过 待定 甲 乙 丙 待定 通过 待定 通过 待定 通过 待定 (2)由上图可知,三位评委给出A选手的所有可能的结果共有8 种.对于选手A, “只有甲、乙两位评委给出相同结果”有2种, 即“通过-通过-待定” “待定-待定-通过”,所以对于选手A, “只有甲、乙两位评委给出相同结果”的概率是 .1 4 这个游戏对小亮和小明公平吗? 小明和小亮做扑克游戏,桌面上放有两堆牌,分别是 红桃和黑桃的1,2,3,4,5,6,小明建议:我从红桃中抽取一张牌,你 从黑桃中取一张,当两张牌数字之积为奇数时,你得1分,为 偶数我得1分,先得到10分的获胜.”如果你是小亮,你愿意接受 这个游戏的规则吗? 为什么? 例2 1 2 3 4 5 6 1 2 3 4 5 6 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6) (2,1) (2,2) (2,3) (2,4) (2,5) (2,6) (3,1) (3,2) (3,3) (3,4) (3,5) (3,6) (4,1) (4,2) (4,3) (4,4) (4,5) (4,6) (5,1) (5,2) (5,3) (5,4) (5,5) (5,6) (6,1) (6,2) (6,3) (6,4) (6,5) (6,6) 由表中可以看出,在两堆牌中分别取一张,它可能出现的结果 有36个,它们出现的可能性相等. 因为P(A) < P(B),所以如果我是小亮,我不愿 意接受这个游戏的规则. 满足两张牌的数字之积为奇数(记为事件A) 的有9种情况,所以 9 1( )= .36 4P A 满足两张牌的数字之积为偶数(记为事件B) 的有27种情况,所以 27 3( )= .36 4P B ★用画树状图或列表分析求概率的常用方法: 1.当事件要经过多个步骤完成时,用画树状图法求事件的概 率很有效; 2.一次试验要涉及两个因素,并且可能出现的结果数目较多 时,通常采用列表法分析所有等可能的结果;当结果要求进 行数的和、积等有关运算时,用列表法显得更加清晰、明确. 练习1:一个袋中装有2个黑球,3个白球,这些球除颜色外,大小、 形状、质地完全相同,在看不到球的情况下,随机的从这个袋子 中摸出一个球不放回,再随机的从这个袋子中摸出一个球,两次 摸到的球颜色相同的概率是( ) A. B. C. D. 2 5 3 5 8 2 5 13 25 A 练习2:如图,假设你在每个图形上随机撒一粒黄豆,分别计算 它落到红色部分的概率. 图① 图② 解:图①, 2 1 2 12= . a a P a 图②,设圆的半径为a,则 3= .8P 练习3:如图所示,有3张不透明的卡片,除正面写有不同的数 字外,其他均相同.将这三张卡片背面朝上洗匀后,第一次从 中随机抽取一张,并把这张卡片标有的数字记作一次函数表达 式中的 k,第二次从余下的两张卡片中再随机抽取一张,上面标有的 数字记作一次函数表达式中的b. (1)写出k为负数的概率; (2)求一次函数y=kx+b的图象经过 二、三、四象限的概率. 分析:(1)因为-1,-2,3中有两个负数,故k为负数的 概率为 . (2)由于一次函数y=kx+b的图象经过二、三、四象限时,k, b均为负数,所以在画树形图列举出k、b取值的所有情况后, 从中找出所有k、b均为负数的情况,即可得出答案. 2 3 . (2)画树状图如下: 由树状图可知,k、b的取值共有6种情况,其中k<0且b<0 的情况有2种, ∴P(一次函数y=kx+b的图象经过第二、三、四象限)= 解:(1)P(k为负数)= .2 3 开始 -1 3 -2 -2 3 -1 3 -2 1 2 1.6 3 在大量重复试验中,关于随机事件发生的频率与概率,下 列说法正确的是( ) A.频率就是概率 B.频率与试验次数无关 C.概率是随机的,与频率无关 D.随着试验次数的增加,频率一般会越来越接近概率 D 用频率估计概率专题2 例3 频率是在相同条件下进行重复试验时事件发生的次数与试验总 次数的比值,其本身是随机的,在试验前不能够确定,且随着 试验的不同而发生改变. 而一个随机事件发生的概率是确定的 常数,是客观存在的,与试验次数无关.在大量的重复试验中, 随机事件发生的频率会呈现出明显的规律性:试验频率稳定于 其理论概率. 某篮球运动员在最近的几场大赛中罚球投篮的结果如下: 解:(2)观察这位运动员多次进球的频率可以发现在0.75 上下徘徊,于是可以估计他投篮一次进球的概率是0.75. 投篮次数n 8 10 12 9 16 10 进球次数m 6 8 9 7 12 7 进球率 (1)把表格补充完整; (2)这位运动员投篮一次,进球的概率是多少? 0.75 0.8 0.78 0.70.75 0.75 例4 练习4:在一个不透明的布袋中,红色、黑色、白色的玻璃球 共有40个,除颜色外其他完全相同,小明通过多次摸球试验 后发现从中摸到红色球、黑色球的频率稳定在15%和45%, 则口袋中白色球的个数最有可能是( ) A.24个 B.18个 C.16个 D.6个 C 练习5:在一个不透明的盒子里装有颜色不同的黑、白两种球, 其中白球24个,黑球若干.小兵将盒子里面的球搅匀后从中随机摸 出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下 表是试验中的一组统计数据: 摸球的次数n 100 200 300 500 800 1000 3000 摸到白球次数m 65 124 178 302 481 599 1803 摸到白球概率 0.65 0.62 0.593 0.604 0.601 0.599 0.601n m (1)估计:当n很大时,摸到白球的频率将会接近 .(精确到0.1) (2)假如你摸一次,估计你摸到白球的概率P(白球)= . 0.6 0.6 概 率 的 进 一 步 认 识 简单的随 机事件 复杂的随 机事件 具有等可 能性 不具有等 可能性 树状图 列表 试验法 摸拟试验 理论计算 试验估算 概率定义查看更多