2016年浙江省高考数学试卷（文科）

2016年浙江省高考数学试卷（文科）

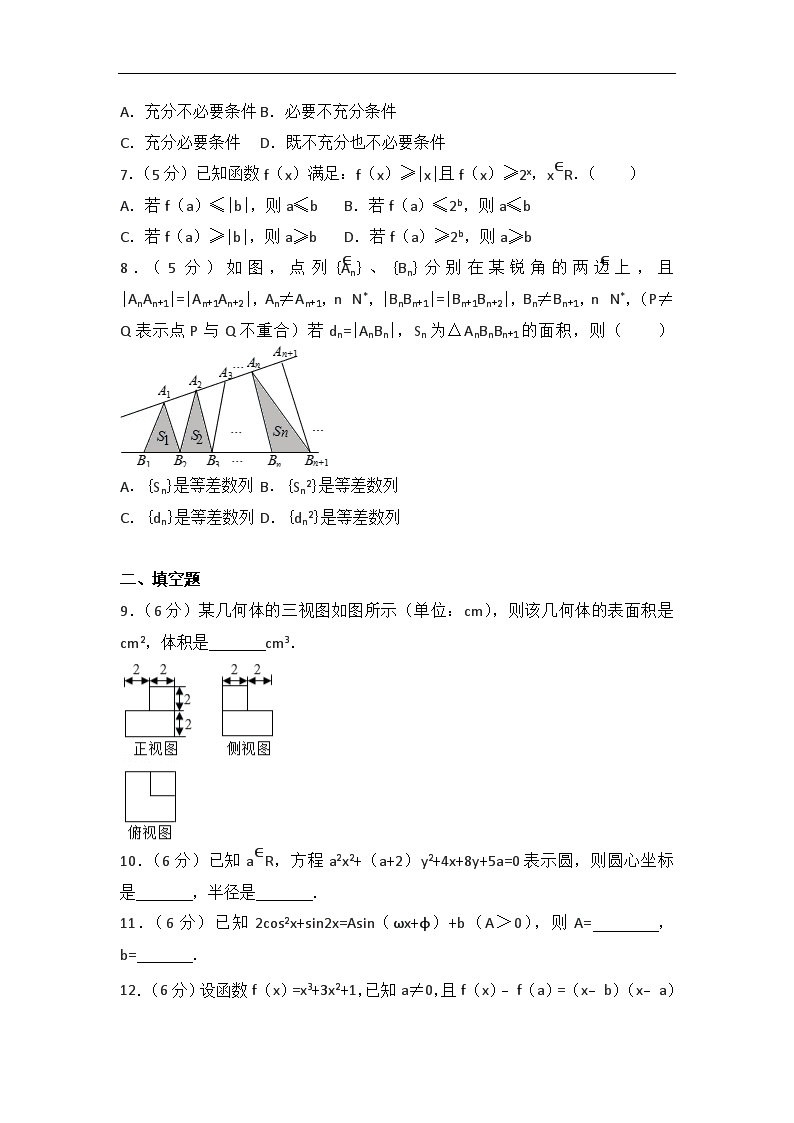
‎2016年浙江省高考数学试卷（文科）‎ ‎　‎ 一、选择题 ‎1．（5分）已知全集U={1，2，3，4，5，6}，集合P={1，3，5}，Q={1，2，4}，则（∁UP）∪Q=（　　）‎ A．{1} B．{3，5} C．{1，2，4，6} D．{1，2，3，4，5}‎ ‎2．（5分）已知互相垂直的平面α，β交于直线l，若直线m，n满足m∥α，n⊥β，则（　　）‎ A．m∥l B．m∥n C．n⊥l D．m⊥n ‎3．（5分）函数y=sinx2的图象是（　　）‎ A． B． C． D．‎ ‎4．（5分）若平面区域，夹在两条斜率为1的平行直线之间，则这两条平行直线间的距离的最小值是（　　）‎ A． B． C． D．‎ ‎5．（5分）已知a，b＞0且a≠1，b≠1，若logab＞1，则（　　）‎ A．（a﹣1）（b﹣1）＜0 B．（a﹣1）（a﹣b）＞0 C．（b﹣1）（b﹣a）＜0 D．（b﹣1）（b﹣a）＞0‎ ‎6．（5分）已知函数f（x）=x2+bx，则“b＜0”是“f（f（x））的最小值与f（x）的最小值相等”的（　　）‎ A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎7．（5分）已知函数f（x）满足：f（x）≥|x|且f（x）≥2x，x∈R．（　　）‎ A．若f（a）≤|b|，则a≤b B．若f（a）≤2b，则a≤b C．若f（a）≥|b|，则a≥b D．若f（a）≥2b，则a≥b ‎8．（5分）如图，点列{An}、{Bn}分别在某锐角的两边上，且|AnAn+1|=|An+1An+2|，An≠An+1，n∈N*，|BnBn+1|=|Bn+1Bn+2|，Bn≠Bn+1，n∈N*，（P≠Q表示点P与Q不重合）若dn=|AnBn|，Sn为△AnBnBn+1的面积，则（　　）‎ A．{Sn}是等差数列 B．{Sn2}是等差数列 C．{dn}是等差数列 D．{dn2}是等差数列 ‎　‎ 二、填空题 ‎9．（6分）某几何体的三视图如图所示（单位：cm），则该几何体的表面积是　 　cm2，体积是　 　cm3．‎ ‎10．（6分）已知a∈R，方程a2x2+（a+2）y2+4x+8y+5a=0表示圆，则圆心坐标是　 　，半径是　 　．‎ ‎11．（6分）已知2cos2x+sin2x=Asin（ωx+φ）+b（A＞0），则A=　 　，b=　 　．‎ ‎12．（6分）设函数f（x）=x3+3x2+1，已知a≠0，且f（x）﹣f（a）=（x﹣b）（x﹣a）‎ ‎2，x∈R，则实数a=　 　，b=　 　．‎ ‎13．（4分）设双曲线x2﹣=1的左、右焦点分别为F1、F2，若点P在双曲线上，且△F1PF2为锐角三角形，则|PF1|+|PF2|的取值范围是　 　．‎ ‎14．（4分）如图，已知平面四边形ABCD，AB=BC=3，CD=1，AD=，∠ADC=90°，沿直线AC将△ACD翻折成△ACD′，直线AC与BD′所成角的余弦的最大值是　 　．‎ ‎15．（4分）已知平面向量，，||=1，||=2，=1，若为平面单位向量，则||+||的最大值是　 　．‎ ‎　‎ 三、解答题 ‎16．（14分）在△ABC中，内角A，B，C所对的边分别为a，b，c，已知b+c=2acosB．‎ ‎（1）证明：A=2B；‎ ‎（2）若cosB=，求cosC的值．‎ ‎17．（15分）设数列{an}的前n项和为Sn，已知S2=4，an+1=2Sn+1，n∈N*．‎ ‎（Ⅰ）求通项公式an；‎ ‎（Ⅱ）求数列{|an﹣n﹣2|}的前n项和．‎ ‎18．（15分）如图，在三棱台ABC﹣DEF中，平面BCFE⊥平面ABC，∠ACB=90°，BE=EF=FC=1，BC=2，AC=3．‎ ‎（Ⅰ）求证：BF⊥平面ACFD；‎ ‎（Ⅱ）求直线BD与平面ACFD所成角的余弦值．‎ ‎19．（15分）如图，设抛物线y2=2px（p＞0）的焦点为F，抛物线上的点A到y轴的距离等于|AF|﹣1，‎ ‎（Ⅰ）求p的值；‎ ‎（Ⅱ）若直线AF交抛物线于另一点B，过B与x轴平行的直线和过F与AB垂直的直线交于点N，AN与x轴交于点M，求M的横坐标的取值范围．‎ ‎20．（15分）设函数f（x）=x3+，x∈[0，1]，证明：‎ ‎（Ⅰ）f（x）≥1﹣x+x2‎ ‎（Ⅱ）＜f（x）≤．‎ ‎　‎ ‎2016年浙江省高考数学试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一、选择题 ‎1．（5分）已知全集U={1，2，3，4，5，6}，集合P={1，3，5}，Q={1，2，4}，则（∁UP）∪Q=（　　）‎ A．{1} B．{3，5} C．{1，2，4，6} D．{1，2，3，4，5}‎ ‎【分析】先求出∁UP，再得出（∁UP）∪Q．‎ ‎【解答】解：∁UP={2，4，6}，‎ ‎（∁UP）∪Q={2，4，6}∪{1，2，4}={1，2，4，6}．‎ 故选：C．‎ ‎【点评】本题考查了集合的运算，属于基础题．‎ ‎　‎ ‎2．（5分）已知互相垂直的平面α，β交于直线l，若直线m，n满足m∥α，n⊥β，则（　　）‎ A．m∥l B．m∥n C．n⊥l D．m⊥n ‎【分析】由已知条件推导出l⊂β，再由n⊥β，推导出n⊥l．‎ ‎【解答】解：∵互相垂直的平面α，β交于直线l，直线m，n满足m∥α，‎ ‎∴m∥β或m⊂β或m与β相交，l⊂β，‎ ‎∵n⊥β，‎ ‎∴n⊥l．‎ 故选：C．‎ ‎【点评】本题考查两直线关系的判断，是基础题，解题时要认真审题，注意空间思维能力的培养．‎ ‎　‎ ‎3．（5分）函数y=sinx2的图象是（　　）‎ A． B． C． D．‎ ‎【分析】根据函数奇偶性的性质，以及函数零点的个数进行判断排除即可．‎ ‎【解答】解：∵sin（﹣x）2=sinx2，‎ ‎∴函数y=sinx2是偶函数，即函数的图象关于y轴对称，排除A，C；‎ 由y=sinx2=0，‎ 则x2=kπ，k≥0，‎ 则x=±，k≥0，‎ 故函数有无穷多个零点，排除B，‎ 故选：D．‎ ‎【点评】本题主要考查函数图象的识别和判断，根据函数奇偶性和函数零点的性质是解决本题的关键．比较基础．‎ ‎　‎ ‎4．（5分）若平面区域，夹在两条斜率为1的平行直线之间，则这两条平行直线间的距离的最小值是（　　）‎ A． B． C． D．‎ ‎【分析】作出平面区域，找出距离最近的平行线的位置，求出直线方程，再计算距离．‎ ‎【解答】解：作出平面区域如图所示：‎ ‎∴当直线y=x+b分别经过A，B时，平行线间的距离相等．‎ 联立方程组，解得A（2，1），‎ 联立方程组，解得B（1，2）．‎ 两条平行线分别为y=x﹣1，y=x+1，即x﹣y﹣1=0，x﹣y+1=0．‎ ‎∴平行线间的距离为d==，‎ 故选：B．‎ ‎【点评】本题考查了平面区域的作法，距离公式的应用，属于基础题．‎ ‎　‎ ‎5．（5分）已知a，b＞0且a≠1，b≠1，若logab＞1，则（　　）‎ A．（a﹣1）（b﹣1）＜0 B．（a﹣1）（a﹣b）＞0 C．（b﹣1）（b﹣a）＜0 D．（b﹣1）（b﹣a）＞0‎ ‎【分析】根据对数的运算性质，结合a＞1或0＜a＜1进行判断即可．‎ ‎【解答】解：若a＞1，则由logab＞1得logab＞logaa，即b＞a＞1，此时b﹣a＞0，b＞1，即（b﹣1）（b﹣a）＞0，‎ 若0＜a＜1，则由logab＞1得logab＞logaa，即b＜a＜1，此时b﹣a＜0，b＜1，即（b﹣1）（b﹣a）＞0，‎ 综上（b﹣1）（b﹣a）＞0，‎ 故选：D．‎ ‎【点评】本题主要考查不等式的应用，根据对数函数的性质，利用分类讨论的数学思想是解决本题的关键．比较基础．‎ ‎　‎ ‎6．（5分）已知函数f（x）=x2+bx，则“b＜0”是“f（f（x））的最小值与f（x）的最小值相等”的（　　）‎ A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎【分析】求出f（x）的最小值及极小值点，分别把“b＜0”和“f（f（x））的最小值与f（x）的最小值相等”当做条件，看能否推出另一结论即可判断．‎ ‎【解答】解：f（x）的对称轴为x=﹣，fmin（x）=﹣．‎ ‎（1）若b＜0，则﹣＞﹣，∴当f（x）=﹣时，f（f（x））取得最小值f（﹣）=﹣，‎ 即f（f（x））的最小值与f（x）的最小值相等．‎ ‎∴“b＜0”是“f（f（x））的最小值与f（x）的最小值相等”的充分条件．‎ ‎（2）设f（x）=t，则f（f（x））=f（t），‎ ‎∴f（t）在（﹣，﹣）上单调递减，在（﹣，+∞）上单调递增，‎ 若f（f（x））=f（t）的最小值与f（x）的最小值相等，‎ 则﹣≤﹣，解得b≤0或b≥2．‎ ‎∴“b＜0”不是“f（f（x））的最小值与f（x）的最小值相等”的必要条件．‎ 故选：A．‎ ‎【点评】本题考查了二次函数的性质，简易逻辑关系的推导，属于基础题．‎ ‎　‎ ‎7．（5分）已知函数f（x）满足：f（x）≥|x|且f（x）≥2x，x∈R．（　　）‎ A．若f（a）≤|b|，则a≤b B．若f（a）≤2b，则a≤b C．若f（a）≥|b|，则a≥b D．若f（a）≥2b，则a≥b ‎【分析】根据不等式的性质，分别进行递推判断即可．‎ ‎【解答】解：A．若f（a）≤|b|，则由条件f（x）≥|x|得f（a）≥|a|，‎ 即|a|≤|b|，则a≤b不一定成立，故A错误，‎ B．若f（a）≤2b，‎ 则由条件知f（x）≥2x，‎ 即f（a）≥2a，则2a≤f（a）≤2b，‎ 则a≤b，故B正确，‎ C．若f（a）≥|b|，则由条件f（x）≥|x|得f（a）≥|a|，则|a|≥|b|不一定成立，故C错误，‎ D．若f（a）≥2b，则由条件f（x）≥2x，得f（a）≥2a，则2a≥2b，不一定成立，即a≥b不一定成立，故D错误，‎ 故选：B．‎ ‎【点评】本题主要考查不等式的判断和证明，根据条件，结合不等式的性质是解决本题的关键．综合性较强，有一定的难度．‎ ‎　‎ ‎8．（5分）如图，点列{An}、{Bn}分别在某锐角的两边上，且|AnAn+1|=|An+1An+2|，An≠An+1，n∈N*，|BnBn+1|=|Bn+1Bn+2|，Bn≠Bn+1，n∈N*，（P≠Q表示点P与Q不重合）若dn=|AnBn|，Sn为△AnBnBn+1的面积，则（　　）‎ A．{Sn}是等差数列 B．{Sn2}是等差数列 C．{dn}是等差数列 D．{dn2}是等差数列 ‎【分析】设锐角的顶点为O，再设|OA1|=a，|OB1|=c，|AnAn+1|=|An+1An+2|=b，|BnBn+1|=|Bn+1Bn+2|=d，由于a，c不确定，判断C，D不正确，设△AnBnBn+1的底边BnBn+1上的高为hn，运用三角形相似知识，hn+hn+2=2hn+1，由Sn=d•hn，可得Sn+Sn+2=2Sn+1，进而得到数列{Sn}为等差数列．‎ ‎【解答】解：设锐角的顶点为O，|OA1|=a，|OB1|=c，‎ ‎|AnAn+1|=|An+1An+2|=b，|BnBn+1|=|Bn+1Bn+2|=d，‎ 由于a，c不确定，则{dn}不一定是等差数列，‎ ‎{dn2}不一定是等差数列，‎ 设△AnBnBn+1的底边BnBn+1上的高为hn，‎ 由三角形的相似可得==，‎ ‎==，‎ 两式相加可得，==2，‎ 即有hn+hn+2=2hn+1，‎ 由Sn=d•hn，可得Sn+Sn+2=2Sn+1，‎ 即为Sn+2﹣Sn+1=Sn+1﹣Sn，‎ 则数列{Sn}为等差数列．‎ 另解：可设△A1B1B2，△A2B2B3，…，AnBnBn+1为直角三角形，‎ 且A1B1，A2B2，…，AnBn为直角边，‎ 即有hn+hn+2=2hn+1，‎ 由Sn=d•hn，可得Sn+Sn+2=2Sn+1，‎ 即为Sn+2﹣Sn+1=Sn+1﹣Sn，‎ 则数列{Sn}为等差数列．‎ 故选：A．‎ ‎【点评】本题考查等差数列的判断，注意运用三角形的相似和等差数列的性质，考查化简整理的推理能力，属于中档题．‎ ‎　‎ 二、填空题 ‎9．（6分）某几何体的三视图如图所示（单位：cm），则该几何体的表面积是　80　cm2，体积是　40　cm3．‎ ‎【分析】根据几何体的三视图，得出该几何体下部为长方体，上部为正方体的组合体，结合图中数据求出它的表面积和体积即可．‎ ‎【解答】解：根据几何体的三视图，得；‎ 该几何体是下部为长方体，其长和宽都为4，高为2，‎ 表面积为2×4×4+2×42=64cm2，体积为2×42=32cm3；‎ 上部为正方体，其棱长为2，‎ 表面积是6×22=24 cm2，体积为23=8cm3；‎ 所以几何体的表面积为64+24﹣2×22=80cm2，‎ 体积为32+8=40cm3．‎ 故答案为：80；40．‎ ‎【点评】本题考查了由三视图求几何体的表面积与体积的应用问题，也考查了空间想象和计算能力，是基础题．‎ ‎　‎ ‎10．（6分）已知a∈R，方程a2x2+（a+2）y2+4x+8y+5a=0表示圆，则圆心坐标是　（﹣2，﹣4）　，半径是　5　．‎ ‎【分析】由已知可得a2=a+2≠0，解得a=﹣1或a=2，把a=﹣1代入原方程，配方求得圆心坐标和半径，把a=2代入原方程，由D2+E2﹣4F＜0说明方程不表示圆，则答案可求．‎ ‎【解答】解：∵方程a2x2+（a+2）y2+4x+8y+5a=0表示圆，‎ ‎∴a2=a+2≠0，解得a=﹣1或a=2．‎ 当a=﹣1时，方程化为x2+y2+4x+8y﹣5=0，‎ 配方得（x+2）2+（y+4）2=25，所得圆的圆心坐标为（﹣2，﹣4），半径为5；‎ 当a=2时，方程化为，‎ 此时，方程不表示圆，‎ 故答案为：（﹣2，﹣4），5．‎ ‎【点评】本题考查圆的一般方程，考查圆的一般方程化标准方程，是基础题．‎ ‎　‎ ‎11．（6分）已知2cos2x+sin2x=Asin（ωx+φ）+b（A＞0），则A=　　，b=　1　．‎ ‎【分析】根据二倍角的余弦公式、两角和的正弦函数化简左边，即可得到答案．‎ ‎【解答】解：∵2cos2x+sin2x=1+cos2x+sin2x ‎=1+（cos2x+sin2x）‎ ‎=sin（2x+）+1，‎ ‎∴A=，b=1，‎ 故答案为：；1．‎ ‎【点评】本题考查了二倍角的余弦公式、两角和的正弦函数的应用，熟练掌握公式是解题的关键．‎ ‎　‎ ‎12．（6分）设函数f（x）=x3+3x2+1，已知a≠0，且f（x）﹣f（a）=（x﹣b）（x﹣a）2，x∈R，则实数a=　﹣2　，b=　1　．‎ ‎【分析】根据函数解析式化简f（x）﹣f（a），再化简（x﹣b）（x﹣a）2，根据等式两边对应项的系数相等列出方程组，求出a、b的值．‎ ‎【解答】解：∵f（x）=x3+3x2+1，‎ ‎∴f（x）﹣f（a）=x3+3x2+1﹣（a3+3a2+1）‎ ‎=x3+3x2﹣（a3+3a2）‎ ‎∵（x﹣b）（x﹣a）2=（x﹣b）（x2﹣2ax+a2）=x3﹣（2a+b）x2+（a2+2ab）x﹣a2b，‎ 且f（x）﹣f（a）=（x﹣b）（x﹣a）2，‎ ‎∴，解得或（舍去），‎ 故答案为：﹣2；1．‎ ‎【点评】本题考查函数与方程的应用，考查化简能力和方程思想，属于中档题．‎ ‎　‎ ‎13．（4分）设双曲线x2﹣=1的左、右焦点分别为F1、F2，若点P在双曲线上，且△F1PF2为锐角三角形，则|PF1|+|PF2|的取值范围是　　．‎ ‎【分析】由题意画出图形，以P在双曲线右支为例，求出∠PF2F1和∠F1PF2为直角时|PF1|+|PF2|的值，可得△F1PF2为锐角三角形时|PF1|+|PF2|的取值范围．‎ ‎【解答】解：如图，‎ 由双曲线x2﹣=1，得a2=1，b2=3，‎ ‎∴．‎ 不妨以P在双曲线右支为例，当PF2⊥x轴时，‎ 把x=2代入x2﹣=1，得y=±3，即|PF2|=3，‎ 此时|PF1|=|PF2|+2=5，则|PF1|+|PF2|=8；‎ 由PF1⊥PF2，得，‎ 又|PF1|﹣|PF2|=2，①‎ 两边平方得：，‎ ‎∴|PF1||PF2|=6，②‎ 联立①②解得：，‎ 此时|PF1|+|PF2|=．‎ ‎∴使△F1PF2为锐角三角形的|PF1|+|PF2|的取值范围是（）．‎ 故答案为：（）．‎ ‎【点评】本题考查双曲线的简单性质，考查双曲线定义的应用，考查数学转化思想方法，是中档题．‎ ‎　‎ ‎14．（4分）如图，已知平面四边形ABCD，AB=BC=3，CD=1，AD=，∠ADC=90°，沿直线AC将△ACD翻折成△ACD′，直线AC与BD′所成角的余弦的最大值是　　．‎ ‎【分析】如图所示，取AC的中点O，AB=BC=3，可得BO⊥AC，在Rt△ACD′中，AC=．作D′E⊥AC，垂足为E，D′E=．CO=，CE==，EO=CO﹣CE=．过点B作BF∥AC，作FE∥BO交BF于点F，则EF⊥AC．连接D′F．∠FBD′为直线AC与BD′所成的角．则四边形BOEF为矩形，BF=EO=．EF=BO=．则∠FED′为二面角D′﹣CA﹣B的平面角，设为θ．利用余弦定理求出D′F2的最小值即可得出．‎ ‎【解答】解：如图所示，取AC的中点O，∵AB=BC=3，∴BO⊥AC，‎ 在Rt△ACD′中，=．‎ 作D′E⊥AC，垂足为E，D′E==．‎ CO=，CE===，‎ ‎∴EO=CO﹣CE=．‎ 过点B作BF∥AC，作FE∥BO交BF于点F，则EF⊥AC．连接D′F．∠FBD′为直线AC与BD′所成的角．‎ 则四边形BOEF为矩形，∴BF=EO=．‎ EF=BO==．‎ 则∠FED′为二面角D′﹣CA﹣B的平面角，设为θ．‎ 则D′F2=+﹣2×cosθ=﹣5cosθ≥，cosθ=1时取等号．‎ ‎∴D′B的最小值==2．‎ ‎∴直线AC与BD′所成角的余弦的最大值===．‎ 也可以考虑利用向量法求解．‎ 故答案为：．‎ ‎【点评】本题考查了空间位置关系、空间角，考查了空间想象能力、推理能力与计算能力，属于难题．‎ ‎　‎ ‎15．（4分）已知平面向量，，||=1，||=2，=1，若为平面单位向量，则||+||的最大值是　　．‎ ‎【分析】由题意可知，||+||为在上的投影的绝对值与在上投影的绝对值的和，由此可知，当与共线时，||+||取得最大值，即．‎ ‎【解答】解：||+||=，‎ 其几何意义为在上的投影的绝对值与在上投影的绝对值的和，‎ 当与共线时，取得最大值．‎ ‎∴=．‎ 故答案为：．‎ ‎【点评】本题考查平面向量的数量积运算，考查向量在向量方向上的投影的概念，考查学生正确理解问题的能力，是中档题．‎ ‎　‎ 三、解答题 ‎16．（14分）在△ABC中，内角A，B，C所对的边分别为a，b，c，已知b+c=2acosB．‎ ‎（1）证明：A=2B；‎ ‎（2）若cosB=，求cosC的值．‎ ‎【分析】（1）由b+c=2acosB，利用正弦定理可得：sinB+sinC=2sinAcosB，而sinC=sin（A+B）=sinAcosB+cosAsinB，代入化简可得：sinB=sin（A﹣B），由A，B∈（0，π），可得0＜A﹣B＜π，即可证明．‎ ‎（II）cosB=，可得sinB=．cosA=cos2B=2cos2B﹣1，sinA=．利用cosC=﹣cos（A+B）=﹣cosAcosB+sinAsinB即可得出．‎ ‎【解答】（1）证明：∵b+c=2acosB，‎ ‎∴sinB+sinC=2sinAcosB，‎ ‎∵sinC=sin（A+B）=sinAcosB+cosAsinB，‎ ‎∴sinB=sinAcosB﹣cosAsinB=sin（A﹣B），由A，B∈（0，π），‎ ‎∴0＜A﹣B＜π，∴B=A﹣B，或B=π﹣（A﹣B），化为A=2B，或A=π（舍去）．‎ ‎∴A=2B．‎ ‎（II）解：cosB=，∴sinB==．‎ cosA=cos2B=2cos2B﹣1=，sinA==．‎ ‎∴cosC=﹣cos（A+B）=﹣cosAcosB+sinAsinB=+×=．‎ ‎【点评】本题考查了正弦定理、和差公式、倍角公式、同角三角函数基本关系式、诱导公式，考查了推理能力与计算能力，属于中档题．‎ ‎　‎ ‎17．（15分）设数列{an}的前n项和为Sn，已知S2=4，an+1=2Sn+1，n∈N*．‎ ‎（Ⅰ）求通项公式an；‎ ‎（Ⅱ）求数列{|an﹣n﹣2|}的前n项和．‎ ‎【分析】（Ⅰ）根据条件建立方程组关系，求出首项，利用数列的递推关系证明数列{an}是公比q=3的等比数列，即可求通项公式an；‎ ‎（Ⅱ）讨论n的取值，利用分组法将数列转化为等比数列和等差数列即可求数列{|an﹣n﹣2|}的前n项和．‎ ‎【解答】解：（Ⅰ）∵S2=4，an+1=2Sn+1，n∈N*．‎ ‎∴a1+a2=4，a2=2S1+1=2a1+1，‎ 解得a1=1，a2=3，‎ 当n≥2时，an+1=2Sn+1，an=2Sn﹣1+1，‎ 两式相减得an+1﹣an=2（Sn﹣Sn﹣1）=2an，‎ 即an+1=3an，当n=1时，a1=1，a2=3，‎ 满足an+1=3an，‎ ‎∴=3，则数列{an}是公比q=3的等比数列，‎ 则通项公式an=3n﹣1．‎ ‎（Ⅱ）an﹣n﹣2=3n﹣1﹣n﹣2，‎ 设bn=|an﹣n﹣2|=|3n﹣1﹣n﹣2|，‎ 则b1=|30﹣1﹣2|=2，b2=|3﹣2﹣2|=1，‎ 当n≥3时，3n﹣1﹣n﹣2＞0，‎ 则bn=|an﹣n﹣2|=3n﹣1﹣n﹣2，‎ 此时数列{|an﹣n﹣2|}的前n项和Tn=3+﹣=，‎ 则Tn==．‎ ‎【点评】本题主要考查递推数列的应用以及数列求和的计算，根据条件建立方程组以及利用方程组法证明列{an}是等比数列是解决本题的关键．求出过程中使用了转化法和分组法进行数列求和．‎ ‎　‎ ‎18．（15分）如图，在三棱台ABC﹣DEF中，平面BCFE⊥平面ABC，∠ACB=90°，BE=EF=FC=1，BC=2，AC=3．‎ ‎（Ⅰ）求证：BF⊥平面ACFD；‎ ‎（Ⅱ）求直线BD与平面ACFD所成角的余弦值．‎ ‎【分析】（Ⅰ）根据三棱台的定义，可知分别延长AD，BE，CF，会交于一点，并设该点为K，并且可以由平面BCFE⊥平面ABC及∠ACB=90°可以得出AC⊥平面BCK，进而得出BF⊥AC．而根据条件可以判断出点E，F分别为边BK，CK的中点，从而得出△BCK为等边三角形，进而得出BF⊥CK，从而根据线面垂直的判定定理即可得出BF⊥平面ACFD；‎ ‎（Ⅱ）由BF⊥平面ACFD便可得出∠BDF为直线BD和平面ACFD所成的角，根据条件可以求出BF=，DF=，从而在Rt△BDF中可以求出BD的值，从而得出cos∠BDF的值，即得出直线BD和平面ACFD所成角的余弦值．‎ ‎【解答】解：（Ⅰ）证明：延长AD，BE，CF相交于一点K，如图所示：∵平面BCFE⊥平面ABC，且AC⊥BC；‎ ‎∴AC⊥平面BCK，BF⊂平面BCK；‎ ‎∴BF⊥AC；‎ 又EF∥BC，BE=EF=FC=1，BC=2；‎ ‎∴△BCK为等边三角形，且F为CK的中点；‎ ‎∴BF⊥CK，且AC∩CK=C；‎ ‎∴BF⊥平面ACFD；‎ ‎（Ⅱ）∵BF⊥平面ACFD；‎ ‎∴∠BDF是直线BD和平面ACFD所成的角；‎ ‎∵F为CK中点，且DF∥AC；‎ ‎∴DF为△ACK的中位线，且AC=3；‎ ‎∴；‎ 又；‎ ‎∴在Rt△BFD中，，cos；‎ 即直线BD和平面ACFD所成角的余弦值为 ‎【点评】‎ 考查三角形中位线的性质，等边三角形的中线也是高线，面面垂直的性质定理，以及线面垂直的判定定理，线面角的定义及求法，直角三角形边的关系，三角函数的定义．‎ ‎　‎ ‎19．（15分）如图，设抛物线y2=2px（p＞0）的焦点为F，抛物线上的点A到y轴的距离等于|AF|﹣1，‎ ‎（Ⅰ）求p的值；‎ ‎（Ⅱ）若直线AF交抛物线于另一点B，过B与x轴平行的直线和过F与AB垂直的直线交于点N，AN与x轴交于点M，求M的横坐标的取值范围．‎ ‎【分析】（Ⅰ）利用抛物线的性质和已知条件求出抛物线方程，进一步求得p值；‎ ‎（Ⅱ）设出直线AF的方程，与抛物线联立，求出B的坐标，求出直线AB，FN的斜率，从而求出直线BN的方程，根据A、M、N三点共线，可求出M的横坐标的表达式，从而求出m的取值范围．‎ ‎【解答】解：（Ⅰ）由题意可得，抛物线上点A到焦点F的距离等于A到直线x=﹣1的距离，‎ 由抛物线定义得，，即p=2；‎ ‎（Ⅱ）由（Ⅰ）得，抛物线方程为y2=4x，F（1，0），可设（t2，2t），t≠0，t≠±1，‎ ‎∵AF不垂直y轴，‎ ‎∴设直线AF：x=sy+1（s≠0），‎ 联立，得y2﹣4sy﹣4=0．‎ y1y2=﹣4，‎ ‎∴B（），‎ 又直线AB的斜率为，故直线FN的斜率为，‎ 从而得FN：，直线BN：y=﹣，‎ 则N（），‎ 设M（m，0），由A、M、N三点共线，得，‎ 于是m==，得m＜0或m＞2．‎ 经检验，m＜0或m＞2满足题意．‎ ‎∴点M的横坐标的取值范围为（﹣∞，0）∪（2，+∞）．‎ ‎【点评】本题考查抛物线的简单性质，考查直线与圆锥曲线位置关系的应用，考查数学转化思想方法，属中档题．‎ ‎　‎ ‎20．（15分）设函数f（x）=x3+，x∈[0，1]，证明：‎ ‎（Ⅰ）f（x）≥1﹣x+x2‎ ‎（Ⅱ）＜f（x）≤．‎ ‎【分析】（Ⅰ）根据题意，1﹣x+x2﹣x3=，利用放缩法得≤，即可证明结论成立；‎ ‎（Ⅱ）利用0≤x≤1时x3≤x，证明f（x）≤，再利用配方法证明f（x）≥，结合函数的最小值得出f（x）＞，即证结论成立．‎ ‎【解答】解：（Ⅰ）证明：因为f（x）=x3+，x∈[0，1]，‎ 且1﹣x+x2﹣x3==，‎ 所以≤，‎ 所以1﹣x+x2﹣x3≤，‎ 即f（x）≥1﹣x+x2；‎ ‎（Ⅱ）证明：因为0≤x≤1，所以x3≤x，‎ 所以f（x）=x3+≤x+=x+﹣+=+≤；‎ 由（Ⅰ）得，f（x）≥1﹣x+x2=+≥，‎ 且f（）=+=＞，‎ 所以f（x）＞；‎ 综上，＜f（x）≤．‎ ‎【点评】本题主要考查了函数的单调性与最值，分段函数等基础知识，也考查了推理与论证，分析问题与解决问题的能力，是综合性题目．‎ ‎　‎