2012年台湾中考数学试卷

2012年台湾中考数学试卷

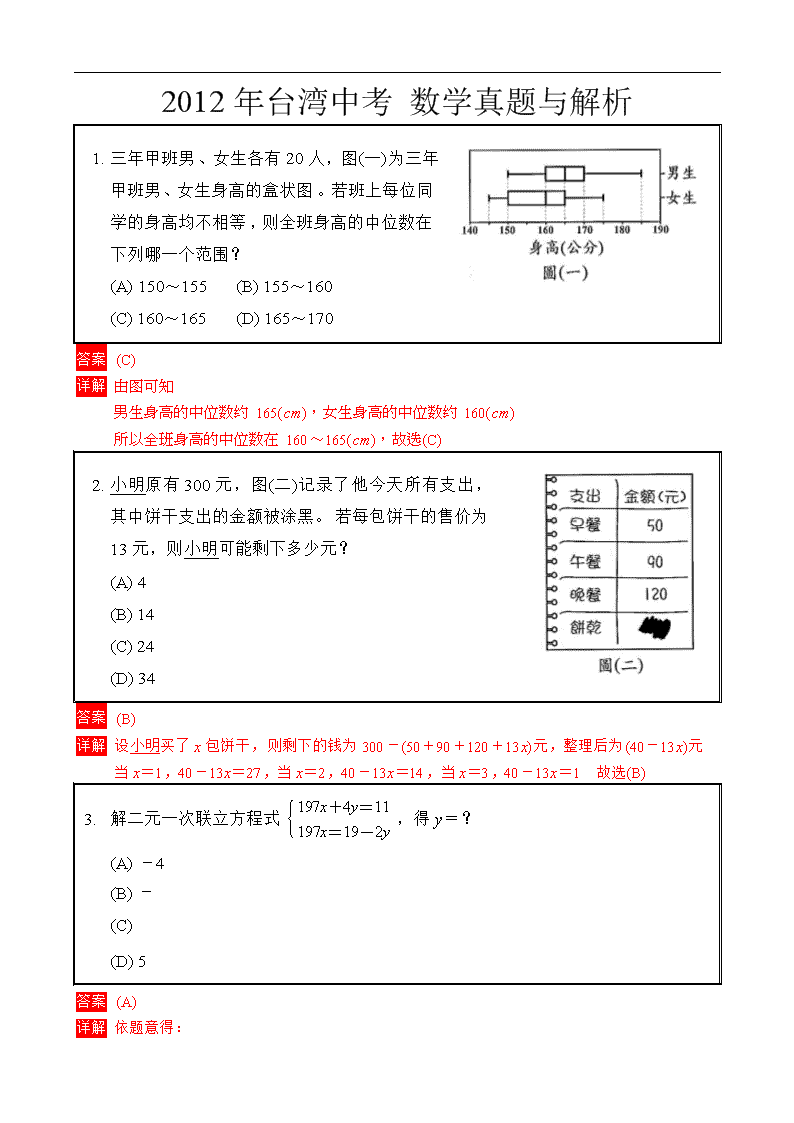
‎2012年台湾中考 数学真题与解析 ‎ 1. 三年甲班男、女生各有20人，图(一)为三年甲班男、女生身高的盒状图。若班上每位同学的身高均不相等，则全班身高的中位数在下列哪一个范围？ (A) 150～155 (B) 155～160 (C) 160～165 (D) 165～170‎ 答案 (C)‎ 详解 由图可知 男生身高的中位数约165(cm)，女生身高的中位数约160(cm) 所以全班身高的中位数在160～165(cm)，故选(C) ‎ ‎ 2. 小明原有300元，图(二)记录了他今天所有支出，其中饼干支出的金额被涂黑。若每包饼干的售价为13元，则小明可能剩下多少元？ (A) 4 (B) 14 (C) 24 (D) 34‎ 答案 (B)‎ 详解 设小明买了x包饼干，则剩下的钱为300－(50＋90＋120＋13x)元，整理后为(40－13x)元 当x＝1，40－13x＝27，当x＝2，40－13x＝14，当x＝3，40－13x＝1 故选(B)‎ ‎3. 解二元一次联立方程式，得y＝？ (A) －4 (B) － (C) (D) 5‎ 答案 (A)‎ 详解 依题意得： ‎ ‎ Þ 由－得：2y＝－8，y＝－4 故选(A)‎ ‎ 4. 已知甲、乙、丙三数，甲＝5＋，乙＝3＋，丙=1＋，则甲、乙、丙的大小关系，下列何者正确？ (A) 丙＜乙＜甲 (B) 乙＜甲＜丙 (C) 甲＜乙＜丙 (D) 甲＝乙＝丙 答案 (A)‎ 详解 3＝＜＜＝4 Þ ＝3.… Þ 甲＝5＋＝8.… 4＝＜＜＝5 Þ ＝4.… Þ 乙＝3＋＝7.… 4＝＜＜＝5 Þ ＝4.… Þ 丙＝1＋＝5.… ∴丙＜乙＜甲 故选(A)‎ ‎ 5. 小美将某服饰店的促销活动内容告诉小明后，小明假设某一商品的定价为x元，并列出关系式为0.3(2x－100)＜1000，则下列何者可能是小美告诉小明的内容？ (A) 买两件等值的商品可减100元，再打3折，最后不到1000元耶！ (B) 买两件等值的商品可减100元，再打7折，最后不到1000元耶！ (C) 买两件等值的商品可打3折，再减100元，最后不到1000元耶！ (D) 买两件等值的商品可打7折，再减100元，最后不到1000元耶！‎ 答案 (A)‎ 详解 由关系式可知 2x－100 Þ 两件商品减100元 0.3 Þ 打3折 ＜1000 Þ 不到1000元 所以0.3(2x－100)＜1000即为 两件商品减100元打3折不到1000元 故选(A)‎ ‎6. 图(三)是利用短除法求出三数8、12、18的最大公因子 的过程。利用短除法，求出这三数的最小公倍数为何？ (A) 12 (B) 72 (C) 216 (D) 432‎ 答案 (B)‎ 详解 完成短除法如下 8、12、18的最小公倍数为2×3×2×2×1×3＝72 故选(B)‎ ‎ 7. 已知某公司去年的营业额为四千零七十亿元，则此营业额可用下列何者表示？ (A) 4.07×109元 (B) 4.07×1010元 (C) 4.07×1011元 (D) 4.07×1012元 答案 (C)‎ 详解 四千零七十亿元可写成407000000000 407000000000＝4.07×1011 故选(C)‎ ‎ 8. 图(四)为制作果冻的食谱，傅妈妈想依此食谱内容制作六人份的果冻。若她加入‎50克砂糖后，不足砂糖可依比例换成糖浆，则她需再加几小匙糖浆？ (A) 15 (B) 18 (C) 21 (D) 24‎ 答案 (C)‎ 详解 六人份需20×6＝120克砂糖， 尚需120－50＝70克砂糖 又20克砂糖＝6小匙糖浆， 所求＝70×＝21(小匙) 故选(C)‎ ‎ 9. 图(五)的方格纸上有一平行四边形ABCD，其顶点均在网格线的交点上，且E点在上。今大华在方格纸网格线的交点上任取一点F，发现△FBC的面积比△EBC的面积大。判断下列哪一个图形可表示大华所取F点的位置？‎ ‎ (A) (B) (C) (D) ‎ 答案 (D)‎ 详解 由(A)、(B)、(C)、(D)四个图可知，(D)图上的F点到的距离＞E点到的距离 所以△FBC的面积＞△EBC的面积 故选(D)‎ ‎10. 小明将一正方形纸片画分成16个全等的小正方形，且图(六)为他将其中四个小正方形涂成灰色的情形。若小明想再将一小正方形涂成灰色，使此纸片上的灰色区域成为线对称图形，则此小正方形的位置为何？ (A)第一列第四行 (B)第二列第一行 (C)第三列第三行 (D)第四列第一行 答案 (B)‎ 详解 完成线对称图形如右 则涂成灰色的小方格在第二列第一行 故选(B)‎ ‎11. 图(七)的直线AE与四边形ABCD的外接圆相切于A点。若∠DAE＝12°，、、三弧的度数相等，则∠ABC的度数为何？ (A) 64 (B) 65 (C) 67 (D) 68‎ 答案 (D)‎ 由∠DAE＝12° 得＝12°×2＝24° ∵＝＝，∴＝(360°－24°)÷3＝112° ∠ABC＝(＋)＝(24°＋112°)＝68°，故选(D)‎ ‎12. 一纸箱内有红、黄、蓝、绿四种颜色的纸牌，且图(八)为各颜色纸牌数量的统计图。若小华自箱内抽出一张牌，且每张牌被抽出的机会相等，则他抽出红色牌或黄色牌的机率为何？ (A) (B) (C) (D) 答案 (B)‎ 抽出红色牌机率＝＝ 抽出黄色牌机率＝＝ 所求＝ ‎＋＝ 故选(B)‎ ‎13. 计算(－1000)×(5－10)之值为何？ (A) 1000 (B) 1001 (C) 4999 (D) 5001‎ 答案 (D)‎ (－1000)×(5－10)＝－(1000＋)×(－5) (－1000)×(5－10)＝1000×5＋×5 (－1000)×(5－10)＝5001 故选(D)‎ ‎14. 下列四个选项中，哪一个为多项式8x2－10x＋2的因式？ (A) 2x－2 (B) 2x＋2 (C) 4x＋1 (D) 4x＋2‎ 答案 (A)‎ 详解 8x2－10x＋2＝2(4x2－5x＋1)＝2(4x－1)(x－1)＝(4x－1)(2x－2) 故选(A) 另解： 分别将8x2－10x＋2除以四个选项 可得(A)(8x2－10x＋2)÷(2x－2)＝4x－1 故选(A)‎ ‎15. 如图(九)，大、小两圆的圆心均为O点，半径分别为3、2，且A点为小圆上的一固定点。若在大圆上找一点B，使得＝，则满足上述条件的B点共有几个？ ‎ ‎(A) 0 (B) 1 (C) 2 (D) 3‎ 答案 (C)‎ 详解 如右图 连，以A点为圆心，为半径画弧，交大圆于B1、B2两点 则B1、B2即为所求(＝＝) ∴满足条件的B点共有2个 故选(C)‎ ‎16. 如图(十)，△ABC中，＝＝17，＝16， M是△ABC的重心，求的长度为何？ (A) 8 (B) 10 (C) (D) 答案 (B)‎ 详解 如右图，延长，交于N点 ∵＝ Þ △ABC为等腰三角形 又M是△ABC的重心　∴为中线，且⊥ ∴＝＝＝8 ＝＝15 ＝＝×15＝10 故选(B)‎ ‎17. 图(十一)为魔术师在小美面前表演的经过： 根据图(十一)，假设小美在纸上写的数字为x，魔术师猜中的答案为y，则下列哪一个图形可以表示x、y的关系？‎ ‎ (A) (B) (C) (D)‎ 答案 (B)‎ 详解 由数字乘以3可得3x 　加6可得3x＋6 　结果除以3可得(3x＋6)÷3＝x＋2 　再减去一开始写的数字可得x＋2－x＝2 ∴可得x、y的关系式为y＝2 故选(B) ‎ ‎18. 判断下列哪一组的a、b、c，可使二次函数y＝ax2＋bx＋c－5x2－3x＋7在坐标平面上的图形有最低点？ (A) a＝0，b＝4，c＝8 (B) a＝2，b＝4，c＝－8 (C) a＝4，b＝－4，c＝8 (D) a＝6，b＝－4，c＝－8‎ 答案 (D)‎ 详解 y＝ax2＋bx＋c－5x2－3x＋7 y＝(a－5)x2＋(b－3)x＋(c＋7) 若此二次函数图形有最低点 则图形的开口向上 Þ x2项系数为正数 Þ a－5＞0，a＞5 故选(D)‎ ‎19. 图(十二)数在线的A、B、C、D四点所表示的数分别为a、b、c、d，且O为原点。根据图中各点位置，判断｜a－c｜之值与下列何者不同？ (A) ｜a｜＋｜b｜＋｜c｜ (B) ｜a－b｜＋｜c－b｜ (C) ｜a－d｜－｜d－c｜ (D) ｜a｜＋｜d｜－｜c－d｜‎ 答案 (A)‎ 详解 ｜a－c｜＝ (A)｜a｜＋｜b｜＋｜c｜＝＋＋≠ (B)｜a－b｜＋｜c－b｜＝＋＝ (C)｜a－d｜－｜d－c｜＝－＝ (D)｜a｜＋｜d｜－｜c－d｜＝＋－＝ 故选(A)‎ ‎20. 表(一)为某公司200名职员年龄的次数分配表，其中36～42岁及50～56岁的次数因污损而无法看出。若36～42岁及50～56岁职员人数的相对次数分别为a%、b%，则a＋b之值为何？ (A) 10 (B) 45 (C) 55 (D) 99‎ 答案 (C)‎ 详解 由表知36～42岁及50～56岁的职员人数 共有200－6－40－42－2＝110人 a%＋b%＝ ×100%＝55% Þ a＋b＝55 故选(C)‎ ‎21. 图(十三)正六边形ABCDEF的边长为1，连接、、，求图中灰色四边形的周长为何？ (A) 3 (B) 4 (C) 2＋ (D) 2＋ 答案 (D)‎ 详解 如右图 ∵ABCDEF为正六边形 ∴∠ABC＝120°，∠CBG＝60° 又＝1(＝＝) ∴＝(＝) 四边形CDHG的周长＝(1＋)×2＝2＋ 故选(D)‎ ‎22. 有一段树干为一直圆柱体，其底面积为9π平方公尺，高为15公尺。若将此树干分为两段圆柱形树干，且体积比为2：1，则体积较大的树干，其侧面的表面积为多少平方公尺？ (A) 60π (B) 72π (C) 84π (D) 96π 答案 (A)‎ 详解 ∵两段圆柱形树干的体积比为2：1 ∴两段圆柱形树干的柱高比为2：1 则体积较大的树干柱高为15×＝10(公尺) ∵圆柱体的底面积为9π平方公尺 ∴圆柱体的底圆半径为3公尺 所求＝(2×π×3)×10＝60π(平方公尺) 故选(A)‎ ‎ ‎ ‎23. 计算[()2]3×[()2]2之值为何？ ‎ ‎(A) 1 (B) (C) ()2 (D) ()4‎ 答案 (C)‎ 原式＝()6×[()－2]2　　　(∵＝()－1　∴()2＝[()－1]2＝()－2) 　　＝()6×()－4 　　＝()6－4＝()2 故选(C)‎ ‎24. 小华带x元去买甜点，若全买红豆汤圆刚好可买30杯，若全买豆花刚好可买40杯。已知豆花每杯比红豆汤圆便宜10元，依题意可列出下列哪一个方程式？ (A) ＝＋10 (B) ＝＋10 (C) ＝ (D) ＝ 答案 (A)‎ 由题意知红豆汤圆每杯元，豆花每杯元 又豆花每杯比红豆汤圆便宜10元 即＝－10 Þ ＝＋10 故选(A)‎ ‎25. 如图(十四)，坐标平面上直线L的方程式为3x－y＝－3。若有一直线L¢的方程式为y＝a，则a的值在下列哪一个范围时，L¢与L的交点会在第二象限？ (A) 1＜a＜2 (B) 3＜a＜4 (C) －1＜a＜0 ‎ ‎(D) －3＜a＜－2‎ 答案 (A)‎ 详解 由L：3x－y＝－3可知，由L交y轴于(0 , 3)，由图可知当0＜a＜3时 L¢与L的交点会在第二象限，故选(A)‎ ‎26. 计算之值为何？ (A) 0 (B) 25 (C) 50 (D) 80‎ 答案 (D)‎ 详解 ＝=＝ ＝ ＝＝ ＝＝24×5＝80，故选(D)‎ ‎27. 图(十五)为图(十六)中三角柱ABCEFG的展开图，其中、、、是三角柱的边。若图(十五)中，＝10，＝2，则下列何者可为长度？ 　　　　　 (A) 2 (B) 3 (C) 4 (D) 5‎ 答案 (C)‎ 详解 设＝x，＝8－x 则x－2＜8－x＜x＋2 由8－x＜x＋2得x＞3 由x－2＜8－x得x＜5 Þ 3＜x＜5 故选(C)‎ ‎28. 如图(十七)，一圆桌周围有20个箱子，依顺时针方向编号1～20。小明在1‎ 号箱子中丢入一颗红球后，沿着圆桌依顺时针方向行走，每经过一个箱子就依下列规则丢入一颗球： 1. 若前一个箱子丢红球，经过的箱子就丢绿球。 2. 若前一个箱子丢绿球，经过的箱子就丢白球。 3. 若前一个箱子丢白球，经过的箱子就丢红球。‎ ‎ 已知他沿着圆桌走了100圈，求4号箱内有几颗红球？ (A) 33 (B) 34 (C) 99 (D) 100‎ 答案 (B)‎ 详解 第1圈红球在1、、7、10、13、16、19号箱内 第2圈红球在2、5、8、11、14、17、20号箱内 第3圈红球在3、6、9、12、15、18号箱内 第4圈红球在1、、7、10、13、16、19号箱内 … 且第1、4、7、……、100圈会在4号箱内丢一颗红球 an＝a1＋(n－1)d 100＝1＋3(n－1) 33＝n－1 n＝34 故选(B)‎ ‎29. 如图(十八)，梯形ABCD中，∠DAB＝∠ABC＝90°，E点在上，且：＝1：4。若＝5，＝4，＝8，则四边形ABCE的面积为何？ (A) 24 (B) 25 (C) 26 (D) 27‎ 答案 (C)‎ 详解 如右图，连 梯形ABCD面积＝＝30 △ABC面积＝×5×4＝10 △ACD面积＝30－10＝20 ∵：＝1：4 ∴△ACE面积＝20×＝16 ∴四边形ABCE面积＝10＋16＝26 故选(C)‎ ‎30. 有一个二次函数y＝x2＋ax＋b，其中a、b为整数。已知此函数在坐标平面上的图形与x轴交于两点，且两交点的距离为4。若此图形的对称轴为x＝－5，则此图形通过下列哪一点？ (A) (－6 , －1) (B) (－6 , －2) (C) (－6 , －3) (D) (－6 , －4)‎ 答案 (C)‎ 详解 ∵二次函数图形的对称轴为x＝－5 又图形与x轴的两个交点距离为4 ∴此两点的坐标为(－7 , 0)和(－3 , 0) 设二次函数y＝(x＋7)(x＋3) 将x＝－6代入，得y＝(－6＋7)(－6＋3)＝－3 Þ 图形会通过点(－6 , －3) 故选(C)‎ ‎31. 若一元二次方程式x2－2x－3599＝0的两根为a、b，且a＞b，则‎2a－b之值为何？ (A) －57 (B) 63 (C) 179 (D) 181‎ 答案 (D)‎ 详解 x2－2x－3599＝0 Þ x2－2x＝3599 Þ x2－2x＋1＝3599＋1 Þ (x－1)2＝3600 Þ x－1＝60或x－1＝－60 ∴x＝61或x＝－59 又a＞b，∴a＝61，b＝－59 Þ 2a－b＝2×61－(－59)＝181 故选(D)‎ ‎32. 如图(十九)，边长12的正方形ABCD中，有一个小正方形EFGH，其中E、F、G分别在、、上。若＝3，则小正方形的边长为何？ (A) 正 (B) 正 (C) 5正 (D) 6正 答案 (B)‎ 详解 在△BEF与△CFD中 ∠1＋∠2＝∠2＋∠3＝90° Þ ∠1＝∠3 且∠B＝∠C＝90°，∴△BEF～△CFD(AA相似) 又＝＝＝15 ∴ ＝，＝ Þ ＝ 故选(B)‎ ‎33. 如图(廿)，直角三角形ABC有一外接圆，其中∠B＝90°，　　‎ ＞，今欲在上找一点P，使得＝，以下是甲、乙两人的作法： (甲) 1. 取中点D 2. 过D作直线AC的并行线，交于P，则P即为所求 (乙) 1. 取中点E 2. 过E作直线AB的并行线，交于P，则P即为所求 对于甲、乙两人的作法，下列判断何者正确？ ‎ ‎ (A) 两人皆正确 (B) 两人皆错误 (C) 甲正确，乙错误 (D) 甲错误，乙正确 答案 (D)‎ (1) 由甲的作法，可知≠ (2) 由乙的作法，连 可知△BEC为等腰三角形 又直线PE⊥，∴∠1＝∠2 故＝ ∴甲错误，乙正确 故选(D)‎ ‎34. 图(廿一)的长方形ABCD中，E点在上，且＝2。今分别以、为折线，将A、D向的方向折过去，图(廿二)为对折后A、B、C、D、E 五点均在同一平面上的位置图。若图(廿二)中，∠AED＝15°，则∠BCE的度数为何？ 　　　　　　 (A) 30 (B) 32.5 (C) 35 (D) 37.5‎ 答案 (D)‎ 详解 ∵＝2＝2，∠A＝∠A¢＝90° ∴△ABE、△A¢BE皆为30°、60°、90° 的三角形 Þ ∠1＝∠AEB＝60°，∠AED¢＝180°－60°－60°＝60° Þ ∠DED¢＝∠AED＋∠AED¢＝15°＋60°＝75° Þ ∠2＝∠DED¢＝37.5° ∴∠BCE＝37.5° 故选(D)‎