【数学】2020届一轮复习人教版（理）第9章第2讲用样本估计总体作业

【数学】2020届一轮复习人教版（理）第9章第2讲用样本估计总体作业

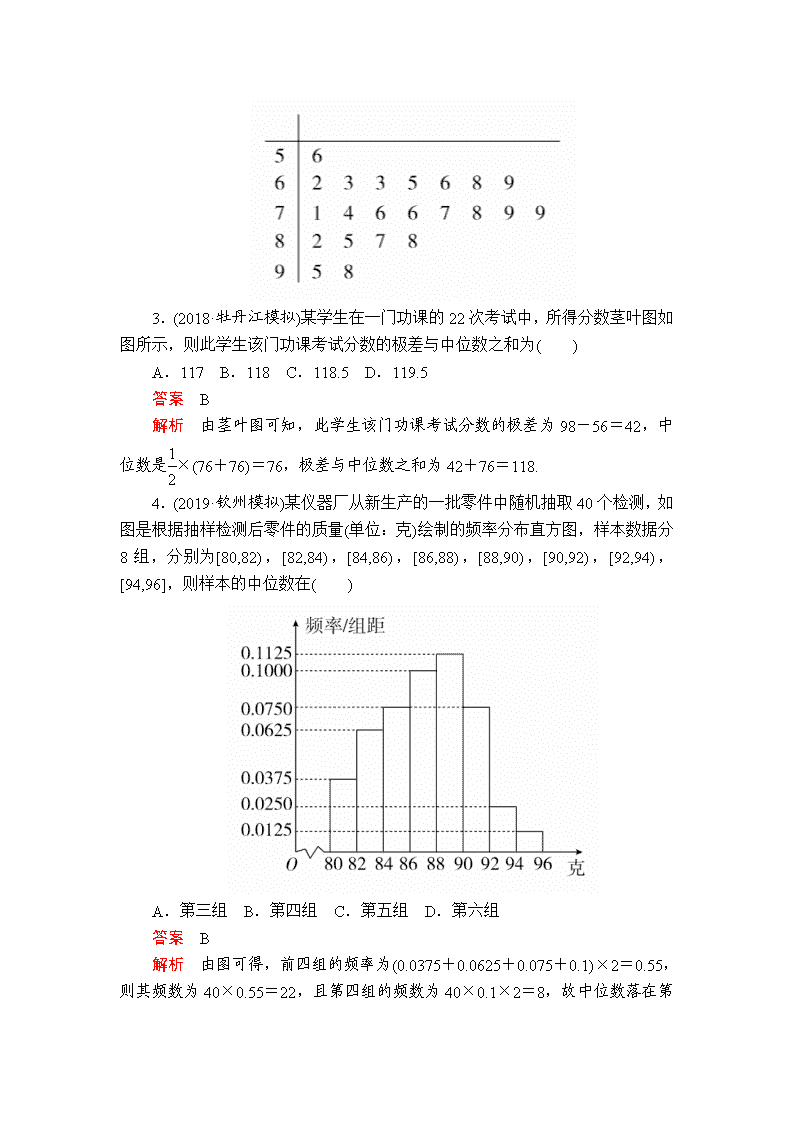
A组　基础关 ‎1．(2018·榆林模拟)一个频数分布表(样本容量为30)不小心被损坏了一部分，只记得样本中数据在[20,60)上的频率为0.8，则估计样本在[40,60)内的数据个数为(　　)‎ A．14 B．‎15 C．16 D．17‎ 答案　B 解析　由频数分布表可知，样本中数据在[20,40)上的频率为＝0.3，又因为样本数据在[20,60)上的频率为0.8，所以样本在[40,60)内的频率为0.8－0.3＝0.5，数据个数为30×0.5＝15.‎ ‎2．甲、乙、丙、丁四人参加国际奥林匹克数学竞赛选拔赛，四人的平均成绩和方差如表：‎ 从这四人中选择一人参加国际奥林匹克数学竞赛，最佳人选是(　　)‎ A．甲 B．乙 C．丙 D．丁 答案　C 解析　丙平均成绩高，方差s2小(稳定)，故最佳人选是丙．‎ ‎3．(2018·牡丹江模拟)某学生在一门功课的22次考试中，所得分数茎叶图如图所示，则此学生该门功课考试分数的极差与中位数之和为(　　)‎ A．117 B．‎118 C．118.5 D．119.5‎ 答案　B 解析　由茎叶图可知，此学生该门功课考试分数的极差为98－56＝42，中位数是×(76＋76)＝76，极差与中位数之和为42＋76＝118.‎ ‎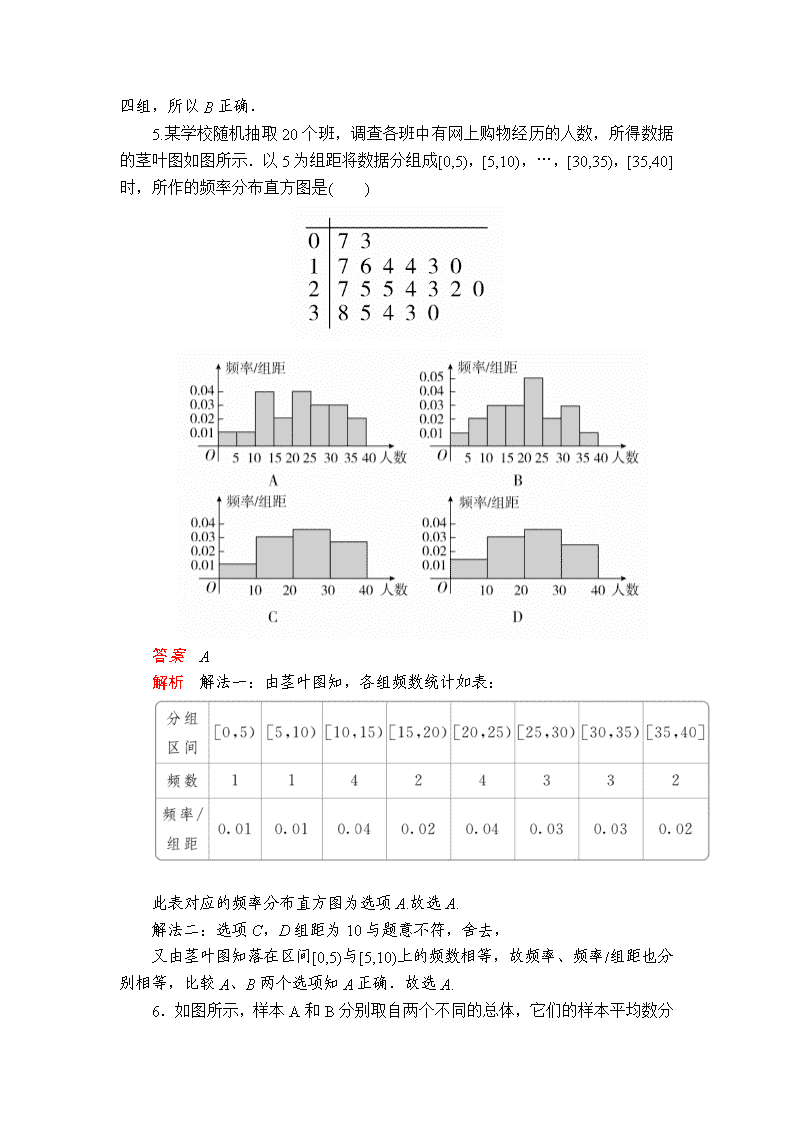4．(2019·钦州模拟)某仪器厂从新生产的一批零件中随机抽取40个检测，如图是根据抽样检测后零件的质量(单位：克)绘制的频率分布直方图，样本数据分8组，分别为[80,82)，[82,84)，[84,86)，[86,88)，[88,90)，[90,92)，[92,94)，[94,96]，则样本的中位数在(　　)‎ A．第三组 B．第四组 C．第五组 D．第六组 答案　B 解析　由图可得，前四组的频率为(0.0375＋0.0625＋0.075＋0.1)×2＝0.55，则其频数为40×0.55＝22，且第四组的频数为40×0.1×2＝8，故中位数落在第四组，所以B正确．‎ ‎5.某学校随机抽取20个班，调查各班中有网上购物经历的人数，所得数据的茎叶图如图所示．以5为组距将数据分组成[0,5)，[5,10)，…，[30,35)，[35,40]时，所作的频率分布直方图是(　　)‎ 答案　A 解析　解法一：由茎叶图知，各组频数统计如表：‎ 此表对应的频率分布直方图为选项A.故选A.‎ 解法二：选项C，D组距为10与题意不符，舍去，‎ 又由茎叶图知落在区间[0,5)与[5,10)上的频数相等，故频率、频率/组距也分别相等，比较A、B两个选项知A正确．故选A.‎ ‎6．如图所示，样本A和B分别取自两个不同的总体，它们的样本平均数分别为A和B，样本标准差分别为sA和sB，则(　　)‎ A.A>B，sA>sB B.AsB C.A>B，sAsB，故选B.‎ ‎7.如图是依据某城市年龄在20岁到45岁的居民上网情况调查而绘制的频率分布直方图，现已知年龄在[30,35)，[35,40)，[40,45]的网民人数成递减的等差数列，则年龄在[35,40)的网民出现的频率为(　　)‎ A．0.04 B．‎0.06 C．0.2 D．0.3‎ 答案　C 解析　由题意得，年龄在[20,25)的网民出现的频率为0.01×5＝0.05，[25,30)的网民出现的频率为0.07×5＝0.35，又[30,35)，[35,40)，[40,45]的网民人数成递减的等差数列，则其频率也成等差数列，又[30,45]的频率为1－0.05－0.35＝0.6，则年龄在[35,40)的网民出现的频率为0.2.‎ ‎8.(2019·长沙模拟)空气质量指数(Air Quality Index，简称AQI)是定量描述空气质量状况的指数，空气质量按照AQI大小分为六级：0～50为优；51～100为良；101～150为轻度污染；151～200为中度污染；201～300为重度污染；大于300为严重污染．一环保人士从当地某年的AQI记录数据中，随机抽取10个，用茎叶图记录如图．根据该统计数据，估计此地该年AQI大于100的天数为________．(该年为365天)‎ 答案　146‎ 解析　该样本中AQI大于100的频数为4，频率为，以此估计此地全年AQI 大于100的频率为，故此地该年AQI大于100的天数约为365×＝146.‎ ‎9．某班有50名学生，一次数学测试平均成绩是92，如果学员为1号到30号学生的平均成绩为90，则学号为31号到50号学生的平均成绩为________．‎ 答案　95‎ 解析　设学号为31号到50号学生的平均成绩为.‎ 由题意得50×92＝30×90＋20，解得＝95.‎ ‎10．从某小区抽取100户居民进行月用电量调查，发现其用电量都在50至350度之间，频率分布直方图如图所示．‎ ‎(1)直方图中x的值为________；‎ ‎(2)在这些用户中，用电量落在区间[100,250)内的户数为________．‎ 答案　(1)0.0044　(2)70‎ 解析　(1)由频率分布直方图知[200,250)小组的频率为1－(0.0024＋0.0036＋0.0060＋0.0024＋0.0012)×50＝0.22，于是x＝＝0.0044.‎ ‎(2)∵数据落在[100,250)内的频率为(0.0036＋0.0060＋0.0044)×50＝0.7，‎ ‎∴所求户数为100×0.7＝70.‎ B组　能力关 ‎1．(2018·西宁一模)某校高二(1)班一次阶段考试数学成绩的茎叶图和频率分布直方图可见部分如图，根据图中的信息，可确定被抽测的人数及分数在[90,100]内的人数分别为(　　)‎ A．20,2 B．24,‎4 C．25,2 D．25,4‎ 答案　C 解析　由频率分布直方图可知，组距为10，[50,60)的频率为0.008×10＝0.08，由茎叶图可知[50,60)的人数为2，设参加本次考试的总人数为N，则N＝＝25，根据频率分布直方图可知[90,100]内的人数与[50,60)的人数一样，都是2.故选C.‎ ‎2．一组数据共有7个数，记得其中有10,2,5,2,4,2，还有一个数没记清，但知道这组数的平均数、中位数、众数依次成等差数列，则这个数的所有可能值的和为(　　)‎ A．－11 B．3‎ C．9 D．17‎ 答案　C 解析　设这个数是x，则平均数为，众数是2.若x≤2，则中位数为2，此时x＝－11；若2s，所以甲、乙两组的整体水平相当，乙组更稳定一些．‎ C组　素养关 ‎　共享单车的出现方便了人们的出行，深受我市居民的喜爱．为调查某校大学生对共享单车的使用情况，从该校8000名学生中按年级用分层抽样的方式随机抽取了100名同学进行调查，得到这100名同学每周使用共享单车的时间(单位：小时)如下表：‎ ‎(1)已知该校大一学生有2400人，求抽取的100名学生中大一学生的人数；‎ ‎(2)作出这些数据的频率分布直方图；‎ ‎(3)估计该校大学生每周使用共享单车的平均时间(同一组中的数据用该组区间的中点值作代表)．‎ 解　(1)设抽取的100名学生中大一学生有x人，则＝，解得x＝30.‎ 所以抽取的100名学生中大一学生有30人．‎ ‎(2)频率分布直方图如图所示．‎ ‎(3)由题意可得＝1×0.050×2＋3×0.200×2＋5×0.125×2＋7×0.100×2＋9×0.025×2＝4.4(小时)．‎ 所以该校大学生每周使用共享单车的平均时间大约为4.4小时．‎