- 2021-05-11 发布 |
- 37.5 KB |
- 17页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级数学上册第15章轴对称图形和等腰三角形15-3等腰三角形(第2课时)课件(新版)沪科版
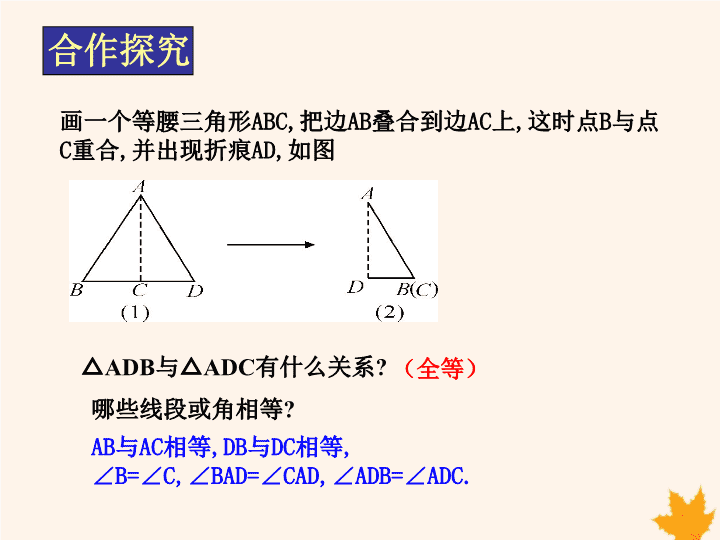
15.3 等腰三角形 第2课时 第十五章 等腰三角形 你知道什么是等腰三角形吗? 画一个等腰三角形ABC,把边AB叠合到边AC上,这时点B与 点C重合,并出现折痕AD,如图 △ADB与△ADC有什么关系? (全等) 哪些线段或角相等? AB与AC相等,DB与DC相等, ∠B=∠C,∠BAD=∠CAD,∠ADB=∠ADC. AD与BC垂直吗? (垂直) 由此你能得出什么结论? 等腰三角形是轴对称图形,底边上的中线所在的直线 是它的对称轴. 讨论:如何证明此结论 已知:如图,△ABC中,AB=AC.求证:∠B=∠C. 证明:取BC的中点D,连接AD.在△ABD 和△ACD中, AB=AC(已知) AD=AD(公共边) BD=CD,(已作) ∴△ABD≌△ACD.(SSS) ∴∠B=∠C.(全等三角形的对应角相等) ∵ 等腰三角形顶角的平分线垂直平分底边, 即等腰三角形顶角的平分线是底边上的中 线也是底边上的高(简称三线合一). 根据性质1,师生共同得到等边三角形的性质:等边 三角形的三个内角都相等,并且每一个角都等于60°. 【例1】 已知:如图所示,在△ABC中,AB=AC, ∠BAC=120°,点D、E是底边上两点,且BD=AD, CE=AE.求∠DAE的度数. 解:∵AB=AC,(已知) ∴∠B=∠C.(等边对等角) ∴∠B=∠C= 1/2×(180°-120°)=30°. 又∵BD=AD,(已知) ∴∠BAD=∠B=30°.(等边对等角) 同理∠CAE=∠C=30°. ∴∠DAE=∠BAC-∠BAD-∠CAE =120°-30°-30° =60° 【例2】已知:如图所示,在△ABC中,AB=AC,点 D在AC上,且BD=BC=AD,求∠A和∠C的度数. 解:∵AB=AC,BD=BC=AD,(已知) ∴∠ABC=∠C=∠BDC, ∠A=∠ABD.(等边对等角) 设∠A=x°, 则∠BDC=∠A+∠ABD=2x°.(三角形的一 个外角等于与它不相邻的两个内角的和) ∵∠ABC=∠C=∠BDC=2x°, ∴x+2x+2x=180.(三角形内角和等于180°) 得x=36. ∴∠A=36°,∠C=72°. 【例3】求证:斜边和一条直角边分别相等的两个 直角三角形全等. 已知,如图所示,在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°, AB=A'B',AC=A'C',求证:Rt△ABC≌Rt△A'B'C' A' B'C' A C B A(A') B B'C(C') 证明:如图所示,在平面内移动Rt△ABC 和Rt△A'B'C',使点A和点A'、点C和点C' 重合,点B和点B'在AC的两侧 ∵∠BCB'=90°+90°=180°,(等式性质) ∴B,C,B'三点在一条直线上。(平角的定义) 在△ABB'中 ∵AB=AB'(已知) ∴∠B=∠B'(等边对等角) 在Rt△ABC和Rt△A'B'C'中, ∵ ∴Rt△ABC≌ Rt△A'B'C'(AAS) A(A') B B'C(C') ∠ACB=∠A'B'C'(已知) ∠B=∠B'(已证) AB=AB'(已知) 1.已知:如图,∠AOB=15°,并且OA=AB=BC=CD. 求证:∠1的度数. 解:∵OA=AB=BC=CD, ∴△OAB、△ABC、△BCD是等腰三角形, ∵∠AOB=15◦,∴∠ABO=15◦, ∴∠CAB=∠AOB+∠ABO=30◦, ∴∠CBD=∠AOB+∠ACB=45◦, ∴∠BCD=90◦, ∴∠1=180◦-30◦-90◦=60◦. 2.已知:如图,AB=AC,AB的垂直平分线ED交AC于点D, ∠A=40°. 求证:∠DBC的度数. 解:∵AB=AC,∠A=40°, ∴∠ABC=70°, ∵ED是线段AB的垂直平分线, ∴∠ABD=∠A=40°, ∴∠DBC=70°- 40°=30°. 3.用一块等腰三角形板,在底边中点做一个记号D;再从顶点悬下 一个铅锤,把这块三角板放在横梁上,看看铅锤线是否通过点D, 就能检查这根横梁是否水平,你知道为什么吗? CB D A 已知:如图,三角形ABC中,AB=AC, D是 BC的中点, (1)求证 AD⊥BC (2)这时BC处于水平位置,为什么? CB D A 用一块等腰三角形板,在底边中点做一个记号D;再从顶点悬 下一个铅锤,把这块三角板放在横梁上,看看铅锤线是否通过点 D,就能检查这根横梁是否水平,你知道为什么吗? ∵AB=AC ,BD=DC ∴ AD⊥BC (等腰三角形三线合一) 等 腰 三 角 形 的 性 质 等边对等角 等腰三角形 三线合一 等边三角形 各角都为60º 1.研究有关等腰三角形的 问题,顶角平分线、底边 中线,底边的高是常用的 辅助线; 2.熟练求解等腰三角形 的顶角、底角的度数; 3.掌握等腰三角形三线合 一的应用。查看更多