北师大版数学九年级上册同步课件-5第五章 复习课

北师大版数学九年级上册同步课件-5第五章 复习课

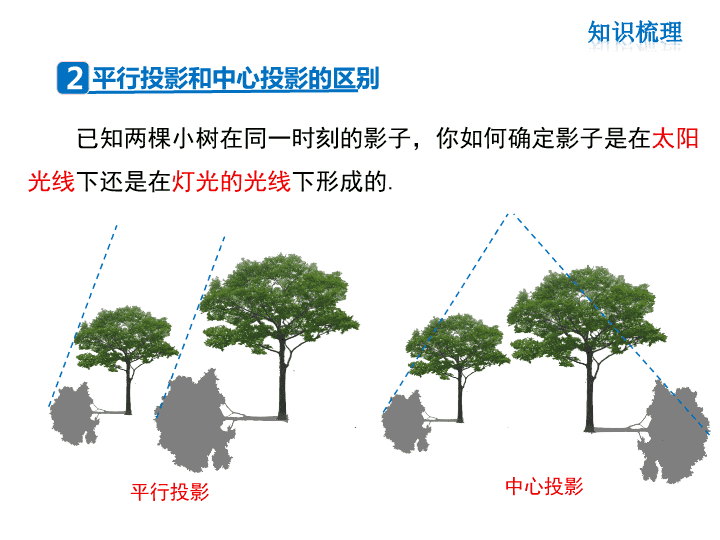
　 第五章 投影与视图 复习课 平行投影和中心投影的定义 由　 形成的投影是平行投影． 由　 形成的投影叫做中心投影． 投影线　 投影面产生的投影叫做正投影． 平行光线 同一点发出的光线 垂直于 【注意】 (1)在实际制图中，经常采用正投影． (2)当物体的某个面平行于投影面时，这个面的正投 影与这个面的形状、大小完全相同． (3)阳光下同一时刻不同物体及影长与光线构成的三 角形相似． 1 已知两棵小树在同一时刻的影子，你如何确定影子是在太阳 光线下还是在灯光的光线下形成的. 平行投影 中心投影 平行投影和中心投影的区别2 视图 三视图是　 、　 、　 的统称． 三视图位置有规定，主视图要在　 ，它的下方应 是　 　，　 　坐落在右边． 三视图的对应规律 主视图和俯视图　 　；主视图和左视图　 　； 左视图和俯视图　 　. 【注意】(1)在画图时，看得见部分的轮廓线通常画成实线， 看不见部分的轮廓线通常画成虚线．(2)画三视图要认真准确， 特别是宽相等． 主视图 俯视图 左视图 左上方 俯视图 左视图 长对正 高平齐 宽相等 3 几何体 主视图 左视图 俯视图 简单几何体的视图 某校墙边有两根木杆． (1)某一时刻甲木杆在阳光下的影子如图所示，你能画出 乙木杆的影子吗？(用线段表示影子) (2)在图中，当乙木杆移动到什么位置时，其影子刚好不 落在墙上？ (3)在你所画的图中有相似三角形吗？为什么？ 平行投影的应用专题1 例1 【解析】所要画出的乙木杆的影子与甲木杆形成的影子是同 一时刻，根据同一时刻两物体的高度比等于其影长的比，同时， 在同一时刻太阳光线是互相平行的，平行移动乙杆，使乙杆顶端 的影长恰好抵达墙角． 解：(1)如图①，过E点作直线DD′的平行线，交AD′所在直 线于E′，则BE′为乙木杆的影子． (2)平移由乙杆、乙杆的影子和太阳光线所构成的图形(即 △BEE′)，直到其影子的顶端E′抵达墙角(如图②)． (3)△ADD′与△BEE′相似．理由略． 由一物体及其影长，画出同一时刻另一物体的影子，其 作法是： (1) 过已知物体的顶端及其影长的端点作一直线，再过另一物 体的顶端作之前所作的直线的平行线，交已知物体的影子所 在直线于一点，则该点到该物体的底部的线段即为影长．但 应注意以下两点：①两物体必须在同一平面内；②所求物体 的影子必须在已知的影子所在的直线上． (2) 在同一时刻，不同物体的底部中点、顶端的中心及影子的 端点所构成的三角形是相似三角形． 练习1: 如图，小明与同学合作利用太阳光线测量旗杆的高度， 身高1.6m的小明落在地面上的影长为BC=2.4m． （1）请你在图中画出旗杆在同一时刻阳光照射下落在地面上 的影子EG； （2）若小明测得此刻旗杆落在地面的影长EG=16m，请求出 旗杆DE的高度. 分析：（1）连结AC，过D点作DG∥AC交BC于G点，则GE 为所求； （2）先证明Rt△ABC∽Rt△DEG，然后利用相似比计算DE 的长. 解答：（1）影子EG如图所示； （2）∵DG∥AC， ∴∠G=∠C， ∴Rt△ABC∽△RtDEG， ∴ ，即 ，解得 ， ∴旗杆的高度为 m． AB BC DE EG  1.6 2.4 16DE  3 2 3 D E  3 2 3 如图，圆桌面（桌面中间有一个直 径为0.4m的圆洞）正上方的灯泡（看作一个 点）发出的光线照射平行于地面的桌面后， 在地面上形成如图所示的圆环形阴影．已知 桌面直径为1.2m，桌面离地面1m，若灯泡离 地面3m，则地面圆环形阴影的面积是（　　） A．0.324πm2 B．0.288πm2 C．1.08πm2 D．0.72πm2 中心投影的应用专题2 例2 解析：如图所示：∵AC⊥OB，BD⊥OB， ∴△AOC∽△BOD， ∴ ，即 ， 解得BD=0.9m. 同理可得：AC′=0.2m，则BD′=0.3m， ∴S圆环形阴影=0.92π﹣0.32π=0.72π（m2）． 故选：D． O A A C O B B D  2 0 . 6 3 B D  练习2: 如图，路灯(P点)距地面8米，身高1.6米的小明从 距路灯的底部(O点)20米的A点，沿OA所在的直线行走14米 到B点时，身影的长度是变长了还是变短了？变长或变短 了多少米？ 解：小明的身影变短了. ∵∠MAC=∠MOP=90°， ∠AMC=∠OMP, ∴△MAC∽△MOP, MA AC= , MO OP  即 MA 1.6 , 20+MA 8  解得MA=5. 同理，由△MAC∽△MOP可得NB=1.5. 所以小明的身影变短了5－1.5=3.5（米）. 如下方左图，是由大小相同的5个小正方体搭成的几何 体，则它的主视图是(　　). 【解析】根据三视图的定义，几何体的主视图应该从前面向 后看，所以本题看到的平面图形应该是选项B，选项A是该几何体 的左视图，选项C是该几何体的俯视图． B 几何体的三视图专题3 例3 总结：根据几何体选择视图，观察几何体时，要正对着几 何体，视线要与放置几何体的平面持平，俯视图反映了物 体的长和宽，主视图反映了物体的长和高，左视图反映了 物体的高和宽． 练习3 下列立体图形中，俯视图是正方形的是（　　） A． B． C． D． B 已知一个几何体的三视图如图所示，则该几何体是(　　) A．棱柱　　B．圆柱 C．圆锥 D．球 【解析】由三个方向看到的平面图形 说出立体图形，首先抓住俯视图，再结合 另两个视图就得出立体图形的名称． 总结：平时要多注意积累常见的几何体的三视图，并进行适 当的分类．如视图可能是圆的有球、圆柱、圆锥等，可能是 三角形的有圆锥、棱锥，可能是长方形的有长方体、圆柱 等． B 根据三视图判断立体图形专题4 例4 练习4:如图，是一个带有方形空洞和 圆形空洞的儿童玩具，如果用下列几 何体作为塞子，那么既可以堵住方形 空洞，又可以堵住圆形空洞的几何体 是（　　） A．　 　B． C． D． 【解析】圆柱从上边看是一个圆，从正面看是一个正方 形，既可以堵住方形空洞，又可以堵住圆形空洞，故选 B． B 由一些大小相同的小正方体组成的几何体三视图如图 所示，那么，组成这个几何体的小正方体的个数是(　　) A．7　　 B．6　　 C．5　　 D．4 由三视图确定立方体的个数专题5 例5 【解析】　由主视图和俯视图可 知，俯视图右边两个方格的位置上各放 置了一个正方体，所以在这两个方格里 分别填入数字1(如图)；由主视图和俯 视图又知，俯视图左边一列上两个方格 每格上最多有2个正方体；又由左视图 和俯视图知，俯视图中左边一列下边一 个方格中应该只有一个正方体，故应填 入数字1，上边应有2个正方体，故填入 数字2.所以组成这个几何体的小正方体 的个数有2＋1＋1＋1＝5(个)． ★由三视图判断组成原几何体的小正方体的块数的一般 解法是： (1)数出主视图各列(竖为列)上正方形的个数，将数字分别填 在俯视图所对应的列中； (2)再数出左视图各列上正方形的个数，将数字分别填在俯视 图所对应的行(横为行)中； (3)在俯视图中的同一个小正方形中，前后两次数字相同的只 取一个数，前后两次数字不同的取较小的数，最后将俯视图 中各小正方形上的数字相加所得结果就是组成原几何体的小 正方体的总块数． 中心投影 投 影 与 视 图 视图 投影 平行投影 圆柱、圆锥、球、直三棱柱、直四棱 柱等简单几何体的三视图