- 2021-02-26 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
五年级下册数学单元测试-第三单元测试卷(A) 人教版(含解析)
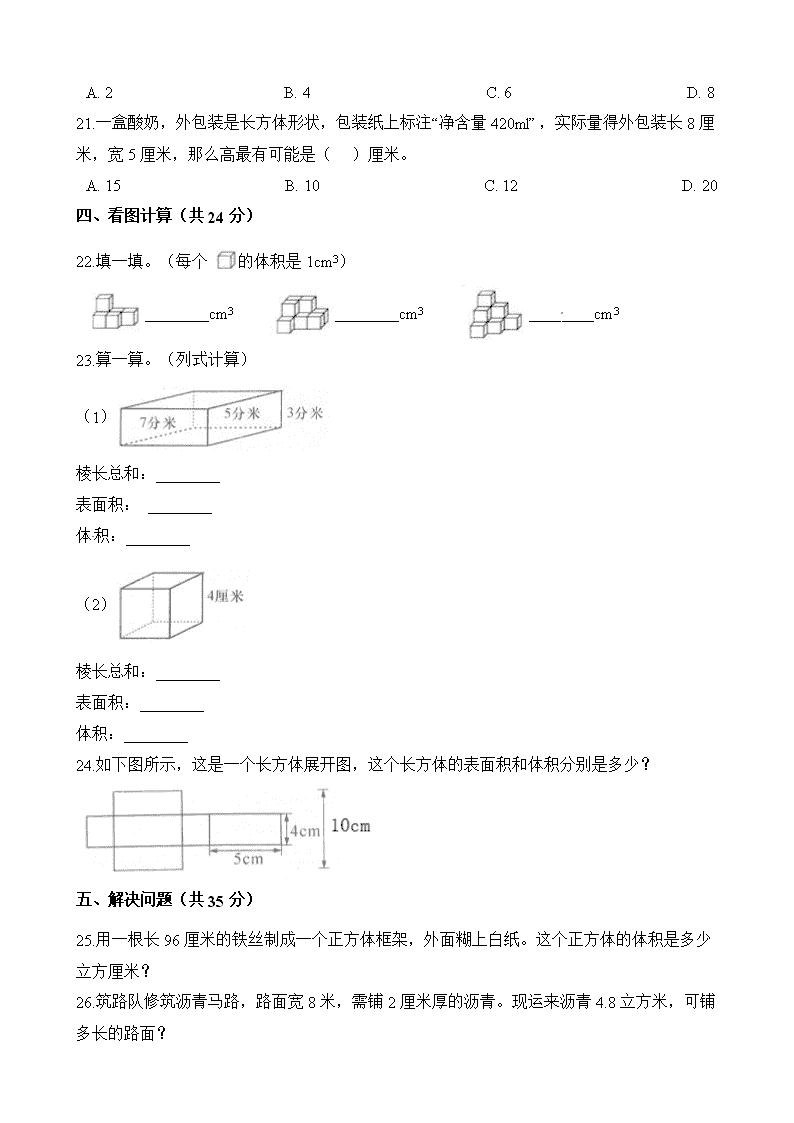
人教版数学2019-2020学年五年级下册第三单元测试卷(A) 一、填空题(每空1分,共30分) 1.在横线上填上合适的单位名称。 我国规定,一次献血一般是200~400________。 一个热水瓶的容积约是2________。 一块橡皮的体积大约是8________。 一本书的体积大约是280________。 2.长方体有________个面,这些面一般都是________形,最多有________个正方形,立方体的________面都是正方形。 3.用棱长1cm的小正方体摆成一个大正方体,至少需要________个这样的小正方体。这个大正方体的表面积是________cm2。 4.2.5立方米=________立方分米 ________立方分米=120立方厘米 ________立方厘米=0.32立方分米 750毫升=________升 0.285L=________mL 0.6dm3=________cm 204m3=________dm3=________cm3 8230cm3=________mL=________L 5.一个正方体的棱长扩大3倍.它的表面积就扩大________倍。 6.一个体积是60dm3的长方体,底面是边长为5dm的正方形,这个长方体的棱长总和是________dm,表面积是________dm2。 7.一个长方体和正方体的楼长总和相等。长方体的长7cm,宽5cm,高3cm,这个正方体的棱长是________cm。 8.从下面的六块铁皮中选五块,焊接成一个无盖水槽(单位:cm)。制作这个水槽需要铁皮________cm2 , 水槽的容积是________cm3。 9.如图:从一张长方形纸剪下一个正方体的展开图,做成一个纸盒。这个纸盒的表面积是________平方厘米。这张长方形纸的面积是________平方厘米。 10.用三个完全相同的立方体拼成一个长方体(如图)后,表面积减少了100dm2 , 原来每个立方体的表面积是________dm2 , 长方体的表面积是________dm2。 二、判断题(共5分) 11.一个棱长是6厘米的正方体,它的表面积和体积相等。( ) 12.一个正方体的棱长总和是24厘米,它的棱长是4厘米。( ) 13.用两个同样大小的正方体拼成的长方体的体积扩大2倍,表面积也扩大到原来的2倍。( ) 14.把一个长方体铁块熔成一个球,它的体积变小了。( ) 15.如果两个长方体的体积相等,它们的长、宽和高也必须相等。( ) 三、选择题(共6分) 16.把一个长方体分割成若干个小正方体,它的体积________,表面积________。 A.不变 B.增加 C.减少 17.下面两个图形分别表示一个长方体的前面和右侧面,那么这个长方体的体积是( )。 A. 12立方厘米 B. 18立方厘米 C. 24立方厘米 D. 36立方厘米 18.把1立方分米的立方体木块切成1立方厘米的小立方体木块,如果把这些小木块排成一行,共有( )厘米。 A. 10 B. 100 C. 1000 D. 10000 19.一个长方体游泳池长25米,宽14米,高2米,它的占地面积是( )。 A. 350平方米 B. 50平方米 C. 28平方米 D. 856平方米 20.把一个棱长4cm的正方体橡皮泥,捏成棱长为2cm的正方体,可以捏( )块。 A. 2 B. 4 C. 6 D. 8 21.一盒酸奶,外包装是长方体形状,包装纸上标注“净含量420ml”,实际量得外包装长8厘米,宽5厘米,那么高最有可能是( )厘米。 A. 15 B. 10 C. 12 D. 20 四、看图计算(共24分) 22.填一填。(每个 的体积是1cm3) ________cm3 ________cm3 ________cm3 23.算一算。(列式计算) (1) 棱长总和:________ 表面积: ________ 体积:________ (2) 棱长总和:________ 表面积:________ 体积:________ 24.如下图所示,这是一个长方体展开图,这个长方体的表面积和体积分别是多少? 五、解决问题(共35分) 25.用一根长96厘米的铁丝制成一个正方体框架,外面糊上白纸。这个正方体的体积是多少立方厘米? 26.筑路队修筑沥青马路,路面宽8米,需铺2厘米厚的沥青。现运来沥青4.8立方米,可铺多长的路面? 27.用两个相同的正方体木块拼成一个长方体,楼长之和减少了24cm。这两个正方体木块原来的棱长之和各是多少厘米? 28.一段长方体钢材长1.5米,横截面的面积是0.25平方分米。这段钢材重多少千克?(1立方分米钢材重7.8千克) 29.一个长方体无盖玻璃鱼缸,长50cm、宽40cm、高30cm。 (1)做这个鱼缸至少需要玻璃多少平方厘米? (2)在鱼缸里注入40L水,水深大约多少厘米? (3)再往水里放入鹅卵石、水草和鱼,测得水面上升了2.5cm,求放入物体的体积一共是多少立方厘米? 30.一个长方体玻璃缸,长12分米,宽10分米,高8分米,水深6.5分米。如果投入一块棱长为6分米的正方体实心铁块,缸里的水溢出多少升? 六、挑战题(附加10分) 31.一个长方体的体积是441立方厘米,如果它的高减少2厘米,它就变成一个正方体。这个正方体的棱长是多少厘米? 32.如图所示是两个长方体容器,如果向这两个容器里注入同样多的水(原来均无水),那么水面高度相差6cm(水均无溢出)甲、乙两个容器里的水面高度分别是多少厘米? 答案解析部分 一、填空题(每空1分,共30分) 1.【答案】 mL;L;cm3;cm3 【考点】体积的认识与体积单位,容积的认识与容积单位 【解析】【解答】解:我国规定,一次献血一般是200~400mL; 一个热水瓶的容积约是2L; 一块橡皮的体积大约是8cm3; 一本书的体积大约是280cm3。 故答案为:mL;L;cm3;cm3。 【分析】根据每种事物的实际情况作答即可。 2.【答案】 6;长方;2;6 【考点】长方体的特征,正方体的特征 【解析】【解答】解:长方体有6个面,这些面一般都是长方形,最多有2个正方形,立方体的6面都是正方形。 故答案为:6;长方;2;6。 【分析】根据长方体和正方体的特征作答即可。 3.【答案】 8;24 【考点】正方体的表面积 【解析】【解答】解:用棱长1cm的小正方体摆成一个大正方体,至少需要8个这样的小正方体。这个大正方体的表面积是2×2×6=24cm2。 故答案为:8;24。 【分析】用一个小正方体摆成一个较大的正方体,这个正方体的每条棱都是由2个正方体拼成的,所以这个大正方体的表面积=(小正方体的棱长×2)2×6。 4.【答案】 2500;0.12;320;0.75;285;600;204000;204000000;8230;8.23 【考点】含小数的单位换算,体积单位间的进率及换算,容积单位间的进率及换算,体积和容积的关系 【解析】【解答】解:2.5立方米=2500立方分米;0.12立方分米=120立方厘米; 320立方厘米=0.32立方分米;750毫升=0.75升; 0.285L=285mL;0.6dm3=600cm; 204m3=204000dm3=204000000cm3; 8230cm3=8230mL=8.23L。 故答案为:2500;0.12;320;0.75;285;600;204000;204000000;8230;8.23。 【分析】1立方米=1000立方分米=1立方厘米;1立方分米=1000立方厘米; 1立方分米=1升;1毫升=1立方厘米;1升=1000毫升; 高级单位化低级单位乘进率;低级单位化高级单位除以进率。 5.【答案】 9 【考点】正方体的表面积 【解析】【解答】解:它的表面积就扩大3×3=9倍。 故答案为:9。 【分析】正方体的表面积=棱长×棱长×6,当棱长扩大3倍时,现在正方体的表面积=(棱长×3)×(棱长×3)×6=棱长×棱长×6×9=原来正方体的表面积×9。 6.【答案】 49.6;98 【考点】长方体的特征,长方体的表面积 【解析】【解答】解:60÷(5×5)=2.4dm,(2.4+5+5)×4=49.6dm,所以这个长方体的棱长总和是49.6dm;2.4×5×4+5×5×2=98dm2 , 所以表面积是98dm2。 故答案为:49.6;98。 【分析】长方体的高=长方体的体积÷底面积,所以长方体的棱长总和=(长+宽+高)×4,长方体的表面积=长×宽×2+长×高×2+宽×高×2。 7.【答案】 5 【考点】长方体的特征,正方体的特征 【解析】【解答】解:(7+5+3)×4÷12=15×4÷12=5cm,所以正方体的棱长是5cm。 故答案为:5。 【分析】长方体的棱长总和=(长+宽+高)×4,正方体的棱长=正方体的棱长总和÷12。 8.【答案】 470;900 【考点】长方体的表面积,长方体、正方体的容积 【解析】【解答】解:选1块 ,2块 ,2块 ,这个水槽表面积:9×20+(5×9+5×20)×2=470(cm2),水槽容积:9×20×5=900(cm3)。 故答案为:470;900。 【分析】根据长方体的特征选择合适的铁片即可; 水槽的表面积=长×宽+长×高×2+宽×高×2; 水槽容积=长×宽×高。 9.【答案】 150;300 【考点】长方形的面积,正方体的表面积 【解析】【解答】解:正方体棱长:20÷4=5(厘米),这个纸盒表面积:5×5×6=150(cm2),长方形的宽:5×3=15(cm),所以长方形的面积是20×15=300(cm2)。 故答案为:150;300。 【分析】从图中可以看出,长方形纸的长可以分成4个小正方形,所以拼成的正方体的棱长=长方形纸的长÷4,故这个纸盒表面积=正方体的棱长×正方体的棱长×6; 长方形的宽=正方体的棱长÷长方形纸的宽可以分成小正方形的个数,所以长方形的面积=长×宽。 10.【答案】 150;350 【考点】长方体的表面积,正方体的表面积 【解析】【解答】解:100÷4=25dm2 , 25×6=150dm2 , 所以原来每个立方体的表面积是150dm2;150×3-100=350dm2 , 所以长方体的表面积是350dm2。 故答案为:150;350。 【分析】用三个完全相同的立方体拼成一个长方体,就会减少4个正方形面,那么每个正方形面的面积=减少的表面积÷4,所以原来每个立方体的表面积=每个正方形面的面积×6;长方体的表面积=原来每个立方体的表面积×3-减少的表面积。 二、判断题(共5分) 11.【答案】 错误 【考点】正方体的表面积,正方体的体积 【解析】【解答】解:一个棱长是6厘米的正方体,它的表面积=6×6×6=216(平方厘米),它的体积=6×6×6=216(立方厘米),虽然数值相同,但单位不同,所以它的表面积和它的体积不相等,故“一个棱长是6厘米的正方体,它的表面积和体积相等”这个说法是错误的。 故答案为:错误。 【分析】正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,据此代入数据解答即可,注意:单位不同则不相等。 12.【答案】 错误 【考点】正方体的特征 【解析】【解答】解:24÷12=2厘米,所以它的棱长是2厘米。 故答案为:错误。 【分析】正方体的棱长=正方体的棱长之和÷12,据此作答即可。 13.【答案】 错误 【考点】长方体的表面积,正方体的表面积,长方体的体积,正方体的体积 【解析】【解答】解:用两个同样大小的正方体拼成的长方体的体积扩大2倍,但是表面积不一定也扩大到原来的2倍。 故答案为:错误。 【分析】用两个同样大小的正方体拼成的长方体,这个长方体的体积是这两个正方体的体积之和,也就是说是正方体的体积的2倍;但是表面积比原来减少了2个正方体的面,所以表面积没有扩大到原来的2倍。 14.【答案】 错误 【考点】体积的等积变形 【解析】【解答】解:把一个长方体铁块熔成一个球,它的体积不变。 故答案为:错误。 【分析】因为长方体铁块熔成一个球之后,还是原来的东西,所以体积不变。 15.【答案】 错误 【考点】长方体的体积 【解析】【解答】解:如果两个长方体的体积相等,它们的长、宽和高不一定相等。 故答案为:错误。 【分析】当其中一个长方体的长、宽、高分别是6,4,2时,它的面积是6×4×2=48;当另一个长方体的长、宽、高分别是4、3、4时,它的面积是4×3×4=48。这两个长方体的体积相等,但是它们的长、宽和高不相等。 三、选择题(共6分) 16.【答案】 A;B 【考点】长方体的表面积,正方体的表面积,长方体的体积,正方体的体积 【解析】【解答】解:把一个长方体分割成若干个小正方体,它的体积不变,表面积增加。 故答案为:A;B。 【分析】长方体分割成若干个小正方体,还是原来的东西,所以体积不变,而每切一刀都会增加2个面。 17.【答案】 D 【考点】长方体的体积 【解析】【解答】解:6×3×2=36立方厘米,所以这个长方体的体积是36立方厘米。 故答案为:D。 【分析】长方体从前面看,可以得到长方体的长和高,从左侧面看是宽和高,所以长方体的体积=长×宽×高。 18.【答案】 C 【考点】立方体的切拼 【解析】【解答】解:10×10×10=1000,所以共有1000厘米。 故答案为:C。 【分析】1分米=10厘米,1立方分米的立方体木块每条棱可以切的块数,那么一共可以切成的块数=这些木块排成一行的长度=1立方分米的立方体木块每条棱可以切的块数×1立方分米的立方体木块每条棱可以切的块数×1立方分米的立方体木块每条棱可以切的块数。 19.【答案】 A 【考点】长方形的面积 【解析】【解答】解:25×14=350平方米,所以它的占地面积是350平方米。 故答案为:A。 【分析】游泳池的占地面积=游泳池的长×游泳池的宽,据此代入数据作答即可。 20.【答案】 D 【考点】正方体的体积 【解析】【解答】解:4×4×4=64cm3 , 2×2×2=8cm3 , 64÷8=8块,所以可以捏8块。 故答案为:D。 【分析】可以捏的块数=棱长是4cm的正方体的橡皮泥的体积÷棱长是2cm的正方体的橡皮泥的体积,其中正方体的体积=棱长×棱长×棱长。 21.【答案】 C 【考点】长方体、正方体的容积 【解析】【解答】解:420ml=420cm2 , 420÷8÷5=10.5cm,所以高最有可能是12厘米。 故答案为:C。 【分析】净含量是指盒子内酸奶的体积; 酸奶的高=净含量÷长÷宽,因为盒子的高要大于酸奶的高,所以取合适的高即可。 四、看图计算(共24分) 22.【答案】 6;10;10 【考点】组合体的体积的巧算 【解析】【解答】解:①由图可知:共有1×2+4=6个小正方体,所以立体图形的体积是6×1=6(cm3); ②由图可知:共有3×2+4=10个小正方体,所以立体图形的体积是10×1=10(cm3); ③由图可知:共有1×3+2×2+3=10个小正方体,所以立体图形的体积是10×1=10(cm3)。 故答案为:6;10;10。 【分析】先确定小正方体的个数,再根据“立体图形的体积=小正方体的个数×每个小正方体的体积”计算出每个立方图形的体积。 23.【答案】 (1)(7+5+3)×4=60(分米);(7×5+5×3+7×3)×2=142(平方分米);7×5×3=105(立方分米) (2)4×12=48(厘米);4×4×6=96(平方厘米);4×4×4=64(立方厘米) 【考点】长方体的特征,正方体的特征,长方体的表面积,正方体的表面积,长方体的体积,正方体的体积 【解析】【分析】(1)长方体的棱长总和=(长+宽+高)×4; 长方体的表面积=(长×宽+长×高+宽×高)×2; 长方体的体积=长×宽×高; (2)正方体的棱长总和=棱长×12; 正方体的表面积=棱长×棱长×6; 正方体的体积=棱长×棱长×棱长。 24.【答案】 解:(10-4)÷2=3(cm) 表面积:(5×4+5×3+4×3)×2=94(cm2) 体积:5×4×3=60(cm3) 【考点】长方体的表面积,长方体的体积 【解析】【分析】从图中可以看出,长方体的高=(10-宽)÷2,所以 长方体的表面积=(长×宽+长×高+宽×高)×2;长方体的体积=长×宽×高。 五、解决问题(共35分) 25.【答案】 解:96÷12=8(厘米) 8×8×8=512(立方厘米) 答:这个正方体的体积是512立方厘米。 【考点】正方体的特征,正方体的体积 【解析】【分析】正方体的棱长=正方体的棱长总和÷12,所以正方体的体积=棱长×棱长×棱长。 26.【答案】 解:2厘米=0.02米 4.8÷(8×0.02)=30(米) 答:可铺30米长的路面。 【考点】长方体的体积 【解析】【分析】先把单位进行换算,即2厘米=0.02米,所以可以铺的长度=沥青的体积÷(路面的宽÷路面的高),据此代入数据作答即可。 27.【答案】 解:24÷8×12=36(cm) 答:这两个正方体木块原来的棱长之和各是36厘米。 【考点】正方体的特征 【解析】【分析】两个正方体拼成一个长方体,棱长少了两个面,一个面有4条棱长即少了8条棱长,所以原正方体的棱长=棱长之和÷减少的棱长的个数,所以这两个正方体木块原来的棱长之和=原正方体的棱长×12。 28.【答案】 解:1.5米=15分米 15×0.25×7.8=29.25(千克) 答:这段钢材重29.25千克。 【考点】长方体的体积 【解析】【分析】先把单位进行换算,即1.5米=15分米,所以这段钢材的重量=钢材的体积×1立方分米钢材的重量,其中钢材的体积=钢材的长×钢材的横截面面积,据此代入数据作答即可。 29.【答案】 (1)解:50×40+2×30×40+2×50×30=7400(cm2) 答:做这个鱼缸至少需要玻璃7400cm2。 (2)解:40L=40000cm3 40000÷(50×40)=20(cm) 答:水深大约20cm。 (3)解:2.5×50×40=5000(cm2) 答:放入物体的体积一共是5000cm3。 【考点】长方体的表面积,不规则物体的体积算法,长方体、正方体的容积 【解析】【分析】(1)做这个鱼缸至少需要玻璃的平方厘米数=长×宽+长×高×2+宽×高×2,据此代入数据作答即可; (2)先进行单位换算,40L=40000cm3 , 那么水的深度=注入水的体积÷(长×宽),据此代入数据作答即可; (3)放入物体的体积=长×宽×水面上升的距离,据此代入数据作答即可。 30.【答案】 解:6.6×6×6=216(立方分米) 12×10×(8-6.5)=180(立方分米) 216-180=36(升) 答:缸里的水溢出36升。 【考点】长方体的体积 【解析】【分析】缸里的水溢出溢出的体积=正方体实心铁块的体积-玻璃缸中还可以放入水的体积,其中正方体实心铁块的体积=棱长×棱长×棱长,玻璃缸中还可以放入水的体积=长×宽×(高-水的深度),据此代入数据作答即可。 六、挑战题(附加10分) 31.【答案】 解:441=3×3×7×7=7×7×9, 9-2=7(厘米) 答:正方体的棱长是7厘米。 【考点】分解质因数 【解析】【分析】长方体的高减少2厘米后是正方体,所以长方体的长和宽相等,而长方体的体积=长×宽×高,所以可以先把长方体的体积分解质因数,只需要有两个数值相等,另一个数值比这两个值小2,那么相等的这个数值就是正方体的棱长。 32.【答案】 解:设乙容器水面高度为x厘米,甲容器水面高度为(x+6)厘米,则(6×6)x=(4×4)(x+6),解得x=4.8,甲容器水面高度:x+6=4.8+6=10.8(厘米) 答:乙容器水面高度是4.8厘米,甲容器水面高度是10.8厘米。 【考点】长方体的体积,列方程解含有多个未知数的应用题 【解析】【分析】此题关键是注入水一样多即体积一样大,根据高度之间的关系和已知的底面积可分别求出两容器水面高度。查看更多