八年级上数学课件八年级上册数学课件《一次函数的图像与性质》 北师大版 (7)_北师大版

八年级上数学课件八年级上册数学课件《一次函数的图像与性质》 北师大版 (7)_北师大版

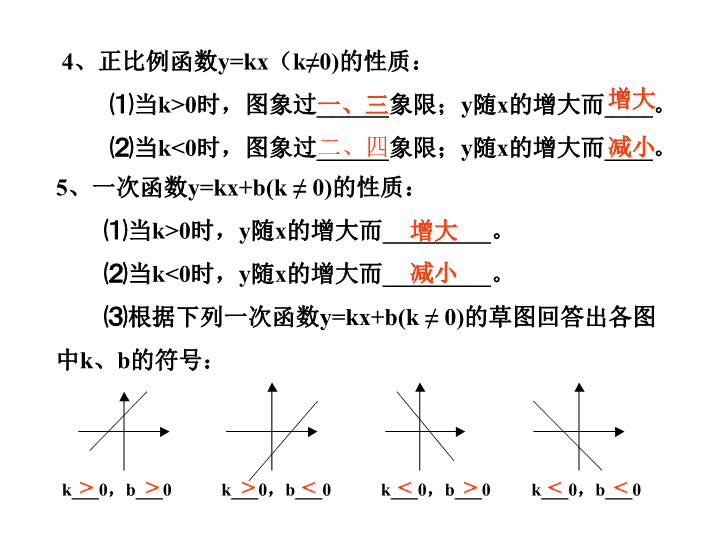
知识要点： 　　1、一次函数的概念：函数y=_______(k、b为常 数，k______)叫做一次函数。当b_____时，函数 y=____(k____)叫做正比例函数。 kx ＋b ≠０ = ０ ≠０kx ★理解一次函数概念应注意下面两点： 　　⑴、解析式中自变量x的次数是___次， ⑵、比例系数_____。 1 K≠0 　　2、正比例函数y=kx(k≠0)的图象是过点（_____） 的 　　 3、一次函数y=kx+b(k≠0)的图象是过点（0，_ __),（____，0)的__________。 0，0 一条直线 b 一条直线 b k  4、正比例函数y=kx（k≠0)的性质： 　　⑴当k>0时，图象过______象限；y随x的增大而____。 　　⑵当k<0时，图象过______象限；y随x的增大而____。 一、三 增大 二、四 减小 5、一次函数y=kx+b(k ≠ 0)的性质： 　　⑴当k>0时，y随x的增大而_________。 　　⑵当k<0时，y随x的增大而_________。 　　⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图 中k、b的符号： 增大 减小 k___0，b___0 k___0，b___0 k___0，b___0 k___0，b___0< < > < <>>> 一 次 函 数正 比 例 函 数 解析式 图 象 性 质 y = k x ( k≠0 ) ｙ=k x + b（k,b为常数，且k ≠0） k>0　 k<0 k>0　 k<0 y xo y xo x y o y xo k>0,b>0 k>0,b<0 k<0,b>0 k<0,b<0 y xo x y o k>0时,在一三象限; k<0时,在二四象限. 正比例函数是特殊的一次函数 k>0,b>0时在一二三象限; k>0,b<0时在一三四象限 k<0, b>0时,在一二四象限. k<0, b<0时,在二三四象限 当k>0时,y随x的增大而增大; 当k<0时,y随x的增大而减小. lkl越大，直线越陡。 k1=k2,两直线平行；k1≠k2,两直线相交；k1k2=-1,两直线互相垂直。 例1、已知 ①y是x一次函数。 则当m、n满足什么条件时： ②y是x正比例函数。 3)2( 32   nxmy m 例2　填空题： (1)　有下列函数：①　　　　　 , ②　y=-x　　　 , ③　　　 , ④ 。其中过原点的直 线是_____；函数y随x的增大而增大的是___________； 函数y随x的增大而减小的是_ _____；图象过第一、二、 三象限的是_____。 56  xy 4 xy 34  xy ② ①、③ ③ 　　(2)、如果一次函数y=kx-3k+6的图象经过原点，那么 k的值为________。 　　(3)、已知y-1与x成正比例，且x=－2时，y=4，那么y与 x之间的函数关系式为_________________。3 12y x   k=2 ④② 解：（1）由题意: 2=﹣(m+1）+2m ﹣6解得 m = 9 ∴ y = 10x+12 (2) 由题意，m +1= 2 解得 m = 1 ∴ y = 2x﹣4 解：设一次函数解析式为y=kx+b， 把x=1时， y=5；x=6时，y=0代入解析式，得      06 5 bk bk 解得      6 1 b k ∴一次函数的解析式为　y= - x+6。 点评：用待定系数法求一次函数y=kx+b的解析式，可由已知 条件给出的两对x、y的值，列出关于k、b的关系式。由此求 出k、b的值，就可以得到所求的一次函数的解析式。 例4、已知一次函数y=kx+b(k≠0)在x=1时，y=5，且 它的图象与x轴交点的横坐标是６，求这个一次函数的 解析式。