- 2021-05-10 发布 |
- 37.5 KB |
- 22页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级上数学课件- 13-1-1 等腰三角形 课件( 22张PPT)_人教新课标
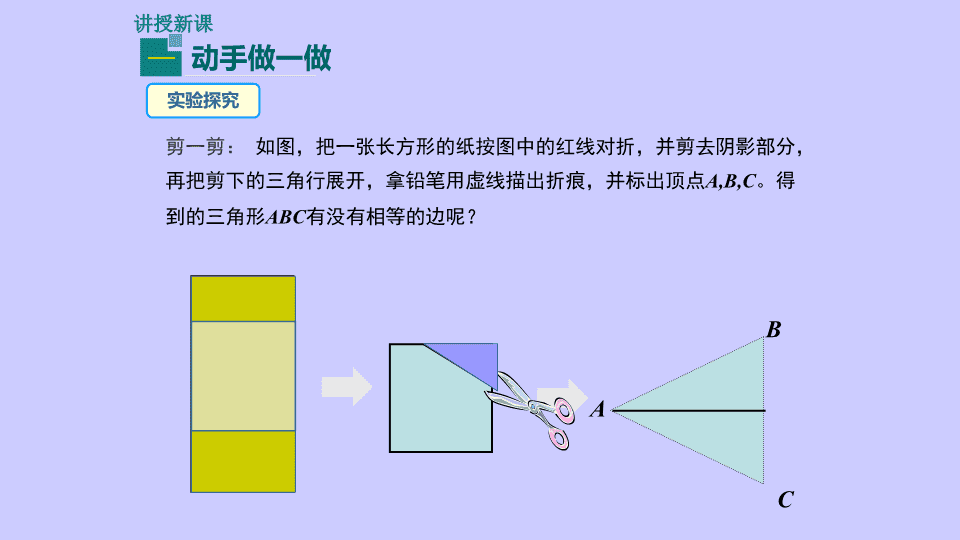
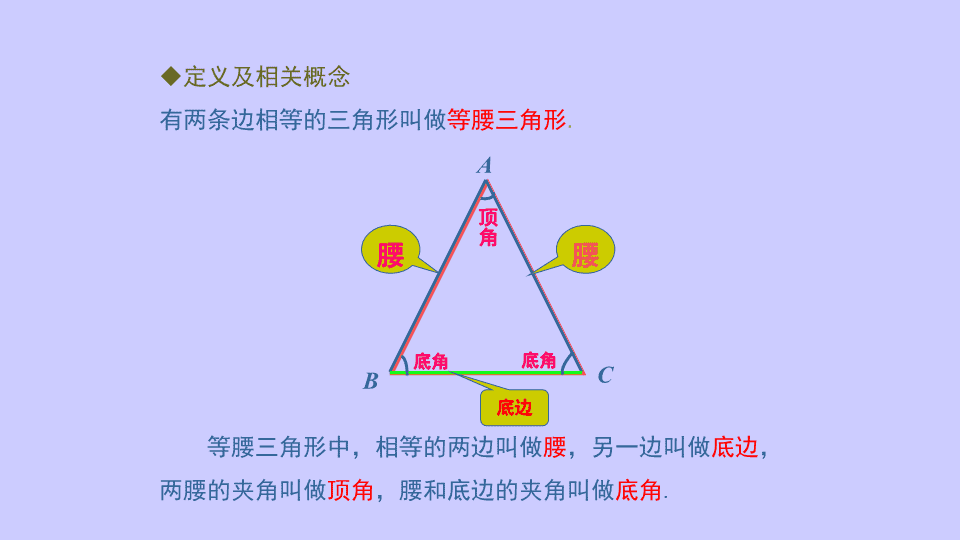
讲授新课 动手做一做一 实验探究 剪一剪: 如图,把一张长方形的纸按图中的红线对折,并剪去阴影部分, 再把剪下的三角行展开,拿铅笔用虚线描出折痕,并标出顶点A,B,C。得 到的三角形ABC有没有相等的边呢? A B C u定义及相关概念 有两条边相等的三角形叫做等腰三角形. 等腰三角形中,相等的两边叫做腰,另一边叫做底边, 两腰的夹角叫做顶角,腰和底边的夹角叫做底角. A CB 腰腰 底边 顶 角 底角底角 把剪出的等腰三角形ABC沿折痕对折, 请同学们小组讨论一下,找出其中重合的线 段和角.说说哪些线段相等,哪些角相等。 重合的线段 重合的角 A C B D AB=AC BD=CD AD=AD ∠B = ∠C ∠BAD = ∠CAD ∠ADB = ∠ADC 想一想 擦去那条折痕,等腰三角形的两个底角相等 吗?你能发现等腰三角形的性质吗?说说你的 猜想。 猜想与论证一: 等腰三角形的两个底角相等。 分析:1.如何证明两个角相等? 2.如何构造两个全等的三角形? 性质1 A B C 同学们,为了便于证明,可以把 这个猜想改成“如果......那么......” 的形式吗? 性质1 等腰三角形的两个底角相等(等边对等角). A B CD 猜想与验证 已知:△ABC 中,AB=AC, 求证:∠B=∠C . 证法1:证明:作底边BC边上的中线AD. 在△ABD与△ACD中: AB=AC(已知), BD=CD(作图), AD=AD(公共边), ∴△ABD≌△ACD(SSS). ∴∠B=∠C(全等三角形对应角相等). 应用格式: ∵AB=AC(已知) ∴∠B=∠C(等边对等角) 证法欣赏 证法2:作顶角∠BAC的平分线AD, 交BC于点D. ∵AD平分∠BAC , ∴∠1=∠2. 在△ABD与△ACD中, AB=AC(已知), ∠1=∠2(已证), AD=AD(公共边), ∴ △ABD ≌ △ACD(SAS), ∴ ∠B=∠C. A B CD ( ( 1 2 应用格式: ∵AB=AC(已知) ∴∠B=∠C(等边对等角) 证法3:作底边BC的高AD,交BC于点D. ∵AD⊥BC, ∴ ∠ADB =∠ADC=90°. 在Rt△ABD与Rt△ACD中, AB=AC(已知), AD=AD(公共边), ∴ Rt△ABD ≌ Rt△ACD(HL), ∴ ∠B=∠C. 证法欣赏 A B CD 应用格式: ∵AB=AC(已知) ∴∠B=∠C(等边对等 角) A A B ┌ 作△ABC的高AD. D C B C 等腰三角形常见辅助线 1 作顶角的平分线AD. D 2 A B C 作△ABC底边BC的 中线AD. D •请同学们现在思考并做一下书上77页练习题 第一题 大家想一想,通过刚才的三种证 明方法,顶角的平分线,底边上的 中线,底边上的高有什么关系呢? 猜想与论证二: A B C D ???,还有呢 你会证明吗? 等腰三角形性质 性质2 等腰三角形的顶角平分线、底边 上的中线、底边上的高互相重合。 (可简记为“三线合一”) 注意:是指顶角的平分线,底边上的高和中线才有这一性质.而 腰上高和中线与底角的平分线不具有这一性质. 性质2:在△ABC中, ( 1 ) ∵ AB=AC AD是角平分线, ∴ ⊥ , ____=_____ ; ( 2 ) ∵ AB=AC AD是中线, ∴ ⊥ ,∴∠ = ∠____; ( 3 ) ∵ AB=AC AD⊥BC, ∴∠_____=∠______,_____=______ 。BAD CAD BAD CAD AD BC AD BC BD CD BD CD 数学语言 •请同学们做一下书上第77页练习题第2题 A B C D 例1 如图,在△ABC中 ,AB=AC,点D在AC上,且 BD=BC=AD,求△ABC各角的度数. 三、典例精析 (1)找出图中所有相等的角;(等边对等角) (2)指出图中有几个等腰三角形? ∠A=∠ABD, ∠C=∠BDC=∠ABC; △ABC, △ABD, △BCD. A B C D x ⌒ 2x⌒ 2x ⌒ ⌒ 2x 例1 如图,在△ABC中 ,AB=AC,点D在AC上,且 BD=BC=AD,求△ABC各角的度数. 典例精析 (3)观察∠BDC与∠A、∠ABD的关系, ∠BDC与∠ABC、∠C的关系呢? ∠BDC= ∠A+ ∠ABD=2 ∠A=2 ∠ABD, ∠BDC=∠C=∠ABC= 2 ∠A, (4)设∠A=x,请把△ ABC的内角和用含 x的式子表示出来. ∵ ∠A+ ∠ABC+ ∠ C=180 ° ∴x+2x+2x=180 °, A B C D 解:∵AB=AC,BD=BC=AD, ∴∠ABC=∠C=∠BDC, ∠A=∠ABD. 设∠A=x,则∠BDC= ∠A+ ∠ABD=2x, 从而∠ABC= ∠C= ∠BDC=2x, 于是在△ABC中,有 ∠A+∠ABC+∠C=x+2x+2x=180 ° , 解得x=36 ° ,在△ABC中, ∠A=36°, ∠ABC=∠C=72°. x ⌒ 2x⌒ 2x ⌒ ⌒ 2x 例1 如图,在△ABC中 ,AB=AC,点D在AC上,且 BD=BC=AD,求△ABC各角的度数. 典例精析 请同学们做下书上第77页的练习题 第3题 等腰三角形是轴对称图形,对称轴是什么? A B P l • 四、作业布置 书上81页复习巩固第1、2、4题做在作业本上 A CB D 如图,是西安半坡博物馆屋顶的截面图,已经知道它的两边AB 和AC是相等的.建筑工人师傅对这个建筑物做出了两个判断: ①工人师傅在测量了∠B为37°以后,并没有测量∠C ,就说 ∠C 的度数也是37°;②工人师傅要加固屋顶,他们通过测量找 到了横梁BC的中点D,然后在AD两点之间钉上一根木桩,他们 认为木桩是垂直横梁的. 请同学们想想,工人师傅的说法对吗?请说明理由. 下课了!查看更多