九年级数学上册第一章特殊平行四边形3正方形的性质与判定第1课时正方形的性质作业课件新版北师大版

九年级数学上册第一章特殊平行四边形3正方形的性质与判定第1课时正方形的性质作业课件新版北师大版

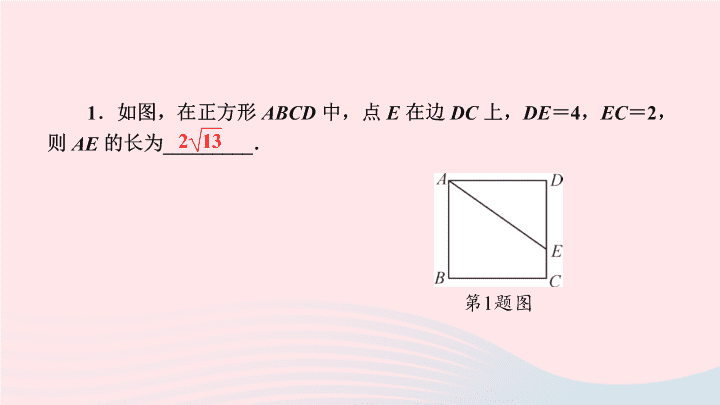
第一章　特殊平行四边形 1.3　正方形的性质与判定 第1课时　正方形的性质 3 ． (2019 · 凉山州 ) 如图，正方形 ABCD 的对角线 AC ， BD 相交于点 O ， E 是 OC 上一点，连接 EB . 过点 A 作 AM ⊥ BE ，垂足为 M ， AM 与 BD 相交于点 F . 求证： OE ＝ OF . 证明：∵四边形 ABCD 是正方形．∴∠ BOE ＝∠ AOF ＝ 90° ， OB ＝ OA . 又∵ AM ⊥ BE ，∴∠ MEA ＋∠ MAE ＝ 90° ＝∠ AFO ＋∠ MAE ，∴∠ MEA ＝∠ AFO .∴△ BOE ≌△ AOF (AAS).∴ OE ＝ OF 4 ． (2019 · 鄂尔多斯 ) 如图，在正方形 ABCD 的外侧，作等边△ ABE ，则∠ BED 的度数为 ( ) A ． 15° B ． 35° C ． 45° D ． 55° C 5 ．如图，已知 P 是正方形 ABCD 对角线 BD 上一点，且 BP ＝ BC ，则∠ ACP 的度数是 ( ) A ． 45° B ． 22.5° C ． 67.5° D ． 75° B 6 ． ( 教材习题 1.7 第 2 题变式题 ) 如图，四边形 ABCD 是正方形，△ EBC 是等边三角形． (1) 求证：△ ABE ≌△ DCE ； (2) 求∠ AED 的度数． B 8 ． (2019 · 湘西州 ) 如图，在正方形 ABCD 中，点 E ， F 分别在边 CD ， AD 上，且 AF ＝ CE . (1) 求证：△ ABF ≌△ CBE ； (2) 若 AB ＝ 4 ， AF ＝ 1 ，求四边形 BEDF 的面积． 9 ． (2019 · 绍兴 ) 如图，正方形 ABCD 的边 AB 上有一动点 E ，以 EC 为边作矩形 ECFG ，且边 FG 过点 D . 在点 E 从点 A 移动到点 B 的过程中，矩形 ECFG 的面积 ( ) A ．先变大后变小 B ．先变小后变大 C ．一直变大 D ．保持不变 D ①②③ 12 ． (2019 · 内江 ) 如图，在正方形 ABCD 中，点 E 是 BC 上的一点，点 F 是 CD 延长线上的一点，且 BE ＝ DF ，连接 AE ， AF ， EF . (1) 求证：△ ABE ≌△ ADF ； (2) 若 AE ＝ 5 ，请求出 EF 的长． 13 ．如图，四边形 ABCD 和四边形 DEFG 都是正方形，点 E ， G 分别在 AD ， CD 上，连接 AF ， BF ， CF . (1) 求证： AF ＝ CF ； (2) 若∠ BAF ＝ 35° ，求∠ BFC 的度数． (1) 证明：∵四边形 ABCD 和四边形 DEFG 都是正方形，∴∠ DEF ＝∠ DGF ＝ 90° ， AD ＝ CD ， ED ＝ GD ， FE ＝ FG ，∴∠ AEF ＝∠ CGF ＝ 90° ， AD － ED ＝ CD － GD ，即 AE ＝ CG . 在△ AEF 和△ CGF 中，∵ AE ＝ CG ，∠ AEF ＝∠ CGF ＝ 90° ， FE ＝ FG ，∴△ AEF ≌△ CGF (SAS) ，∴ AF ＝ CF 　 (2)∠ BFC ＝ 100° 14 ．如图，四边形 ABCD 是边长为 a 的正方形，点 G ， E 分别是边 AB ， BC 的中点，∠ AEF ＝ 90° ，且 EF 交正方形外角∠ DCH 的平分线 CF 于点 F . (1) 求证：∠ BAE ＝∠ FEC ； (2) 求证：△ AGE ≌△ ECF ； (3) 求△ AEF 的面积． 解： (1)∵∠ AEF ＝ 90° ，∴∠ FEC ＋∠ AEB ＝ 90°. 在 Rt△ ABE 中，∠ AEB ＋∠ BAE ＝ 90° ，∴∠ BAE ＝∠ FEC