- 2021-05-10 发布 |
- 37.5 KB |
- 182页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学压轴题精选精析
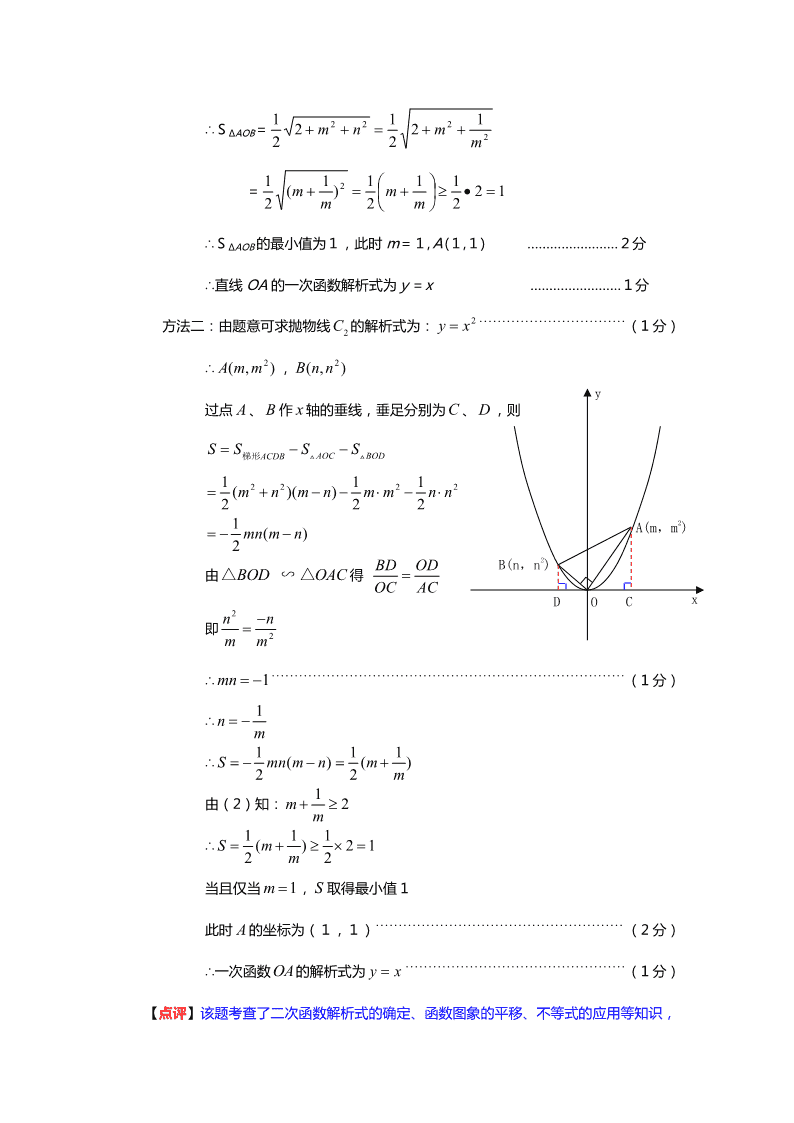
2012 年各地中考数学压轴题精选精析 (1.2012 黄石) 25.(本小题满分 10 分)已知抛物线 1C 的函数解析式为 2 3 ( 0)y ax bx a b ,若抛物线 1C 经过点 (0, 3) ,方程 2 3 0ax bx a 的两根 为 1x , 2x ,且 1 2 4x x 。 (1)求抛物线 1C 的顶点坐标. (2)已知实数 0x ,请证明: 1x x ≥ 2 ,并说明 x 为何值时才会有 1 2x x . (3)若抛物线先向上平移 4 个单位,再向左平移 1 个单位后得到抛物线 2C ,设 1( , )A m y , 2( , )B n y 是 2C 上的两个不同点,且满足: 090AOB , 0m , 0n . 请你用含有 m 的表达式表示出△ AOB 的面积 S ,并求出 S 的最小值及 S 取最小值时一 次函数OA 的函数解析式。 (参考公式:在平面直角坐标系中,若 1 1( , )P x y , 2 2( , )Q x y ,则 P ,Q 两点间的距离 为 2 2 2 1 2 1( ) ( )x x y y ) 【考点】二次函数综合题. 【专题】压轴题;配方法. 【分析】(1)求抛物线的顶点坐标,需要先求出抛物线的解析式,即确定待定系数 a、 b 的值.已知抛物线图象与 y 轴交点,可确定解析式中的常数项(由此得 到 a 的值);然后从方程入手求 b 的值,题干给出了两根差的绝对值,将 其进行适当变形(转化为两根和、两根积的形式),结合根与系数的关系 即可求出 b 的值. (2) 1 1x x ,因此将 1x x 配成完全平方式,然后根据平方的非负性即可得 证. (3)结合(1)的抛物线的解析式以及函数的平移规律,可得出抛物线 C2 的解 析式;在 Rt△OAB 中,由勾股定理可确定 m、n 的关系式,然后用 m 列 出△AOB 的面积表达式,结合不等式的相关知识可确定△OAB 的最小面积 值以及此时 m 的值,进而由待定系数法确定一次函数 OA 的解析式. 【解答】解:(1)∵抛物线过(0,-3)点,∴-3a=-3 ∴a=1 ……………………………………1分 ∴y=x2+bx-3 ∵x2+bx-3=0的两根为 x1,x2 且 21 x-x =4 ∴ 21 2 2121 4)( xxxxxx =4且 b<0 ∴b=-2 ……………………1分 ∴y=x2-2x-3=(x-1)2-4 ∴抛物线C1的顶点坐标为(1,-4) ………………………1分 (2)∵x>0,∴ 0)1(21 x xxx ∴ ,21 xx 显然当 x=1时,才有 ,21 xx ………………………2分 (3)方法一:由平移知识易得C2的解析式为:y=x2 ………………………1分 ∴A(m,m2),B(n,n2) ∵ΔAOB 为 RtΔ ∴OA2+OB2=AB2 ∴m2+m4+n2+n4=(m-n)2+(m2-n2)2 化简得:m n=-1 ……………………1分 ∵SΔAOB= OBOA 2 1 = 4242 2 1 nnmm ∵m n=-1 ∴SΔAOB= 2 222 122 122 1 m mnm = 122 11 2 1)1(2 1 2 mmmm ∴SΔAOB 的最小值为1,此时 m=1,A(1,1) ……………………2分 ∴直线 OA 的一次函数解析式为y=x ……………………1分 方法二:由题意可求抛物线 2C 的解析式为: 2y x ································(1 分) ∴ 2( , )A m m , 2( , )B n n 过点 A 、 B 作 x 轴的垂线,垂足分别为 C 、 D ,则 AOC BODACDBS S S S 梯形 2 2 2 21 1 1( )( )2 2 2m n m n m m n n 1 ( )2 mn m n 由 BOD△ ∽ OAC△ 得 BD OD OC AC 即 2 2 n n m m ∴ 1mn ·············································································(1 分) ∴ 1n m ∴ 1 ( )2S mn m n 1 1( )2 m m 由(2)知: 1 2m m ∴ 1 1 1( ) 2 12 2S m m 当且仅当 1m , S 取得最小值 1 此时 A 的坐标为(1,1)······················································ (2 分) ∴一次函数OA的解析式为 y x ················································(1 分) 【点评】该题考查了二次函数解析式的确定、函数图象的平移、不等式的应用等知识, B(n,n2) A(m,m2) O CD y x 解题过程中完全平方式的变形被多次提及,应熟练掌握并能灵活应用. (2.2012 滨州)24.如图,在平面直角坐标系中,抛物线 y=ax2+bx+c 经过 A(﹣2,﹣ 4),O(0,0),B(2,0)三点. (1)求抛物线 y=ax2+bx+c 的解析式; (2)若点 M 是该抛物线对称轴上的一点,求 AM+OM 的最小值. 考点:二次函数综合题。 解答:解:(1)把 A(﹣2,﹣4),O(0,0),B(2,0)三点的坐标代入 y=ax2+bx+c 中,得 解这个方程组,得 a=﹣ ,b=1,c=0 所以解析式为 y=﹣ x2+x. (2)由 y=﹣ x2+x=﹣ (x﹣1)2+ ,可得 抛物线的对称轴为 x=1,并且对称轴垂直平分线段 OB ∴OM=BM ∴OM+AM=BM+AM 连接 AB 交直线 x=1 于 M 点,则此时 OM+AM 最小 过点 A 作 AN⊥x 轴于点 N, 在 Rt△ABN 中,AB= = =4 , 因此 OM+AM 最小值为 . (3.2012 滨州)25.如图 1,l1,l2,l3,l4 是一组平行线,相邻 2 条平行线间的距离都是 1 个单位长度,正方形 ABCD 的 4 个顶点 A,B,C,D 都在这些平行线上.过点 A 作 AF⊥l3 于点 F,交 l2 于点 H,过点 C 作 CE⊥l2 于点 E,交 l3 于点 G. (1)求证:△ADF≌△CBE; (2)求正方形 ABCD 的面积; (3)如图 2,如果四条平行线不等距,相邻的两条平行线间的距离依次为 h1,h2,h3,试 用 h1,h2,h3 表示正方形 ABCD 的面积 S. 考点:全等三角形的判定与性质;平行线之间的距离;正方形的性质。 解答:证明:(1)在 Rt△AFD 和 Rt△CEB 中, ∵AD=BC,AF=CE, ∴Rt△AFD≌Rt△CEB; (2)∵∠ABH+∠CBE=90°,∠ABH+∠BAH=90°, ∴∠CBE=∠BAH 又∵AB=BC,∠AHB=∠CEB=90° ∴△ABH≌△BCE, 同理可得,△ABH≌△BCE≌△CDG≌△DAF, ∴S 正方形 ABCD=4S△ABH+S 正方形 HEGF =4× ×2×1+1×1 =5; (3)由(1)知,△AFD≌△CEB,故 h1=h3, 由(2)知,△ABH≌△BCE≌△CDG≌△DAF, ∴S 正方形 ABCD=4S△ABH+S 正方形 HEGF =4× (h1+h2)•h1+h2 2=2h1 2+2h1h2+h2 2. (4.2012 云南)22.如图,在矩形 ABCD 中,对角线 BD 的垂直平分线 MN 与 AD 相交于点 M,与 BD 相交于点 N,连接 BM,DN. (1)求证:四边形 BMDN 是菱形; (2)若 AB=4,AD=8,求 MD 的长. 考点: 矩形的性质;线段垂直平分线的性质;勾股定理;平行四边形的判定;菱形的性质; 菱形的判定。 专题: 计算题;证明题。 分析: (1)根据矩形性质求出 AD∥BC,根据 OB=OD 和 AD∥BC 推出 OM=ON,得出 平行四边形 BMDN,推出菱形 BMDN; (2)根据菱形性质求出 DM=BM,在 Rt△AMB 中,根据勾股定理得出 BM2=AM2+AB2,推出 x2=x2﹣16x+64+16,求出即可. 解答: (1)证明:∵四边形 ABCD 是矩形, ∴AD∥BC,∠A=90°, ∵MN 是 BD 的中垂线, ∴OB=OD,BD⊥MN, = , ∴BM=DM, ∵OB=OD, ∴四边形 BMDN 是平行四边形, ∵MN⊥BD, ∴平行四边形 BMDN 是菱形. (2)解:∵四边形 BMDN 是菱形, ∴MB=MD, 设 MD 长为 x,则 MB=DM=x, 在 Rt△AMB 中,BM2=AM2+AB2 即 x2=(8﹣x)2+42, 解得:x=5, 答:MD 长为 5. 点评: 本题考查了矩形性质,平行四边形的判定,菱形的判定和性质,勾股定理等知识点 的应用,对角线互相平分的四边形是平行四边形,对角线互相垂直的平行四边形是 菱形. (5.2012 云南)23.如图,在平面直角坐标系中,直线 y= x+2 交 x 轴于点 P,交 y 轴 于点 A.抛物线 y= x2+bx+c 的图象过点 E(﹣1,0),并与直线相交于 A、B 两点. (1)求抛物线的解析式(关系式); (2)过点 A 作 AC⊥AB 交 x 轴于点 C,求点 C 的坐标; (3)除点 C 外,在坐标轴上是否存在点 M,使得△MAB 是直角三角形?若存在,请求出 点 M 的坐标;若不存在,请说明理由. 考点: 二次函数综合题。 分析: (1)首先求出 A 点坐标,然后利用待定系数法求出抛物线的解析式; (2)利用相似三角形(Rt△OCA∽Rt△OPA)比例线段之间的关系,求出线段 OC 的 长度,从而得到 C 点的坐标,如题图所示; (3)存在所求的 M 点,在 x 轴上有 3 个,y 轴上有 2 个,注意不要遗漏.求点 M 坐标的过程并不复杂,但要充分利用相似三角形比例线段之间的关系. 解答: 解:(1)直线解析式为 y= x+2,令 x=0,则 y=2, ∴A(0,2), ∵抛物线 y= x2+bx+c 的图象过点 A(0,2),E(﹣1,0), ∴ , 解得 . ∴抛物线的解析式为:y= x2+ x+2. (2)∵直线 y= x+2 分别交 x 轴、y 轴于点 P、点 A, ∴P(6,0),A(0,2), ∴OP=6,OA=2. ∵AC⊥AB,OA⊥OP, ∴Rt△OCA∽Rt△OPA,∴ , ∴OC= , 又 C 点在 x 轴负半轴上, ∴点 C 的坐标为 C( ,0). (3)抛物线 y= x2+ x+2 与直线 y= x+2 交于 A、B 两点, 令 x2+ x+2= x+2, 解得 x1=0,x2= , ∴B( , ). 如答图①所示,过点 B 作 BD⊥x 轴于点 D, 则 D( ,0),BD= ,DP=6﹣ = . 点 M 在坐标轴上,且△MAB 是直角三角形,有以下几种情况: ①当点 M 在 x 轴上,且 BM⊥AB,如答图①所示. 设 M(m,0),则 MD= ﹣m. ∵BM⊥AB,BD⊥x 轴,∴ , 即 , 解得 m= , ∴此时 M 点坐标为( ,0); ②当点 M 在 x 轴上,且 BM⊥AM,如答图①所示. 设 M(m,0),则 MD= ﹣m. ∵BM⊥AM,易知 Rt△AOM∽Rt△MDB, ∴ ,即 , 化简得:m2﹣ m+ =0, 解得:x1= ,x2= , ∴此时 M 点坐标为( ,0),( ,0); (说明:此时的 M 点相当于以 AB 为直径的圆与 x 轴的两个交点) ③当点 M 在 y 轴上,且 BM⊥AM,如答图②所示. 此时 M 点坐标为(0, ); ④当点 M 在 y 轴上,且 BM′⊥AB,如答图②所示. 设 M′(0,m),则 AM=2﹣ = ,BM= ,MM′= ﹣m. 易知 Rt△ABM∽Rt△MBM′, ∴ ,即 , 解得 m= , ∴此时 M 点坐标为(0, ). 综上所述,除点 C 外,在坐标轴上存在点 M,使得△MAB 是直角三角形. 符合条件的点 M 有 5 个,其坐标分别为:( ,0)、( ,0)、( , 0)、(0, )或(0, ). 点评: 本题综合考查了二次函数的图象与性质、待定系数法求函数解析式、一次函数、解 一元二次方程、相似三角形的判定与性质等重要知识点.难点在于第(3)问,所求 的 M 点有 5 个(x 轴上有 3 个,y 轴上有 2 个),需要分情况讨论,不要遗漏. (6.2012 岳阳)25.(1)操作发现:如图①,D 是等边△ABC 边 BA 上一动点(点 D 与点 B 不重合),连接 DC,以 DC 为边在 BC 上方作等边△DCF,连接 AF.你能发现线段 AF 与 BD 之间的数量关系吗?并证明你发现的结论. (2)类比猜想:如图②,当动点 D 运动至等边△ABC 边 BA 的延长线上时,其他作法与(1) 相同,猜想 AF 与 BD 在(1)中的结论是否仍然成立? (3)深入探究: Ⅰ.如图③,当动点 D 在等边△ABC 边 BA 上运动时(点 D 与点 B 不重合)连接 DC,以 DC 为边在 BC 上方、下方分别作等边△DCF 和等边△DCF′,连接 AF、BF′,探究 AF、BF′ 与 AB 有何数量关系?并证明你探究的结论. Ⅱ.如图④,当动点 D 在等边△边 BA 的延长线上运动时,其他作法与图③相同,Ⅰ中的结 论是否成立?若不成立,是否有新的结论?并证明你得出的结论. 考点: 全等三角形的判定与性质;等边三角形的性质。 专题: 几何综合题。 分析: (1)根据等边三角形的三条边、三个内角都相等的性质,利用全等三角形的判定定 理 SAS 可以证得△BCD≌△ACF;然后由全等三角形的对应边相等知 AF=BD; (2)通过证明△BCD≌△ACF,即可证明 AF=BD; (3)Ⅰ.AF+BF′=AB;利用全等三角形△BCD≌△ACF(SAS)的对应边 BD=AF; 同理△BCF′≌△ACD(SAS),则 BF′=AD,所以 AF+BF′=AB; Ⅱ.Ⅰ中的结论不成立.新的结论是 AF=AB+BF′;通过证明△BCF′≌△ACD(SAS), 则 BF′=AD(全等三角形的对应边相等);再结合(2)中的结论即可证得 AF=AB+BF′. 解答: 解:(1)AF=BD; 证明如下:∵△ABC 是等边三角形(已知), ∴BC=AC,∠BCA=60°(等边三角形的性质); 同理知,DC=CF,∠DCF=60°; ∴∠BCA﹣∠DCA=∠DCF﹣DCA,即∠BCD=∠ACF; 在△BCD 和△ACF 中, , ∴△BCD≌△ACF(SAS), ∴BD=AF(全等三角形的对应边相等); (2)证明过程同(1),证得△BCD≌△ACF(SAS),则 AF=BD(全等三角形的对应 边相等),所以,当动点 D 运动至等边△ABC 边 BA 的延长线上时,其他作法与(1) 相同,AF=BD 仍然成立; (3)Ⅰ.AF+BF′=AB; 证明如下:由(1)知,△BCD≌△ACF(SAS),则 BD=AF; 同理△BCF′≌△ACD(SAS),则 BF′=AD, ∴AF+BF′=BD+AD=AB; Ⅱ.Ⅰ中的结论不成立.新的结论是 AF=AB+BF′; 证明如下:在△BCF′和△ACD 中, , ∴△BCF′≌△ACD(SAS), ∴BF′=AD(全等三角形的对应边相等); 又由(2)知,AF=BD; ∴AF=BD=AB+AD=AB+BF′,即 AF=AB+BF′. 点评: 本题考查了全等三角形的判定与性质、等边三角形的性质.等边三角形的三条边都 相等,三个内角都是 60°. (7.2012 岳阳)26.我们常见的炒菜锅和锅盖都是抛物线面,经过锅心和盖心的纵断面是两 端抛物线组合而成的封闭图形,不妨简称为“锅线”,锅口直径为 6dm,锅深 3dm,锅盖 高 1dm(锅口直径与锅盖直径视为相同),建立直接坐标系如图①所示,如果把锅纵断面的 抛物线的记为 C1,把锅盖纵断面的抛物线记为 C2. (1)求 C1 和 C2 的解析式; (2)如图②,过点 B 作直线 BE:y= x﹣1 交 C1 于点 E(﹣2,﹣ ),连接 OE、BC,在 x 轴上求一点 P,使以点 P、B、C 为顶点的△PBC 与△BOE 相似,求出 P 点的坐标; (3)如果(2)中的直线 BE 保持不变,抛物线 C1 或 C2 上是否存在一点 Q,使得△EBQ 的 面积最大?若存在,求出 Q 的坐标和△EBQ 面积的最大值;若不存在,请说明理由. 考点: 二次函数综合题。 专题: 压轴题;分类讨论。 分析: (1)已知 A、B、C、D 四点坐标,利用待定系数法即可确定两函数的解析式. (2)根据直线 BE:y= x﹣1 知,该直线必过(0,﹣1)点,那么∠EBO=∠CBO, 若以点 P、B、C 为顶点的△PBC 与△BOE 相似,那么夹这组对应角的对应边必成比 例,先求出 BC、BO、BE 的长,然后分情况根据线段间的比例关系求出 BP 的长, 进而得到 OP 的长,即可确定 P 点坐标. (3)△EBQ 中,BE 长为定值,若以 BE 为底,当△EBQ 的面积最大时,Q 到直线 BE 的距离最大;由于点 Q 可能在抛物线 C1 或 C2 上,因此两种情况都要解一下,最后 通过比较得到能使△EBQ 面积最大的 Q 点.首先作直线 l∥BE,分别令直线 l 与抛物 线 C1、C2 有且仅有一个交点,那么符合条件的 Q 点必在这两个交点中,先求出这两 个交点分别到直线 BE 的距离,距离大者符合条件,由此可得到 Q 点坐标和△EBQ 的 面积最大值. 解答: 解:(1)由于抛物线 C1、C2 都过点 A(﹣3,0)、B(3,0),可设它们的解析式为: y=a(x﹣3)(x+3); 抛物线 C1 还经过 D(0,﹣3),则有: ﹣3=a(0﹣3)(0+3),a= 即:抛物线 C1:y= x2﹣3(﹣3≤x≤3); 抛物线 C2 还经过 A(0,1),则有: 1=a(0﹣3)(0+3),a=﹣ 即:抛物线 C2:y=﹣ x2+1(﹣3≤x≤3). (2)由于直线 BE:y= x﹣1 必过(0,﹣1),所以∠CBO=∠EBO (tan∠CBO=tan∠EBO= ); 由 E 点坐标可知:tan∠AOE≠ ,即∠AOE≠∠CBO,所以它们的补角∠EOB≠∠CBx; 若以点 P、B、C 为顶点的△PBC 与△BOE 相似,只需考虑两种情况: ①∠CBP1=∠EBO,且 OB:BE=BP1:BC,即: 3: =BP1: ,得:BP1= ,OP1=OB﹣BP1= ; ∴P1( ,0); ②∠P2BC=∠EBO,且 BC:BP2=OB:BE,即: :BP2=3: ,得:BP2= ,OP2=BP2﹣OB= ; ∴P2(﹣ ,0). 综上,符合条件的 P 点有:P1( ,0)、P2(﹣ ,0). (3)如图,作直线 l∥直线 BE,设直线 l:y= x+b; ①当直线 l 与抛物线 C1 只有一个交点时: x+b= x2﹣3,即:x2﹣x﹣(3b+9)=0 ∴该交点 Q2( ,﹣ ); Q2 到直线 BE: x﹣y﹣1=0 的距离: = = ; ②当直线 l 与抛物线 C2 只有一个交点时: x+b=﹣ x2+1,即:x2+3x+9b﹣9=0 ∴该交点 Q1(﹣ , ); Q1 到直线 BE: x﹣y﹣1=0 的距离: = ; ∴符合条件的 Q 点为 Q1(﹣ , ); △EBQ 的最大面积:Smax= ×BE× = . 点评: 考查了二次函数综合题.该题的难度和计算量都比较大,涉及了函数解析式的确定、 相似三角形的判定和性质、图形面积的解法等重点知识;解答(2)题时,应注意分 不同的对应边来进行讨论,以免漏解.(3)的难度较大,点到直线的距离公式【点 (x0,y0)到直线(Ax+By+C=0)的距离为:d= 】是需要记住的 内容.另外,题目在设计时结合了一定的生活元素,形式较为新颖. (8.2012 苏州)28.如图,正方形 ABCD 的边 AD 与矩形 EFGH 的边 FG 重合,将正方形 ABCD 以 1cm/s 的速度沿 FG 方向移动,移动开始前点 A 与点 F 重合,在移动过程中,边 AD 始终与边 FG 重合,连接 CG,过点 A 作 CG 的平行线交线段 GH 于点 P,连接 PD.已 知正方形 ABCD 的边长为 1cm,矩形 EFGH 的边 FG,GH 的长分别为 4cm,3cm,设正 方形移动时间为 x(s),线段 GP 的长为 y(cm),其中 0≤x≤2.5. (1)试求出 y 关于 x 的函数关系式,并求当 y=3 时相应 x 的值; (2)记△DGP 的面积为 S1,△CDG 的面积为 S2.试说明 S1﹣S2 是常数; (3)当线段 PD 所在直线与正方形 ABCD 的对角线 AC 垂直时,求线段 PD 的长. 考点: 正方形的性质;一元二次方程的应用;等腰直角三角形;矩形的性质;解直角三角 形。 专题: 代数几何综合题。 分析: (1)根据题意表示出 AG、GD 的长度,再由△GCD∽△APG,利用对应边成比例可 解出 x 的值. (2)利用(1)得出的 y 与 x 的关系式表示出 S1、S2,然后作差即可. (3)延长 PD 交 AC 于点 Q,然后判断△DGP 是等腰直角三角形,从而结合 x 的范 围得出 x 的值,在 Rt△DGP 中,解直角三角形可得出 PD 的长度. 解答: 解:(1)∵CG∥AP, ∴△GCD∽△APG, ∴ = , ∵GF=4,CD=DA=1,AF=x, ∴GD=3﹣x,AG=4﹣x, ∴ = ,即 y= , ∴y 关于 x 的函数关系式为 y= , 当 y=3 时, =3,解得 x=2.5, 经检验的 x=2.5 是分式方程的根. 故 x 的值为 2.5; (2)∵S1= GP•GD= • •(3﹣x)= , S2= GD•CD= (3﹣x)1= , ∴S1﹣S2= ﹣ = 即为常数; (3)延长 PD 交 AC 于点 Q. ∵正方形 ABCD 中,AC 为对角线, ∴∠CAD=45°, ∵PQ⊥AC, ∴∠ADQ=45°, ∴∠GDP=∠ADQ=45°. ∴△DGP 是等腰直角三角形,则 GD=GP, ∴3﹣x= , 化简得:x2﹣5x+5=0. 解得:x= , ∵0≤x≤2.5, ∴x= , 在 Rt△DGP 中,PD= = (3﹣x)= . 点评: 此题考查了正方形的性质、等腰三角形的性质及解直角三角形的知识,解答本题的 关键是用移动的时间表示出有关线段的长度,然后运用所学知识进行求解. (9.2012 苏州)29.如图,已知抛物线 y= x2﹣ (b+1)x+ (b 是实数且 b>2)与 x 轴 的正半轴分别交于点 A、B(点 A 位于点 B 的左侧),与 y 轴的正半轴交于点 C. (1)点 B 的坐标为 (b,0) ,点 C 的坐标为 (0, ) (用含 b 的代数式表示); (2)请你探索在第一象限内是否存在点 P,使得四边形 PCOB 的面积等于 2b,且△PBC 是 以点 P 为直角顶点的等腰直角三角形?如果存在,求出点 P 的坐标;如果不存在,请说明 理由; (3)请你进一步探索在第一象限内是否存在点 Q,使得△QCO,△QOA 和△QAB 中的任意 两个三角形均相似(全等可作相似的特殊情况)?如果存在,求出点 Q 的坐标;如果不存 在,请说明理由. 考点: 二次函数综合题。 分析: (1)令 y=0,即 y= x2﹣ (b+1)x+ =0,解关于 x 的一元二次方程即可求出 A, B 横坐标,令 x=0,求出 y 的值即 C 的纵坐标; (2)存在,先假设存在这样的点 P,使得四边形 PCOB 的面积等于 2b,且△PBC 是以点 P 为直角顶点的等腰直角三角形.设点 P 的坐标为(x,y),连接 OP,过 P 作 PD⊥x 轴,PE⊥y 轴,垂足分别为 D、E,利用已知条件证明△PEC≌△PDB,进而 求出 x 和 y 的值,从而求出 P 的坐标; (3)存在,假设存在这样的点 Q,使得△QCO,△QOA 和△QAB 中的任意两个三角 形均相似,有条件可知:要使△QOA 与△QAB 相似,只能∠QAO=∠BAQ=90°,即 QA⊥x 轴; 要使△QOA 与△OQC 相似,只能∠QCO=90°或∠OQC=90°;再分别讨论求出满足 题意 Q 的坐标即可. 解答: 解:(1)令 y=0,即 y= x2﹣ (b+1)x+ =0, 解得:x=1 或 b, ∵b 是实数且 b>2,点 A 位于点 B 的左侧, ∴点 B 的坐标为(b,0), 令 x=0, 解得:y= , ∴点 C 的坐标为(0, ), 故答案为:(b,0),(0, ); (2)存在, 假设存在这样的点 P,使得四边形 PCOB 的面积等于 2b,且△PBC 是以点 P 为直角 顶点的等腰直角三角形. 设点 P 的坐标为(x,y),连接 OP. 则 S 四边形 POCB=S△PCO+S△POB= • •x+ •b•y=2b, ∴x+4y=16. 过 P 作 PD⊥x 轴,PE⊥y 轴,垂足分别为 D、E, ∴∠PEO=∠EOD=∠ODP=90°. ∴四边形 PEOD 是矩形. ∴∠EPO=90°. ∴∠EPC=∠DPB. ∴△PEC≌△PDB,∴PE=PD,即 x=y. 由 解得 由△PEC≌△PDB 得 EC=DB,即 ﹣ =b﹣ , 解得 b= >2 符合题意. ∴P 的坐标为( , ); (3)假设存在这样的点 Q,使得△QCO,△QOA 和△QAB 中的任意两个三角形均相 似. ∵∠QAB=∠AOQ+∠AQO, ∴∠QAB>∠AOQ,∠QAB>∠AQO. ∴要使△QOA 与△QAB 相似,只能∠QAO=∠BAQ=90°,即 QA⊥x 轴. ∵b>2, ∴AB>OA, ∴∠Q0A>∠ABQ. ∴只能∠AOQ=∠AQB.此时∠OQB=90°, 由 QA⊥x 轴知 QA∥y 轴. ∴∠COQ=∠OQA. ∴要使△QOA 与△OQC 相似,只能∠QCO=90°或∠OQC=90°. (I)当∠OCQ=90°时,△CQO≌△QOA. ∴AQ=CO= . 由 AQ=AQ2=OA•AB 得:( )2=b﹣1. 解得:b=8±4 . ∵b>2, ∴b=8+4 . ∴点 Q 的坐标是(1,2+ ). (II)当∠OQC=90°时,△QCO∽△QOA, ∴ = ,即 OQ2=OC•AQ. 又 OQ2=OA•OB, ∴OC•AQ=OA•OB.即 •AQ=1×b. 解得:AQ=4,此时 b=17>2 符合题意, ∴点 Q 的坐标是(1,4). ∴综上可知,存在点 Q(1,2+ )或 Q(1,4),使得△QCO,△QOA 和△QAB 中的任意两个三角形均相似. 点评: 此题是一道综合题,难度较大,主要考查二次函数的性质,全等三角形的判定和性 质,以及相似三角形的判定和性质,还考查等腰三角形的性质及勾股定理,同时还 让学生探究存在性问题,对待问题要思考全面,学会分类讨论的思想. (10. 2012 广东深圳 9 分)22.如图,已知△ABC 的三个顶点坐标分别为 A(-4,0)、B(1, 0)、C(-2,6). (1)求经过 A、B、C 三点的抛物线解析式; (2)设直线 BC 交 y 轴于点 E,连接 AE,求证:AE=CE; (3)设抛物线与 y 轴交于点 D,连接 AD 交 BC 于点 F,试问以 A、B、F,为顶点的三角形与 △ABC 相似吗? 请说明理由. 【答案】解:(1)∵抛物线经过 A(-4,0)、B(1,0),∴设函数解析式为:y=a(x+4) (x-1)。 又∵由抛物线经过 C(-2,6),∴6=a(-2+4)(-2-1),解得: a=-1。 ∴经过 A、B、C 三点的抛物线解析式为:y=-(x+4)(x-1),即 y= -x2-3x+4。 (2)证明:设直线 BC 的函数解析式为 y=kx+b, 由题意得: k b 0 2k b 6 ,解得: k 2 b 2 。 ∴直线 BC 的解析式为 y=-2x+2. ∴点 E 的坐标为(0,2)。 ∴ 2 22 2 2 2 AE AO OE 4 2 2 5 CE 2 0 6 2 2 5 , 。 ∴AE=CE。 (3)相似。理由如下: 设直线 AD 的解析式为 y=k1x+b1,则 1 1 1 4k b 0 b 4 ,解得: 1 1 k 1 b 4 。 ∴直线 AD 的解析式为 y=x+4。 联立直线 AD 与直线 BC 的函数解析式可得: y x 4 y 2x 2 ,解得: 2 x 3 10 y 3 。 ∴点 F 的坐标为( 2 10 3 3 , )。 则 2 2 2 22 10 5 5 2 10 10 2BF 1 0 AF 4 1 03 3 3 3 3 3 , 。 又∵AB=5, 2 2BC 2 1 6 0 3 5 , ∴ BF 5 AB 5 AB 3 BC 3 , 。∴ BF AB AB BC 。 又∵∠ABF=∠CBA,∴△ABF∽△CBA。 ∴以 A、B、F 为顶点的三角形与△ABC 相似。 【考点】二次函数综合题,待定系数法,曲线上点的坐标与方程的关系,勾股定理,相似三 角形的判定。 【分析】(1)利用待定系数法求解即可得出抛物线的解析式。 (2)求出直线 BC 的函数解析式,从而得出点 E 的坐标,然后分别求出 AE 及 CE 的长度即可证明出结论。 (3)求出 AD 的函数解析式,然后结合直线 BC 的解析式可得出点 F 的坐标,根据勾股定 理分别求出 BF,BC 得出 BF AB AB BC ;由题意得∠ABF=∠CBA, 即可作出判断。 【11. 2012 成都】 28. (本小题满分 l2 分) 如图,在平面直角坐标系 xOy 中,一次函数 5 4y x m ( m 为常数)的图象与 x 轴交 于点A( 3 ,0),与y轴交于点C.以直线x=1为对称轴的抛物线 2y ax bx c ( a b c, , 为常数,且 a ≠0)经过 A,C 两点,并与 x 轴的正半轴交于点 B. (1)求 m 的值及抛物线的函数表达式; (2)设 E 是 y 轴右侧抛物线上一点,过点 E 作直线 AC 的平行线交 x 轴于点 F.是否存 在这样的点 E,使得以 A,C,E,F 为顶点的四边形是平行四边形?若存在,求出点 E 的坐 标及相应的平行四边形的面积;若不存在,请说明理由; (3)若 P 是抛物线对称轴上使△ACP 的周长取得最小值的点,过点 P 任意作一条与 y 轴 不平行的直线交抛物线于 1 1 1M ( )x y, , 2 2 2M ( )x y, 两点,试探究 21 1 2 P PM M M M 是否为定 值,并写出探究过程. 考点:二次函数综合题。 解答:解:(1)∵ 经过点(﹣3,0), ∴0= +m,解得 m= , ∴直线解析式为 ,C(0, ). ∵抛物线 y=ax2+bx+c 对称轴为 x=1,且与 x 轴交于 A(﹣3,0),∴另一交点为 B(5,0), 设抛物线解析式为 y=a(x+3)(x﹣5), ∵抛物线经过 C(0, ), ∴ =a•3(﹣5),解得 a= , ∴抛物线解析式为 y= x2+ x+ ; (2)假设存在点 E 使得以 A、C、E、F 为顶点的四边形是平行四边形, 则 AC∥EF 且 AC=EF.如答图 1, (i)当点 E 在点 E 位置时,过点 E 作 EG⊥x 轴于点 G, ∵AC∥EF,∴∠CAO=∠EFG, 又∵ ,∴△CAO≌△EFG, ∴EG=CO= ,即 yE= , ∴ = xE 2+ xE+ ,解得 xE=2(xE=0 与 C 点重合,舍去), ∴E(2, ),S▱ACEF= ; (ii)当点 E 在点 E′位置时,过点 E′作 E′G′⊥x 轴于点 G′, 同理可求得 E′( +1, ),S▱ACE′F′= . (3)要使△ACP 的周长最小,只需 AP+CP 最小即可. 如答图 2,连接 BC 交 x=1 于 P 点,因为点 A、B 关于 x=1 对称,根据轴对称性质以及两 点之间线段最短,可知此时 AP+CP 最小(AP+CP 最小值为线段 BC 的长度). ∵B(5,0),C(0, ),∴直线 BC 解析式为 y= x+ , ∵xP=1,∴yP=3,即 P(1,3). 令经过点 P(1,3)的直线为 y=kx+3﹣k, ∵y=kx+3﹣k,y= x2+ x+ , 联立化简得:x2+(4k﹣2)x﹣4k﹣3=0, ∴x1+x2=2﹣4k,x1x2=﹣4k﹣3. ∵y1=kx1+3﹣k,y2=kx2+3﹣k,∴y1﹣y2=k(x1﹣x2). 根据两点间距离公式得到: M1M2= = = ∴M1M2= = =4(1+k2). 又 M1P= = = ; 同理 M2P= ∴M1P•M2P=(1+k2)• =(1+k2) • =(1+k2)• =4(1+k2). ∴M1P•M2P=M1M2, ∴ =1 为定值. 【12.2012 聊城】 25.某电子厂商投产一种新型电子厂品,每件制造成本为 18 元,试销过程中发现,每月销 售量 y(万件)与销售单价 x(元)之间的关系可以近似地看作一次函数 y=﹣2x+100.(利 润=售价﹣制造成本) (1)写出每月的利润 z(万元)与销售单价 x(元)之间的函数关系式; (2)当销售单价为多少元时,厂商每月能获得 3502 万元的利润?当销售单价为多少元时, 厂商每月能获得最大利润?最大利润是多少? (3)根据相关部门规定,这种电子产品的销售单价不能高于 32 元,如果厂商要获得每月 不低于 350 万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元? 考点:二次函数的应用;一次函数的应用。 分析:(1)根据每月的利润 z=(x﹣18)y,再把 y=﹣2x+100 代入即可求出 z 与 x 之间 的函数解析式, (2)把 z=350 代入 z=﹣2x2+136x﹣1800,解这个方程即可,将 z═﹣2x2+136x ﹣1800 配方,得 z=﹣2(x﹣34)2+512,即可求出当销售单价为多少元时,厂商 每月能获得最大利润,最大利润是多少. (3)结合(2)及函数 z=﹣2x2+136x﹣1800 的图象即可求出当 25≤x≤43 时 z≥350, 再根据限价 32 元,得出 25≤x≤32,最后根据一次函数 y=﹣2x+100 中 y 随 x 的增 大而减小,即可得出当 x=32 时,每月制造成本最低,最低成本是 18×(﹣2×32+100) 解答:解:(1)z=(x﹣18)y=(x﹣18)(﹣2x+100) =﹣2x2+136x﹣1800, ∴z 与 x 之间的函数解析式为 z=﹣2x2+136x﹣1800; (2)由 z=350,得 350=﹣2x2+136x﹣1800, 解这个方程得 x1=25,x2=43 所以,销售单价定为 25 元或 43 元, 将 z═﹣2x2+136x﹣1800 配方,得 z=﹣2(x﹣34)2+512, 因此,当销售单价为 34 元时,每月能获得最大利润,最大利润是 512 万元; (3)结合(2)及函数 z=﹣2x2+136x﹣1800 的图象(如图所示)可知, 当 25≤x≤43 时 z≥350, 又由限价 32 元,得 25≤x≤32, 根据一次函数的性质,得 y=﹣2x+100 中 y 随 x 的增大而减小, ∴当 x=32 时,每月制造成本最低.最低成本是 18×(﹣2×32+100)=648(万元), 因此,所求每月最低制造成本为 648 万元. 点评:本题考查的是二次函数在实际生活中的应用,关键是根据题意求出二次函数的解析 式,综合利用二次函数和一次函数的性质解决实际问题. 【13. 2012 安徽】 23. 如图,排球运动员站在点 O 处练习发球,将球从 O 点正上方 2m 的 A 处发出,把球看 成点,其运行的高度 y(m)与运行的水平距离 x(m)满足关系式 y=a(x-6)2+h.已知球网与 O 点的水平距离为 9m,高度为 2.43m,球场的边界距 O 点的水平距离为 18m。 (1)当 h=2.6 时,求 y 与 x 的关系式(不要求写出自变量 x 的取值范围) (2)当 h=2.6 时,球能否越过球网?球会不会出界?请说明理由; (3)若球一定能越过球网,又不出边界,求 h 的取值范围。 23.解析:(1)根据函数图象上面的点的坐标应该满足函数解析式,把 x=0,y=2,及 h=2.6 代入到 y=a(x-6)2+h 中即可求函数解析式;(2)根据函数解析式确定函数图象上点的坐标, 并解决时间问题;(3)先把 x=0,y=2,代入到 y=a(x-6)2+h 中求出 36 2 ha ;然后分别表 示出 x=9,x=18 时,y 的值应满足的条件,解得即可. 解:(1)把 x=0,y=2,及 h=2.6 代入到 y=a(x-6)2+h 即 2=a(0-6)2+2.6, ∴ 60 1a ∴y= 60 1 (x-6)2+2.6 (2)当 h=2.6 时,y= 60 1 (x-6)2+2.6 x=9 时,y= 60 1 (9-6)2+2.6=2.45>2.43 第 23 题图 ∴球能越过网 x=18 时,y= 60 1 (18-6)2+2.6=0.2>0 ∴球会过界 (3)x=0,y=2,代入到 y=a(x-6)2+h 得 36 2 ha ; x=9 时,y= 36 2 h (9-6)2+h 4 32 h >2.43 ① x=18 时,y= 36 2 h (18-6)2+h h38 >0 ② 由① ②得 h≥ 3 8 点评:本题是二次函数问题,利用函数图象上点的坐标确定函数解析式,然后根据函数性质 来结合实际问题求解. 【14. 2012 乐山】 26.如图,在平面直角坐标系中,点 A 的坐标为(m,m),点 B 的坐标为(n,﹣n),抛 物线经过 A、O、B 三点,连接 OA、OB、AB,线段 AB 交 y 轴于点 C.已知实数 m、n(m <n)分别是方程 x2﹣2x﹣3=0 的两根. (1)求抛物线的解析式; (2)若点 P 为线段 OB 上的一个动点(不与点 O、B 重合),直线 PC 与抛物线交于 D、E 两点(点 D 在 y 轴右侧),连接 OD、BD. ①当△OPC 为等腰三角形时,求点 P 的坐标; ②求△BOD 面积的最大值,并写出此时点 D 的坐标. 考点:二次函数综合题。 分析:(1)首先解方程得出 A,B 两点的坐标,进而利用待定系数法求出二次函数解析式 即可; (2)①首先求出 AB 的直线解析式,以及 BO 解析式,再利用等腰三角形的性质得 出当 OC=OP 时,当 OP=PC 时,点 P 在线段 OC 的中垂线上,当 OC=PC 时分别 求出 x 的值即可; ②利用 S△BOD=S△ODQ+S△BDQ 得出关于 x 的二次函数,进而得出最值即可. 解答:解(1)解方程 x2﹣2x﹣3=0, 得 x1=3,x2=﹣1. ∵m<n, ∴m=﹣1,n=3…(1 分) ∴A(﹣1,﹣1),B(3,﹣3). ∵抛物线过原点,设抛物线的解析式为 y=ax2+bx. ∴ 解得: , ∴抛物线的解析式为 .…(4 分) (2)①设直线 AB 的解析式为 y=kx+b. ∴ 解得: , ∴直线 AB 的解析式为 . ∴C 点坐标为(0, ).…(6 分) ∵直线 OB 过点 O(0,0),B(3,﹣3), ∴直线 OB 的解析式为 y=﹣x. ∵△OPC 为等腰三角形, ∴OC=OP 或 OP=PC 或 OC=PC. 设 P(x,﹣x), (i)当 OC=OP 时, . 解得 , (舍去). ∴P1( , ). (ii)当 OP=PC 时,点 P 在线段 OC 的中垂线上, ∴P2( ,﹣ ). (iii)当 OC=PC 时,由 , 解得 ,x2=0(舍去). ∴P3( ,﹣ ). ∴P 点坐标为 P1( , )或 P2( ,﹣ )或 P3( ,﹣ ).…(9 分) ②过点 D 作 DG⊥x 轴,垂足为 G,交 OB 于 Q,过 B 作 BH⊥x 轴,垂足为 H. 设 Q(x,﹣x),D(x, ). S△BOD=S△ODQ+S△BDQ= DQ•OG+ DQ•GH, = DQ(OG+GH), = , = , ∵0<x<3, ∴当 时,S 取得最大值为 ,此时 D( ,﹣ ).…(13 分) 点评:此题主要考查了二次函数的综合应用以及等腰三角形的性质和三角形面积求法等知 识,求面积最值经常利用二次函数的最值求法得出. 【15. 2012 衢州】 24.如图,把两个全等的 Rt△AOB 和 Rt△COD 分别置于平面直角坐标系中,使直角边 OB、 OD 在 x 轴上.已知点 A(1,2),过 A、C 两点的直线分别交 x 轴、y 轴于点 E、F.抛物 线 y=ax2+bx+c 经过 O、A、C 三点. (1)求该抛物线的函数解析式 (2)点 P 为线段 OC 上一个动点,过点 P 作 y 轴的平行线交抛物线于点 M,交 x 轴于点 N, 问是否存在这样的点 P,使得四边形 ABPM 为等腰梯形?若存在,求出此时点 P 的坐标; 若不存在,请说明理由. (3)若△AOB 沿 AC 方向平移(点 A 始终在线段 AC 上,且不与点 C 重合),△AOB 在平 移过程中与△COD 重叠部分面积记为 S.试探究 S 是否存在最大值?若存在,求出这个最大 值;若不存在,请说明理由. 考点:二次函数综合题。 分析:(1)抛物线 y=ax2+bx+c 经过点 O、A、C,利用待定系数法求抛物线的解析式; (2)根据等腰梯形的性质,确定相关点的坐标以及线段长度的数量关系,得到一元 二次方程,求出 t 的值,从而可解.结论:存在点 P( , ),使得四边形 ABPM 为 等腰梯形; (3)本问关键是求得重叠部分面积 S 的表达式,然后利用二次函数的极值求得 S 的 最大值.解答中提供了三种求解面积 S 表达式的方法,殊途同归,可仔细体味. 解答:解:(1)∵抛物线 y=ax2+bx+c 经过点 O、A、C, 可得 c=0,∴ , 解得 a= ,b= , ∴抛物线解析式为 y= x2+ x. (2)设点 P 的横坐标为 t,∵PN∥CD,∴△OPN∽△OCD,可得 PN= ∴P(t, ),∵点 M 在抛物线上,∴M(t, t2+ t). 如解答图 1,过 M 点作 MG⊥AB 于 G,过 P 点作 PH⊥AB 于 H, AG=yA﹣yM=2﹣( t2+ t)= t2﹣ t+2,BH=PN= . 当 AG=BH 时,四边形 ABPM 为等腰梯形, ∴ t2﹣ t+2= , 化简得 3t2﹣8t+4=0,解得 t1=2(不合题意,舍去),t2= , ∴点 P 的坐标为( , ) ∴存在点 P( , ),使得四边形 ABPM 为等腰梯形. (3)如解答图 2,△AOB 沿 AC 方向平移至△A′O′B′,A′B′交 x 轴于 T,交 OC 于 Q, A′O′交 x 轴于 K,交 OC 于 R. 求得过 A、C 的直线为 yAC=﹣x+3,可设点 A′的横坐标为 a,则点 A′(a,﹣a+3), 易知△OQT∽△OCD,可得 QT= , ∴点 Q 的坐标为(a, ). 解法一: 设 AB 与 OC 相交于点 J, ∵△ARQ∽△AOJ,相似三角形对应高的比等于相似比,∴ = ∴HT= = =2﹣a, KT= A′T= (3﹣a),A′Q=yA′﹣yQ=(﹣a+3)﹣ =3﹣ a. S 四边形 RKTQ=S△A′KT﹣S△A′RQ= KT•A′T﹣ A′Q•HT = • •(3﹣a)﹣ •(3﹣ a)•(﹣a+2) = a2+ a﹣ = (a﹣ )2+ 由于 <0, ∴在线段 AC 上存在点 A′( , ),能使重叠部分面积 S 取到最大值,最大值为 . 解法二: 过点 R 作 RH⊥x 轴于 H,则由△ORH∽△OCD,得 ① 由△RKH∽△A′O′B′,得 ② 由①,②得 KH= OH, OK= OH,KT=OT﹣OK=a﹣ OH ③ 由△A′KT∽△A′O′B′,得 , 则 KT= ④ 由③,④得 =a﹣ OH,即 OH=2a﹣2,RH=a﹣1,所以点 R 的坐标为 R(2a ﹣2,a﹣1) S 四边形 RKTQ=S△QOT﹣S△ROK= •OT•QT﹣ •OK•RH = a• a﹣ (1+ a﹣ )•(a﹣1) = a2+ a﹣ = (a﹣ )2+ 由于 <0, ∴在线段 AC 上存在点 A′( , ),能使重叠部分面积 S 取到最大值,最大值为 . 解法三: ∵AB=2,OB=1,∴tan∠O′A′B′=tan∠OAB= , ∴KT=A′T•tan∠O′A′B′=(﹣a+3)• = a+ , ∴OK=OT﹣KT=a﹣( a+ )= a﹣ , 过点 R 作 RH⊥x 轴于 H,∵tan∠OAB=tan∠RKH= =2,∴RH=2KH 又∵tan∠OAB=tan∠ROH= = = , ∴2RH=OK+KH= a﹣ + RH,∴RH=a﹣1,OH=2(a﹣1), ∴点 R 坐标 R(2a﹣2,a﹣1) S 四边形 RKTQ=S△A′KT﹣S△A′RQ= •KT•A′T﹣ A′Q•(xQ﹣xR) = • •(3﹣a)﹣ •(3﹣ a)•(﹣a+2) = a2+ a﹣ = (a﹣ )2+ 由于 <0, ∴在线段 AC 上存在点 A′( , ),能使重叠部分面积 S 取到最大值,最大值为 . 点评:本题综合考查了二次函数的图象与性质、待定系数法、二次函数的最值、等腰梯形、 相似三角形、图形的平移以及几何图形面积的求法,涉及到的知识点众多,难度较大, 对学生能力要求较高,有利于训练并提升学生解决复杂问题的能力. 【16. 2012 绍兴】 25.如图,矩形 OABC 的两边在坐标轴上,连接 AC,抛物线 2 4 2y x x 经过 A,B 两 点。 (1)求 A 点坐标及线段 AB 的长; (2)若点 P 由点 A 出发以每秒 1 个单位的速度沿 AB 边向点 B 移动,1 秒后点 Q 也由点 A 出发以每秒 7 个单位的速度沿 AO,OC,CB 边向点 B 移动,当其中一个点到达终点时另一 个点也停止移动,点 P 的移动时间为 t 秒。 ①当 PQ⊥AC 时,求 t 的值; ②当 PQ∥AC 时,对于抛物线对称轴上一点 H,∠HOQ>∠POQ,求点 H 的纵坐标的取值 范围。 考点:二次函数综合题。 解答:解:(1)由抛物线 2 4 2y x x 知:当 x=0 时,y=﹣2, ∴A(0,﹣2)。 由于四边形 OABC 是矩形,所以 AB∥x 轴,即 A、B 的纵坐标相同; 当 2y 时, 22 4 2x x ,解得 1 20 4x x , , ∴B(4,﹣2), ∴AB=4。 (2)①由题意知:A 点移动路程为 AP=t, Q 点移动路程为 7( 1) 7 7t t 。 当 Q 点在 OA 上时,即 0 7 7 2t , 91 7t 时, 如图 1,若 PQ⊥AC,则有 Rt△QAP∽Rt△ABC。 ∴ QA AP=AB BC ,即 7 7 4 2 t t , ∴ 7 5t 。 ∵ 7 9 5 7 , ∴此时 t 值不合题意。 当 Q 点在 OC 上时,即 2 7 7 6t , 9 7 13 7t 时, 如图 2,过 Q 点作 QD⊥AB。 ∴AD=OQ=7(t﹣1)﹣2=7t﹣9。 ∴DP=t﹣(7t﹣9)=9﹣6t。 若 PQ⊥AC,则有 Rt△QDP∽Rt△ABC, ∴ QA DP=AB BC ,即 2 9 6 4 4 t , ∴ 4 3t 。 ∵ 9 4 13 7 3 7 , ∴ 4 3t 符合题意。 当 Q 点在 BC 上时,即 6 7 7 8t , 3 1 7 7 1 5t 时, 如图 3,若 PQ⊥AC,过 Q 点作 QG∥AC, 则 QG⊥PG,即∠GQP=90°。 ∴∠QPB>90°,这与△QPB 的内角和为 180°矛盾, 此时 PQ 不与 AC 垂直。 综上所述,当 4 3t 时,有 PQ⊥AC。 ②当 PQ∥AC 时,如图 4,△BPQ∽△BAC, ∴ BP BQ=BA BC , ∴ 4 8 7( 1) 4 2 t t , 解得 t=2,即当 t=2 时,PQ∥AC。 此时 AP=2,BQ=CQ=1, ∴P(2,﹣2),Q(4,﹣1)。 抛物线对称轴的解析式为 x=2, 当 H1 为对称轴与 OP 的交点时, 有∠H1OQ=∠POQ, ∴当 yH<﹣2 时,∠HOQ>∠POQ。 作 P 点关于 OQ 的对称点 P′,连接 PP′交 OQ 于点 M, 过 P′作 P′N 垂直于对称轴,垂足为 N,连接 OP′, 在 Rt△OCQ 中,∵OC=4,CQ=1。 ∴OQ= 17 , ∵S△OPQ=S 四边形 ABCD﹣S△AOP﹣S△COQ﹣S△QBP=3= 1 2 OQ×PM, ∴PM= 6 17 17 , ∴PP′=2PM=12 17 17 , ∵NPP′=∠COQ。 ∴Rt△COQ∽△Rt△NPP′ ∴ ' ' CQ P N=OQ PP , ∴ ' 12P N 17 , 48PN 17 , ∴P′( 46 14 17 17 , ), ∴直线 OP′的解析式为 7 23y x , ∴OP′与 NP 的交点 H2(2, 14 23 )。 ∴当 H 14 23y 时,∠HOP>∠POQ。 综上所述,当 H 2y 或 H 14 23y 时,∠HOQ>∠POQ。 【17.2012 南充】 22.如图,⊙C 的内接⊿AOB 中,AB=AO=4,tan∠AOB= 4 3 ,抛物线 y=ax2+bx 经过点 A(4, 0)与点(-2,6) (1)求抛物线的函数解析式. (2)直线 m 与⊙C 相切于点 A 交 y 轴于点 D,动点 P 在线段 OB 上,从点 O 出发向点 B 运动;同时动点 Q 在线段 DA 上,从点 D 出发向点 A 运动,点 P 的速度为每秒 1 个单位长, 点 Q 的速度为每秒 2 个单位长,当 PQ⊥AD 时,求运动时间 t 的值 (3)点 R 在抛物线位于 x 轴下方部分的图象上,当⊿ROB 面积 最大时,求点 R 的坐标. 考点:二次函数综合题;解二元一次方程组;二次函数最值的 应用;三角函数和勾股定理的应用;待定系数法求二次函数解 析式。 专题:计算题;代数几何综合题。 分析:(1)点 A(4,0)与点(-2,6)代入抛物线 y=ax2+bx,得: 16a+4b=0 a= 2 1 4a-2b=6 解得: b= -2 从而求出解析式。 (2)先得到∠ OAD=∠AOB ,作 OF⊥AD 于 F,再算出 OF 的长,t 秒时,OP=t,DQ=2t, 若 PQ⊥AD 则 FQ=OP= t DF=DQ-FQ= t ⊿ODF 中,t=DF= 22 OFOD = 22 4.23 =1.8(秒) (3)先设出R(x, 2 1 x2-2x) ,作RG⊥y轴于G 作RH⊥OB于H交y轴于I,则RG= x OG= 2 1 x2+2x 再算出 IR、HI 的长,从而求出 RH 的长 5 2 ( x- 4 11 )2+ 40 121 当 x= 4 11 时,RH 最大。S⊿ROB 最大。这时: 2 1 x2-2x= 2 1 ×( 4 11 )2-2× 4 11 =- 32 55 ∴点 R( 4 11 ,- 32 55 ) 解答: (1)把点 A(4,0)与点(-2,6)代入抛 物线 y=ax2+bx,得: 16a+4b=0 a= 2 1 4a-2b=6 解得: b= -2 ∴抛物线的函数解析式为:y= 2 1 x2-2x (2)连 AC 交 OB 于 E ∵直线 m 切⊙C 于 A ∴AC⊥m,∵ 弦 AB=AO ∴ ⌒ AB= ⌒ AO ∴AC⊥OB ∴m∥OB ∴∠ OAD=∠AOB ∵OA=4 tan∠AOB= 4 3 ∴OD=OA·tan∠OAD=4× 4 3 =3 作 OF⊥AD 于 F OF=OA·sin∠OAD=4× 5 3 =2.4 t 秒时,OP=t,DQ=2t,若 PQ⊥AD 则 FQ=OP= t DF=DQ-FQ= t ⊿ODF 中,t=DF= 22 OFOD = 22 4.23 =1.8(秒) (3)令 R(x, 2 1 x2-2x) (0<x<4) 作 RG⊥y 轴于 G 作 RH⊥OB 于 H 交 y 轴于 I 【18. 2012 梅州】 23.如图,矩形 OABC 中,A(6,0)、C(0,2 )、D(0,3 ),射线 l 过点 D 且与 x 轴平行,点 P、Q 分别是 l 和 x 轴正半轴上动点,满足∠PQO=60°. (1)①点 B 的坐标是 (6,2 ) ;②∠CAO= 30 度;③当点 Q 与点 A 重合时, 点 P 的坐标为 (3,3 ) ;(直接写出答案) (2)设 OA 的中心为 N,PQ 与线段 AC 相交于点 M,是否存在点 P,使△AMN 为等腰三 角形?若存在,请直接写出点 P 的横坐标为 m;若不存在,请说明理由. (3)设点 P 的横坐标为 x,△OPQ 与矩形 OABC 的重叠部分的面积为 S,试求 S 与 x 的函 数关系式和相应的自变量 x 的取值范围. 考点:相似三角形的判定与性质;矩形的性质;梯形;解直角三角形。 专题:代数几何综合题。 分析:(1)①由四边形 OABC 是矩形,根据矩形的性质,即可求得点 B 的坐标;②由正切 函数,即可求得∠CAO 的度数,③由三角函数的性质,即可求得点 P 的坐标; (2)分别从 MN=AN,AM=AN 与 AM=MN 去分析求解即可求得答案; (3)分别从当 0≤x≤3 时,当 3<x≤5 时,当 5<x≤9 时,当 x>9 时去分析求解即 可求得答案. 解答:解:(1)①∵四边形 OABC 是矩形, ∴AB=OC,OA=BC, ∵A(6,0)、C(0,2 ), ∴点 B 的坐标为:(6,2 ); ②∵tan∠CAO= = = , ∴∠CAO=30°; ③如下图:当当点 Q 与点 A 重合时,过点 P 作 PE⊥OA 于 E, ∵∠PQO=60°,D(0,3 ), ∴PE=3 , ∴AE= =3, ∴OE=OA﹣AE=6﹣3=3, ∴点 P 的坐标为(3,3 ); 故答案为:①(6,2 ),②30,③(3,3 ); (2)情况①:MN=AN=3, 则∠AMN=∠MAN=30°, ∴∠MNO=60°, ∵∠PQO=60°, 即∠MQO=60°, ∴点 N 与 Q 重合, ∴点 P 与 D 重合, ∴此时 m=0, 情况②,如图 AM=AN,作 MJ⊥x 轴、PI⊥x 轴; MJ=MQ•sin60°=AQ•sin60°=(OA﹣IQ﹣OI)•sin60°= (3﹣m) = AM= AN= , 可得 (3﹣m)= , 解得:m=3﹣ , 情况③AM=NM,此时 M 的横坐标是 4.5, 过点 P 作 PK⊥OA 于 K,过点 M 作 MG⊥OA 于 G, ∴MG= , ∴QK= = =3,GQ= = , ∴KG=3﹣0.5=2.5,AG= AN=1.5, ∴OK=2, ∴m=2, (3)当 0≤x≤3 时, 如图,OI=x,IQ=PI•tan60°=3,OQ=OI+IQ=3+x; 由题意可知直线 l∥BC∥OA, 可得 , EF= (3+x), 此时重叠部分是梯形,其面积为: S 梯形= (EF+OQ)•OC= (3+x), 当 3<x≤5 时,S=S 梯形﹣S△HAQ=S 梯形﹣ AH•AQ= (3+x)﹣ (x﹣3)2, 当 5<x≤9 时,S= (BE+OA)•OC= (12﹣ x), 当 9<x 时,S= OA•AH= . 点评:此题考查了矩形的性质,相似三角形的判定与性质、等腰三角形的性质以及直角三角 形的性质等知识.此题综合性较强,难度较大,注意数形结合思想与分类讨论思想的 应用. 【19. 2012 扬州】 27.已知抛物线 y=ax2+bx+c 经过 A (-1,0)、B(3,0)、C(0,3)三点,直线 l 是抛物 线的对称轴. (1)求抛物线的函数关系式; (2)设点 P 是直线 l 上的一个动点,当△PAC 的周长最小时,求点 P 的坐标; (3)在直线 l 上是否存在点 M,使△MAC 为等腰三角形?若存在,直接写出所有符合条件的 点 M 的坐标;若不存在,请说明理由. 考点: 二次函数综合题。 专题: 综合题;分类讨论。 分析: (1)直接将 A、B、C 三点坐标代入抛物线的解析式中求出待定系数即可. (2)由图知:A、B 点关于抛物线的对称轴对称,那么根据抛物线的对称性以及两点之 间线段最短可知:若连接 BC,那么 BC 与直线 l 的交点即为符合条件的 P 点. (3)由于△MAC 的腰和底没有明确,因此要分三种情况来讨论:①MA=AC、②MA =MC、②AC=MC;可先设出 M 点的坐标,然后用 M 点纵坐标表示△MAC 的三边 长,再按上面的三种情况列式求解. 解答: 解:(1)将 A(-1,0)、B(3,0)、C(0,3)代入抛物线 y=ax2+bx+c 中,得: ,解得: ∴抛物线的解析式:y=-x2+2x+3. (2)连接 BC,直线 BC 与直线 l 的交点为 P; 设直线 BC 的解析式为 y=kx+b,将 B(3,0),C(0,3)代入上式,得: ,解得: ∴直线 BC 的函数关系式 y=-x+3; 当 x-1 时,y=2,即 P 的坐标(1,2). (3)抛物线的解析式为:x=- =1,设 M(1,m),已知 A(-1,0)、C(0,3),则: MA2=m2+4,MC2=m2-6m+10,AC2=10; ①若 MA=MC,则 MA2=MC2,得: m2+4=m2-6m+10,得:m=1; ②若 MA=AC,则 MA2=AC2,得: m2+4=10,得:m=± ; ③若 MC=AC,则 MC2=AC2,得: m2-6m+10=10,得:m=0,m=6; 当 m=6 时,M、A、C 三点共线,构不成三角形,不合题意,故舍去; 综上可知,符合条件的 M 点,且坐标为 M(1, )(1,- )(1,1)(1,0). 点评: 该二次函数综合题涉及了抛物线的性质及解析式的确定、等腰三角形的判定等知识, 在判定等腰三角形时,一定要根据不同的腰和底分类进行讨论,以免漏解. 【20. 2012 连云港】 26.如图,甲、乙两人分别从 A(1, )、B(6,0)两点同时出发,点 O 为坐标原点,甲沿 AO 方向、乙沿 BO 方向均以 4km/h 的速度行驶,th 后,甲到达 M 点,乙到达 N 点. (1)请说明甲、乙两人到达 O 点前,MN 与 AB 不可能平行. (2)当 t 为何值时,△OMN∽△OBA? (3)甲、乙两人之间的距离为 MN 的长,设 s=MN2,求 s 与 t 之间的函数关系式,并求甲、 乙两人之间距离的最小值. 考点: 相似三角形的性质;坐标与图形性质;二次函数的最值;勾股定理;解直角三角形。 分析: (1)用反证法说明.根据已知条件分别表示相关线段的长度,根据三角形相似得比例 式说明; (2)根据两个点到达 O 点的时间不同分段讨论解答; (3)在不同的时间段运用相似三角形的判定和性质分别求解析式,运用函数性质解答 问题. 解答: 解:(1)因为 A 坐标为(1, ), 所以 OA=2,∠AOB=60°. 因为 OM=2-4t,ON=6-4t, 当 = 时,解得 t=0, 即在甲、乙两人到达 O 点前,只有当 t=0 时,△OMN∽△OAB,所以 MN 与 AB 不 可能平行; (2)因为甲达到 O 点时间为 t= ,乙达到 O 点的时间为 t= = ,所以甲先到达 O 点,所以 t= 或 t= 时,O、M、N 三点不能连接成三角形, ①当 t< 时,如果△OMN∽△OAB,则有 = ,解得 t=2> ,所以, △OMN 不可能相似△OBA; ②当 <t< 时,∠MON>∠AOB,显然△OMN 不相似△OBA; ③当 t> 时, = ,解得 t=2> ,所以当 t=2 时,△OMN∽△OBA; (3)①当 t≤ 时,如图 1,过点 M 作 MH⊥x 轴,垂足为 H, 在 Rt△MOH 中,因为∠AOB=60°, 所以 MH=OMsin60°=(2-4t)× = (1-2t), OH=0Mcos60°=(2-4t)× =1-2t, 所以 NH=(6-4t)-(1-2t)=5-2t, 所以 s=[ (1-2t)]2+(5-2t)2=16t2-32t+28 ②当 <t≤ 时,如图 2,作 MH⊥x 轴,垂足为 H, 在 Rt△MNH 中,MH= (4t-2)= (2t-1),NH= (4t-2)+(6-4t)=5-2t, 所以 s=[ (1-2t)]2+(5-2t)2=16t2-32t+28 当 t> 时,同理可得 s=[ (1-2t)]2+(5-2t)2=16t2-32t+28, 综上所述,s=[ (1-2t)]2+(5-2t)2=16t2-32t+28. 因为 s=16t2-32t+28=16(t-1)2+12, 所以当 t=1 时,s 有最小值为 12,所以甲、乙两人距离最小值为 2 km. 点评: 此题综合考查了坐标与图形、相似三角形的判定与性质、分类讨论数学思想的应用 等知识点,难度较大. 【21.2012 上海】 24.如图,在平面直角坐标系中,二次函数 y=ax2+6x+c 的图象经过点 A(4,0)、B(﹣ 1,0),与 y 轴交于点 C,点 D 在线段 OC 上,OD=t,点 E 在第二象限,∠ADE=90°, tan∠DAE= ,EF⊥OD,垂足为 F. (1)求这个二次函数的解析式; (2)求线段 EF、OF 的长(用含 t 的代数式表示); (3)当∠ECA=∠OAC 时,求 t 的值. 考点:相似三角形的判定与性质;待定系数法求二次函数解析式;全等三角形的判定与性质; 勾股定理。 解答:解:(1)二次函数 y=ax2+6x+c 的图象经过点 A(4,0)、B(﹣1,0), ∴ ,解得 , ∴这个二次函数的解析式为:y=﹣2x2+6x+8; (2)∵∠EFD=∠EDA=90 ∴∠DEF+∠EDF=90°,∠EDF+∠ODA=90°,∴∠DEF=∠ODA ∴△EDF∽△DAO ∴ . ∵ , ∴ = , ∴ ,∴EF= t. 同理 , ∴DF=2,∴OF=t﹣2. (3)∵抛物线的解析式为:y=﹣2x2+6x+8, ∴C(0,8),OC=8. 如图,连接 EC、AC,过 A 作 EC 的垂线交 CE 于 G 点. ∵∠ECA=∠OAC,∴∠OAC=∠GCA(等角的余角相等); 在△CAG 与△OCA 中, , ∴△CAG≌△OCA,∴CG=4,AG=OC=8. 如图,过 E 点作 EM⊥x 轴于点 M,则在 Rt△AEM 中, ∴EM=OF=t﹣2,AM=OA+AM=OA+EF=4+ t, 由勾股定理得: ∵AE2=AM2+EM2= ; 在 Rt△AEG 中,由勾股定理得: ∴EG= = = ∵在 Rt△ECF 中,EF= t,CF=OC﹣OF=10﹣t,CE=CG+EG= +4 由勾股定理得:EF2+CF2=CE2, 即 , 解得 t1=10(不合题意,舍去),t2=6, ∴t=6. 【22. 2012 广东】 22.如图,抛物线 y= x2﹣ x﹣9 与 x 轴交于 A、B 两点,与 y 轴交于点 C,连接 BC、AC. (1)求 AB 和 OC 的长; (2)点 E 从点 A 出发,沿 x 轴向点 B 运动(点 E 与点 A、B 不重合),过点 E 作直线 l 平 行 BC,交 AC 于点 D.设 AE 的长为 m,△ADE 的面积为 s,求 s 关于 m 的函数关系式, 并写出自变量 m 的取值范围; (3)在(2)的条件下,连接 CE,求△CDE 面积的最大值;此时,求出以点 E 为圆心,与 BC 相切的圆的面积(结果保留π). 考点:二次函数综合题。 解答:解:(1)已知:抛物线 y= x2﹣ x﹣9; 当 x=0 时,y=﹣9,则:C(0,﹣9); 当 y=0 时, x2﹣ x﹣9=0,得:x1=﹣3,x2=6,则:A(﹣3,0)、B(6,0); ∴AB=9,OC=9. (2)∵ED∥BC, ∴△AED∽△ABC, ∴ =( )2,即: =( )2,得:s= m2(0<m<9). (3)S△AEC= AE•OC= m,S△AED=s= m2; 则:S△EDC=S△AEC﹣S△AED=﹣ m2+ m=﹣ (m﹣ )2+ ; ∴△CDE 的最大面积为 ,此时,AE=m= ,BE=AB﹣AE= . 过 E 作 EF⊥BC 于 F,则 Rt△BEF∽Rt△BCO,得: = ,即: = ∴EF= ; ∴以 E 点为圆心,与 BC 相切的圆的面积 S⊙E=π•EF2= . 【23. 2012 嘉兴】 24.在平面直角坐标系 xOy 中,点 P 是抛物线:y=x2 上的动点(点在第一象限内).连接 OP, 过点 0 作 OP 的垂线交抛物线于另一点 Q.连接 PQ,交 y 轴于点 M.作 PA 丄 x 轴于点 A, QB 丄 x 轴于点 B.设点 P 的横坐标为 m. (1)如图 1,当 m= 时, ①求线段 OP 的长和 tan∠POM 的值; ②在 y 轴上找一点 C,使△OCQ 是以 OQ 为腰的等腰三角形,求点 C 的坐标; (2)如图 2,连接 AM、BM,分别与 OP、OQ 相交于点 D、E. ①用含 m 的代数式表示点 Q 的坐标; ②求证:四边形 ODME 是矩形. 考点:二次函数综合题。 解答:解:(1)①把 x= 代入 y=x2,得 y=2,∴P( ,2),∴OP= ∵PA 丄 x 轴,∴PA∥MO.∴tan∠P0M=tan∠0PA= = . ②设 Q(n,n2),∵tan∠QOB=tan∠POM, ∴ .∴n= ∴Q( , ),∴OQ= . 当 OQ=OC 时,则 C1(0, ),C2(0, ); 当 OQ=CQ 时,则 C3(0,1). (2)①∵P(m,m2),设 Q(n,n2),∵△APO∽△BOQ,∴ ∴ ,得 n= ,∴Q( , ). ②设直线 PO 的解析式为:y=kx+b,把 P(m,m2)、Q( , )代入,得: 解得 b=1,∴M(0,1) ∵ ,∠QBO=∠MOA=90°, ∴△QBO∽△MOA ∴∠MAO=∠QOB, ∴QO∥MA 同理可证:EM∥OD 又∵∠EOD=90°, ∴四边形 ODME 是矩形. 【24. 2012 贵州安顺】 26.如图所示,在平面直角坐标系 xOy 中,矩形 OABC 的边长 OA、OC 分别为 12cm、 6cm,点 A、C 分别在 y 轴的负半轴和 x 轴的正半轴上,抛物线 y=ax2+bx+c 经过点 A、B, 且 18a+c=0. (1)求抛物线的解析式. (2)如果点 P 由点 A 开始沿 AB 边以 1cm/s 的速度向终点 B 移动,同时点 Q 由点 B 开始 沿 BC 边以 2cm/s 的速度向终点 C 移动. ①移动开始后第 t 秒时,设△PBQ 的面积为 S,试写出 S 与 t 之间的函数关系式,并写出 t 的取值范围. ②当 S 取得最大值时,在抛物线上是否存在点 R,使得以 P、B、Q、R 为顶点的四边形是 平行四边形?如果存在,求出 R 点的坐标;如果不存在,请说明理由. 考点:二次函数综合题。 解答:解:(1)设抛物线的解析式为 y=ax2+bx+c, 由题意知点 A(0,﹣12), 所以 c=﹣12, 又 18a+c=0, , ∵AB∥OC,且 AB=6, ∴抛物线的对称轴是 , ∴b=﹣4, 所以抛物线的解析式为 ; (2)① ,(0<t<6) ②当 t=3 时,S 取最大值为 9. 这时点 P 的坐标(3,﹣12), 点 Q 坐标(6,﹣6) 若以 P、B、Q、R 为顶点的四边形是平行四边形,有如下三种情况: (Ⅰ)当点 R 在 BQ 的左边,且在 PB 下方时,点 R 的坐标(3,﹣18),将(3,﹣18)代 入抛物线的解析式中,满足解析式,所以存在,点 R 的坐标就是(3,﹣18), (Ⅱ)当点 R 在 BQ 的左边,且在 PB 上方时,点 R 的坐标(3,﹣6),将(3,﹣6)代入 抛物线的解析式中,不满足解析式,所以点 R 不满足条件. (Ⅲ)当点 R 在 BQ 的右边,且在 PB 上方时,点 R 的坐标(9,﹣6),将(9,﹣6)代入 抛物线的解析式中,不满足解析式,所以点 R 不满足条件. 综上所述,点 R 坐标为(3,﹣18). 【25. 2012 资阳】 25.抛物线 的顶点在直线 y=x+3 上,过点 F(﹣2,2)的直线交该抛物线于 点 M、N 两点(点 M 在点 N 的左边),MA⊥x 轴于点 A,NB⊥x 轴于点 B. (1)先通过配方求抛物线的顶点坐标(坐标可用含 m 的代数式表示),再求 m 的值; (2)设点 N 的横坐标为 a,试用含 a 的代数式表示点 N 的纵坐标,并说明 NF=NB; (3)若射线 NM 交 x 轴于点 P,且 PA•PB= ,求点 M 的坐标. 考点: 二次函数综合题。 专题: 压轴题。 分析: (1)利用配方法将二次函数整理成顶点式即可,再利用点在直线上的性质得出答案 即可; (2)首先利用点 N 在抛物线上,得出 N 点坐标,再利用勾股定理得出 NF2=NC2+FC2,进而得出 NF2=NB2,即可得出答案; (3)求点 M 的坐标,需要先求出直线 PF 的解析式.首先由(2)的思路得出 MF=MA, 然后连接 AF、FB,通过证明△PFA∽△PBF,利用相关的比例线段将 PA•PB 的值转化 为 PF 的值,进而求出点 F 的坐标和直线 PF 的解析式,即可得解. 解答: 解:(1)y= x2+x+m= (x+2)2+(m﹣1) ∴顶点坐标为(﹣2,m﹣1) ∵顶点在直线 y=x+3 上, ∴﹣2+3=m﹣1, 得 m=2; (2)∵点 N 在抛物线上, ∴点 N 的纵坐标为: a2+a+2, 即点 N(a, a2+a+2) 过点 F 作 FC⊥NB 于点 C, 在 Rt△FCN 中,FC=a+2,NC=NB﹣CB= a2+a, ∴NF2=NC2+FC2=( a2+a)2+(a+2)2, =( a2+a)2+(a2+4a)+4, 而 NB2=( a2+a+2)2, =( a2+a)2+(a2+4a)+4 ∴NF2=NB2, NF=NB; (3)连接 AF、BF, 由 NF=NB,得∠NFB=∠NBF,由(2)的结论知,MF=MA, ∴∠MAF=∠MFA, ∵MA⊥x 轴,NB⊥x 轴, ∴MA∥NB,∴∠AMF+∠BNF=180° ∵△MAF 和△NFB 的内角总和为 360°, ∴2∠MAF+2∠NBF=180°,∠MAF+∠NBF=90°, ∵∠MAB+∠NBA=180°, ∴∠FBA+∠FAB=90°, 又∵∠FAB+∠MAF=90°, ∴∠FBA=∠MAF=∠MFA, 又∵∠FPA=∠BPF, ∴△PFA∽△PBF, ∴ = ,PF2=PA×PB= , 过点 F 作 FG⊥x 轴于点 G,在 Rt△PFG 中, PG= = , ∴PO=PG+GO= , ∴P(﹣ ,0) 设直线 PF:y=kx+b,把点 F(﹣2,2)、点 P(﹣ ,0)代入 y=kx+b, 解得 k= ,b= , ∴直线 PF:y= x+ , 解方程 x2+x+2= x+ , 得 x=﹣3 或 x=2(不合题意,舍去), 当 x=﹣3 时,y= , ∴M(﹣3, ). 点评: 考查了二次函数综合题,在该二次函数综合题中,融入了勾股定理、相似三角形等 重点知识,(3)题通过构建相似三角形将 PA•PB 转化为 PF 的值是解题的关键,也 是该题的难点. 【26. 2012•德州】 23.如图所示,现有一张边长为 4 的正方形纸片 ABCD,点 P 为正方形 AD 边上的一点(不 与点 A、点 D 重合)将正方形纸片折叠,使点 B 落在 P 处,点 C 落在 G 处,PG 交 DC 于 H,折痕为 EF,连接 BP、BH. (1)求证:∠APB=∠BPH; (2)当点 P 在边 AD 上移动时,△PDH 的周长是否发生变化?并证明你的结论; (3)设 AP 为 x,四边形 EFGP 的面积为 S,求出 S 与 x 的函数关系式,试问 S 是否存在 最小值?若存在,求出这个最小值;若不存在,请说明理由. 考点: 翻折变换(折叠问题);二次函数的最值;全等三角形的判定与性质;正方形的性质。 分析: (1)根据翻折变换的性质得出∠PBC=∠BPH,进而利用平行线的性质得出∠APB= ∠PBC 即可得出答案; (2)首先证明△ABP≌△QBP,进而得出△BCH≌△BQH,即可得出 PD+DH+PH=AP+PD+DH+HC=AD+CD=8; (3)利用已知得出△EFM≌△BPA,进而利用在 Rt△APE 中,(4﹣BE)2+x2=BE2,利 用二次函数的最值求出即可. 解答: (1)解:如图 1,∵PE=BE, ∴∠EBP=∠EPB. 又∵∠EPH=∠EBC=90°, ∴∠EPH﹣∠EPB=∠EBC﹣∠EBP. 即∠PBC=∠BPH. 又∵AD∥BC, ∴∠APB=∠PBC. ∴∠APB=∠BPH. (2)△PHD 的周长不变为定值 8. 证明:如图 2,过 B 作 BQ⊥PH,垂足为 Q. 由(1)知∠APB=∠BPH, 又∵∠A=∠BQP=90°,BP=BP, ∴△ABP≌△QBP. ∴AP=QP,AB=BQ. 又∵AB=BC, ∴BC=BQ. 又∵∠C=∠BQH=90°,BH=BH, ∴△BCH≌△BQH. ∴CH=QH. ∴△PHD 的周长为:PD+DH+PH=AP+PD+DH+HC=AD+CD=8. (3)如图 3,过 F 作 FM⊥AB,垂足为 M,则 FM=BC=AB. 又∵EF 为折痕, ∴EF⊥BP. ∴∠EFM+∠MEF=∠ABP+∠BEF=90°, ∴∠EFM=∠ABP. 又∵∠A=∠EMF=90°, ∴△EFM≌△BPA. ∴EM=AP=x. ∴在 Rt△APE 中,(4﹣BE)2+x2=BE2. 解得, . ∴ . 又四边形 PEFG 与四边形 BEFC 全等, ∴ . 即: . 配方得, , ∴当 x=2 时,S 有最小值 6. 点评: 此题主要考查了翻折变换的性质以及全等三角形的判定与性质和勾股定理、二次函 数的最值问题等知识,熟练利用全等三角形的判定得出对应相等关系是解题关键. 【27. 2012 湘潭】 26.如图,抛物线 的图象与 x 轴交于 A、B 两点,与 y 轴交于 C 点,已知 B 点坐标为(4,0). (1)求抛物线的解析式; (2)试探究△ABC 的外接圆的圆心位置,并求出圆心坐标; (3)若点 M 是线段 BC 下方的抛物线上一点,求△MBC 的面积的最大值,并求出此时 M 点的坐标. 考点: 二次函数综合题。 专题: 转化思想。 分析: (1)该函数解析式只有一个待定系数,只需将 B 点坐标代入解析式中即可. (2)首先根据抛物线的解析式确定 A 点坐标,然后通过证明△ABC 是直角三角形来 推导出直径 AB 和圆心的位置,由此确定圆心坐标. (3)△MBC 的面积可由 S△MBC=BC×h 表示,若要它的面积最大,需要使 h 取最大 值,即点 M 到直线 BC 的距离最大,若设一条平行于 BC 的直线,那么当该直线与 抛物线有且只有一个交点时,该交点就是点 M. 解答: 解:(1)将 B(4,0)代入抛物线的解析式中,得: 0=16a﹣×4﹣2,即:a=; ∴抛物线的解析式为:y=x2﹣x﹣2. (2)由(1)的函数解析式可求得:A(﹣1,0)、C(0,﹣2); ∴OA=1,OC=2,OB=4, 即:OC2=OA•OB,又:OC⊥AB, ∴△OAC∽△OCB,得:∠OCA=∠OBC; ∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°, ∴△ABC 为直角三角形,AB 为△ABC 外接圆的直径; 所以该外接圆的圆心为 AB 的中点,且坐标为:(,0). (3)已求得:B(4,0)、C(0,﹣2),可得直线 BC 的解析式为:y=x﹣2; 设直线 l∥BC,则该直线的解析式可表示为:y=x+b,当直线 l 与抛物线只有一个交 点时,可列方程: x+b=x2﹣x﹣2,即: x2﹣2x﹣2﹣b=0,且△=0; ∴4﹣4×(﹣2﹣b)=0,即 b=4; ∴直线 l:y=x﹣4. 由于 S△MBC=BC×h,当 h 最大(即点 M 到直线 BC 的距离最远)时,△ABC 的面积 最大 所以点 M 即直线 l 和抛物线的唯一交点,有: , 解得: 即 M(2,﹣3). 点评: 考查了二次函数综合题,该题的难度不算太大,但用到的琐碎知识点较多,综合性 很强.熟练掌握直角三角形的相关性质以及三角形的面积公式是理出思路的关键. 【28. 2012 济宁】 23.如图,抛物线 y=ax2+bx﹣4 与 x 轴交于 A(4,0)、B(﹣2,0)两点,与 y 轴交于 点 C,点 P 是线段 AB 上一动点(端点除外),过点 P 作 PD∥AC,交 BC 于点 D,连接 CP. (1)求该抛物线的解析式; (2)当动点 P 运动到何处时,BP2=BD•BC; (3)当△PCD 的面积最大时,求点 P 的坐标. 考点: 二次函数综合题。 专题: 压轴题;转化思想。 分析: (1)该抛物线的解析式中有两个待定系数,只需将点 A、B 的坐标代入解析式中求 解即可. (2)首先设出点 P 的坐标,由 PD∥AC 得到△BPD∽△BAC,通过比例线段可表示出 BD 的长;BC 的长易得,根据题干给出的条件 BP2=BD•BC 即可求出点 P 的坐标. (3)由于 PD∥AC,根据相似三角形△BPD、△BAC 的面积比,可表示出△BPD 的面 积;以 BP 为底,OC 为高,易表示出△BPC 的面积,△BPC、△BPD 的面积差为△PDC 的面积,通过所列二次函数的性质,即可确定点 P 的坐标. 解答: 解:(1)由题意,得 , 解得 , ∴抛物线的解析式为 y= ﹣x﹣4; (2)设点 P 运动到点(x,0)时,有 BP2=BD•BC, 令 x=0 时,则 y=﹣4, ∴点 C 的坐标为(0,﹣4) ∵PD∥AC, ∴△BPD∽△BAC, ∴ . ∵BC= , AB=6,BP=x﹣(﹣2)=x+2. ∴BD= = = . ∵BP2=BD•BC, ∴(x+2)2= , 解得 x1= ,x2=﹣2(﹣2 不合题意,舍去), ∴点 P 的坐标是( ,0),即当点 P 运动到( ,0)时,BP2=BD•BC; (3)∵△BPD∽△BAC, ∴ , ∴ × S△BPC= ×(x+2)×4﹣ ∵ , ∴当 x=1 时,S△BPC 有最大值为 3. 即点 P 的坐标为(1,0)时,△PDC 的面积最大. 点评: 该题综合了相似三角形、图形面积的求法等知识,难度系数大,(3)题中,将所求 三角形的面积进行适当的转化是解题的关键所在. 【29. 2012 德阳】 24.在平面直角坐标 xOy 中,(如图)正方形 OABC 的边长为 4,边 OA 在 x 轴的正半轴 上,边 OC 在 y 轴的正半轴上,点 D 是 OC 的中点,BE⊥DB 交 x 轴于点 E. (1)求经过点 D、B、E 的抛物线的解析式; (2)将∠DBE 绕点 B 旋转一定的角度后,边 BE 交线段 OA 于点 F,边 BD 交 y 轴于点 G, 交(1)中的抛物线于 M(不与点 B 重合),如果点 M 的横坐标为 ,那么结论 OF= DG 能成立吗?请说明理由; (3)过(2)中的点 F 的直线交射线 CB 于点 P,交(1)中的抛物线在第一象限的部分于 点 Q,且使△PFE 为等腰三角形,求 Q 点的坐标. 考点: 二次函数综合题。 分析: (1)本题关键是求得 E 点坐标,然后利用待定系数法求抛物线解析式.如题图,可 以证明△BCD≌△BAE,则 AE=CD,从而得到 E 点坐标; (2)首先求出 M 点坐标,然后利用待定系数法求直线 MB 的解析式,令 x=0,求 得 G 点坐标,进而得到线段 CG、DG 的长度;由△BCG≌△BAF,可得 AF=CG,从 而求得 OF 的长度.比较 OF 与 DG 的长度,它们满足 OF= DG 的关系,所以结论 成立; (3)本问关键在于分类讨论.△PFE 为等腰三角形,如解答图所示,可能有三种情 况,需逐一讨论并求解. 解答: 解:(1)∵BE⊥DB 交 x 轴于点 E,OABC 是正方形, ∴∠DBC=EBA. 在△BCD 与△BAE 中, ∵ , ∴△BCD≌△BAE,∴AE=CD. ∵OABC 是正方形,OA=4,D 是 OC 的中点, ∴A(4,0),B(4,4),C(0,4),D(0,2),∴E(6,0). 设过点 D(0,2),B(4,4),E(6,0)的抛物线解析式为 y=ax2+bx+c,则有: , 解得 , ∴经过点 D、B、E 的抛物线的解析式为:y= x2+ x+2. (2)结论 OF= DG 能成立.理由如下: 由题意,当∠DBE 绕点 B 旋转一定的角度后,同理可证得△BCG≌△BAF,∴AF=CG. ∵xM= ,∴yM= xM 2+ xM+2= ,∴M( , ). 设直线 MB 的解析式为 yMB=kx+b, ∵M( , ),B(4,4), ∴ , 解得 , ∴yMB= x+6, ∴G(0,6), ∴CG=2,DG=4. ∴AF=CG=2,OF=OA﹣AF=2,F(2,0). ∵OF=2,DG=4, ∴结论 OF= DG 成立. (3)如图,△PFE 为等腰三角形,可能有三种情况,分类讨论如下: ①若 PF=FE. ∵FE=4,BC 与 OA 平行线之间距离为 4, ∴此时 P 点位于射线 CB 上, ∵F(2,0), ∴P(2,4),此时直线 FP⊥x 轴 ∴xQ=2, ∴yQ= xQ 2+ xQ+2= ,∴Q1(2, ); ②若 PF=PE. 如图所示,∵AF=AE=2,BA⊥FE, ∴△BEF 为等腰三角形, ∴此时点 P、Q 与点 B 重合, ∴Q2(4,4); ③若 PE=EF. ∵FE=4,BC 与 OA 平行线之间距离为 4, ∴此时 P 点位于射线 CB 上, ∵E(6,0),∴P(6,4). 设直线 yPF 的解析式为 yPF=kx+b,∵F(2,0),P(6,4), ∴ , 解得 , ∴yPF=x﹣2. ∵Q 点既在直线 PF 上,也在抛物线上, ∴ x2+ x+2=x﹣2,化简得 5x2﹣14x﹣48=0, 解得 x1= ,x2=﹣2(不合题意,舍去) ∴xQ=2, ∴yQ=xQ﹣2= ﹣2= . ∴Q3( , ). 综上所述,Q 点的坐标为 Q1(2, )或 Q2(4,4)或 Q3( , ). 点评: 本题是二次函数综合题,考查了二次函数的图象与性质、待定系数法求二次函数的 解析式、待定系数法求一次函数解析式、解一元二次方程、全等三角形的判定与性 质以及等腰三角形性质等知识点,考查内容涉及初中数学代数与几何的多个重要知 识点,难度较大.本题第(3)问需要针对等腰三角形△PFE 的三种可能情况进行分 类讨论,避免漏解. 【30. 2012 无锡】 26.如图 1,A.D 分别在 x 轴和 y 轴上,CD∥x 轴,BC∥y 轴.点 P 从 D 点出发,以 1cm/s 的速度,沿五边形 OABCD 的边匀速运动一周.记顺次连接 P、O、D 三点所围成图形的面 积为 Scm2,点 P 运动的时间为 ts.已知 S 与 t 之间的函数关系如图 2 中折线段 OEFGHI 所示. (1)求 A.B 两点的坐标; (2)若直线 PD 将五边形 OABCD 分成面积相等的两部分,求直线 PD 的函数关系式. 考点:动点问题的函数图象;一次函数综合题。 分析:(1)先连接 AD,设点 A 的坐标为(a,0),由图 2 得出 DO=6﹣AO 和 S△AOD=4, 即可得出 DO•AO=4,从而得出 a 的值,再根据图 2 得出 A 的坐标, 再延长 CB 交 x 轴于 M,根据 D 点的坐标得出 AB=5cm,CB=1cm,即可求出 AM= =4,从而得出点 B 的坐标. (2)先设点 P(x,y),连 PC.PO,得出 S 四边形 DPBC 的面积,再进行整理,即可得出 x 与 y 的关系,再由 A,B 点的坐标,求出直线 AB 的函数关系式,从而求出 x、y 的值,即 可得出 P 点的坐标,再设直线 PD 的函数关系式为 y=kx+4,求出 K 的值,即可得出直线 PD 的函数关系式. 解答:解:(1)连接 AD,设点 A 的坐标为(a,0), 由图 2 知,DO+OA=6cm, DO=6﹣AO, 由图 2 知 S△AOD=4, ∴ DO•AO=4, ∴a2﹣6a+8=0, 解得 a=2 或 a=4, 由图 2 知,DO>3, ∴AO<3, ∴a=2, ∴A 的坐标为(2,0), D 点坐标为(0,4), 在图 1 中,延长 CB 交 x 轴于 M, 由图 2,知 AB=5cm,CB=1cm, ∴MB=3, ∴AM= =4. ∴OM=6, ∴B 点坐标为(6,3); (2)显然点 P 一定在 AB 上.设点 P(x,y),连 PC.PO,则 S 四边形 DPBC=S△DPC+S△PBC= S 五边形 OABCD= (S 矩形 OMCD﹣S△ABM)=9, ∴ 6×(4﹣y)+ ×1×(6﹣x)=9, 即 x+6y=12, 同理,由 S 四边形 DPAO=9 可得 2x+y=9, 由 A(2,0),B(6,3)求得直线 AB 的函数关系式为 y= , 由 [或 或 ] 解得 x= ,y= . ∴P( , ), 设直线 PD 的函数关系式为 y=kx+4, 则 = k+4, ∴k=﹣ , ∴直线 PD 的函数关系式为 y=﹣ x+4. 点评:此题考查了动点问题的函数图象,解题的关键是根据题意设出函数关系式,是难点, 也是中考的重点,需熟练掌握. 【31.2012 临沂】 26.如图,点 A 在 x 轴上,OA=4,将线段 OA 绕点 O 顺时针旋转 120°至 OB 的位置. (1)求点 B 的坐标; (2)求经过点 A.O、B 的抛物线的解析式; (3)在此抛物线的对称轴上,是否存在点 P,使得以点 P、O、B 为顶点的三角形是等腰三 角形?若存在,求点 P 的坐标;若不存在,说明理由. 考点:二次函数综合题;分类讨论。 解答:解:(1)如图,过 B 点作 BC⊥x 轴,垂足为 C,则∠BCO=90°, ∵∠AOB=120°, ∴∠BOC=60°, 又∵OA=OB=4, ∴OC= OB= ×4=2,BC=OB•sin60°=4× =2 , ∴点 B 的坐标为(﹣2,﹣2 ); (2)∵抛物线过原点 O 和点 A.B, ∴可设抛物线解析式为 y=ax2+bx, 将 A(4,0),B(﹣2.﹣2 )代入,得 , 解得 , ∴此抛物线的解析式为 y=﹣ x2+ x (3)存在, 如图,抛物线的对称轴是 x=2,直线 x=2 与 x 轴的交点为 D,设点 P 的坐标为(2,y), ①若 OB=OP, 则 22+|y|2=42, 解得 y=±2 , 当 y=2 时,在 Rt△POD 中,∠PDO=90°,sin∠POD= = , ∴∠POD=60°, ∴∠POB=∠POD+∠AOB=60°+120°=180°, 即 P、O、B 三点在同一直线上, ∴y=2 不符合题意,舍去, ∴点 P 的坐标为(2,﹣2 ) ②若 OB=PB,则 42+|y+2 |2=42, 解得 y=﹣2 , 故点 P 的坐标为(2,﹣2 ), ③若 OP=BP,则 22+|y|2=42+|y+2 |2, 解得 y=﹣2 , 故点 P 的坐标为(2,﹣2 ), 综上所述,符合条件的点 P 只有一个,其坐标为(2,﹣2 ), 【32.2012 菏泽】 21.如图,在平面直角坐标系中放置一直角三角板,其顶点为 A(0,1),B(2,0),O(0, 0),将此三角板绕原点 O 逆时针旋转 90°,得到△A′B′O. (1)一抛物线经过点 A′、B′、B,求该抛物线的解析式; (2)设点 P 是在第一象限内抛物线上的一动点,是否存在点 P,使四边形 PB′A′B 的面积 是△A′B′O 面积 4 倍?若存在,请求出 P 的坐标;若不存在,请说明理由. (3)在(2)的条件下,试指出四边形 PB′A′B 是哪种形状的四边形?并写出四边形 PB′A′B 的两条性质. 考点:二次函数综合题。 解答:解:(1)△A′B′O 是由△ABO 绕原点 O 逆时针旋转 90°得到的, 又 A(0,1),B(2,0),O(0,0), ∴A′(﹣1,0),B′(0,2). 设抛物线的解析式为: 2 ( 0)y ax bx c a , ∵抛物线经过点 A′、B′、B, 0 2 0 4 2 a b c c a b c ,解之得 1 1 2 a b c , 满足条件的抛物线的解析式为 2 2y x x .. (2)∵P 为第一象限内抛物线上的一动点, 设 P(x,y),则 x>0,y>0,P 点坐标满足 2 2y x x . 连接 PB,PO,PB′, B OA B O OB PB A B S S S S P P四边形 1 1 11 2+ 2 + 22 2 2x y 2 2( 2) 1 2 3x x x x x . 假设四边形 PB A B 的面积是 A B O 面积的 4 倍,则 2 2 3 4x x , 即 2 2 1 0x x ,解之得 1x ,此时 21 1 2 2y ,即 (1,2)P . ∴存在点 P(1,2),使四边形 PB′A′B 的面积是△A′B′O 面积的 4 倍. (3)四边形 PB′A′B 为等腰梯形,答案不唯一,下面性质中的任意 2 个均可. ①等腰梯形同一底上的两个内角相等;②等腰梯形对角线相等; ③等腰梯形上底与下底平行;④等腰梯形两腰相等. 或用符号表示: ①∠B′A′B=∠PBA′或∠A′B′P=∠BPB′;②PA′=B′B;③B′P∥A′B;④B′A′=PB. 【33. 2012 义乌市】 24.如图 1,已知直线 y=kx 与抛物线 y= 交于点 A(3,6). (1)求直线 y=kx 的解析式和线段 OA 的长度; (2)点 P 为抛物线第一象限内的动点,过点 P 作直线 PM,交 x 轴于点 M(点 M、O 不 重合),交直线 OA 于点 Q,再过点 Q 作直线 PM 的垂线,交 y 轴于点 N.试探究:线段 QM 与线段 QN 的长度之比是否为定值?如果是,求出这个定值;如果不是,说明理由; (3)如图 2,若点 B 为抛物线上对称轴右侧的点,点 E 在线段 OA 上(与点 O、A 不重合), 点 D(m,0)是 x 轴正半轴上的动点,且满足∠BAE=∠BED=∠AOD.继续探究:m 在什 么范围时,符合条件的 E 点的个数分别是 1 个、2 个? 考点:二次函数综合题。 解答:解:(1)把点 A(3,6)代入 y=kx 得; ∵6=3k, ∴k=2, ∴y=2x.(2012 义乌市) OA= .…(3 分) (2) 是一个定值,理由如下: 如答图 1,过点 Q 作 QG⊥y 轴于点 G,QH⊥x 轴于点 H. ①当 QH 与 QM 重合时,显然 QG 与 QN 重合, 此时 ; ②当 QH 与 QM 不重合时, ∵QN⊥QM,QG⊥QH 不妨设点 H,G 分别在 x、y 轴的正半轴上, ∴∠MQH=∠GQN, 又∵∠QHM=∠QGN=90° ∴△QHM∽△QGN…(5 分), ∴ , 当点 P、Q 在抛物线和直线上不同位置时,同理可得 . …(7 分)①① (3)如答图 2,延长 AB 交 x 轴于点 F,过点 F 作 FC⊥OA 于点 C,过点 A 作 AR⊥x 轴于 点 R ∵∠AOD=∠BAE, ∴AF=OF, ∴OC=AC= OA= ∵∠ARO=∠FCO=90°,∠AOR=∠FOC, ∴△AOR∽△FOC, ∴ , ∴OF= , ∴点 F( ,0), 设点 B(x, ), 过点 B 作 BK⊥AR 于点 K,则△AKB∽△ARF, ∴ , 即 , 解得 x1=6,x2=3(舍去), ∴点 B(6,2), ∴BK=6﹣3=3,AK=6﹣2=4, ∴AB=5 …(8 分); (求 AB 也可采用下面的方法) 设直线 AF 为 y=kx+b(k≠0)把点 A(3,6),点 F( ,0)代入得 k= ,b=10, ∴ , ∴ , ∴ (舍去), , ∴B(6,2), ∴AB=5…(8 分) (其它方法求出 AB 的长酌情给分) 在△ABE 与△OED 中 ∵∠BAE=∠BED, ∴∠ABE+∠AEB=∠DEO+∠AEB, ∴∠ABE=∠DEO, ∵∠BAE=∠EOD, ∴△ABE∽△OED.…(9 分) 设 OE=x,则 AE= ﹣x ( ), 由△ABE∽△OED 得 , ∴ ∴ ( )…(10 分) ∴顶点为( , ) 如答图 3,当 时,OE=x= ,此时 E 点有 1 个; 当 时,任取一个 m 的值都对应着两个 x 值,此时 E 点有 2 个. ∴当 时,E 点只有 1 个…(11 分) 当 时,E 点有 2 个…(12 分). 【34.2012•杭州】 22.在平面直角坐标系内,反比例函数和二次函数 y=k(x2+x﹣1)的图象交于点 A(1,k) 和点 B(﹣1,﹣k). (1)当 k=﹣2 时,求反比例函数的解析式; (2)要使反比例函数和二次函数都是 y 随着 x 的增大而增大,求 k 应满足的条件以及 x 的 取值范围; (3)设二次函数的图象的顶点为 Q,当△ABQ 是以 AB 为斜边的直角三角形时,求 k 的值. 考点:二次函数综合题。 分析:(1)当 k=﹣2 时,即可求得点 A 的坐标,然后设反比例函数的解析式为:y= ,利 用待定系数法即可求得答案; (2)由反比例函数和二次函数都是 y 随着 x 的增大而增大,可得 k<0,又由二次函 数 y=k(x2+x﹣1)的对称轴为 x=﹣ ,可得 x<﹣ 时,才能使得 y 随着 x 的增大 而增大; (3)由△ABQ 是以 AB 为斜边的直角三角形,A 点与 B 点关于原点对称,利用直角 三角形斜边上的中线等于斜边的一半,即可得 OQ=OA=OB,又由 Q(﹣ , k), A(1,k),即可得 = ,继而求得答案. 解答:解:(1)当 k=﹣2 时,A(1,﹣2), ∵A 在反比例函数图象上, ∴设反比例函数的解析式为:y= , 代入 A(1,﹣2)得:﹣2= , 解得:m=﹣2, ∴反比例函数的解析式为:y=﹣ ; (2)∵要使反比例函数和二次函数都是 y 随着 x 的增大而增大, ∴k<0, ∵二次函数 y=k(x2+x﹣1)=k(x+ )2﹣ k,的对称轴为:直线 x=﹣ , 要使二次函数 y=k(x2+x﹣1)满足上述条件,在 k<0 的情况下,x 必须在对称轴的 左边, 即 x<﹣ 时,才能使得 y 随着 x 的增大而增大, ∴综上所述,k<0 且 x<﹣ ; (3)由(2)可得:Q(﹣ , k), ∵△ABQ 是以 AB 为斜边的直角三角形,A 点与 B 点关于原点对称,(如图是其中的一 种情况) ∴原点 O 平分 AB, ∴OQ=OA=OB, 作 AD⊥OC,QC⊥OC, ∴OQ= = , ∵OA= = , ∴ = , 解得:k=± . 点评:此题考查了二次函数的性质、反比例函数的性质以及直角三角形的性质等知识.此题 综合性较强,难度较大,注意掌握待定系数法求函数解析式,注意数形结合思想的应 用. 【35.2012 烟台】 26.如图,在平面直角坐标系中,已知矩形 ABCD 的三个顶点 B(1,0),C(3,0),D (3,4).以 A 为顶点的抛物线 y=ax2+bx+c 过点 C.动点 P 从点 A 出发,沿线段 AB 向 点 B 运动.同时动点 Q 从点 C 出发,沿线段 CD 向点 D 运动.点 P,Q 的运动速度均为每 秒 1 个单位.运动时间为 t 秒.过点 P 作 PE⊥AB 交 AC 于点 E. (1)直接写出点 A 的坐标,并求出抛物线的解析式; (2)过点 E 作 EF⊥AD 于 F,交抛物线于点 G,当 t 为何值时,△ACG 的面积最大?最大 值为多少? (3)在动点 P,Q 运动的过程中,当 t 为何值时,在矩形 ABCD 内(包括边界)存在点 H, 使以 C,Q,E,H 为顶点的四边形为菱形?请直接写出 t 的值. 考点:二次函数综合题。 分析:(1)根据矩形的性质可以写出点 A 得到坐标;由顶点 A 的坐标可设该抛物线的顶点 式方程为 y=a(x﹣1)2+4,然后将点 C 的坐标代入,即可求得系数 a 的值(利用待 定系数法求抛物线的解析式); (2)利用待定系数法求得直线 AC 的方程 y=﹣2x+6;由图形与坐标变换可以求得 点 P 的坐标(1,4﹣t),据此可以求得点 E 的纵坐标,将其代入直线 AC 方程可以求 得点 E 或点 G 的横坐标;然后结合抛物线方程、图形与坐标变换可以求得 GE=4﹣ 、 点 A 到 GE 的距离为 ,C 到 GE 的距离为 2﹣ ;最后根据三角形的面积公式可以求 得 S△ACG=S△AEG+S△CEG=﹣ (t﹣2)2+1,由二次函数的最值可以解得 t=2 时,S△ACG 的最大值为 1; (3)因为菱形是邻边相等的平行四边形,所以点 H 在直线 EF 上. 解答:解:(1)A(1,4).…(1 分) 由题意知,可设抛物线解析式为 y=a(x﹣1)2+4 ∵抛物线过点 C(3,0), ∴0=a(3﹣1)2+4, 解得,a=﹣1, ∴抛物线的解析式为 y=﹣(x﹣1)2+4,即 y=﹣x2+2x+3.…(2 分) (2)∵A(1,4),C(3,0), ∴可求直线 AC 的解析式为 y=﹣2x+6. ∵点 P(1,4﹣t).…(3 分) ∴将 y=4﹣t 代入 y=﹣2x+6 中,解得点 E 的横坐标为 x=1+ .…(4 分)∴点 G 的 横坐标为 1+ ,代入抛物线的解析式中,可求点 G 的纵坐标为 4﹣ . ∴GE=(4﹣ )﹣(4﹣t)=t﹣ .…(5 分) 又点 A 到 GE 的距离为 ,C 到 GE 的距离为 2﹣ , 即 S△ACG=S△AEG+S△CEG= •EG• + •EG(2﹣ ) = •2(t﹣ )=﹣ (t﹣2)2+1.…(7 分) 当 t=2 时,S△ACG 的最大值为 1.…(8 分) (3)t= 或 t=20﹣8 .…(12 分) (说明:每值各占(2 分),多出的值未舍去,每个扣 1 分) 点评:本题考查了二次函数的综合题.其中涉及到的知识点有待定系数法求二次函数的解析 式,待定系数法求一次函数的解析式以及三角形面积的求法. 【36.2012 益阳】 20.已知:如图,抛物线 y=a(x﹣1)2+c 与 x 轴交于点 A( ,0)和点 B,将抛物 线沿 x 轴向上翻折,顶点 P 落在点 P'(1,3)处. (1)求原抛物线的解析式; (2)学校举行班徽设计比赛,九年级 5 班的小明在解答此题时顿生灵感:过点 P'作 x 轴的 平行线交抛物线于 C、D 两点,将翻折后得到的新图象在直线 CD 以上的部分去掉,设计成 一个“W”型的班徽,“5”的拼音开头字母为 W,“W”图案似大鹏展翅,寓意深远;而 且小明通过计算惊奇的发现这个“W”图案的高与宽(CD)的比非常接近黄金分割比 (约等于 0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据: , ,结果可保留根号) 考点:二次函数的应用。 分析:(1)利用 P 与 P′(1,3)关于 x 轴对称,得出 P 点坐标,利用待定系数法求出二次 函数的解析式即可; (2)根据已知得出 C,D 两点坐标,进而得出“W”图案的高与宽(CD)的比. 解答:解:(1)∵P 与 P′(1,3)关于 x 轴对称, ∴P 点坐标为(1,﹣3); …(2 分) ∵抛物线 y=a(x﹣1)2+c 过点 A( ,0),顶点是 P(1,﹣3), ∴ ;…(3 分) 解得 ;…(4 分) 则抛物线的解析式为 y=(x﹣1)2﹣3,…(5 分) 即 y=x2﹣2x﹣2. (2)∵CD 平行 x 轴,P′(1,3)在 CD 上, ∴C、D 两点纵坐标为 3; …(6 分) 由(x﹣1)2﹣3=3, 解得: , ,…(7 分) ∴C、D 两点的坐标分别为( ,3),( ,3) ∴CD= …(8 分) ∴“W”图案的高与宽(CD)的比= (或约等于 0.6124)…(10 分). 点评:此题主要考查了待定系数法求二次函数的解析式以及二次函数的应用,根据已知得出 C,D 两点坐标是解题关键. 【37.2012 广州】 24.如图,抛物线 y= 与 x 轴交于 A、B 两点(点 A 在点 B 的左侧),与 y 轴交于点 C. (1)求点 A、B 的坐标; (2)设 D 为已知抛物线的对称轴上的任意一点,当△ACD 的面积等于△ACB 的面积时,求 点 D 的坐标; (3)若直线 l 过点 E(4,0),M 为直线 l 上的动点,当以 A、B、M 为顶点所作的直角三 角形有且只有三个时,求直线 l 的解析式. 考点:二次函数综合题。 分析:(1)A、B 点为抛物线与 x 轴交点,令 y=0,解一元二次方程即可求解. (2)根据题意求出△ACD 中 AC 边上的高,设为 h.在坐标平面内,作 AC 的平行线, 平行线之间的距离等于 h.根据等底等高面积相等的原理,则平行线与坐标轴的交点 即为所求的 D 点. 从一次函数的观点来看,这样的平行线可以看做是直线 AC 向上或向下平移而形成.因 此先求出直线 AC 的解析式,再求出平移距离,即可求得所作平行线的解析式,从而 求得 D 点坐标. 注意:这样的平行线有两条,如答图 1 所示. (3)本问关键是理解“以 A、B、M 为顶点所作的直角三角形有且只有三个”的含 义. 因为过 A、B 点作 x 轴的垂线,其与直线 l 的两个交点均可以与 A、B 点构成直角三 角形,这样已经有符合题意的两个直角三角形;第三个直角三角形从直线与圆的位置 关系方面考虑,以 AB 为直径作圆,当直线与圆相切时,根据圆周角定理,切点与 A、 B 点构成直角三角形.从而问题得解. 注意:这样的切线有两条,如答图 2 所示. 解答:解:(1)令 y=0,即 =0, 解得 x1=﹣4,x2=2, ∴A、B 点的坐标为 A(﹣4,0)、B(2,0). (2)S△ACB= AB•OC=9, 在 Rt△AOC 中,AC= = =5, 设△ACD 中 AC 边上的高为 h,则有 AC•h=9,解得 h= . 如答图 1,在坐标平面内作直线平行于 AC,且到 AC 的距离=h= ,这样的直线有 2 条,分别是 l1 和 l2,则直线与对称轴 x=﹣1 的两个交点即为所求的点 D. 设 l1 交 y 轴于 E,过 C 作 CF⊥l1 于 F,则 CF=h= , ∴CE= = . 设直线 AC 的解析式为 y=kx+b,将 A(﹣4,0),B(0,3)坐标代入, 得到 ,解得 ,∴直线 AC 解析式为 y= x+3. 直线 l1 可以看做直线 AC 向下平移 CE 长度单位( 个长度单位)而形成的, ∴直线 l1 的解析式为 y= x+3﹣ = x﹣ . 则 D1 的纵坐标为 ×(﹣1)﹣ = ,∴D1(﹣4, ). 同理,直线 AC 向上平移 个长度单位得到 l2,可求得 D2(﹣1, ) 综上所述,D 点坐标为:D1(﹣4, ),D2(﹣1, ). (3)如答图 2,以 AB 为直径作⊙F,圆心为 F.过 E 点作⊙F 的切线,这样的切线 有 2 条. 连接 FM,过 M 作 MN⊥x 轴于点 N. ∵A(﹣4,0),B(2,0),∴F(﹣1,0),⊙F 半径 FM=FB=3. 又 FE=5,则在 Rt△MEF 中, ME= =4,sin∠MFE= ,cos∠MFE= . 在 Rt△FMN 中,MN=MN•sin∠MFE=3× = , FN=MN•cos∠MFE=3× = ,则 ON= , ∴M 点坐标为( , ) 直线 l 过 M( , ),E(4,0), 设直线 l 的解析式为 y=kx+b,则有 ,解得 , 所以直线 l 的解析式为 y= x+3. 同理,可以求得另一条切线的解析式为 y= x﹣3. 综上所述,直线 l 的解析式为 y= x+3 或 y= x﹣3. 点评:本题解题关键是二次函数、一次函数以及圆等知识的综合运用.难点在于第(3)问 中对于“以 A、B、M 为顶点所作的直角三角形有且只有三个”条件的理解,这可以 从直线与圆的位置关系方面入手解决.本题难度较大,需要同学们对所学知识融会贯 通、灵活运用. 【38.2012 丽水】 24.在△ABC 中,∠ABC=45°,tan∠ACB= .如图,把△ABC 的一边 BC 放置在 x 轴上, 有 OB=14,OC= ,AC 与 y 轴交于点 E. (1)求 AC 所在直线的函数解析式; (2)过点 O 作 OG⊥AC,垂足为 G,求△OEG 的面积; (3)已知点 F(10,0),在△ABC 的边上取两点 P,Q,是否存在以 O,P,Q 为顶点的三角形 与△OFP 全等,且这两个三角形在 OP 的异侧?若存在,请求出所有符合条件的点 P 的坐标; 若不存在,请说明理由. 考点:一次函数综合题。 分析:(1)根据三角函数求 E 点坐标,运用待定系数法求解; (2)在 Rt△OGE 中,运用三角函数和勾股定理求 EG,OG 的长度,再计算面积; (3)分两种情况讨论求解:①点 Q 在 AC 上;②点 Q 在 AB 上.求直线 OP 与直线 AC 的交点坐标即可. 解答:解:(1)在 Rt△OCE 中,OE=OCtan∠OCE= = ,∴点 E(0,2 ). 设直线 AC 的函数解析式为 y=kx+ ,有 ,解得:k= . ∴直线 AC 的函数解析式为 y= . (2)在 Rt△OGE 中,tan∠EOG=tan∠OCE= = , 设 EG=3t,OG=5t,OE= = t,∴ ,得 t=2, 故 EG=6,OG=10, ∴S△OEG= . (3)存在. ①当点 Q 在 AC 上时,点 Q 即为点 G, 如图 1,作∠FOQ 的角平分线交 CE 于点 P1, 由△OP1F≌△OP1Q,则有 P1F⊥x 轴,由于点 P1 在直线 AC 上,当 x=10 时, y=- = , ∴点 P1(10, ). ②当点 Q 在 AB 上时, 如图 2,有 OQ=OF,作∠FOQ 的角平分线交 CE 于点 P2, 过点 Q 作 QH⊥OB 于点 H,设 OH=a, 则 BH=QH=14-a, 在 Rt△OQH 中,a2+(14-a)2=100, 解得:a1=6,a2=8, ∴Q(-6,8)或 Q(-8,6). 连接 QF 交 OP2 于点 M. 当 Q(-6,8)时,则点 M(2,4). 当 Q(-8,6)时,则点 M(1,3). 设直线 OP2 的解析式为 y=kx,则 2k=4,k=2. ∴y=2x. 解方程组 ,得 . ∴P2( ); 当 Q(-8,6)时,则点 M(1,3). 同理可求 P2′( ). 综上所述,满足条件的 P 点坐标为(10, )或( )或 ( ). 点评:此题考查一次函数的综合应用,运用了分类讨论的数学思想方法,综合性强,难度大. 【39. 2012 铜仁】 25.如图,已知:直线 3 xy 交 x 轴于点 A,交 y 轴于点 B,抛物线 y=ax2+bx+c 经 过 A、B、C(1,0)三点. (1)求抛物线的解析式; (2)若点 D 的坐标为(-1,0),在直线 3 xy 上有一点 P,使ΔABO 与ΔADP 相 似,求出点 P 的坐标; (3)在(2)的条件下,在 x 轴下方的抛物线上,是否存在点 E,使ΔADE 的面积等于 四边形 APCE 的面积?如果存在,请求出点 E 的坐标;如果不存在,请说明理由. 考点:二次函数综合题。 解答:解:(1):由题意得,A(3,0),B(0,3) ∵抛物线经过 A、B、C 三点,∴把 A(3,0),B(0,3),C(1,0)三点分别代入 2y ax bx c= + + 得方程组 0 3 039 cba c cba 解得: 3 4 1 c b a ∴抛物线的解析式为 2 4 3y x x= - + (2)由题意可得:△ABO 为等腰三角形,如图所示, 若△ABO∽△AP1D,则 1DP OB AD AO ∴DP1=AD=4 , ∴P1 ( 1,4)- 若△ABO∽△ADP2 ,过点 P2 作 P2 M⊥x 轴于 M,AD=4, ∵△ABO 为等腰三角形, ∴△ADP2 是等腰三角形,由三线合一可得:DM=AM=2= P2M,即点 M 与点 C 重合∴P2(1,2) (3)如图设点 E ( , )x y ,则 ||2||2 1 yyADS ADE ①当 P1(-1,4)时, S 四边形 AP1CE=S 三角形 ACP1+S 三角形 ACE ||22 1422 1 y = 4 y+ ∴ 2 4y y= + ∴ 4y = ∵点 E 在 x 轴下方 ∴ 4y = - 代入得: 2 4 3 4x x- + = - ,即 0742 xx ∵△=(-4)2-4×7=-12<0 ∴此方程无解 ②当 P2(1,2)时,S 四边形 AP2CE=S 三角形 ACP2+S 三角形 ACE = 2 y+ ∴ 2 2y y= + ∴ 2y = ∵点 E 在 x 轴下方 ∴ 2y = - 代入得: 2 4 3 2x x- + = - 即 0542 xx ,∵△=(-4)2-4×5=-4<0 ∴此方程无解 综上所述,在 x 轴下方的抛物线上不存在这样的点 E。 【40. 2012 泰安】 29.如图,半径为 2 的⊙C 与 x 轴的正半轴交于点 A,与 y 轴的正半轴交于点 B,点 C 的 坐标为(1,0).若抛物线 23 3y x bx c 过 A、B 两点. (1)求抛物线的解析式; (2)在抛物线上是否存在点 P,使得∠PBO=∠POB?若存在,求出点 P 的坐标;若不存在 说明理由; (3)若点 M 是抛物线(在第一象限内的部分)上一点,△MAB 的面积为 S,求 S 的最大 (小)值. 考点:二次函数综合题。 解答:解:(1)如答图 1,连接 OB. ∵BC=2,OC=1 ∴OB= 4 1 3 ∴B(0, 3 ) 将 A(3,0),B(0, 3 )代入二次函数的表达式 得 3 9 3 03 3 b c c ,解得: 2 3 3 3 b c , ∴ 23 2 3 33 3y x x . (2)存在. 如答图 2,作线段 OB 的垂直平分线 l,与抛物线的交点即为点 P. ∵B(0, 3 ),O(0,0), ∴直线 l 的表达式为 3 2y .代入抛物线的表达式, 得 23 2 3 333 3 2y x x ; 解得 101 2x , ∴P( 10 31 2 2 , ). (3)如答图 3,作 MH⊥x 轴于点 H. 设 M( m mx y, ), 则 S△MAB=S 梯形 MBOH+S△MHA﹣S△OAB= 1 2 (MH+OB)•OH+ 1 2 HA•MH﹣ 1 2 OA•OB = 1 1 1( 3) (3 ) 3 32 2 2m m m my x x y = 3 3 3 32 2 2m mx y ∵ 23 2 3 33 3m m my x x , ∴ 2 ΔMAB 3 3 3 2 3 3 3( 3)2 2 3 3 2m m mS x x x = 2 23 3 3 3 3 9 3( )2 2 2 2 8m m mx x x ∴当 3 2mx 时, ΔMABS 取得最大值,最大值为 9 3 8 . 【41.2012 长沙】 26.如图半径分别为 m,n(0<m<n)的两圆⊙O1 和⊙O2 相交于 P,Q 两点,且点 P(4, 1),两圆同时与两坐标轴相切,⊙O1 与 x 轴,y 轴分别切于点 M,点 N,⊙O2 与 x 轴,y 轴分别切于点 R,点 H. (1)求两圆的圆心 O1,O2 所在直线的解析式; (2)求两圆的圆心 O1,O2 之间的距离 d; (3)令四边形 PO1QO2 的面积为 S1,四边形 RMO1O2 的面积为 S2. 试探究:是否存在一条经过 P,Q 两点、开口向下,且在 x 轴上截得的线段长为 的抛物线?若存在,请求出此抛物线的解析式;若不存在,请说明理由. 解答: 解:(1)由题意可知 O1(m,m),O2(n,n), 设过点 O1,O2 的直线解析式为 y=kx+b,则有: (0<m<n),解得 , ∴所求直线的解析式为:y=x. (2)由相交两圆的性质,可知 P、Q 点关于 O1O2 对称. ∵P(4,1),直线 O1O2 解析式为 y=x,∴Q(1,4). 如解答图 1,连接 O1Q. ∵Q(1,4),O1(m,m),根据两点间距离公式得到: O1Q= = 又 O1Q 为小圆半径,即 QO1=m, ∴ =m,化简得:m2﹣10m+17=0 ① 如解答图 1,连接 O2Q,同理可得:n2﹣10n+17=0 ② 由①,②式可知,m、n 是一元二次方程 x2﹣10x+17=0 ③的两个根, 解③得:x=5± ,∵0<m<n,∴m=5﹣ ,n=5+ . ∵O1(m,m),O2(n,n), ∴d=O1O2= =8. (3)假设存在这样的抛物线,其解析式为 y=ax2+bx+c,因为开口向下,所以 a< 0. 如解答图 2,连接 PQ. 由相交两圆性质可知,PQ⊥O1O2. ∵P(4,1),Q(1,4), ∴PQ= = ,又 O1O2=8, ∴S1= PQ•O1O2= × ×8= ; 又 S2= (O2R+O1M)•MR= (n+m)(n﹣m)= ; ∴ = =1,即抛物线在 x 轴上截得的线段长为 1. ∵抛物线过点 P(4,1),Q(1,4), ∴ ,解得 , ∴抛物线解析式为:y=ax2﹣(5a+1)x+5+4a, 令 y=0,则有:ax2﹣(5a+1)x+5+4a=0, 设两根为 x1,x2,则有:x1+x2= ,x1x2= , ∵在 x 轴上截得的线段长为 1,即|x1﹣x2|=1, ∴(x1﹣x2)2=1,∴(x1+x2)2﹣4x1x2=1, 即( )2﹣4( )=1,化简得:8a2﹣10a+1=0, 解得 a= ,可见 a 的两个根均大于 0,这与抛物线开口向下(即 a<0)矛盾, ∴不存在这样的抛物线. 【42. 2012 六盘水】 25.如图 1,已知△ABC 中,AB=10cm,AC=8cm,BC=6cm.如果点 P 由 B 出发沿 BA 方向点 A 匀速运动,同时点 Q 由 A 出发沿 AC 方向向点 C 匀速运动,它们的速度均为 2cm/s.连接 PQ,设运动的时间为 t(单位:s)(0≤t≤4).解答下列问题: (1)当 t 为何值时,PQ∥BC. (2)设△AQP 面积为 S(单位:cm2),当 t 为何值时,S 取得最大值,并求出最大值. (3)是否存在某时刻 t,使线段 PQ 恰好把△ABC 的面积平分?若存在,求出此时 t 的值; 若不存在,请说明理由. (4)如图 2,把△AQP 沿 AP 翻折,得到四边形 AQPQ′.那么是否存在某时刻 t,使四边 形 AQPQ′为菱形?若存在,求出此时菱形的面积;若不存在,请说明理由. 考点:相似三角形的判定与性质;一元二次方程的应用;二次函数的最值;勾股定理;勾股 定理的逆定理;菱形的性质;翻折变换(折叠问题)。 专题:代数几何综合题;压轴题。 分析:(1)由 PQ∥BC 时的比例线段关系,列一元一次方程求解; (2)如解答图 1 所示,过 P 点作 PD⊥AC 于点 D,构造比例线段,求得 PD,从而可以得 到 S 的表达式,然后利用二次函数的极值求得 S 的最大值; (3)要点是利用(2)中求得的△AQP 的面积表达式,再由线段 PQ 恰好把△ABC 的面积平 分,列出一元二次方程;由于此一元二次方程的判别式小于 0,则可以得出结论:不存在这 样的某时刻 t,使线段 PQ 恰好把△ABC 的面积平分; (4)首先根据菱形的性质及相似三角形比例线段关系,求得 PQ、QD 和 PD 的长度;然后 在 Rt△PQD 中,求得时间 t 的值;最后求菱形的面积,值得注意的是菱形的面积等于△AQP 面积的 2 倍,从而可以利用(2)中△AQP 面积的表达式,这样可以化简计算. 解答:解:∵AB=10cm,AC=8cm,BC=6cm, ∴由勾股定理逆定理得△ABC 为直角三角形,∠C 为直角. (1)BP=2t,则 AP=10﹣2t. ∵PQ∥BC,∴ ,即 ,解得 t= , ∴当 t= s 时,PQ∥BC. (2)如答图 1 所示,过 P 点作 PD⊥AC 于点 D. ∴PD∥BC,∴ ,即 ,解得 PD=6﹣ t. S= ×AQ×PD= ×2t×(6﹣ t)=﹣ t2+6t=﹣ (t﹣ )2+ , ∴当 t= s 时,S 取得最大值,最大值为 cm2. (3)假设存在某时刻 t,使线段 PQ 恰好把△ABC 的面积平分, 则有 S△AQP= S△ABC,而 S△ABC= AC•BC=24,∴此时 S△AQP=12. 由(2)可知,S△AQP=﹣ t2+6t, ∴﹣ t2+6t=12,化简得:t2﹣5t+10=0, ∵△=(﹣5)2﹣4×1×10=﹣15<0,此方程无解, ∴不存在某时刻 t,使线段 PQ 恰好把△ABC 的面积平分. (4)假设存在时刻 t,使四边形 AQPQ′为菱形,则有 AQ=PQ=BP=2t. 如答图 2 所示,过 P 点作 PD⊥AC 于点 D,则有 PD∥BC, ∴ ,即 , 解得:PD=6﹣ t,AD=8﹣ t, ∴QD=AD﹣AQ=8﹣ t﹣2t=8﹣ t. 在 Rt△PQD 中,由勾股定理得:QD2+PD2=PQ2, 即(8﹣ t)2+(6﹣ t)2=(2t)2, 化简得:13t2﹣90t+125=0, 解得:t1=5,t2= , ∵t=5s 时,AQ=10cm>AC,不符合题意,舍去,∴t= . 由(2)可知,S△AQP=﹣ t2+6t ∴S 菱形 AQPQ′=2S△AQP=2×(﹣ t2+6t)=2×[﹣ ×( )2+6× ]= cm2. 所以存在时刻 t,使四边形 AQPQ′为菱形,此时菱形的面积为 cm2. 点评:本题是非常典型的动点型综合题,全面考查了相似三角形线段比例关系、菱形的性质、 勾股定理及其逆定理、一元一次方程的解法、一元二次方程的解法与判别式、二次函数的极 值等知识点,涉及的考点众多,计算量偏大,有一定的难度.本题考查知识点非常全面,是 一道测试学生综合能力的好题. 【43. 2012 攀枝花】 23.如图,在平面直角坐标系 xOy 中,四边形 ABCD 是菱形,顶点 A.C.D 均在坐标轴 上,且 AB=5,sinB= . (1)求过 A.C.D 三点的抛物线的解析式; (2)记直线 AB 的解析式为 y1=mx+n,(1)中抛物线的解析式为 y2=ax2+bx+c,求当 y1 <y2 时,自变量 x 的取值范围; (3)设直线 AB 与(1)中抛物线的另一个交点为 E,P 点为抛物线上 A.E 两点之间的一 个动点,当 P 点在何处时,△PAE 的面积最大?并求出面积的最大值. 考点:二次函数综合题。 专题:动点型。 分析:(1)由菱形 ABCD 的边长和一角的正弦值,可求出 OC.OD.OA 的长,进而确定 A.C.D 三点坐标,通过待定系数法可求出抛物线的解析式. (2)首先由 A.B 的坐标确定直线 AB 的解析式,然后求出直线 AB 与抛物线解析式的两 个交点,然后通过观察图象找出直线 y1 在抛物线 y2 图象下方的部分. (3)该题的关键点是确定点 P 的位置,△APE 的面积最大,那么 S△APE= AE×h 中 h 的值 最大,即点 P 离直线 AE 的距离最远,那么点 P 为与直线 AB 平行且与抛物线有且仅有的唯 一交点. 解答:解:(1)∵四边形 ABCD 是菱形, ∴AB=AD=CD=BC=5,sinB=sinD= ; Rt△OCD 中,OC=CD•sinD=4,OD=3; OA=AD﹣OD=2,即: A(﹣2,0)、B(﹣5,4)、C(0,4)、D(3,0); 设抛物线的解析式为:y=a(x+2)(x﹣3),得: 2×(﹣3)a=4,a=﹣ ; ∴抛物线:y=﹣ x2+ x+4. (2)由 A(﹣2,0)、B(﹣5,4)得直线 AB:y1=﹣ x﹣ ; 由(1)得:y2=﹣ x2+ x+4,则: , 解得: , ; 由图可知:当 y1<y2 时,﹣2<x<5. (3)∵S△APE= AE•h, ∴当 P 到直线 AB 的距离最远时,S△ABC 最大; 若设直线 L∥AB,则直线 L 与抛物线有且只有一个交点时,该交点为点 P; 设直线 L:y=﹣ x+b,当直线 L 与抛物线有且只有一个交点时, ﹣ x+b=﹣ x2+ x+4,且△=0; 求得:b= ,即直线 L:y=﹣ x+ ; 可得点 P( , ). 由(2)得:E(5,﹣ ),则直线 PE:y=﹣ x+9; 则点 F( ,0),AF=OA+OF= ; ∴△PAE 的最大值:S△PAE=S△PAF+S△AEF= × ×( + )= . 综上所述,当 P( , )时,△PAE 的面积最大,为 . 点评:该题考查的是函数的动点问题,其中综合了特殊四边形、图形面积的求法等知识,找 出动点问题中的关键点位置是解答此类问题的大致思路. 【44. 2012 山西】 26.综合与实践:如图,在平面直角坐标系中,抛物线 y=﹣x2+2x+3 与 x 轴交于 A.B 两 点,与 y 轴交于点 C,点 D 是该抛物线的顶点. (1)求直线 AC 的解析式及 B.D 两点的坐标; (2)点 P 是 x 轴上一个动点,过 P 作直线 l∥AC 交抛物线于点 Q,试探究:随着 P 点的运 动,在抛物线上是否存在点 Q,使以点 A.P、Q、C 为顶点的四边形是平行四边形?若存 在,请直接写出符合条件的点 Q 的坐标;若不存在,请说明理由. (3)请在直线 AC 上找一点 M,使△BDM 的周长最小,求出 M 点的坐标. 考点:二次函数综合题。 解答:解:(1)当 y=0 时,﹣x2+2x+3=0,解得 x1=﹣1,x2=3. ∵点 A 在点 B 的左侧, ∴A.B 的坐标分别为(﹣1,0),(3,0). 当 x=0 时,y=3. ∴C 点的坐标为(0,3) 设直线 AC 的解析式为 y=k1x+b1(k1≠0), 则 , 解得 , ∴直线 AC 的解析式为 y=3x+3. ∵y=﹣x2+2x+3=﹣(x﹣1)2+4, ∴顶点 D 的坐标为(1,4). (2)抛物线上有三个这样的点 Q, ①当点 Q 在 Q1 位置时,Q1 的纵坐标为 3,代入抛物线可得点 Q1 的坐标为(2,3); ②当点 Q 在点 Q2 位置时,点 Q2 的纵坐标为﹣3,代入抛物线可得点 Q2 坐标为(1+ , ﹣3); ③当点 Q 在 Q3 位置时,点 Q3 的纵坐标为﹣3,代入抛物线解析式可得,点 Q3 的坐标为 (1﹣ ,﹣3); 综上可得满足题意的点 Q 有三个,分别为:Q1(2,3),Q2(1+ ,﹣3),Q3(1﹣ , ﹣3). (3)点 B 作 BB′⊥AC 于点 F,使 B′F=BF,则 B′为点 B 关于直线 AC 的对称点.连接 B′D 交直线 AC 与点 M,则点 M 为所求, 过点 B′作 B′E⊥x 轴于点 E. ∵∠1 和∠2 都是∠3 的余角, ∴∠1=∠2. ∴Rt△AOC~Rt△AFB, ∴ , 由 A(﹣1,0),B(3,0),C(0,3)得 OA=1,OB=3,OC=3, ∴AC= ,AB=4. ∴ , ∴BF= , ∴BB′=2BF= , 由∠1=∠2 可得 Rt△AOC∽Rt△B′EB, ∴ , ∴ ,即 . ∴B′E= ,BE= , ∴OE=BE﹣OB= ﹣3= . ∴B′点的坐标为(﹣ , ). 设直线 B′D 的解析式为 y=k2x+b2(k2≠0). ∴ , 解得 , ∴直线 B'D 的解析式为:y= x+ , 联立 B'D 与 AC 的直线解析式可得: , 解得 , ∴M 点的坐标为( , ). 【45.2012 黄石】 25.(本小题满分 10 分)已知抛物线 1C 的函数解析式为 2 3 ( 0)y ax bx a b ,若抛物 线 1C 经过点 (0, 3) ,方程 2 3 0ax bx a 的两根为 1x , 2x ,且 1 2 4x x 。 (1)求抛物线 1C 的顶点坐标. (2)已知实数 0x ,请证明: 1x x ≥ 2 ,并说明 x 为何值时才会有 1 2x x . (3)若抛物线先向上平移 4 个单位,再向左平移 1 个单位后得到抛物线 2C ,设 1( , )A m y , 2( , )B n y 是 2C 上的两个不同点,且满足: 090AOB , 0m , 0n . 请你用含有 m 的表达式表示出△ AOB 的面积 S ,并求出 S 的最小值及 S 取最小值时一 次函数OA 的函数解析式。 (参考公式:在平面直角坐标系中,若 1 1( , )P x y , 2 2( , )Q x y ,则 P ,Q 两点间的距离 为 2 2 2 1 2 1( ) ( )x x y y ) 【考点】二次函数综合题. 【专题】压轴题;配方法. 【分析】(1)求抛物线的顶点坐标,需要先求出抛物线的解析式,即确定待定系数 a、 b 的值.已知抛物线图象与 y 轴交点,可确定解析式中的常数项(由此得 到 a 的值);然后从方程入手求 b 的值,题干给出了两根差的绝对值,将 其进行适当变形(转化为两根和、两根积的形式),结合根与系数的关系 即可求出 b 的值. (2) 1 1x x ,因此将 1x x 配成完全平方式,然后根据平方的非负性即可得 证. (3)结合(1)的抛物线的解析式以及函数的平移规律,可得出抛物线 C2 的解 析式;在 Rt△OAB 中,由勾股定理可确定 m、n 的关系式,然后用 m 列 出△AOB 的面积表达式,结合不等式的相关知识可确定△OAB 的最小面积 值以及此时 m 的值,进而由待定系数法确定一次函数 OA 的解析式. 【解答】解:(1)∵抛物线过(0,-3)点,∴-3a=-3 ∴a=1 ……………………………………1分 ∴y=x2+bx-3 ∵x2+bx-3=0的两根为 x1,x2 且 21 x-x =4 ∴ 21 2 2121 4)( xxxxxx =4且 b<0 ∴b=-2 ……………………1分 ∴y=x2-2x-3=(x-1)2-4 ∴抛物线C1的顶点坐标为(1,-4) ………………………1分 (2)∵x>0,∴ 0)1(21 x xxx ∴ ,21 xx 显然当 x=1时,才有 ,21 xx ………………………2分 (3)方法一:由平移知识易得C2的解析式为:y=x2 ………………………1分 ∴A(m,m2),B(n,n2) ∵ΔAOB 为 RtΔ ∴OA2+OB2=AB2 ∴m2+m4+n2+n4=(m-n)2+(m2-n2)2 化简得:m n=-1 ……………………1分 ∵SΔAOB= OBOA 2 1 = 4242 2 1 nnmm ∵m n=-1 ∴SΔAOB= 2 222 122 122 1 m mnm = 122 11 2 1)1(2 1 2 mmmm ∴SΔAOB 的最小值为1,此时 m=1,A(1,1) ……………………2分 ∴直线 OA 的一次函数解析式为y=x ……………………1分 方法二:由题意可求抛物线 2C 的解析式为: 2y x ································(1 分) ∴ 2( , )A m m , 2( , )B n n 过点 A 、 B 作 x 轴的垂线,垂足分别为 C 、 D ,则 AOC BODACDBS S S S 梯形 2 2 2 21 1 1( )( )2 2 2m n m n m m n n 1 ( )2 mn m n 由 BOD△ ∽ OAC△ 得 BD OD OC AC 即 2 2 n n m m ∴ 1mn ·············································································(1 分) ∴ 1n m ∴ 1 ( )2S mn m n 1 1( )2 m m 由(2)知: 1 2m m ∴ 1 1 1( ) 2 12 2S m m 当且仅当 1m , S 取得最小值 1 B(n,n2) A(m,m2) O CD y x 此时 A 的坐标为(1,1)······················································ (2 分) ∴一次函数OA的解析式为 y x ················································(1 分) 【点评】该题考查了二次函数解析式的确定、函数图象的平移、不等式的应用等知识, 解题过程中完全平方式的变形被多次提及,应熟练掌握并能灵活应用. 【46.2012 广安】 26.如图,在平面直角坐标系 xOy 中,AB⊥x 轴于点 B,AB=3,tan∠AOB= ,将△OAB 绕着原点 O 逆时针旋转 90°,得到△OA1B1;再将△OA1B1 绕着线段 OB1 的中点旋转 180°, 得到△OA2B1,抛物线 y=ax2+bx+c(a≠0)经过点 B、B1、A2. (1)求抛物线的解析式. (2)在第三象限内,抛物线上的点 P 在什么位置时,△PBB1 的面积最大?求出这时点 P 的 坐标. (3)在第三象限内,抛物线上是否存在点 Q,使点 Q 到线段 BB1 的距离为 ?若存在, 求出点 Q 的坐标;若不存在,请说明理由. 考点: 二次函数综合题。 分析: (1)首先根据旋转的性质确定点 B、B1、A2 三点的坐标,然后利用待定系数法求得 抛物线的解析式; (2)求出△PBB1 的面积表达式,这是一个关于 P 点横坐标的二次函数,利用二次函 数求极值的方法求出△PBB1 面积的最大值;值得注意的是求△PBB1 面积的方法,如 图 1 所示; (3)本问引用了(2)问中三角形面积表达式的结论,利用此表达式表示出△QBB1 的面积,然后解一元二次方程求得 Q 点的坐标. 解答: 解:(1)∵AB⊥x 轴,AB=3,tan∠AOB= ,∴OB=4, ∴B(﹣4,0),B1(0,﹣4),A2(3,0). ∵抛物线 y=ax2+bx+c(a≠0)经过点 B、B1、A2, ∴ , 解得 ∴抛物线的解析式为:y= x2+ x﹣4. (2)点 P 是第三象限内抛物线 y= x2+ x﹣4 上的一点, 如答图 1,过点 P 作 PC⊥x 轴于点 C. 设点 P 的坐标为(m,n),则 m<0,n<0,n= m2+ m﹣4. 于是 PC=|n|=﹣n=﹣ m2﹣ m﹣4,OC=|m|=﹣m,BC=OB﹣OC=|﹣4|﹣ |m|=4+m. S△PBB1=S△PBC+S 梯形 PB1OC﹣S△OBB1 = ×BC×PC+ ×(PC+OB1)×OC﹣ ×OB×OB1 = ×(4+m)×(﹣ m2﹣ m﹣4)+ ×[(﹣ m2﹣ m﹣4)+4]×(﹣m)﹣ ×4×4 = m2﹣ m= (m+2)2+ 当 m=﹣2 时,△PBB1 的面积最大,这时,n= ,即点 P(﹣2, ). (3)假设在第三象限的抛物线上存在点 Q(x0,y0),使点 Q 到线段 BB1 的距离为 . 如答图 2,过点 Q 作 QD⊥BB1 于点 D. 由(2)可知,此时△QBB1 的面积可以表示为: (x0+2)2+ , 在 Rt△OBB1 中,BB1= = ∵S△QBB1= ×BB1×QD= × × =2, ∴ (x0+2)2+ =2, 解得 x0=﹣1 或 x0=﹣3 当 x0=﹣1 时,y0=﹣4;当 x0=﹣3 时,y0=﹣2, 因此,在第三象限内,抛物线上存在点 Q,使点 Q 到线段 BB1 的距离为 ,这样 的点 Q 的坐标是(﹣1,﹣4)或(﹣3,﹣2). 点评: 本题综合考查了待定系数法求抛物线解析式、二次函数图象上点的坐标特征、一元 二次方程、旋转与坐标变化、图形面积求法、勾股定理等重要知识点.第(2)问起 承上启下的作用,是本题的难点与核心,其中的要点是坐标平面内图形面积的求解 方法,这种方法是压轴题中常见的一种解题方法,同学们需要认真掌握. 【47. 2012 张家界】 25.如图,抛物线 y=﹣x2+ x+2 与 x 轴交于 C.A 两点,与 y 轴交于点 B,OB=4.点 O 关于直线 AB 的对称点为 D,E 为线段 AB 的中点. (1)分别求出点 A.点 B 的坐标; (2)求直线 AB 的解析式; (3)若反比例函数 y= 的图象过点 D,求 k 值; (4)两动点 P、Q 同时从点 A 出发,分别沿 AB.AO 方向向 B.O 移动,点 P 每秒移动 1 个单位,点 Q 每秒移动 个单位,设△POQ 的面积为 S,移动时间为 t,问:S 是否存在最 大值?若存在,求出这个最大值,并求出此时的 t 值;若不存在,请说明理由. 考点:二次函数综合题。 解答:解:(1)令 y=0,即﹣x2+ x+2=0;解得 x1=﹣ ,x2=2 . ∴C(﹣ ,0)、A(2 ,0). 令 x=0,即 y=2, ∴B(0,2). 综上,A(2 ,0)、B(0,2). (2)令 AB 方程为 y=k1x+2 因为点 A(2 ,0)在直线上, ∴0=k12 +2 ∴k1=﹣ ∴直线 AB 的解析式为 y=﹣ x+2. (3)由 A(2 ,0)、B(0,2)得:OA=2 ,OB=2,AB=4,∠BAO=30°,∠DOA=60°; OD 与 O 点关于 AB 对称 ∴OD=OA=2 ∴D 点的横坐标为 ,纵坐标为 3,即 D( ,3). 因为 y= 过点 D, ∴3= ,∴k=3 . (4)AP=t,AQ= t,P 到 x 轴的距离:AP•sin30°= t,OQ=OA﹣AQ=2 ﹣ t; ∴S△OPQ= •(2 ﹣ t)• t=﹣ (t﹣2 )2+ ; 依题意, 得 0<t≤4 ∴当 t=2 时,S 有最大值为 . 【48. 2012 宜宾】 22.如图,抛物线 y=x2﹣2x+c 的顶点 A 在直线 l:y=x﹣5 上. (1)求抛物线顶点 A 的坐标; (2)设抛物线与 y 轴交于点 B,与 x 轴交于点 C.D(C 点在 D 点的左侧),试判断△ABD 的形状; (3)在直线 l 上是否存在一点 P,使以点 P、A.B.D 为顶点的四边形是平行四边形?若 存在,求点 P 的坐标;若不存在,请说明理由. 考点:二次函数综合题。 解答:解:(1)∵顶点 A 的横坐标为 x= =1,且顶点 A 在 y=x﹣5 上, ∴当 x=1 时,y=1﹣5=﹣4, ∴A(1,﹣4). (2)△ABD 是直角三角形. 将 A(1,﹣4)代入 y=x2﹣2x+c,可得,1﹣2+c=﹣4,∴c=﹣3, ∴y=x2﹣2x﹣3,∴B(0,﹣3) 当 y=0 时,x2﹣2x﹣3=0,x1=﹣1,x2=3 ∴C(﹣1,0),D(3,0), BD2=OB2+OD2=18,AB2=(4﹣3)2+12=2,AD2=(3﹣1)2+42=20, BD2+AB2=AD2, ∴∠ABD=90°,即△ABD 是直角三角形. (3)存在. 由题意知:直线 y=x﹣5 交 y 轴于点 A(0,﹣ 5),交 x 轴于点 F(5,0) ∴OE=OF=5,又∵OB=OD=3 ∴△OEF 与△OBD 都是等腰直角三角形 ∴BD∥l,即 PA∥BD 则构成平行四边形只能是 PADB 或 PABD,如图, 过点 P 作 y 轴的垂线,过点 A 作 x 轴的垂线并交于点 C 设 P(x1,x1﹣5),则 G(1,x1﹣5) 则 PC=|1﹣x1|,AG=|5﹣x1﹣4|=|1﹣x1| PA=BD=3 由勾股定理得: (1﹣x1)2+(1﹣x1)2=18,x1 2﹣2x1﹣8=0,x1=﹣2,4 ∴P(﹣2,﹣7),P(4,﹣1) 存在点 P(﹣2,﹣7)或 P(4,﹣1)使以点 A.B.D.P 为顶点的四边形是平行四边形. 【49. 2012 武汉】 25.如图 1,点 A 为抛物线 C1:y= x2﹣2 的顶点,点 B 的坐标为(1,0)直线 AB 交抛 物线 C1 于另一点 C (1)求点 C 的坐标; (2)如图 1,平行于 y 轴的直线 x=3 交直线 AB 于点 D,交抛物线 C1 于点 E,平行于 y 轴 的直线 x=a 交直线 AB 于 F,交抛物线 C1 于 G,若 FG:DE=4:3,求 a 的值; (3)如图 2,将抛物线 C1 向下平移 m(m>0)个单位得到抛物线 C2,且抛物线 C2 的顶 点为点 P,交 x 轴于点 M,交射线 BC 于点 N.NQ⊥x 轴于点 Q,当 NP 平分∠MNQ 时, 求 m 的值. 考点:二次函数综合题。 解答:解:(1)当 x=0 时,y=﹣2;∴A(0,﹣2). 设直线 AB 的解析式为 y=kx+b,则: ,解得 ∴直线 AB 解析式为 y=2x﹣2. ∵点 C 为直线 y=2x﹣2 与抛物线 y= x2﹣2 的交点,则点 C 的横、纵坐标满足: ,解得 、 (舍) ∴点 C 的坐标为(4,6). (2)直线 x=3 分别交直线 AB 和抛物线 C1 于 D.E 两点. ∴yD=4,yE= ,∴DE= . ∵FG=DE=4:3,∴FG=2. ∵直线 x=a 分别交直线 AB 和抛物线 C1 于 F、G 两点. ∴yF=2a﹣2,yG= a2﹣2 ∴FG=|2a﹣ a2|=2, 解得:a1=2,a2=﹣2+2 ,a3=2﹣2 . (3)设直线 MN 交 y 轴于 T,过点 N 做 NH⊥y 轴于点 H; 设点 M 的坐标为(t,0),抛物线 C2 的解析式为 y= x2﹣2﹣m; ∴0=﹣ t2﹣2﹣m,∴﹣2﹣m=﹣ t2. ∴y= x2﹣ t2,∴点 P 坐标为(0,﹣ t2). ∵点 N 是直线 AB 与抛物线 y= x2﹣ t2 的交点,则点 N 的横、纵坐标满足: ,解得 、 (舍) ∴N(2﹣t,2﹣2t). NQ=2﹣2t,MQ=2﹣2t, ∴MQ=NQ,∴∠MNQ=45°. ∴△MOT、△NHT 均为等腰直角三角形, ∴MO=OT,HT=HN ∴OT=4,NT=﹣ ,NH= (2﹣t),PT=﹣t+ t2. ∵PN 平分∠MNQ, ∴PT=NT, ∴﹣t+ t2= (2﹣t), ∴t1=﹣2 ,t2=2(舍) ﹣2﹣m=﹣ t2=﹣ (﹣2 )2,∴m=2. 【50.2012 潜江】 24.如图,抛物线 y=ax2+bx+2 交 x 轴于 A(﹣1,0),B(4,0)两点,交 y 轴于点 C, 与过点 C 且平行于 x 轴的直线交于另一点 D,点 P 是抛物线上一动点. (1)求抛物线解析式及点 D 坐标; (2)点 E 在 x 轴上,若以 A,E,D,P 为顶点的四边形是平行四边形,求此时点 P 的坐标; (3)过点 P 作直线 CD 的垂线,垂足为 Q,若将△CPQ 沿 CP 翻折,点 Q 的对应点为 Q′.是 否存在点 P,使 Q′恰好落在 x 轴上?若存在,求出此时点 P 的坐标;若不存在,说明理由. 考点: 二次函数综合题。 专题: 综合题。 分析: (1)用待定系数法可得出抛物线的解析式,令 y=2 可得出点 D 的坐标; (2)分两种情况进行讨论,①当 AE 为一边时,AE∥PD,②当 AE 为对角线时,根 据平行四边形对顶点到另一条对角线距离相等,求解点 P 坐标. (3)结合图形可判断出点 P 在直线 CD 下方,设点 P 的坐标为(a,﹣ a2+ a+2), 分情况讨论,①当 P 点在 y 轴右侧时,②当 P 点在 y 轴左侧时,运用解直角三角形 及相似三角形的性质进行求解即可. 解答: 解:(1)∵抛物线 y=ax2+bx+2 经过 A(﹣1,0),B(4,0)两点, ∴ , 解得: ∴y=﹣ x2+ x+2; 当 y=2 时,﹣ x2+ x+2=2,解得:x1=3,x2=0(舍), 即:点 D 坐标为(3,2). (2)A,E 两点都在 x 轴上,AE 有两种可能: ①当 AE 为一边时,AE∥PD, ∴P1(0,2), ②当 AE 为对角线时,根据平行四边形对顶点到另一条对角线距离相等, 可知 P 点、D 点到直线 AE(即 x 轴)的距离相等, ∴P 点的纵坐标为﹣2, 代入抛物线的解析式:﹣ x2+ x+2=﹣2 解得:x1= ,x2= , ∴P 点的坐标为( ,﹣2),( ,﹣2) 综上所述:p1(0,2);p2( ,﹣2);p3( ,﹣2). (3)存在满足条件的点 P,显然点 P 在直线 CD 下方,设直线 PQ 交 x 轴于 F,点 P 的坐标为(a,﹣ a2+ a+2), ①当 P 点在 y 轴右侧时(如图 1),CQ=a, PQ=2﹣(﹣ a2+ a+2)= a2﹣ a, 又∵∠CQ′O+∠FQ′P=90°,∠COQ′=∠Q′FP=90°, ∴∠FQ′P=∠OCQ′, ∴△COQ′~△Q′FP, , , ∴Q′F=a﹣3, ∴OQ′=OF﹣Q′F=a﹣(a﹣3)=3,CQ=CQ′= = , 此时 a= ,点 P 的坐标为( , ), ②当 P 点在 y 轴左侧时(如图 2)此时 a<0,,﹣ a2+ a+2<0,CQ=﹣a, PQ=2﹣(﹣ a2+ a+2)= a2﹣ a, 又∵∠CQ′O+∠FQ′P=90°,∠CQ′O+∠OCQ′=90°, ∴∠FQ′P=∠OCQ′,∠COQ′=∠Q′FP=90°, ∴△COQ′~△Q′FP, , ,Q′F=3﹣a, ∴OQ′=3, CQ=CQ′= , 此时 a=﹣ ,点 P 的坐标为(﹣ , ). 综上所述,满足条件的点 P 坐标为( , ),(﹣ , ). 点评: 此题考查了二次函数的综合应用,综合考查了翻折变换、相似三角形的判定与性质, 解答此类题目要求我们能将所学的知识融会贯通,属于中考常涉及的题目,同学们 一定要留意. 【51. 2012 娄底】 24.已知二次函数 y=x2﹣(m2﹣2)x﹣2m 的图象与 x 轴交于点 A(x1,0)和点 B(x2, 0),x1<x2,与 y 轴交于点 C,且满足 . (1)求这个二次函数的解析式; (2)探究:在直线 y=x+3 上是否存在一点 P,使四边形 PACB 为平行四边形?如果有, 求出点 P 的坐标;如果没有,请说明理由. 考点:二次函数综合题。 分析:(1)欲求抛物线的解析式,关键是求得 m 的值.根据题中所给关系式,利用一元二 次方程根与系数的关系,可以求得 m 的值,从而问题得到解决.注意:解答中求得两个 m 的值,需要进行检验,把不符合题意的 m 值舍去; (2)利用平行四边形的性质构造全等三角形,根据全等关系求得 P 点的纵坐标,进而得到 P 点的横坐标,从而求得 P 点坐标. 解答:解:(1)∵二次函数 y=x2﹣(m2﹣2)x﹣2m 的图象与 x 轴交于点 A(x1,0)和点 B(x2,0),x1<x2, 令 y=0,即 x2﹣(m2﹣2)x﹣2m=0 ①,则有: x1+x2=m2﹣2,x1x2=﹣2m. ∴ = = = , 化简得到:m2+m﹣2=0,解得 m1=﹣2,m2=1. 当 m=﹣2 时,方程①为:x2﹣2x+4=0,其判别式△=b2﹣4ac=﹣12<0,此时抛物线与 x 轴没有交点,不符合题意,舍去; 当 m=1 时,方程①为:x2+x﹣2=0,其判别式△=b2﹣4ac=9>0,此时抛物线与 x 轴有两 个不同的交点,符合题意. ∴m=1, ∴抛物线的解析式为 y=x2+x﹣2. (2)假设在直线 y=x+3 上是否存在一点 P,使四边形 PACB 为平行四边形. 如图所示,连接 PA.PB.AC.BC,过点 P 作 PD⊥x 轴于 D 点. ∵抛物线 y=x2+x﹣2 与 x 轴交于 A.B 两点,与 y 轴交于 C 点, ∴A(﹣2,0),B(1,0),C(0,2),∴OB=1,OC=2. ∵PACB 为平行四边形,∴PA∥BC,PA=BC, ∴∠PAD=∠CBO,∴∠APD=∠OCB. 在 Rt△PAD 与 Rt△CBO 中, ∵ , ∴Rt△PAD≌Rt△CBO, ∴PD=OC=2,即 yP=2, ∴直线解析式为 y=x+3, ∴xP=﹣1, ∴P(﹣1,2). 所以在直线 y=x+3 上存在一点 P,使四边形 PACB 为平行四边形,P 点坐标为(﹣1,2). 点评:本题是代数几何综合题,考查了二次函数的图象与性质、抛物线与 x 轴的交点、一元 二次方程根的解法及根与系数关系、一次函数、平行四边形的性质以及全等三角形的判定与 性质等方面的知识,涉及的考点较多,有一定的难度. 【52. 2012 福州】 22.(满分 14 分)如图①,已知抛物线 y=ax2+bx(a≠0)经过 A(3,0)、B(4,4)两点. (1) 求抛物线的解析式; (2) 将直线 OB 向下平移 m 个单位长度后,得到的直线与抛物线只有一个公共点 D, 求 m 的值及点 D 的坐标; (3) 如图②,若点 N 在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,求出所有满 足△POD∽△NOB 的点 P 的坐标(点 P、O、D 分别与点 N、O、B 对应). 考点:二次函数综合题. 分析:(1) 利用待定系数法求出二次函数解析式即可; (2) 根据已知条件可求出 OB 的解析式为 y=x,则向下平移 m 个单位长度后的解析 式为:y=x-m.由于抛物线与直线只有一个公共点,意味着联立解析式后得到的一 元二次方程,其根的判别式等于 0,由此可求出 m 的值和 D 点坐标; (3) 综合利用几何变换和相似关系求解. 方法一:翻折变换,将△NOB 沿 x 轴翻折; 方法二:旋转变换,将△NOB 绕原点顺时针旋转 90°. 特别注意求出 P 点坐标之后,该点关于直线 y=-x 的对称点也满足题意,即满足题 意的 P 点有两个,避免漏解. 解答:解:(1) ∵ 抛物线 y=ax2+bx(a≠0)经过点 A(3,0)、B(4,4). ∴ 9a+3b=0 16a+4b=4,解得: a=1 b=-3. A B D O x y 第 22 题图① A B D O x y 第 22 题图② N ∴ 抛物线的解析式是 y=x2-3x. (2) 设直线 OB 的解析式为 y=k1x,由点 B(4,4), 得:4=4k1,解得 k1=1. ∴ 直线 OB 的解析式为 y=x. ∴ 直线 OB 向下平移 m 个单位长度后的解析式为:y=x-m. ∵ 点 D 在抛物线 y=x2-3x 上. ∴ 可设 D(x,x2-3x). 又点 D 在直线 y=x-m 上, ∴ x2-3x =x-m,即 x2-4x+m=0. ∵ 抛物线与直线只有一个公共点, ∴ △=16-4m=0,解得:m=4. 此时 x1=x2=2,y=x2-3x=-2, ∴ D 点坐标为(2,-2). (3) ∵ 直线 OB 的解析式为 y=x,且 A(3,0), ∴ 点 A 关于直线 OB 的对称点 A'的坐标是(0,3). 设直线 A'B 的解析式为 y=k2x+3,过点 B(4,4), ∴ 4k2+3=4,解得:k2= 1 4 . ∴ 直线 A'B 的解析式是 y= 1 4 x+3. ∵ ∠NBO=∠ABO, ∴ 点 N 在直线 A'B 上, ∴ 设点 N(n, 1 4 n+3),又点 N 在抛物线 y=x2-3x 上, D A B O x y N A' P1 P2 ∴ 1 4 n+3=n2-3n, 解得:n1=- 3 4 ,n2=4(不合题意,会去), ∴ 点 N 的坐标为(- 3 4 , 45 16 ). 方法一:如图 1,将△NOB 沿 x 轴翻折,得到△N1OB1, 则 N1(- 3 4 ,- 45 16 ),B1(4,-4), ∴ O、D、B1 都在直线 y=-x 上. ∵△P1OD∽△NOB, ∴ △P1OD∽△N1OB1, ∴ OP1 ON1 = OD OB1 = 1 2 , ∴ 点 P1 的坐标为(- 3 8 ,- 45 32 ). 将△OP1D 沿直线 y=-x 翻折,可得另一个满足条件的点 P2( 45 32 , 3 8 ). 综上所述,点 P 的坐标是(- 3 8 ,- 45 32 )或( 45 32 , 3 8 ). 方法二:如图 2,将△NOB 绕原点顺时针旋转 90°,得到△N2OB2, 则 N2( 45 16 , 3 4 ),B2(4,-4), ∴ O、D、B2 都在直线 y=-x 上. ∵ △P1OD∽△NOB, ∴ △P1OD∽△N2OB2, 图 2 A' N2P1 P2 B2 A B D O x y N ∴ OP1 ON2 = OD OB2 = 1 2 , ∴ 点 P1 的坐标为( 45 32 , 3 8 ). 将△OP1D 沿直线 y=-x 翻折,可得另一个满足条件的点 P2(- 3 8 ,- 45 32 ). 综上所述,点 P 的坐标是(- 3 8 ,- 45 32 )或( 45 32 , 3 8 ). 点评:本题是基于二次函数的代数几何综合题,综合考查了待定系数法求抛物线解析式、一 次函数(直线)的平移、一元二次方程根的判别式、翻折变换、旋转变换以及相似三角 形等重要知识点.本题将初中阶段重点代数、几何知识熔于一炉,难度很大,对学生 能力要求极高,具有良好的区分度,是一道非常好的中考压轴题. 【53. 2012 南昌】 27.如图,已知二次函数 L1:y=x2﹣4x+3 与 x 轴交于 A.B 两点(点 A 在点 B 左边),与 y 轴交于点 C. (1)写出二次函数 L1 的开口方向、对称轴和顶点坐标; (2)研究二次函数 L2:y=kx2﹣4kx+3k(k≠0). ①写出二次函数 L2 与二次函数 L1 有关图象的两条相同的性质; ②若直线 y=8k 与抛物线 L2 交于 E、F 两点,问线段 EF 的长度是否发生变化?如果不会, 请求出 EF 的长度;如果会,请说明理由. 考点:二次函数综合题。 专题:综合题。 分析:(1)抛物线 y=ax2+bx+c 中:a 的值决定了抛物线的开口方向,a>0 时,抛物线的 开口向上;a<0 时,抛物线的开口向下. 抛物线的对称轴方程:x=﹣ ;顶点坐标:(﹣ , ). (2)①新函数是由原函数的各项系数同时乘以 k 所得,因此从二次函数的图象与解析式的 系数的关系入手进行分析. ②联系直线和抛物线 L2 的解析式,先求出点 E、F 的坐标,进而可表示出 EF 的长,若该长 度为定值,则线段 EF 的长不会发生变化. 解答:解:(1)抛物线 y=x2﹣4x+3 中,a=1、b=﹣4、c=3; ∴﹣ =﹣ =2, = =﹣1; ∴二次函数 L1 的开口向上,对称轴是直线 x=2,顶点坐标(2,﹣1). (2)①二次函数 L2 与 L1 有关图象的两条相同的性质: 对称轴为 x=2 或定点的横坐标为 2, 都经过 A(1,0),B(3,0)两点; ②线段 EF 的长度不会发生变化. ∵直线 y=8k 与抛物线 L2 交于 E、F 两点, ∴kx2﹣4kx+3k=8k, ∵k≠0,∴x2﹣4x+3=8, 解得:x1=﹣1,x2=5,∴EF=x2﹣x1=6, ∴线段 EF 的长度不会发生变化. 点评:该题主要考查的是函数的基础知识,有:二次函数的性质、函数图象交点坐标的解法 等,难度不大,但需要熟练掌握. 【54. 2012 恩施州】 24.如图,已知抛物线 y=﹣x2+bx+c 与一直线相交于 A(﹣1,0),C(2,3)两点,与 y 轴交于点 N.其顶点为 D. (1)抛物线及直线 AC 的函数关系式; (2)设点 M(3,m),求使 MN+MD 的值最小时 m 的值; (3)若抛物线的对称轴与直线 AC 相交于点 B,E 为直线 AC 上的任意一点,过点 E 作 EF∥BD 交抛物线于点 F,以 B,D,E,F 为顶点的四边形能否为平行四边形?若能,求点 E 的坐标; 若不能,请说明理由; (4)若 P 是抛物线上位于直线 AC 上方的一个动点,求△APC 的面积的最大值. 考点: 二次函数综合题。 分析: (1)利用待定系数法求二次函数解析式、一次函数解析式; (2)根据两点之间线段最短作 N 点关于直线 x=3 的对称点 N′,当 M(3,m)在 直线 DN′上时,MN+MD 的值最小; (3)需要分类讨论:①当点 E 在线段 AC 上时,点 F 在点 E 上方,则 F(x,x+3) 和②当点 E 在线段 AC(或 CA)延长线上时,点 F 在点 E 下方,则 F(x,x﹣1), 然后利用二次函数图象上点的坐标特征可以求得点 E 的坐标; (4)方法一:过点 P 作 PQ⊥x 轴交 AC 于点 Q;过点 C 作 CG⊥x 轴于点 G,如图 1.设 Q(x,x+1),则 P(x,﹣x2+2x+3).根据两点间的距离公式可以求得线段 PQ=﹣x2+x+2;最后由图示以及三角形的面积公式知 S△APC=﹣ (x﹣ )2+ , 所以由二次函数的最值的求法可知△APC 的面积的最大值; 方法二:过点 P 作 PQ⊥x 轴交 AC 于点 Q,交 x 轴于点 H;过点 C 作 CG⊥x 轴于 点 G,如图 2.设 Q(x,x+1),则 P(x,﹣x2+2x+3).根据图示以及三角形的面 积公式知 S△APC=S△APH+S 直角梯形 PHGC﹣S△AGC=﹣ (x﹣ )2+ ,所以由二次函数 的最值的求法可知△APC 的面积的最大值; 解答: 解:(1)由抛物线 y=﹣x2+bx+c 过点 A(﹣1,0)及 C(2,3)得, , 解得 , 故抛物线为 y=﹣x2+2x+3 又设直线为 y=kx+n 过点 A(﹣1,0)及 C(2,3)得 , 解得 故直线 AC 为 y=x+1; (2)作 N 点关于直线 x=3 的对称点 N′,则 N′(6, 3),由(1)得 D(1,4), 故直线 DN′的函数关系式为 y=﹣ x+ , 当 M(3,m)在直线 DN′上时,MN+MD 的值最小, 则 m=﹣ × = ; (3)由(1)、(2)得 D(1,4),B(1,2) ∵点 E 在直线 AC 上, 设 E(x,x+1), ①当点 E 在线段 AC 上时,点 F 在点 E 上方, 则 F(x,x+3), ∵F 在抛物线上, ∴x+3=﹣x2+2x+3, 解得,x=0 或 x=1(舍去) ∴E(0,1); ②当点 E 在线段 AC(或 CA)延长线上时,点 F 在点 E 下方, 则 F(x,x﹣1) 由 F 在抛物线上 ∴x﹣1=﹣x2+2x+3 解得 x= 或 x= ∴E( , )或( , ) 综上,满足条件的点 E 为 E(0,1)、( , )或( , ); (4)方法一:过点 P 作 PQ⊥x 轴交 AC 于点 Q;过点 C 作 CG⊥x 轴于点 G,如图 1 设 Q(x,x+1),则 P(x,﹣x2+2x+3) ∴PQ=(﹣x2+2x+3)﹣(x﹣1) =﹣x2+x+2 又∵S△APC=S△APQ+S△CPQ= PQ•AG = (﹣x2+x+2)×3 =﹣ (x﹣ )2+ ∴面积的最大值为 . 方法二:过点 P 作 PQ⊥x 轴交 AC 于点 Q,交 x 轴于点 H;过点 C 作 CG⊥x 轴于 点 G,如图 2, 设 Q(x,x+1),则 P(x,﹣x2+2x+3) 又∵S△APC=S△APH+S 直角梯形 PHGC﹣S△AGC= (x+1)(﹣x2+2x+3)+ (﹣x2+2x+3+3) (2﹣x)﹣ ×3×3 =﹣ x2+ x+3 =﹣ (x﹣ )2+ ∴△APC 的面积的最大值为 . 点评: 本题考查了二次函数综合题.解答(3)题时,要对点 E 所在的位置进行分类讨论, 以防漏解. 【55. 2012 兰州】 28.如图,Rt△ABO 的两直角边 OA、OB 分别在 x 轴的负半轴和 y 轴的正半轴上,O 为坐 标原点,A、B 两点的坐标分别为(-3,0)、(0,4),抛物线 y= x2+bx+c 经过点 B,且 顶点在直线 x= 上. (1)求抛物线对应的函数关系式; (2)若把△ABO 沿 x 轴向右平移得到△DCE,点 A、B、O 的对应点分别是 D、C、E,当四边 形 ABCD 是菱形时,试判断点 C 和点 D 是否在该抛物线上,并说明理由; (3)在(2)的条件下,连接 BD,已知对称轴上存在一点 P 使得△PBD 的周长最小,求出 P 点 的坐标; (4)在(2)、(3)的条件下,若点 M 是线段 OB 上的一个动点(点 M 与点 O、B 不重合),过点 M 作∥BD 交 x 轴于点 N,连接 PM、PN,设 OM 的长为 t,△PMN 的面积为 S,求 S 和 t 的函数关系式,并写出自变量 t 的取值范围,S 是否存在最大值?若存在,求出最大值和此 时 M 点的坐标;若不存在,说明理由. 考点: 二次函数综合题。 分析: (1)根据抛物线 y= 经过点 B(0,4),以及顶点在直线 x= 上,得出 b,c 即可; (2)根据菱形的性质得出 C、D 两点的坐标分别是(5,4)、(2,0),利用图象上点的 性质得出 x=5 或 2 时,y 的值即可. (3)首先设直线 CD 对应的函数关系式为 y=kx+b,求出解析式,当 x= 时,求出 y 即可; (4)利用 MN∥BD,得出△OMN∽△OBD,进而得出 ,得到 ON= ,进而表 示出△PMN 的面积,利用二次函数最值求出即可. 解答: 解:(1)∵抛物线 y= 经过点 B(0,4) ∴c=4, ∵顶点在直线 x= 上, ∴ ; ∴所求函数关系式为 ; (2)在 Rt△ABO 中,OA=3,OB=4, ∴AB= , ∵四边形 ABCD 是菱形, ∴BC=CD=DA=AB=5, ∴C、D 两点的坐标分别是(5,4)、(2,0), 当 x=5 时,y= , 当 x=2 时,y= , ∴点 C 和点 D 都在所求抛物线上; (3)设 CD 与对称轴交于点 P,则 P 为所求的点, 设直线 CD 对应的函数关系式为 y=kx+b, 则 , 解得: , ∴ , 当 x= 时,y= , ∴P( ), (4)∵MN∥BD, ∴△OMN∽△OBD, ∴ 即 得 ON= 设对称轴交 x 于点 F, 则 (PF + OM)•OF = ( + t)× , ∵ , ( )× = , S= (- ), =- (0<t<4), S 存在最大值. 由 S=- (t- )2+ , ∴当 S= 时,S 取最大值是 , 此时,点 M 的坐标为(0, ). 点评: 此题主要考查了二次函数的综合应用,以及菱形性质和待定系数法求解析式,求图 形面积最值,利用二次函数的最值求出是解题关键. 【56. 2012 南通】 28.(本小题满分 14 分) 如图,经过点 A(0,-4)的抛物线 y= 1 2 x2+bx+c 与 x 轴相交于点 B(-0,0)和 C,O 为坐标原点. (1)求抛物线的解析式; (2)将抛物线 y= 1 2 x2+bx+c 向上平移 7 2 个单位长 度、再向左平移 m(m>0)个单位长度,得到新抛物线.若新抛物线的顶点 P 在△ABC 内,求 m 的取值范围; (3)设点 M 在 y 轴上,∠OMB+∠OAB=∠ACB,求 AM 的长. 【考点】二次函数综合题. 【专题】分类讨论. 【分析】(1)该抛物线的解析式中只有两个待定系数,只需将 A、B 两点坐标代入即可得 解. (2)首先根据平移条件表示出移动后的函数解析式,进而用 m 表示出该函数的顶 点坐标,将其代入直线 AB、AC 的解析式中,即可确定 P 在△ABC 内时 m 的取 值范围. (3)先在 OA 上取点 N,使得∠ONB=∠ACB,那么只需令∠NBA=∠OMB 即可,显 然在 y 轴的正负半轴上都有一个符合条件的 M 点;以 y 轴正半轴上的点 M 为 例,先证△ABN、△AMB 相似,然后通过相关比例线段求出 AM 的长. 【解答】解:(1)将 A(0,-4)、B(-2,0)代入抛物线 y= 1 2 x2+bx+c 中,得: 0+c=-4 1 2 ×4-2b+c=0 , 解得: b=-1 c=-4 ∴抛物线的解析式:y= 1 2 x2-x-4. (2)由题意,新抛物线的解析式可表示为: y= 1 2 (x+m)2-(x+m)-4+7 2 , 即:y= 1 2 x2+(m-1)x+1 2 m2-m-1 2 ; 它的顶点坐标 P:(1-m,-1); 由(1)的抛物线解析式可得:C(4,0); 那么直线 AB:y=-2x-4;直线 AC:y=x-4; 当点 P 在直线 AB 上时,-2(1-m)-4=-1,解得:m=5 2 ; 当点 P 在直线 AC 上时,(1-m)-4=-1,解得:m=-2; ∴当点 P 在△ABC 内时,-2<m<5 2 ; 又∵m>0, ∴符合条件的 m 的取值范围:0<m<5 2 . (3)由 A(0,-4)、B(4,0)得:OA=OC=4,且△OAC 是等腰直角三角形; 如图,在 OA 上取 ON=OB=2,则∠ONB=∠ACB=45°; ∴∠ONB=∠NBA+OAB=∠ACB=∠OMB+∠OAB,即∠ONB=∠OMB; 如图,在△ABN、△AM1B 中, ∠BAN=∠M1AB,∠ABN=∠AM1B, ∴△ABN∽△AM1B,得:AB2=AN•AM1; 易得:AB2=(-2)2+42=20,AN=OA-ON=4-2=2; ∴AM1=20÷2=10,OM1=AM1-OA=10-4=6; 而∠BM1A=∠BM2A=∠ABN, ∴OM1=OM2=6,AM2=OM2-OA=6-4=2. 综上,AM 的长为 6 或 2. 【点评】考查了二次函数综合题,该函数综合题的难度较大,(3)题注意分类讨论,通过 构建相似三角形是打开思路的关键所在. 【57. 2012 荆门】 24. 如图甲,四边形 OABC 的边 OA、OC 分别在 x 轴、y 轴的正半轴上,顶点在 B 点的抛 物线交 x 轴于点 A、D,交 y 轴于点 E,连接 AB、AE、BE.已知 tan∠CBE= ,A(3,0), D(﹣1,0),E(0,3). (1)求抛物线的解析式及顶点 B 的坐标; (2)求证:CB 是△ABE 外接圆的切线 (3)试探究坐标轴上是否存在一点 P,使以 D、E、P 为顶点的三角形与△ABE 相似,若存 在,直接写出点 P 的坐标;若不存在,请说明理由; (4)设△AOE 沿 x 轴正方向平移 t 个单位长度(0<t≤3)时,△AOE 与△ABE 重叠部分的 面积为 s,求 s 与 t 之间的函数关系式,并指出 t 的取值范围. 解:由题意,设抛物线解析式为 y=a(x﹣3)(x+1). 将 E(0,3)代入上式,解得:a=﹣1. ∴y=﹣x2+2x+3. 则点 B(1,4). (2)证明:如图 1,过点 B 作 BM⊥y 于点 M,则 M(0,4). 在 Rt△AOE 中,OA=OE=3, ∴∠1=∠2=45°,AE= =3 . 在 Rt△EMB 中,EM=OM﹣OE=1=BM, ∴∠MEB=∠MBE=45°,BE= = . ∴∠BEA=180°﹣∠1﹣∠MEB=90°. ∴AB 是△ABE 外接圆的直径. 在 Rt△ABE 中,tan∠BAE= = =tan∠CBE, ∴∠BAE=∠CBE. 在 Rt△ABE 中,∠BAE+∠3=90°,∴∠CBE+∠3=90°. ∴∠CBA=90°,即 CB⊥AB. ∴CB 是△ABE 外接圆的切线. (3)解:Rt△ABE 中,∠AEB=90°,tan∠BAE= ,sin∠BAE= ,cos∠BAE= ; 若以 D、E、P 为顶点的三角形与△ABE 相似,则△DEP 必为直角三角形; ①DE 为斜边时,P1 在 x 轴上,此时 P1 与 O 重合; 由 D(﹣1,0)、E(0,3),得 OD=1、OE=3,即 tan∠DEO= =tan∠BAE,即∠DEO= ∠BAE 满足△DEO∽△BAE 的条件,因此 O 点是符合条件的 P1 点,坐标为(0,0). ②DE 为短直角边时,P2 在 x 轴上; 若以 D、E、P 为顶点的三角形与△ABE 相似,则∠DEP2=∠AEB=90°,sin∠DP2E=sin∠ BAE= ; 而 DE= = ,则 DP2=DE÷sin∠DP2E= ÷ =10,OP2=DP2﹣OD=9 即:P2(9,0); ③DE 为长直角边时,点 P3 在 y 轴上; 若以 D、E、P 为顶点的三角形与△ABE 相似,则∠EDP3=∠AEB=90°,cos∠DEP3=cos∠ BAE= ; 则 EP3=DE÷cos∠DEP3= ÷ = ,OP3=EP3﹣OE= ; 综上,得:P1(0,0),P2(9,0),P3(0,﹣ ). (4)解:设直线 AB 的解析式为 y=kx+b. 将 A(3,0),B(1,4)代入,得 解得 ∴y=﹣2x+6. 过点 E 作射线 EF∥x 轴交 AB 于点 F,当 y=3 时,得 x= ,∴F( ,3). 情况一:如图 2,当 0<t≤ 时,设△AOE 平移到△DNM 的位置,MD 交 AB 于点 H,MN 交 AE 于点 G. 则 ON=AD=t,过点 H 作 LK⊥x 轴于点 K,交 EF 于点 L. 由△AHD∽△FHM,得 ,即 . 解得 HK=2t. ∴S 阴=S△MND﹣S△GNA﹣S△HAD= ×3×3﹣ (3﹣t)2﹣ t•2t=﹣ t2+3t. 情况二:如图 3,当 <t≤3 时,设△AOE 平移到△PQR 的位置,PQ 交 AB 于点 I,交 AE 于点 V. 由△IQA∽△IPF,得 .即 , 解得 IQ=2(3﹣t). ∴S 阴=S△IQA﹣S△VQA= ×(3﹣t)×2(3﹣t)﹣ (3﹣t)2= (3﹣t)2= t2﹣3t+ . 综上所述:s= . 【58. 2012 常德】 25、如图 11,已知二次函数 ))(2(48 1 baxxy 的图像过点 A(-4,3),B(4,4). (1)求二次函数的解析式: (2)求证:△ACB 是直角三角形; (3)若点 P 在第二象限,且是抛物线上的一动点,过点 P 作 PH 垂直 x 轴于点 H,是否 存在以 P、H、D、为顶点的三角形与△ABC 相似?若存在,求出点 P 的坐标;若不存在, 请 说明理由。 知识点考察:①二次函数解析式的确定, ②勾股定理及其逆定理的应用, ③相似三角形的性质, ④坐标系中点的坐标的特征, ⑤抛物线与 X 轴的交点,⑥一元二次方程的解法, ⑦垂直的定义。 ⑧二元一次方程组的解法。 能力考察:①观察能力,②逻辑思维与推理能力,③书写表达能力, ④综合运用知识的能力,⑤分类讨论的能力。⑥动点的探求能力 ⑦准确的计算能力。 分析:①求二次函数的解析式,也就是要求 ))(2(48 1 baxxy 中 a、b 的值, 只要把 A(-4,3),B(4,4)代人即可。 ②求证△ACB 是直角三角形,只要求出 AC,BC,AB 的长度,然后用 勾股定理及其逆定理去考察。 ③是否存在以 P、H、D、为顶点的三角形与△ABC 相似?先要选择一点 P 然后自 P 点作垂线构成 Rt△PHD,把两个三角形相似作条件,运用三角形 相似的性质去构建关于 P 点横坐标的方程。 解:(1)将 A(-4,3),B(4,4)代人 ))(2(48 1 baxxy 中,整理得: 324 72-4 ba ba 解得 20- 13 b a ∴二次函数的解析式为: )20-13)(2(48 1 xxy , 整理得: ( 2 ) 由 整理 040-613 2 xx ∴X1=-2 ,X2= 13 20 ∴C (-2,0) D ),( 013 20 从而有:AC2=4+9 BC2=36+16 AC2+ BC2=13+52=65 AB2=64+1=65 ∴ AC2+ BC2=AB2 故△ACB 是直角三角形 (3)设 )6 5-8 1 48 13( 2 xxxp , (X<0) PH= 6 5-8 1 48 13 2 xx HD= x-13 20 AC= 13 BC= 132 06 5-8 1 48 13 2 xx 6 5-8 1 48 13 2 xxy ①当△PHD∽△ACB 时有: BC HD AC PH 即: 132 -13 20 13 6 5-8 1 48 13 2 xxx 整理 039 125-4 5 24 13 2 xx ∴ 13 50-1 x 13 20 2 x (舍去)此时, 13 35 1 y ∴ ), 13 35 13 50(-1p ②当△DHP∽△ACB 时有: BC PH AC DH 即: 132 6 5-8 1 48 13 13 -13 20 2 xxx 整理 078 305-8 17 48 13 2 xx ∴ 13 122-1 x 13 20 2 x (舍去)此时, 13 284 1 y ∴ ), 13 284 13 122(-2p 综上所述,满足条件的点有两个即 ), 13 35 13 50(-1p ), 13 284 13 122(-2p 点评:这是一个二次函数开放性的综合题,解决问题的思路容易建立,切入点也好找, 但运算难度较大。出题的老师看准了我们的学生在学习中存在的问题,那就是 每一个学生在计算时无论简单与复杂总是离不开计算器,所以遇到分数运算时 没有信心进行运算,最后还是放弃了。因此在这里要提醒每一位学生在平时计 算的练习中多用心算和笔算,才能提高自己的运算能力。 【59. 2012•黔东南州】 24.如图,已知抛物线经过点 A(﹣1,0)、B(3,0)、C(0,3)三点. (1)求抛物线的解析式. (2)点 M 是线段 BC 上的点(不与 B,C 重合),过 M 作 MN∥y 轴交抛物线于 N,若点 M 的横坐标为 m,请用 m 的代数式表示 MN 的长. (3)在(2)的条件下,连接 NB、NC,是否存在 m,使△BNC 的面积最大?若存在,求 m 的值;若不存在,说明理由. 解析:(1)设抛物线的解析式为:y=a(x+1)(x﹣3),则: a(0+1)(0﹣3)=3,a=﹣1; ∴抛物线的解析式:y=﹣(x+1)(x﹣3)=﹣x2+2x+3. (2)设直线 BC 的解析式为:y=kx+b,则有: , 解得 ; 故直线 BC 的解析式:y=﹣x+3. 已知点 M 的横坐标为 m,则 M(m,﹣m+3)、N(m,﹣m2+2m+3); ∴故 N=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m(0<m<3). (3)如图; ∵S△BNC=S△MNC+S△MNB= MN(OD+DB)= MN•OB, ∴S△BNC= (﹣m2+3m)•3=﹣ (m﹣ )2+ (0<m<3); ∴当 m= 时,△BNC 的面积最大,最大值为 . 【60. 2012 广东珠海】 21. 如图,在等腰梯形 ABCD 中,ABDC,AB= ,DC= ,高 CE= ,对角线 AC、 BD 交于 H,平行于线段 BD 的两条直线 MN、RQ 同时从点 A 出发沿 AC 方向向点 C 匀速 平移,分别交等腰梯形 ABCD 的边于 M、N 和 R、Q,分别交对角线 AC 于 F、G;当直线 RQ 到达点 C 时,两直线同时停止移动.记等腰梯形 ABCD 被直线 MN 扫过的图形面积为 S1、被直线 RQ 扫过的图形面积为 S2,若直线 MN 平移的速度为 1 单位/秒,直线 RQ 平移 的速度为 2 单位/秒,设两直线移动的时间为 x 秒. (1)填空:∠AHB= ;AC= ; (2)若 S2=3S1,求 x; (3)设 S2=mS1,求 m 的变化范围. 解:(1)过点 C 作 CK∥BD 交 AB 的延长线于 K, ∵CD∥AB, ∴四边形 DBKC 是平行四边形, ∴BK=CD= ,CK=BD, ∴AK=AB+BK=3 + =4 , ∵四边形 ABCD 是等腰梯形, ∴BD=AC, ∴AC=CK, ∴BK=EK= AK=2 =CE, ∵CE 是高, ∴∠K=∠KCE=∠ACE=∠CAE=45°, ∴∠ACK=90°, ∴∠AHB=∠ACK=90°, ∴AC=AK•cos45°=4 × =4; 故答案为:90°,4; (2)直线移动有两种情况:0<x< 及 ≤x≤2. ①当 0<x< 时, ∵MN∥BD, ∴△AMN∽△ARQ,△ANF∽△QG, ∴ =4, ∴S2=4S1≠3S1; ②当 ≤x≤2 时, ∵AB∥CD, ∴△ABH∽△CDH, ∴CH:AH=CD:AB=DH:BH=1:3, ∴CH=DH= AC=1,AH═BH=4﹣1=3, ∵CG=4﹣2x,AC⊥BD, ∴S△BCD= ×4×1=2, ∵RQ∥BD, ∴△CRQ∽△CDB, ∴S△CRQ=2×( )2=8(2﹣x)2, ∵S 梯形 ABCD= (AB+CD)•CE= ×(3 + )×2 =8,S△ ABD= AB•CE= ×3 ×2 =6, ∵MN∥BD, ∴△AMN∽△ADB, ∴ , ∴S1= x2,S2=8﹣8(2﹣x)2, ∵S2=3S1, ∴8﹣8(2﹣x)2=3× x2, 解得:x1= < (舍去),x2=2 ∴x 的值为 2; (3)由(2)得: 当 0<x< 时,m=4, 当 ≤x≤2 时, ∵S2=mS1, ∴m= = =﹣ + ﹣12=﹣36( ﹣ )2+4, ∴m 是 的二次函数,当 ≤x≤2 时,即当 ≤ ≤ 时,m 随 的增大而增大, ∴当 x= 时,m 最大,最大值为 4, 当 x=2 时,m 最小,最小值为 3, ∴m 的变化范围为:3≤m≤4. (61. 2012 广东深圳 9 分)23.如图,在平面直角坐标系中,直线l :y=-2x+b (b≥0)的 位置随 b 的不同取值而变化. (1)已知⊙M 的圆心坐标为(4,2),半径为 2. 当 b= 时,直线l :y=-2x+b (b≥0)经过圆心 M: 当 b= 时,直线l :y=-2x+b(b≥0)与 OM 相切: (2)若把⊙M 换成矩形 ABCD,其三个顶点坐标分别为:A(2,0)、B(6,0)、C(6, 2). 设直线 l 扫过矩形 ABCD 的面积为 S,当 b 由小到大变化时,请求出 S 与 b 的函数关 系式, 【答案】解:(1)10;10 2 5 。 (2)由 A(2,0)、B(6,0)、C(6,2),根据矩形的性质,得 D (2,2)。 如图,当直线 l 经过 A(2,0)时,b=4;当直线 l 经过 D(2,2) 时,b=6;当直线l 经过 B(6,0)时,b=12;当直线l 经过 C(6,2)时,b=14。 当 0≤b≤4 时,直线 l 扫过矩形 ABCD 的面积 S 为 0。 当 4<b≤6 时,直线 l 扫过矩形 ABCD 的面积 S 为△EFA 的面积(如图 1), 在 y=-2x+b 中,令 x=2,得 y=-4+b,则 E(2,-4 +b), 令 y=0,即-2x+b=0,解得 x= 1 b2 ,则 F( 1 b2 ,0)。 ∴AF= 1 b 22 ,AE=-4+b。 ∴S= 21 1 1 1AF AE b 2 4 b b 2b+42 2 2 4 - + - 。 当 6<b≤12 时,直线 l 扫过矩形 ABCD 的面积 S 为直角梯 形 DHGA 的面积(如图 2), 在 y=-2x+b 中,令 y=0,得 x= 1 b2 ,则 G( 1 b2 ,0), 令 y=2,即-2x+b=2,解得 x= 1 b 12 ,则 H( 1 b 12 ,2)。 ∴DH= 1 b 32 ,AG= 1 b 22 。AD=2 ∴S= 1 1DH+AG AD b 5 2 b 52 2 。 当 12<b≤14 时,直线l 扫过矩形 ABCD 的面积 S 为五 边形 DMNBA 的面积=矩形 ABCD 的面积-△CMN 的面积(如图 2) 在 y=-2x+b 中,令 y=2,即-2x+b=2,解得 x= 1 b 12 ,则 M( 1 b 12 ,0), 令 x=6,得 y=-12+b,,则 N(6,-12+b)。 ∴MC= 17 b2 ,NC=14-b。 ∴S= 21 1 1 14 2 MC NC 8 7 b 14 b b +7b 412 2 2 4 - 。 当 b>14 时,直线 l 扫过矩形 ABCD 的面积 S 为矩形 ABCD 的面积,面 积为民 8。 综上所述。S 与 b 的函数关系式为: 2 2 0 0 b 4 1 b 2b+4 4 b 64 S b 5 6 b 1 1 b +7b 41 12 b 144 8 b 14 < < < > - 。 【考点】直线平移的性质,相似三角形的判定和性质,待定系数法,曲线上点的坐标与方程 的关系,直线与圆相切的性质,勾股定理,解一元二次方程,矩形的性质。 【分析】(1)①∵直线 y=-2x+b (b≥0)经过圆心 M(4,2), ∴2=-2×4+b,解得 b=10。 ②如图,作点 M 垂直于直线 y=-2x+b 于点 P,过 点 P 作 PH∥x 轴,过点 M 作 MH⊥PH,二者交于点 H。设直线 y=- 2x+b 与 x,y 轴分别交于点 A,B。 则由△OAB∽△HMP,得 MH AO 1 PH OB 2 。 ∴可设直线 MP 的解析式为 1 1y x b2 + 。 由 M(4,2),得 1 12 4 b2 + ,解得 1b 0 。∴直线 MP 的解析式为 1y x2 。 联立 y=-2x+b 和 1y x2 ,解得 2 1x= b, y b5 5 。 ∴P( 2 1b, b5 5 )。 由 PM=2,勾股定理得, 2 22 1b + b 45 5 -4 -2 ,化简得 24b 20b+80=0- 。 解得 b=10 2 5 。 (2)求出直线l 经过点 A、B、C、D 四点时 b 的值,从而分 0≤b≤4,4<b≤6,6< b≤12,12<b≤14,b>14 五种情况分别讨论即可。 (62.2012 重庆)24.已知:如图,在菱形 ABCD 中,F 为边 BC 的中点,DF 与对角线 AC 交于点 M,过 M 作 ME⊥CD 于点 E,∠1=∠2. (1)若 CE=1,求 BC 的长; (2)求证:AM=DF+ME. 考点:菱形的性质;全等三角形的判定与性质。 解答:(1)解:∵四边形 ABCD 是菱形, ∴AB∥CD, ∴∠1=∠ACD, ∵∠1=∠2, ∴∠ACD=∠2, ∴MC=MD, ∵ME⊥CD, ∴CD=2CE, ∵CE=1, ∴CD=2, ∴BC=CD=2; (2)证明:如图,∵F 为边 BC 的中点, ∴BF=CF= BC, ∴CF=CE, 在菱形 ABCD 中,AC 平分∠BCD, ∴∠ACB=∠ACD, 在△CEM 和△CFM 中, ∵ , ∴△CEM≌△CFM(SAS), ∴ME=MF, 延长 AB 交 DF 于点 G, ∵AB∥CD, ∴∠G=∠2, ∵∠1=∠2, ∴∠1=∠G, ∴AM=MG, 在△CDF 和△BGF 中, ∵ , ∴△CDF≌△BGF(AAS), ∴GF=DF, 由图形可知,GM=GF+MF, ∴AM=DF+ME. (63.2012 重庆)25.企业的污水处理有两种方式,一种是输送到污水厂进行集中处理, 另一种是通过企业的自身设备进行处理.某企业去年每月的污水量均为 12000 吨,由于污 水厂处于调试阶段,污水处理能力有限,该企业投资自建设备处理污水,两种处理方式同时 进行.1 至 6 月,该企业向污水厂输送的污水量 y1(吨)与月份 x(1≤x≤6,且 x 取整数) 之间满足的函数关系如下表: 7 至 12 月,该企业自身处理的污水量 y2(吨)与月份 x(7≤x≤12,且 x 取整数)之间满 足二次函数关系式为 )0(2 2 acaxy .其图象如图所示.1 至 6 月,污水厂处理每吨 污水的费用: 1z (元)与月份 x 之间满足函数关系式: xz 2 1 1 ,该企业自身处理每吨污 水的费用: 2z (元)与月份 x 之间满足函数关系式: 2 2 12 1 4 3 xxz ;7 至 12 月,污水 厂处理每吨污水的费用均为 2 元,该企业自身处理每吨污水的费用均为 1.5 元. (1)请观察题中的表格和图象,用所学过的一次函数、反比例函数或二次函数的有关知识, 分别直接写出 21,yy 与 x 之间的函数关系式; (2)请你求出该企业去年哪个月用于污水处理的费用 W(元)最多,并求出这个最多费用; (3)今年以来,由于自建污水处理设备的全面运行,该企业决定扩大产能并将所有污水全 部自身处理,估计扩大产能后今年每月的污水量都将在去年每月的基础上增加 a%,同时每 吨污水处理的费用将在去年 12 月份的基础上增加(a﹣30)%,为鼓励节能降耗,减轻企 业负担,财政对企业处理污水的费用进行 50%的补助.若该企业每月的污水处理费用为 18000 元,请计算出 a 的整数值. (参考数据: ≈15.2, ≈20.5, ≈28.4) 考点:二次函数的应用。 解答:解:(1)根据表格中数据可以得出 xy=定值,则 y1 与 x 之间的函数关系为反比例函 数关系: y1= ,将(1,12000)代入得: k=1×12000=12000, 故 y1= (1≤x≤6,且 x 取整数); 根据图象可以得出:图象过(7, 10049),(12,10144)点, 代入 得: , 解得: , 故 y2=x2+10000(7≤x≤12,且 x 取整数); (2)当 1≤x≤6,且 x 取整数时: W=y1x1+(12000﹣y1)•x2= • x+(12000﹣ )•( x﹣ x2), =﹣1000x2+10000x﹣3000, ∵a=﹣1000<0,x=﹣ =5,1≤x≤6, ∴当 x=5 时,W 最大=22000(元), 当 7≤x≤12 时,且 x 取整数时, W=2×(12000﹣y1)+1.5y2=2×(12000﹣x2﹣10000)+1.5(x2+10000), =﹣ x2+1900, ∵a=﹣ <0,x=﹣ =0, 当 7≤x≤12 时,W 随 x 的增大而减小, ∴当 x=7 时,W 最大=18975.5(元), ∵22000>18975.5, ∴去年 5 月用于污水处理的费用最多,最多费用是 22000 元; (3)由题意得:12000(1+a%)×1.5×[1+(a﹣30)%]×(1﹣50%)=18000, 设 t=a%,整理得:10t2+17t﹣13=0, 解得:t= , ∵ ≈28.4, ∴t1≈0.57,t2≈﹣2.27(舍去), ∴a≈57, 答:a 的值是 57. 26.(2012 重庆)已知:如图,在直角梯形 ABCD 中,AD∥BC,∠B=90°,AD=2,BC=6, AB=3.E 为 BC 边上一点,以 BE 为边作正方形 BEFG,使正方形 BEFG 和梯形 ABCD 在 BC 的同侧. (1)当正方形的顶点 F 恰好落在对角线 AC 上时,求 BE 的长; (2)将(1)问中的正方形 BEFG 沿 BC 向右平移,记平移中的正方形 BEFC 为正方形 B′EFG, 当点 E 与点 C 重合时停止平移.设平移的距离为 t,正方形 B′EFG 的边 EF 与 AC 交于点 M, 连接 B′D,B′M,DM,是否存在这样的 t,使△B′DM 是直角三角形?若存在,求出 t 的值; 若不存在,请说明理由; (3)在(2)问的平移过程中,设正方形 B′EFG 与△ADC 重叠部分的面积为 S,请直接写 出 S 与 t 之间的函数关系式以及自变量 t 的取值范围. 考点:相似三角形的判定与性质;勾股定理;正方形的性质;直角梯形。 解答:解:(1)如图①, 设正方形 BEFG 的边长为 x, 则 BE=FG=BG=x, ∵AB=3,BC=6, ∴AG=AB﹣BG=3﹣x, ∵GF∥BE, ∴△AGF∽△ABC, ∴ , 即 , 解得:x=2, 即 BE=2; (2)存在满足条件的 t, 理由:如图②,过点 D 作 DH⊥BC 于 H, 则 BH=AD=2,DH=AB=3, 由题意得:BB′=HE=t,HB′=|t﹣2|,EC=4﹣t, 在 Rt△B′ME 中,B′M2=ME2+B′E2=22+(2﹣ t)2= t2﹣2t+8, ∵EF∥AB, ∴△MEC∽△ABC, ∴ ,即 , ∴ME=2﹣ t, 在 Rt△DHB′中,B′D2=DH2+B′H2=32+(t﹣2)2=t2﹣4t+13, 过点 M 作 MN⊥DH 于 N, 则 MN=HE=t,NH=ME=2﹣ t, ∴DN=DH﹣NH=3﹣(2﹣ t)= t+1, 在 Rt△DMN 中,DM2=DN2+MN2= t2+t+1, (Ⅰ)若∠DB′M=90°,则 DM2=B′M2+B′D2, 即 t2+t+1=( t2﹣2t+8)+(t2﹣4t+13), 解得:t= , (Ⅱ)若∠B′MD=90°,则 B′D2=B′M2+DM2, 即 t2﹣4t+13=( t2﹣2t+8)+( t2+t+1), 解得:t1=﹣3+ ,t2=﹣3﹣ (舍去), ∴t=﹣3+ ; (Ⅲ)若∠B′DM=90°,则 B′M2=B′D2+DM2, 即: t2﹣2t+8=(t2﹣4t+13)+( t2+t+1), 此方程无解, 综上所述,当 t= 或﹣3+ 时,△B′DM 是直角三角形; (3)①如图③,当 F 在 CD 上时,EF:DH=CE:CH, 即 2:3=CE:4, ∴CE= , ∴t=BB′=BC﹣B′E﹣EC=6﹣2﹣ = , ∵ME=2﹣ t, ∴FM= t, 当 0≤t≤ 时,S=S△FMN= ×t× t= t2, ②当 G 在 AC 上时,t=2, ∵EK=EC•tan∠DCB=EC• = (4﹣t)=3﹣ t, ∴FK=2﹣EK= t﹣1, ∵NL= AD= , ∴FL=t﹣ , ∴当 <t≤2 时,S=S△FMN﹣S△FKL= t2﹣ (t﹣ )( t﹣1)=﹣ t2+t﹣ ; ③如图⑤,当 G 在 CD 上时,B′C:CH=B′G:DH, 即 B′C:4=2:3, 解得:B′C= , ∴EC=4﹣t=B′C﹣2= , ∴t= , ∵B′N= B′C= (6﹣t)=3﹣ t, ∵GN=GB′﹣B′N= t﹣1, ∴当 2<t≤ 时,S=S 梯形 GNMF﹣S△FKL= ×2×( t﹣1+ t)﹣ (t﹣ )( t﹣1)=﹣ t2+2t ﹣ , ④如图⑥,当 <t≤4 时, ∵B′L= B′C= (6﹣t),EK= EC= (4﹣t),B′N= B′C= (6﹣t)EM= EC= (4﹣t), S=S 梯形 MNLK=S 梯形 B′EKL﹣S 梯形 B′EMN=﹣ t+ . 综上所述: 当 0≤t≤ 时,S= t2, 当 <t≤2 时,S=﹣ t2+t﹣ ; 当 2<t≤ 时,S=﹣ t2+2t﹣ , 当 <t≤4 时,S=﹣ t+ .查看更多