- 2021-05-10 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2021高考数学一轮复习第8章立体几何初步第6节立体几何中的综合问题教学案文北师大版
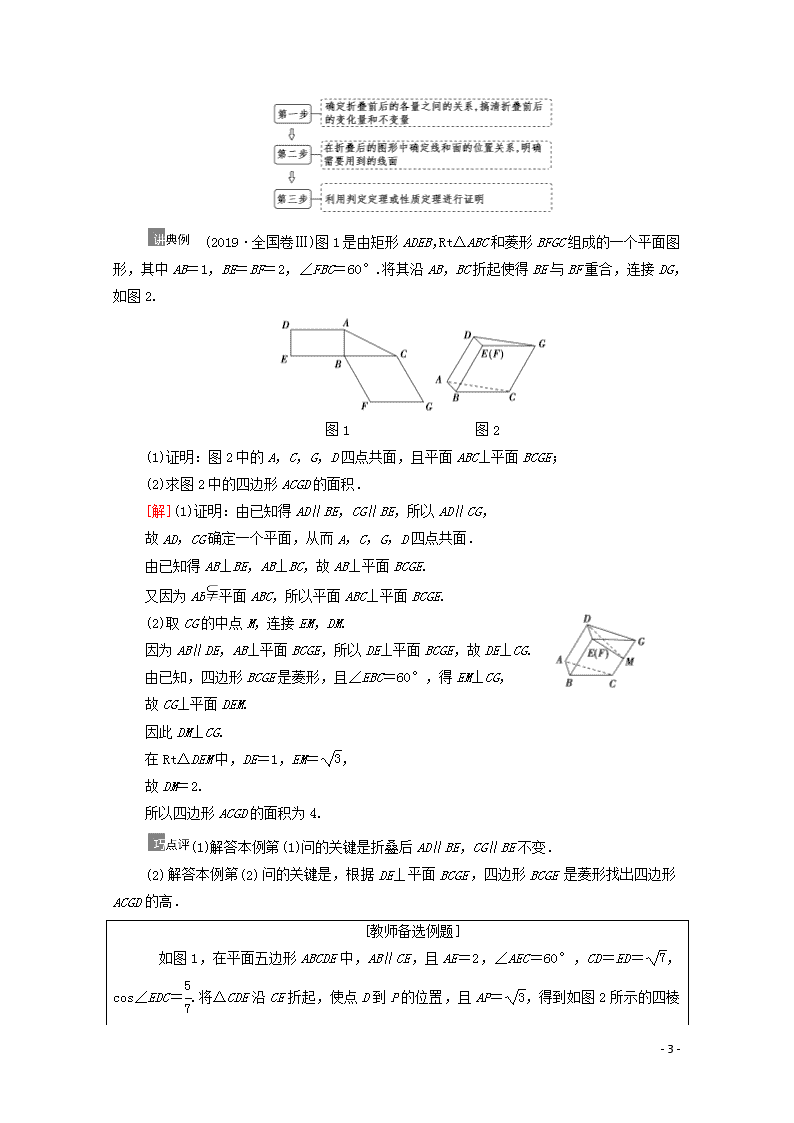
第六节 立体几何中的综合问题 (对应学生用书第140页) ⊙考点1 线面位置关系与体积计算 转化思想的应用 (1)证明线面平行、面面平行可转化为证明线线平行;证明线线平行可以转化为证明线面平行或面面平行. (2)从解题方法上讲,由于线线垂直、线面垂直、面面垂直之间可以相互转化,因此整个解题过程始终沿着线线垂直、线面垂直、面面垂直的转化途径进行. (3)求几何体的体积也常用转化法.如三棱锥顶点和底面的转化,几何体的高利用平行、中点,比例关系的转化等. (2019·郑州模拟)如图,在四棱锥PABCD中,△PAD是等腰直角三角形,且∠APD=90°,∠ABC=90°,AB∥CD,AB=2CD=2BC=8,平面PAD⊥平面ABCD,M是PC的三等分点(靠近C点处). (1)求证:平面MBD⊥平面PAD; (2)求三棱锥DMAB的体积. [解](1)证明:由题易得BD=AD=4, ∴AB2=AD2+BD2, ∴BD⊥AD. ∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,BD平面ABCD,∴BD⊥平面PAD. 又∵BD平面MBD,∴平面MBD⊥平面PAD. (2)过点P作PO⊥AD交AD于点O(图略),∵平面PAD⊥平面DAB,平面PAD∩平面DAB=AD,∴PO⊥平面DAB,∴点P到平面DAB的距离为PO=2. ∴VDMAB=VMDAB=S△DAB·PO=××(4)2××2=. 解答本例第(2)问时,利用比例关系求出点M到平面ABCD的距离. 已知边长为2的正方形ABCD与菱形ABEF所在平面互相垂直,M为BC中点. - 8 - (1)求证:EM∥平面ADF; (2)若∠ABE=60°,求四面体MACE的体积. [解](1)证明:∵四边形ABCD是正方形, ∴BC∥AD. ∵BC平面ADF,AD平面ADF, ∴BC∥平面ADF. ∵四边形ABEF是菱形, ∴BE∥AF. ∵BE平面ADF,AF平面ADF, ∴BE∥平面ADF. ∵BC∥平面ADF,BE∥平面ADF,BC∩BE=B, ∴平面BCE∥平面ADF. ∵EM平面BCE, ∴EM∥平面ADF. (2)取AB中点P,连接PE. ∵在菱形ABEF中,∠ABE=60°, ∴△AEB为正三角形,∴EP⊥AB. ∵AB=2,∴EP=. ∵平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB, ∴EP⊥平面ABCD, ∴EP为四面体EACM的高. ∴VMACE=VEACM=S△ACM·EP =××1×2×=. ⊙考点2 平面图形的翻折问题 解决平面图形翻折问题的步骤 - 8 - (2019·全国卷Ⅲ)图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°.将其沿AB,BC折起使得BE与BF重合,连接DG,如图2. 图1 图2 (1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE; (2)求图2中的四边形ACGD的面积. [解](1)证明:由已知得AD∥BE,CG∥BE,所以AD∥CG, 故AD,CG确定一个平面,从而A,C,G,D四点共面. 由已知得AB⊥BE,AB⊥BC,故AB⊥平面BCGE. 又因为AB平面ABC,所以平面ABC⊥平面BCGE. (2)取CG的中点M,连接EM,DM. 因为AB∥DE,AB⊥平面BCGE,所以DE⊥平面BCGE,故DE⊥CG. 由已知,四边形BCGE是菱形,且∠EBC=60°,得EM⊥CG, 故CG⊥平面DEM. 因此DM⊥CG. 在Rt△DEM中,DE=1,EM=, 故DM=2. 所以四边形ACGD的面积为4. (1)解答本例第(1)问的关键是折叠后AD∥BE,CG∥BE不变. (2)解答本例第(2)问的关键是,根据DE⊥平面BCGE,四边形BCGE是菱形找出四边形ACGD的高. [教师备选例题] 如图1,在平面五边形ABCDE中,AB∥CE,且AE=2,∠AEC=60°,CD=ED=,cos∠EDC=.将△CDE沿CE折起,使点D到P的位置,且AP=,得到如图2所示的四棱锥P - 8 - ABCE. 图1 图2 (1)求证:AP⊥平面ABCE; (2)记平面PAB与平面PCE相交于直线l,求证:AB∥l. [证明](1)在△CDE中, ∵CD=ED=,cos∠EDC=, 由余弦定理得 CE==2. 连接AC, ∵AE=2,∠AEC=60°, ∴AC=2. 又AP=, ∴在△PAE中,AP2+AE2=PE2,即AP⊥AE. 同理,AP⊥AC. ∵AC∩AE=A,AC平面ABCE,AE平面ABCE,∴AP⊥平面ABCE. (2)∵AB∥CE,且CE平面PCE,AB平面PCE,∴AB∥平面PCE. 又平面PAB∩平面PCE=l,∴AB∥l. (2019·济南模拟)如图1所示,在等腰梯形ABCD中,AB∥CD,∠BAD=45°,AB=2CD=4,点E为AB的中点.将△ADE沿DE折起,使点A到达P的位置,得到如图2所示的四棱锥PEBCD,点M为棱PB的中点. - 8 - 图1 图2 (1)求证:PD∥平面MCE; (2)若平面PDE⊥平面EBCD,求三棱锥MBCE的体积. [解](1)证明:在题图①中,∵BE=AB=CD, 且BE∥CD,∴四边形EBCD是平行四边形, 如图,连接BD,交CE于点O,连接OM,∴O是BD的中点,又点M是棱PB的中点, ∴OM∥PD,∵PD平面MCE,OM平面MCE,∴PD∥平面MCE. (2)在题图中,EBCD是平行四边形, ∴DE=BC, ∵四边形ABCD是等腰梯形, ∴AD=BC,∴AD=DE, ∵∠BAD=45°,∴AD⊥DE, 如图,PD⊥DE, 又平面PDE⊥平面EBCD,且平面PDE∩平面EBCD=DE, ∴PD⊥平面EBCD. 由(1)知OM∥PD, ∴OM⊥平面EBCD, 在等腰直角三角形ADE中,∵AE=2, ∴AD=DE=,∴OM=PD=AD=, ∵S△BCE=S△ADE=1, ∴三棱锥MBCE的体积 VMBCE=S△BCE·OM=. ⊙考点3 线面位置关系中的存在性问题 存在性问题的一般解题方法 先假设 - 8 - 其存在,然后把这个假设作为已知条件,和题目的其他已知条件一起进行推理论证和计算.在推理论证和计算无误的前提下,如果得到了一个合理的结论,则说明存在;如果得到了一个不合理的结论,则说明不存在.而对于探求点的问题,一般是先探求点的位置,多为线段的中点或某个三等分点,然后给出符合要求的证明. (2019·北京高考)如图,在四棱锥PABCD中,PA⊥平面ABCD,底面ABCD为菱形,E为CD的中点. (1)求证:BD⊥平面PAC; (2)若∠ABC=60°,求证:平面PAB⊥平面PAE; (3)棱PB上是否存在点F,使得CF∥平面PAE?说明理由. [解](1)证明:因为PA⊥平面ABCD, 所以PA⊥BD. 因为底面ABCD为菱形, 所以BD⊥AC. 又PA∩AC=A, 所以BD⊥平面PAC. (2)证明:因为PA⊥平面ABCD, AE平面ABCD, 所以PA⊥AE. 因为底面ABCD为菱形,∠ABC=60°,且E为CD的中点,所以AE⊥CD.所以AB⊥AE. 又AB∩PA=A,所以AE⊥平面PAB. 因为AE平面PAE,所以平面PAB⊥平面PAE. (3)棱PB上存在点F,使得CF∥平面PAE. 取PB的中点F,PA的中点G,连接CF,FG,EG, 则FG∥AB,且FG=AB. 因为底面ABCD为菱形,且E为CD的中点, 所以CE∥AB,且CE=AB. 所以FG∥CE,且FG=CE. 所以四边形CEGF为平行四边形.所以CF∥EG. 因为CF平面PAE,EG平面PAE, - 8 - 所以CF∥平面PAE. 解答本例第(3)问的难点在于如何探索出点F是PB的中点,可结合点E是CD的中点,CF∥平面PAE探求. [教师备选例题] 如图,在四棱锥PABCD中,PD⊥平面ABCD,底面ABCD为正方形,BC=PD=2,E为PC的中点,CB=3CG. (1)求证:PC⊥BC; (2)AD边上是否存在一点M,使得PA∥平面MEG?若存在,求出AM的长;若不存在,请说明理由. [解](1)证明:因为PD⊥平面ABCD,BC平面ABCD,所以PD⊥BC. 因为四边形ABCD是正方形,所以BC⊥CD. 又PD∩CD=D,PD平面PCD,CD平面PCD, 所以BC⊥平面PCD. 因为PC平面PCD,所以PC⊥BC. (2)连接AC,BD交于点O,连接EO,GO,延长GO交AD于点M,连接EM,则PA∥平面MEG. 证明如下:因为E为PC的中点,O是AC的中点, 所以EO∥PA. 因为EO平面MEG,PA平面MEG,所以PA∥平面MEG. 因为△OCG≌△OAM,所以AM=CG=,所以AM的长为. (2018·全国卷Ⅲ)如图,矩形ABCD所在平面与半圆弧所在平面垂直,M是上异于C,D的点. - 8 - (1)证明:平面AMD⊥平面BMC; (2)在线段AM上是否存在点P,使得MC∥平面PBD?说明理由. [解](1)证明:由题设知,平面CMD⊥平面ABCD,交线为CD.因为BC⊥CD,BC平面ABCD,所以BC⊥平面CMD,故BC⊥DM. 因为M为上异于C,D的点,且DC为直径,所以DM⊥CM. 又BC∩CM=C,所以DM⊥平面BMC. 而DM平面AMD, 故平面AMD⊥平面BMC. (2)当P为AM的中点时,MC∥平面PBD. 证明如下:如图,连接AC交BD于O. 因为ABCD为矩形,所以O为AC中点.连接OP,因为P为AM中点,所以MC∥OP.MC平面PBD,OP平面PBD,所以MC∥平面PBD. - 8 -查看更多