- 2021-05-10 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2021届高考数学一轮总复习课时作业54双曲线含解析苏教版
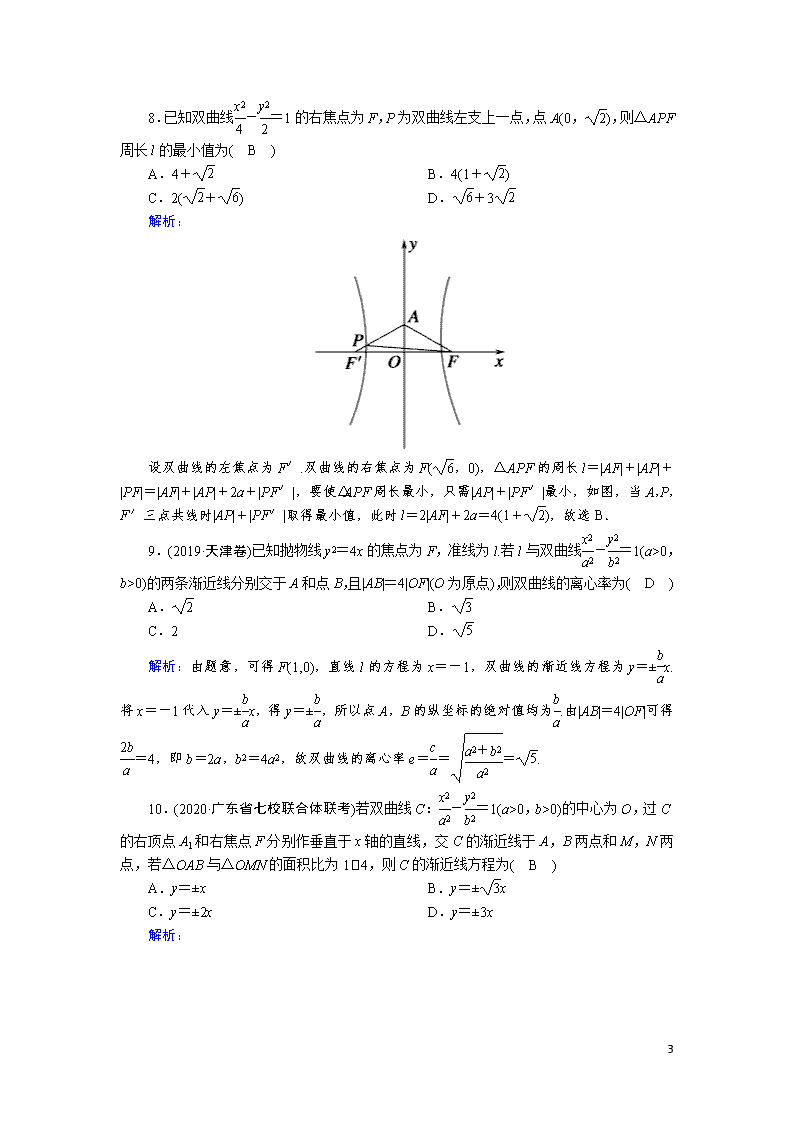
课时作业54 双曲线 一、选择题 1.已知双曲线-=1,则其焦距为( D ) A. B.2 C. D.2 解析:由双曲线方程知c2=9+4=13,∴c=,∴焦距为2,故选D. 2.(2019·北京卷)已知双曲线-y2=1(a>0)的离心率是,则a=( D ) A. B.4 C.2 D. 解析:解法1:由双曲线方程可知b2=1,所以c==,所以e===,解得a=,故选D. 解法2:由e=,e2=1+,b2=1,得5=1+,得a=,故选D. 3.已知双曲线-=1(m>0)的虚轴长是实轴长的2倍,则双曲线的标准方程为( D ) A.-=1 B.-=1 C.x2-=1 D.-=1 解析:由题意,得2=,解得m=2,∴双曲线的标准方程为-=1,故选D. 4.(2020·合肥市教学质量检测)已知双曲线-=1(a>0,b>0)的一条渐近线方程为y=2x,且经过点P(,4),则双曲线的方程是( C ) A.-=1 B.-=1 C.-=1 D.x2-=1 7 解析:因为双曲线的一条渐近线方程为y=2x,所以=2 ①.又双曲线过点P(,4),所以-=1 ②.①②联立,解得a=,b=2,所以双曲线的方程为-=1,故选C. 5.已知定点F1(-2,0),F2(2,0),N是圆O:x2+y2=1上任意一点,点F1关于点N的对称点为M,线段F1M的中垂线与直线F2M相交于点P,则点P的轨迹是( D ) A.直线 B.圆 C.椭圆 D.双曲线 解析:因为N为线段F1M的中点,O为线段F1F2的中点,所以|F2M|=2|ON|=2.因为P在线段F1M的中垂线上,所以|PF1|=|PM|,所以||PF1|-|PF2||=|F2M|=2|ON|=2<|F1F2|,所以点P的轨迹是双曲线,故选D. 6.(2019·全国卷Ⅲ)已知F是双曲线C:-=1的一个焦点,点P在C上,O为坐标原点.若|OP|=|OF|,则△OPF的面积为( B ) A. B. C. D. 解析:因为c2=a2+b2=9,所以|OP|=|OF|=3.设点P的坐标为(x,y),则x2+y2=9,把x2=9-y2代入双曲线方程得|y|=,所以S△OPF=|OF|·|yP|=.故选B. 7.(2020·洛阳市联考)经过点(2,1),且渐近线与圆x2+(y-2)2=1相切的双曲线的标准方程为( A ) A.-=1 B.-y2=1 C.-=1 D.-=1 解析:设双曲线的渐近线方程为y=kx,即kx-y=0,由渐近线与圆x2+(y-2)2=1相切可得圆心(0,2)到渐近线的距离等于半径1,由点到直线的距离公式可得=1,解得k=±.因为双曲线经过点(2,1),所以双曲线的焦点在x轴上,可设双曲线的方程为-=1(a>0,b>0),将点(2,1)代入可得-=1,由,得,故所求双曲线的方程为-=1.故选A. 8.已知双曲线-=1的右焦点为F,P为双曲线左支上一点,点A(0,),则△APF周长l的最小值为( B ) A.4+ B.4(1+) C.2(+) D.+3 解析: 7 设双曲线的左焦点为F′.双曲线的右焦点为F(,0),△APF的周长l=|AF|+|AP|+|PF|=|AF|+|AP|+2a+|PF′|,要使△APF周长最小,只需|AP|+|PF′|最小,如图,当A,P,F′三点共线时|AP|+|PF′|取得最小值,此时l=2|AF|+2a=4(1+),故选B. 9.(2019·天津卷)已知抛物线y2=4x的焦点为F,准线为l.若l与双曲线-=1(a>0,b>0)的两条渐近线分别交于A和点B,且|AB|=4|OF|(O为原点),则双曲线的离心率为( D ) A. B. C.2 D. 解析:由题意,可得F(1,0),直线l的方程为x=-1,双曲线的渐近线方程为y=±x.将x=-1代入y=±x,得y=±,所以点A,B的纵坐标的绝对值均为.由|AB|=4|OF|可得=4,即b=2a,b2=4a2,故双曲线的离心率e===. 10.(2020·广东省七校联合体联考)若双曲线C:-=1(a>0,b>0)的中心为O,过C的右顶点A1和右焦点F分别作垂直于x轴的直线,交C的渐近线于A,B两点和M,N两点,若△OAB与△OMN的面积比为14,则C的渐近线方程为( B ) A.y=±x B.y=±x C.y=±2x D.y=±3x 解析: 7 如图,因为AB∥MN,所以△OAB∽△OMN,又△OAB与△OMN的面积比为14,所以==,则a=c,所以b2=c2-a2=c2,则b=c,所以双曲线-=1(a>0,b>0)的渐近线方程为y=±x=±=±x,故选B. 11.(2020·石家庄教学质量检测)已知双曲线-=1(a>0,b>0)的左、右焦点分别为F1,F2,点A为双曲线右支上一点,线段AF1交左支于点B,若AF2⊥BF2,且|BF1|=|AF2|,则该双曲线的离心率为( B ) A. B. C. D.3 解析:设|AF2|=x,∵点A在双曲线的右支上, ∴|AF1|=2a+x.∵|BF1|=,∴|BF1|=, ∴|AB|=2a+.∵点B在双曲线的左支上, ∴|BF2|=2a+.∵AF2⊥BF2, ∴(2a+)2-(2a+)2=x2,化简得x=2a, ∴|AF1|=4a,|AB|=a,∴cos∠BAF2=.在△AF1F2中,由余弦定理得|AF1|2+|AF2|2-2|AF1||AF2|cos∠BAF2=|F1F2|2,即16a2+4a2-2×4a×2a×=4c2,即13a2=5c2,∴=,∴双曲线的离心率为,故选B. 12.(2020·贵阳市监测考试)已知点F是双曲线C:-=1(a>0,b>0)的左焦点,点E是该双曲线的右顶点,过F且垂直于x轴的直线与双曲线交于A,B两点,若△ABE是钝角三角形,则该双曲线的离心率的取值范围是( B ) A.(1,2) B.(2,+∞) C.(1,3] D.[3,+∞) 解析:根据双曲线的对称性,可知∠AEF>可使△ABE为钝角三角形,即>a+c⇒b2>a2+ac⇒c2>2a2+ac⇒e2-e-2>0(e>1),所以e>2,选B. 二、填空题 13.(2019·江苏卷)在平面直角坐标系xOy中,若双曲线x2-=1(b>0)经过点(3,4),则该双曲线的渐近线方程是y=±x. 7 解析:因为双曲线x2-=1(b>0)经过点(3,4),所以9-=1,得b=,所以该双曲线的渐近线方程是y=±bx=±x. 14.(2020·石家庄模拟)已知双曲线C:x2-4y2=1,过点P(2,0)的直线l与C有唯一公共点,则直线l的方程为y=±(x-2). 解析:∵双曲线C的方程为x2-4y2=1,∴a=1,b=,∴渐近线方程为y=±x.∵P(2,0)在双曲线内部且直线l与双曲线有唯一公共点,∴直线l与双曲线的渐近线平行,∴直线l的斜率为±,∴直线l的方程为y=±(x-2). 15.(2020·昆明市诊断测试)已知点P(1,)在双曲线C:-=1(a>0,b>0)的渐近线上,F为C的右焦点,O为原点,若∠FPO=90°,则C的方程为-=1. 解析:设双曲线的一条渐近线方程为y=x,由渐近线过点P(1,),得=,且|OP|=2.焦点到渐近线的距离是b,即|PF|=b,在Rt△OPF中,|OF|2=|OP|2+|PF|2,即c2=22+b2.又c2=a2+b2,所以a=2,b=2,所以双曲线C的方程为-=1. 16.(2020·济南市质量评估)古希腊数学家阿波罗尼斯在他的著作《圆锥曲线论》中记截了用平面切割圆锥得到圆锥曲线的方法.如图,将两个完全相同的圆锥对顶放置(两圆锥的轴重合),已知两个圆锥的底面半径均为1,母线长均为2,记过圆锥轴的平面ABCD为平面α(α与两个圆锥侧面的交线为AC,BD),用平行于α的平面截圆锥,该平面与两个圆锥侧面的交线即双曲线Γ的一部分,且双曲线Γ的两条渐近线分别平行于AC,BD,则双曲线Γ的离心率为( A ) A. B. C. D.2 7 解析:设与平面α平行的平面为β,以AC,BD的交点在平面β内的射影为坐标原点,两圆锥的轴在平面β内的射影为x轴,在平面β内与x轴垂直的直线为y轴,建立平面直角坐标系.根据题意可设双曲线Γ:-=1(a>0,b>0).由题意可得双曲线Γ的渐近线方程为y=±x,即=,所以离心率e===. 17.(2020·济南市模拟)已知一族双曲线En:x2-y2=(n∈N*,且n≤2 019),设直线x=2与En在第一象限内的交点为An,点An在En的两条渐近线上的射影分别为Bn,Cn.记△AnBnCn的面积为an,则a1+a2+a3+…+a2 019=. 解析:因为双曲线的方程为x2-y2=(n∈N*,且n≤2 019),所以其渐近线方程为y=±x,设点An(2,yn),则4-y=(n∈N*,且n≤2 019). 记An(2,yn)到两条渐近线的距离分别为d1,d2,则S△AnBnCn=d1d2=××===,故an=,因此{an}为等差数列,故a1+a2+a3+…+a2 019=×2 019+×=. 18.已知双曲线C:-=1(a>0,b>0)的左、右焦点分别为F1,F2,渐近线方程是y=±x,点A(0,b),且△AF1F2的面积为6. (1)求双曲线C的标准方程; (2)直线l:y=kx+m(k≠0,m≠0)与双曲线C交于不同的两点P,Q,若|AP|=|AQ|,求实数m的取值范围. 解:(1)由题意得=①,S△AF1F2=×2c·b=6②,a2+b2=c2③, 由①②③求得a2=5,b2=4, ∴双曲线C的标准方程是-=1. (2)设P(x1,y1),Q(x2,y2),线段PQ的中点为D(x0,y0).将y=kx+m与-=1联立,消去y,整理得(4-5k2)x2-10kmx-5m2-20=0,由4-5k2≠0及Δ>0, 得④ ∴x1+x2=,x1·x2=-, ∴x0==,y0=kx0+m=. 7 由|AP|=|AQ|知,AD⊥PQ,∴kAD===-,化简得10k2=8-9m,⑤ 将⑤代入④,得m<-或m>0. 由10k2=8-9m>0,得m<. 综上,实数m的取值范围是m<-或0查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档