八年级数学上册第十二章全等三角形专题课堂二证明三角形全等的基本类型课件新版 人教版

八年级数学上册第十二章全等三角形专题课堂二证明三角形全等的基本类型课件新版 人教版

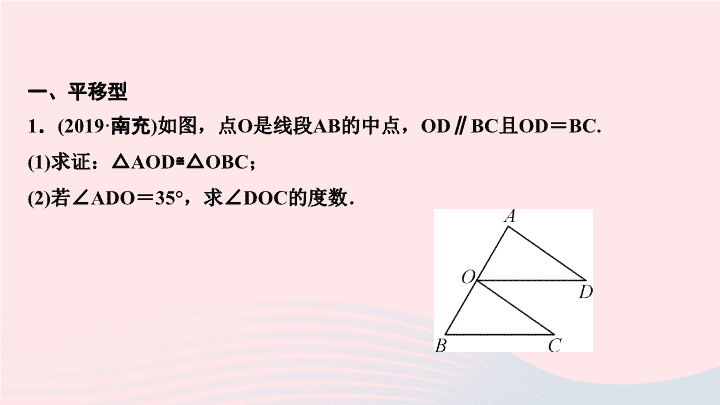
第十二章　全等三角形 专题课堂(二)　证明三角形全等的基本类型 一、平移型 1 ． (2019 · 南充 ) 如图，点 O 是线段 AB 的中点， OD∥BC 且 OD ＝ BC. (1) 求证：△ AOD≌△OBC ； (2) 若∠ ADO ＝ 35° ，求∠ DOC 的度数． 二、翻折型 2 ．如图，在△ ABC 与△ DCB 中， AC 与 BD 相交于点 E ，且∠ A ＝∠ D ， AB ＝ DC. (1) 求证：△ ABE≌△DCE ； (2) 当∠ AEB ＝ 50° ，求∠ EBC 的度数． 3 ．如图，点 C ， E 分别为△ ABD 的边 BD ， AB 上两点，且 AE ＝ AD ， CE ＝ CD ，∠ D ＝ 70° ，∠ ECD ＝ 150° ，求∠ B 的度数． 解：连接 AC ，∵ AE ＝ AD ， CE ＝ CD ， AC ＝ AC ，∴△ ACE≌△ACD ，∴∠ AEC ＝∠ D ＝ 70° ，又∵∠ ECD ＝ 150° ，∴∠ ECB ＝ 30° ，∴∠ B ＝ 70° － 30° ＝ 40° 三、旋转型 4 ．如图， AB⊥DC 于点 B ，且 BD ＝ BA ， BE ＝ BC ，延长 DE ，交 AC 于点 F. 求证： DE ＝ AC ，且 DE⊥AC. 四、 “ K ” 字型 5 ．如图， AD⊥AB 于点 A ， BE⊥AB 于点 B ， C 为 AB 上一点，且 CD⊥CE ， CD ＝ CE. 求证： AB ＝ AD ＋ BE. 解：∵ AD⊥AB ， BE⊥AB ，∴∠ A ＝∠ B ＝ 90° ，∠ D ＋∠ DCA ＝ 90° ，又∵ DC⊥EC ，∴∠ ECB ＋∠ DCA ＝ 90° ，∴∠ D ＝∠ ECB ，由 AAS 可证△ ACD≌△BEC ，∴ AD ＝ BC ， AC ＝ BE ，∵ AB ＝ BC ＋ AC ，∴ AB ＝ AD ＋ BE