数学冀教版八年级上册教案13-3全等三角形的判定（3）

数学冀教版八年级上册教案13-3全等三角形的判定（3）

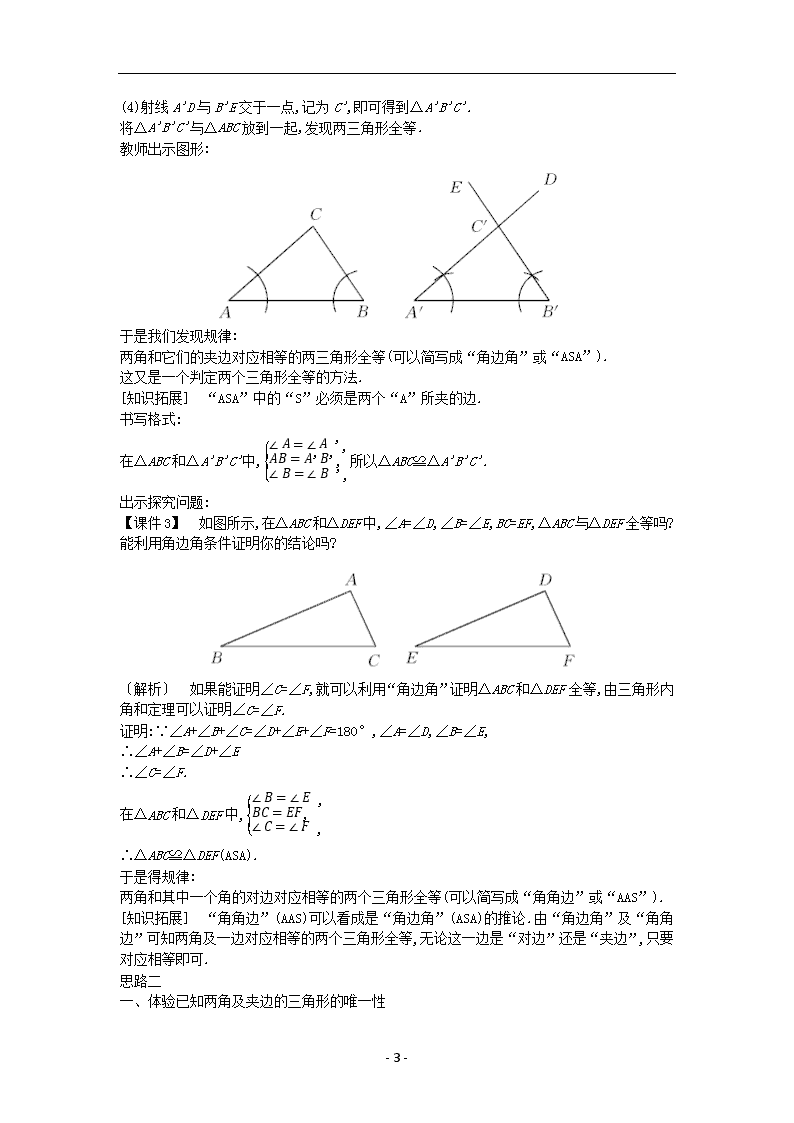
- 1 - 13.3 全等三角形的判定（3） 教学目标 【知识与能力】 1.掌握“角边角”及“角角边”的内容. 2.能初步应用“角边角”及“角角边”判定两个三角形全等. 【过程与方法】 使学生经历探索三角形全等的过程,体验用操作、归纳得出数学结论的过程. 【情感态度价值观】 通过探究三角形全等的活动,培养学生敢于面对困难、克服困难的能力. 教学重难点 【教学重点】 “角边角”及“角角边”的内容. 【教学难点】 分析问题,寻找判定两个三角形全等的条件. 课前准备 多媒体课件 教学过程 一、新课导入： 导入一: 教师讲解:前面,我们已经知道,当两个三角形的两条边及其夹角分别对应相等时,两个三角 形一定全等,而当两个三角形的两条边及其中一边的对角分别对应相等时,两个三角形不一 定全等. 这节课,我们将讨论以下情况:如图所示,一种情况是已知两个角及这两角的夹边;另一种情 况是已知两个角及其中一角的对边. [设计意图] 让学生明确本节课要研究的主要内容,并明确三角形中边与角的位置关系,理 - 2 - 解“两角夹一边”和“两角一对边”的含义. 导入二: 1.复习旧知: (1)三角形中已知三个元素,包括哪几种情况? (三个角、三个边、两边一角、两角一边) (2)到目前为止,可以作为判定两三角形全等的方法有几种?各是什么? 2.师:在三角形中,已知三个元素的四种情况中,我们研究了两种,我们接着探究已知两角一 边是否可以判定两三角形全等. 导入三: 【课件 1】 如图所示,小明不小心把一块三角形的玻璃打碎成四块,现在要去玻璃店配一块 完全一样的玻璃,那么最省事的办法是什么?你能帮小明出出主意吗? 要想最省事,就要带块数最少且要满足它能够确定该三角形的形状和大小,这就是本节课要 学到的判定三角形全等的知识.学完本节,你就会知道为什么应该带第 2 块去. [设计意图] 激趣设疑,让学生产生学习的兴趣,积极地投入到本节课的学习之中. 二、新知构建： [过渡语] 在两角一边中有两种情况,下面我们就来研究这两种情况,即两角一夹边,两 角一对边. 活动一:“角边角”基本事实和“角角边”定理的探究 思路一 做一做: 【课件 2】 三角形的两个内角分别是 60°和 80°,它们的夹边为 4 cm,你能画一个三角形 同时满足这些条件吗?将你画的三角形剪下来. 同伴比较,观察它们是不是全等,你能得出什么结论? 【学生活动】 自己动手操作,然后与同伴交流,得出结论. 【教师活动】 检查指导,帮助有困难的同学. 活动结果展示: 以小组为单位将所得三角形放在一起,发现完全重合,这说明这些三角形全等. 提炼结论: 两角和它们的夹边对应相等的两个三角形全等(可以简记为“角边角”或“ASA”). 师:我们刚才作的三角形是一个特殊三角形,随意画一个三角形 ABC,能不能作一个ΔA'B'C', 使∠A=∠A',∠B=∠B',AB=A'B'呢? 生:能. 学生口述画法,教师进行多媒体课件演示,使学生加深对“ASA”的理解. 生:(1)先用量角器量出∠A 与∠B 的度数,再用直尺量出 AB 边的长; (2)画线段 A'B',使 A'B'=AB; (3)分别以 A',B'为顶点,A'B'为一边在同侧作∠DA'B',∠EB'A',使∠DA'B'=∠CAB,∠ EB'A'=∠CBA; - 3 - (4)射线 A'D 与 B'E 交于一点,记为 C',即可得到ΔA'B'C'. 将ΔA'B'C'与ΔABC 放到一起,发现两三角形全等. 教师出示图形: 于是我们发现规律: 两角和它们的夹边对应相等的两三角形全等(可以简写成“角边角”或“ASA”). 这又是一个判定两个三角形全等的方法. [知识拓展] “ASA”中的“S”必须是两个“A”所夹的边. 书写格式: 在ΔABC 和ΔA'B'C'中, ∠ = ∠ ', = ' ', ∠ = ∠ ', 所以ΔABC≌ΔA'B'C'. 出示探究问题: 【课件 3】 如图所示,在ΔABC 和ΔDEF 中,∠A=∠D,∠B=∠E,BC=EF,ΔABC 与ΔDEF 全等吗? 能利用角边角条件证明你的结论吗? 〔解析〕 如果能证明∠C=∠F,就可以利用“角边角”证明ΔABC 和ΔDEF 全等,由三角形内 角和定理可以证明∠C=∠F. 证明:∵∠A+∠B+∠C=∠D+∠E+∠F=180°,∠A=∠D,∠B=∠E, ∴∠A+∠B=∠D+∠E ∴∠C=∠F. 在ΔABC 和ΔDEF 中, ∠ = ∠ , = , ∠ = ∠ , ∴ΔABC≌ΔDEF(ASA). 于是得规律: 两角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”). [知识拓展] “角角边”(AAS)可以看成是“角边角”(ASA)的推论.由“角边角”及“角角 边”可知两角及一边对应相等的两个三角形全等,无论这一边是“对边”还是“夹边”,只要 对应相等即可. 思路二 一、体验已知两角及夹边的三角形的唯一性 - 4 - 1.利用刻度尺、量角器、小刀等工具制作符合如下条件的三角形: (1)ΔABC,其中∠A=35°,∠B=65°,AB=5 cm; (2)ΔDEF,其中∠D=70°,∠E=50°,∠E 的对边 DF=4 cm. 注意:(2)题学生可能感觉难度较大,教师可提示学生先求出∠F=60°,再利用(1)的作法进行 作图. 2.如果“两角及一边”条件中的边是两角所夹的边,那么你画的三角形与同伴画的一定完全 重合吗?试试看. 结论:有两角和夹边对应相等的两个三角形全等,简写成“ASA”或“角边角”. 3.如果“两角及一边”条件中的边是其中一角的对边,以你所画的ΔDEF 为例,你画的三角形 与同伴画的一定完全重合吗?试试看. 结论:有两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”. 二、证明“ASA”定理 教师出示已知条件:如图所示,在ΔABC 和ΔA'B'C'中,已知 AB=A'B',∠A=∠A',∠B=∠B'.求 证ΔABC≌ΔA'B'C'. 教师给出证明方法:由于 AB=A'B',我们移动其中的ΔABC,使点 A 与点 A'、点 B 与点 B'重合, 且使点 C 与点 C'分别位于线段 AB,A'B'的同侧,因为∠A=∠A',因此可以使∠A 与∠A'的边 AC 与 A'C'重叠在一起;同样因为∠B=∠B',可以使∠B 与∠B'的边 BC 与 B'C'重叠在一起,由于 两条直线相交只有一个交点,因此点 C 与点 C'重合,这就说明这两个三角形全等,由此可得判 定三角形全等的又一种简便方法: 如果两个三角形的两个角和它们的夹边对应相等,那么这两个三角形全等,简记为“ASA”(或 角边角). 三、证明“AAS”定理 教师出示应用“ASA”证明三角形全等的问题: 【 课 件 4 】 如 图 所 示 , 已 知 ∠ ABC= ∠ DCB, ∠ A= ∠ D, 求 证 Δ ABC ≌ Δ DCB. 教师要求学生应用“ASA”定理证明本题,学生思考后教师提问,并根据学生的回答加以引导 后由教师板书. 证明结束后教师提出问题:如果两个三角形有两个角及其中一个角的对边分别对应相等,那 么这两个三角形是否一定全等? 教师要求学生思考这个问题,并提醒学生利用三角形内角和为 180°这一公理来考虑问题, 一般学生都会得出正确结论,教师再加以总结:因为三角形的内角和为 180°,所以有两个角 - 5 - 对应相等,那么第三个角必对应相等,于是问题就由“角角边”转化为“角边角”,这样便可 证得这两个三角形全等. 教师要求学生自己证明“AAS”定理:如果两个三角形的两角及其中一个角的对边对应相等, 那么这两个三角形全等.简记为“AAS”(或角角边). 学生证明后,教师边讲解边板书. 教师提问:我们已经讨论了两个三角形有两边一角以及两角一边分别对应相等,这两个三角 形能否全等的情况.我们很容易发现,如果两个三角形有三个角分别对应相等,那么这两个三 角形未必全等,如图所示,这两个三角形三个角分别相等,它们并不全等,只是形状相同. 活动二:例题讲解 【课件 5】 已 知 : 如 图 所 示 ,AD=BE, ∠ A= ∠ FDE,BC ∥ EF. 求 证 : Δ ABC ≌ Δ DEF. [师生共析] 根据 AD=BE,得到 AB=DE;由两直线平行,得到同位角相等,然后利用“ASA”即可 得到ΔABC≌ΔDEF. 证明:∵AD=BE(已知), ∴AB=DE(等式的性质). ∵BC∥EF(已知), ∴∠ABC=∠E(两直线平行,同位角相等). 在ΔABC 和ΔDEF 中, ∵ ∠ = ∠ t , = t , ∠ = ∠ , ∴ΔABC≌ΔDEF(ASA). 师:到目前为止,在三角形中已知三个条件探索两个三角形全等的问题已全部结束,请同学们 把两个三角形全等的判定方法作一个小结. 【学生活动】 自我回忆总结,然后小组讨论交流、补充. 三、课堂小结： 知识点一:“角边角”判定三角形全等 两角和它们的夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”. 这是我们学习的第三个判定三角形全等的方法,这里的两角和夹边,是指同一个三角形的边 和角,边是两个角的夹边. 知识点二:“角角边”判定三角形全等 - 6 - 两角和其中一个角的对边分别相等的两个三角形全等(简写成“角角边”或“AAS”). 该判定是通过“ASA”推导得出的,今后可以直接用“AAS”来判定两个三角形全等,它是“ASA” 的一个推论.