- 2021-05-08 发布 |
- 37.5 KB |
- 3页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学人教版八年级上册教案14-1整式的乘法(第6课时)
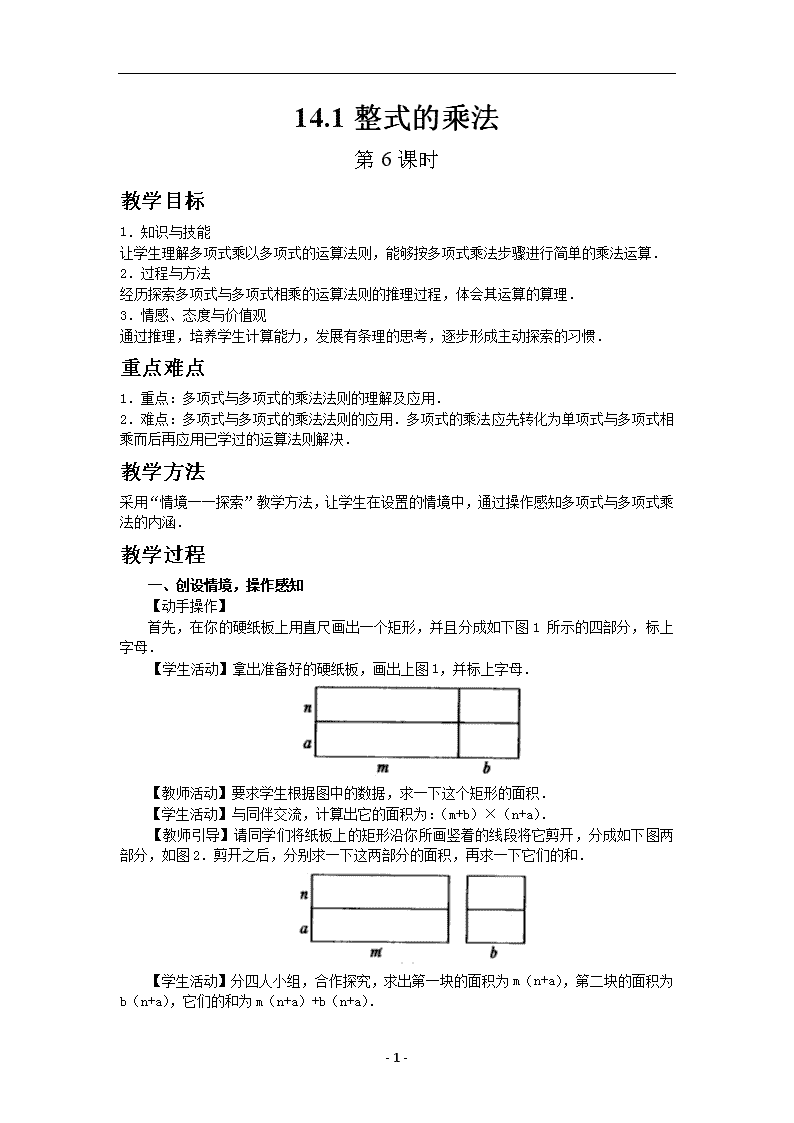
- 1 - 14.1 整式的乘法 第 6 课时 教学目标 1.知识与技能 让学生理解多项式乘以多项式的运算法则,能够按多项式乘法步骤进行简单的乘法运算. 2.过程与方法 经历探索多项式与多项式相乘的运算法则的推理过程,体会其运算的算理. 3.情感、态度与价值观 通过推理,培养学生计算能力,发展有条理的思考,逐步形成主动探索的习惯. 重点难点 1.重点:多项式与多项式的乘法法则的理解及应用. 2.难点:多项式与多项式的乘法法则的应用.多项式的乘法应先转化为单项式与多项式相 乘而后再应用已学过的运算法则解决. 教学方法 采用“情境──探索”教学方法,让学生在设置的情境中,通过操作感知多项式与多项式乘 法的内涵. 教学过程 一、创设情境,操作感知 【动手操作】 首先,在你的硬纸板上用直尺画出一个矩形,并且分成如下图 1所示的四部分,标上 字母. 【学生活动】拿出准备好的硬纸板,画出上图 1,并标上字母. 【教师活动】要求学生根据图中的数据,求一下这个矩形的面积. 【学生活动】与同伴交流,计算出它的面积为:(m+b)×(n+a). 【教师引导】请同学们将纸板上的矩形沿你所画竖着的线段将它剪开,分成如下图两 部分,如图 2.剪开之后,分别求一下这两部分的面积,再求一下它们的和. 【学生活动】分四人小组,合作探究,求出第一块的面积为 m(n+a),第二块的面积为 b(n+a),它们的和为 m(n+a)+b(n+a). - 2 - 【教师活动】组织学生继续沿着横的线段剪开,将图形分成四部分,如图 3,然后再 求这四块长方形的面积. 【学生活动】分四人小组合作学习,求出 S1=mn;S2=nb;S3=am;S4=ab,它们的和为 S=mn+nb+am+ab. 【教师提问】依据上面的操作,求得的图形面积,探索(m+b)(n+a)应该等于什么? 【学生活动】分四人小组讨论,并交流自己的看法. (m+b)×(n+a)=m(n+a)+b(n+a)=mn+nb+am+ab,因为我们三次计算是按照不同的 方法对同一个矩形的面积进行了计算,那么,两次的计算结果应该是相同的,所以(m+b) ×(n+a)=m(n+a)+b(n+a)=mn+nb+am+ab. 【师生共识】多项式与多项式相乘,用第一个多项式的每一项乘以另一个多项式的每一 项,再把所得的结果相加. 字母呈现: =ma+mb+na+nb. 二、范例学习,应用所学 【例 1】计算: (1)(x+2)(x-3) (2)(3x-1)(2x+1) 【例 2】计算: (1)(x-3y)(x+7y) (2)(2x+5y)(3x-2y) 【例 3】先化简,再求值: (a-3b)2+(3a+b)2-(a+5b)2+(a-5b)2,其中 a=-8,b=-6. 【教师活动】例 1~例 3,启发学生参与到例题所设置的计算问题中去. 【学生活动】参与其中,领会多项式乘法的运用方法以及注意的问题. 三、随堂练习,巩固新知 课本 P102 练习第 1、2 题. 【探究时空】 一块长 m 米,宽 n 米的玻璃,长宽各裁掉 a米后恰好能铺盖一张办公桌台面(玻璃与 台面一样大小),问台面面积是多少? 四、课堂总结,发展潜能 1.多项式与多项式相乘,应充分结合导图中的问题来理解多项式与多项式相乘的结果, 利用乘法分配律来理解(m+n)与(a+b)相乘的结果,导出多项式乘法的法则. 2.多项式与多项式相乘,第一步要先进行整理,在用一个多项式的每一项去乘另一个 多项式的每一项时,要“依次”进行,不重复,不遗漏,且各个多项式中的项不能自乘,多 项式是几个单项式的和,每一项都包括前面的符号,在计算时要正确确定积中各项的符号. 五、布置作业,专题突破 课本 P105 习题 14.1 第 5、6、7(2)、9、10 题. 板书设计 - 3 - 14.1.4 整式的乘法(3) 1、多项式乘以多项式的乘法法则 例: 练习:查看更多