高三数学(理数)总复习练习专题四 函数的图象、函数的应用
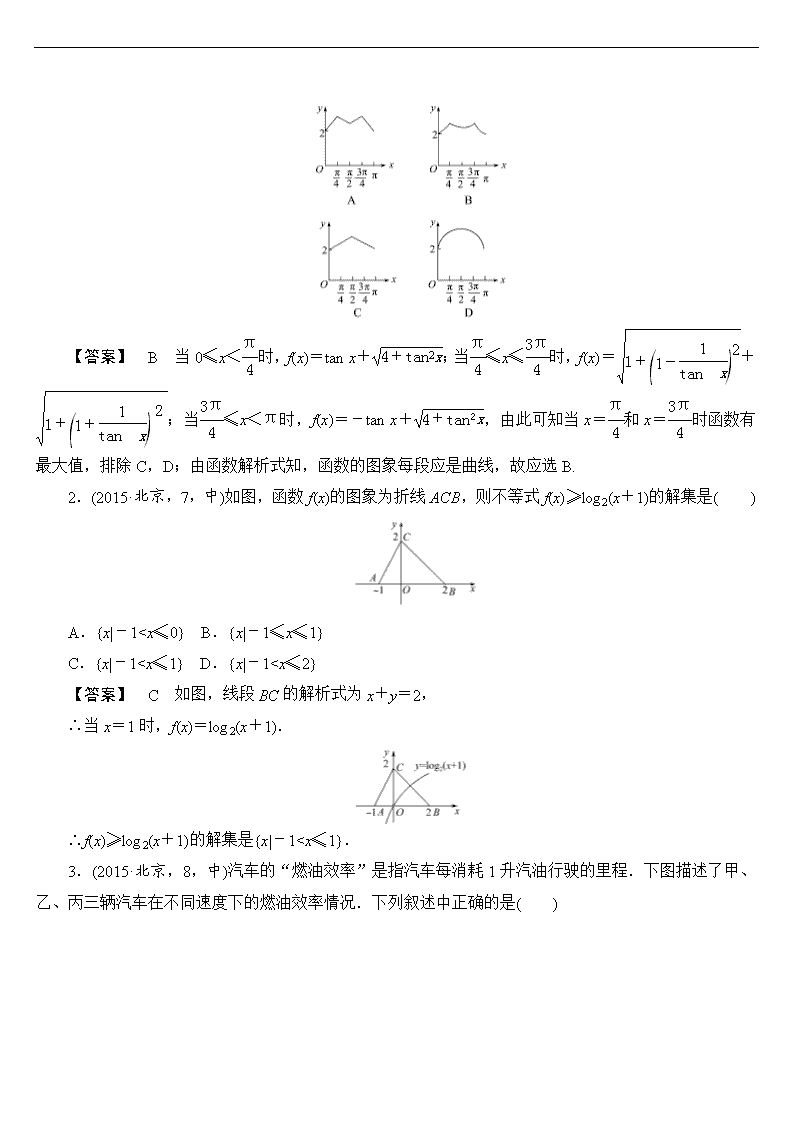
1.(2015·课标Ⅱ,10,中)如图,长方形ABCD的边AB=2,BC=1,O是AB的中点.点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为( )
【答案】 B 当0≤x<时,f(x)=tan x+;当≤x≤时,f(x)=+;当≤x<π时,f(x)=-tan x+,由此可知当x=和x=时函数有最大值,排除C,D;由函数解析式知,函数的图象每段应是曲线,故应选B.
2.(2015·北京,7,中)如图,函数f(x)的图象为折线ACB,则不等式f(x)≥log2(x+1)的解集是( )
A.{x|-1
0;
当x>0时,g′(x)<0,∴g(x)max=g(0)=0.
∴f(x)<0,排除A,C.又由f(x)的定义域为{x|x≠0},可排除D,故选B.
3.(2013·安徽,8,中)函数y=f(x)的图象如图所示,在区间[a,b]上可找到n(n≥2)个不同的数x1,x2,…,xn,使得==…=,则n的取值范围是( )
A.{3,4} B.{2,3,4} C.{3,4,5} D.{2,3}
【答案】 B ==…=,即y=f(x)的图象与y=kx的交点的坐标满足上述等式.又交点至少要有两个,至多有四个,故n可取2,3,4.
4.(2013·江西,10,难)如图,半径为1的半圆O与等边三角形ABC夹在两平行线l1,l2之间,l∥l1,l与半圆相交于F,G两点,与三角形ABC两边相交于E,D两点.设弧的长为x(00
B.当a<0时,x1+x2>0,y1+y2<0
C.当a>0时,x1+x2<0,y1+y2<0
D.当a>0时,x1+x2>0,y1+y2>0
【答案】 B 方法一:由题意知满足条件的两函数图象只有图(1)与图(2)两种情况,
图(1)中,作B关于原点的对称点B′,据图可知:当a<0时,x1+x2>0,y1+y2<0,故B正确.
图(2)中,作A关于原点的对称点A′,据图可知:当a>0时,x1+x2<0,y1+y2>0,C,D均错.
方法二:=ax2+bx⇔=ax+b,
分别作出y=和y=ax+b的图象,如下:
不妨设x1<0,x2>0,
当a>0时,x1+x2<0,
y1+y2=+=>0.
当a<0时,x1+x2>0,y1+y2=+=<0.故选B.
7.(2012·福建,10,难)函数f(x)在[a,b]上有定义,若对任意x1,x2∈[a,b],有f≤[f(x1)+f(x2)],则称f(x)在[a,b]上具有性质P.设f(x)在[1,3]上具有性质P,现给出如下命题:
①f(x)在[1,3]上的图象是连续不断的;
②f(x2)在[1,]上具有性质P;
③若f(x)在x=2处取得最大值1,则f(x)=1,x∈[1,3];
④对任意x1,x2,x3,x4∈[1,3],有f≤[f(x1)+f(x2)+f(x3)+f(x4)].
其中真命题的序号是( )
A.①② B.①③ C.②④ D.③④
【答案】 D 令f(x)=如图,f(x)在x∈[1,3]上具有性质P,可在x=3处不连续,①错;
令f(x)=-x,x∈[1,3],经检验可知f(x)=-x在x∈[1,3]上具有性质P.而f(x2)=-x2,x∈[1,],令g(x)=-x2,其图象如图所示.
由图象可知,g为点S的纵坐标,[g(x1)+g(x2)]为点F的纵坐标(其中EF为梯形ABCD
的中位线),∴由图可知g>[g(x1)+g(x2)],
∴②错.
设x∈[1,3],则4-x∈[1,3],
∴f(x)+f(4-x)≥2f
=2f(2)=2.
而f(x)+f(4-x)≤1+1=2,f(x)≤1,f(4-x)≤1,∴f(x)=f(4-x)=1,故③正确.
f
=f
≤
≤
=[f(x1)+f(x2)+f(x3)+f(x4)],
∴④正确.故真命题为③④.
考向1 函数图象的辨识
1.图象的变换
(1)平移变换
①y=f(x±a)(a>0)的图象,可由y=f(x)的图象沿x轴方向向左(+a)或向右(-a)平移 a个单位得到;
②y=f(x)±b(b>0)的图象,可由y=f(x)的图象沿y轴方向向上(+b)或向下(-b)平移 b个单位得到.
(2)对称变换
①y=f(-x)与y=f(x)的图象关于y轴对称;
②y=-f(x)与y=f(x)的图象关于x轴对称;
③y=-f(-x)与y=f(x)的图象关于原点对称.
(3)伸缩变换
①y=kf(x)(k>0)的图象,可由y=f(x)的图象上每一个点的纵坐标伸长(k>1)或缩短(00)的图象,可由y=f(x)的图象上每一个点的横坐标伸长(01)为原来的而得到.
(4)翻折变换
①要得到y=|f(x)|的图象,可先画出y=f(x)的图象,然后“上不动,下翻上”即可得到;
②由于y=f(|x|)是偶函数,要得到y=f(|x|)的图象,可先画出y=f(x)的图象,然后“右不动,左去掉,右翻左”即可得到.
进行图象变换时,要合理选择变换的顺序,并进行适当的转化变形.例如,要得到y=2-|x-1|的图象,由于y=2-|x-1|=,可将y=的图象先通过对称翻折得到y=的图象,再通过平移得到y=的图象.
2.利用函数的性质确定函数图象的一般步骤
(1)确定函数的定义域;
(2)化简函数的解析式;
(3)讨论函数的性质(奇偶性、单调性、周期性等)和图象上的特殊点线(如渐近线、对称轴等);
(4)利用基本函数的图象确定所给函数的图象.
(1)(2013·四川,7)函数y=的图象大致是( )
(2)(2014·课标Ⅰ,6)如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,过点P作直线OA的垂线,垂足为M,将点M到直线OP的距离表示成x的函数f(x),则y=f(x)在[0,π]上的图象大致为( )
【解析】 (1)(排除法)由已知得,3x-1≠0⇒x≠0,排除A;
又∵x<0时,3x-1<0,x3<0,∴y=>0,故排除B;
又y′=,当3-xln 3<0时,x>>0,y′<0,所以D不符合.
(2)(排除法)由题图可知:当x=时,OP⊥OA,此时f(x)=0,排除A,D;当x∈时,OM=cos x,设点M到直线OP的距离为d,则=sin x,即d=OMsin x=sin x·cos x,∴f(x)=sin xcos x=sin 2x≤,排除B,故选C.
【答案】 (1)C (2)C
【点拨】 解答此类问题时注意函数的奇偶性、单调性、极值、特殊点处的函数值.
辨识函数图象的两种方法
(1)直接根据函数解析式作出函数图象,或者是根据图象变换作出函数的图象;
(2)利用间接法,排除、筛选错误与正确的选项,可以从如下几个方面入手:
①从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置;
②从函数的单调性,判断图象的变化趋势;
③从函数的奇偶性,判断图象的对称性:如奇函数在对称的区间上单调性一致,偶函数在对称的区间上单调性相反;
④从函数的周期性,判断图象的循环往复;
⑤从特殊点出发,排除不符合要求的选项.
灵活应用上述方法,可以很快判断出函数的图象.
(2013·山东,8)函数y=xcos x+sin x的图象大致为( )
【答案】 D 方法一:令f(x)=xcos x+sin x,
∵f(-x)=-x·cos x-sin x=-f(x),
∴函数y=xcos x+sin x为奇函数,可排除B.
令xcos x+sin x=0,得tan x=-x,在同一直角坐标系中画出函数y=tan x和y=-x的图象如图,由图可知函数y=xcos x+sin x的零点有一个介于到π之间,可排除A,C,故选D.
方法二:令f(x)=xcos x+sin x,则有f(-x)=-xcos x-sin x=-f(x),
∴f(x)为奇函数.∵奇函数的图象关于原点对称,而B中图象不关于原点对称,∴排除B;当x=时,y=1,而由C中图象知当x=时,y≠1,∴排除C;当x=π时,y=-π,而A中,当x=π时,y>0,∴排除A,故选D.
考向2 函数图象的应用
利用函数图象研究的几个方面
(1)利用函数的图象研究函数的性质:①从图象的最高点、最低点,分析函数的最值、极值;②从图象的对称性,分析函数的奇偶性;③从图象的走向趋势,分析函数的单调性、周期性.
(2)利用函数的图象研究不可解方程的根的个数、求不等式的解集以及求参数的取值范围等.
(1)(2011·课标全国,12)已知函数y=f(x)的周期为2,当x∈[-1,1]时,f(x)=x2,那么函数y=f(x)的图象与函数y=|lg x|的图象的交点共有( )
A.10个 B.9个 C.8个 D.1个
(2)(2014·山东,8)已知函数f(x)=|x-2|+1,g(x)=kx.若方程f(x)=g(x)有两个不相等的实根,则实数
k的取值范围是( )
A. B.
C.(1,2) D.(2,+∞)
【解析】 (1)在同一平面直角坐标系中分别作出y=f(x)和y=|lg x|的图象,如图.又lg 10=1,由图象知选A.
(2)f(x)=如图,作出y=f(x)的图象,其中A(2,1),则kOA=.
要使方程f(x)=g(x)有两个不相等的实根,则函数f(x)与g(x)的图象有两个不同的交点,由图可知,1时与直线y=x+1平行,此时有一个公共点,∴k∈(0,1)∪(1,4)时,两函数图象恰有两个交点.
【答案】 (0,1)∪(1,4)
1.(2015·湖南株洲一模,6)函数y=xsin x在[-π,π]上的图象是( )
【答案】 A 函数y=xsin x是偶函数,所以其图象关于y轴对称,排除D;由x=π时,y=0,排除C;由x=时,y=,排除B,故选A.
2.(2015·福建三明调研,3)函数y=ax2+bx与函数y=xa+b(a≠0)在同一坐标系中的图象可能为( )
【答案】 C y=ax2+bx=a-.对A,由二次函数图象可知,a<0,-<0,所以b<0,函数y=xa+b不符合要求,同理B不符合要求;对于C,D,由二次函数图象可知,a<0,->0,所以b>0,比较选项C,D可知C符合要求.
3.(2015·山西晋城二模,5)设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则不等式
<0的解集为( )
A.(-1,0)∪(1,+∞) B.(-∞,-1)∪(0,1)
C.(-∞,-1)∪(1,+∞) D.(-1,0)∪(0,1)
【答案】 D f(x)为奇函数,所以不等式<0化为<0,即xf(x)<0,f(x)的大致图象如图所示.
所以xf(x)<0的解集为(-1,0)∪(0,1).
4.(2015·江西南昌二模,5)现有四个函数:①y=xsin x,②y=xcos x,③y=x|cos x|,④y=x·2x的图象(部分)如下,但顺序被打乱,则按照从左到右将图象对应的函数序号安排正确的一组是( )
A.④①②③ B.①④③②
C.③④②① D.①④②③
【答案】 D 由于函数y=xsin x是偶函数,由图象知,函数①对应第一个图象;函数y=xcos x为奇函数,且当x=π时,y=-π<0,故函数②对应第三个图象;函数y=x|cos x|为奇函数,故函数③与第四个图象对应;函数y=x·2x为非奇非偶函数,与第二个图象对应.综上可知,选D.
5.(2015·陕西汉中模拟,6)已知函数y=f(x)的大致图象如图所示,则函数y=f(x)的解析式应为( )
A.f(x)=exlnx B.f(x)=e-xln|x|
C.f(x)=exln|x| D.f(x)=e|x|ln|x|
【答案】 C 由题图知,函数的定义域是{x|x≠0,x∈R},排除选项A;当x→-∞时,f(x)→0,
排除选项B,D.因此选C.
6.(2015·湖北武汉三模,7)对实数a和b,定义运算“□”:a□b=设函数f(x)=(x2-2)□(x-1),x∈R.若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
A.(-1,1]∪(2,+∞) B.(-2,-1]∪(1,2]
C.(-∞,-2)∪(1,2] D.[-2,-1]
【答案】 B 令(x2-2)-(x-1)≤1,得-1≤x≤2,
∴f(x)=若函数y=f(x)-c的图象与x轴恰有两个公共点,画出函数f(x)的图象知,实数c的取值范围是(-2,-1]∪(1,2].
7.(2015·河南洛阳模拟,9)已知函数f(x)=若a,b,c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围是( )
A.(1,2 015) B.(1,2 016)
C.[2,2 016] D.(2,2 016)
【答案】 D 作出函数的图象,直线y=m交函数图象如图,不妨设a1时,如图(1).
由图象可知,存在实数b,使g(x)=f(x)-b有两个零点.
当a<0时,如图(2).
由图象可知,存在实数b,使g(x)=f(x)-b有两个零点.
当0≤a≤1时,如图(3).
由图象可知,g(x)=f(x)-b最多有一个零点.
综上可得a的取值范围为(-∞,0)∪(1,+∞).
【答案】 (-∞,0)∪(1,+∞)
4.(2015·江苏,13,难)已知函数f(x)=|ln x|,g(x)=则方程|f(x)+g(x)|=1实根的个数为________.
【解析】 ∵|f(x)+g(x)|=1,
∴g(x)=-f(x)+1或g(x)=-f(x)-1,
①当g(x)=-f(x)+1时,
由图可知,此时y=g(x)与y=-f(x)+1的图象有两个交点,
即g(x)=-f(x)+1有2个实根.
②当g(x)=-f(x)-1时,
由图可知,此时y=g(x)与y=-f(x)-1的图象有两个交点.
即g(x)=-f(x)-1有2个实数.
综合①②,可知方程有4个实根.
【答案】 4
5.(2015·北京,14,难)设函数f(x)=
(1)若a=1,则f(x)的最小值为________;
(2)若f(x)恰有2个零点,则实数a的取值范围是________.
【解析】 (1)若a=1,
则f(x)=
当x<1时,f(x)=2x-1,
f(x)无最小值;
当x≥1时,f(x)=4(x-1)(x-2)=4-1,
∴当x=时,f(x)取得最小值,
即f(x)min=f=-1.
∴f(x)的最小值为-1.
(2)①若f(x)在x<1时恰有1个零点,则∴00,sin x>0,
∴f′(x)>0,故f(x)在[0,1]上单调递增,且f(0)=-1<0,f(1)=1-cos 1>0,所以f(x)在[0,1]内有唯一零点.当x>1时,f(x)=-cos x>0,故函数f(x)在[0,+∞)上有且仅有一个零点,故选B.
3.(2012·辽宁,11,中)设函数f(x)(x∈R)满足f(-x)=f(x),f(x)=f(2-x),且当x∈[0,1]时,f(x)=x3.又函数g(x)=|xcos(πx)|,则函数h(x)=g(x)-f(x)在上的零点个数为( )
A.5 B.6 C.7 D.8
【答案】 B ∵f(-x)=f(x),f(x)=f(2-x),
∴f(-x)=f(2-x),∴f(x)的周期为2.如图画出f(x)与g(x)的图象,它们共有6个交点,故h(x)在上的零点个数为6.故选B.
4.(2011·山东,10,中)已知f(x)是R上最小正周期为2的周期函数,且当0≤x<2时,f(x)=x3-x,则函数y=f(x)的图象在区间[0,6]上与x轴的交点的个数为( )
A.6 B.7 C.8 D.9
【答案】 B 当0≤x<2时,令f(x)=x3-x=0,得x=0或x=1或x=-1(舍去).又f(x)的最小正周期为2,∴f(0)=f(2)=f(4)=f(6)=0,f(1)=f(3)=f(5)=0,∴y=f(x)的图象在区间[0,6]上与x轴的交点个数为7,故选B.
5.(2014·天津,14,难)已知函数f(x)=|x2+3x|,x∈R.若方程f(x)-a|x-1|=0恰有4个互异的实数根,则实数a的取值范围为________.
【解析】 在同一坐标系中,分别作出y1=|x2+3x|,y2=a|x-1|的图象,将方程根的个数问题转化为两图象交点的个数问题求解.
设y1=f(x)=|x2+3x|,y2=a|x-1|,
在同一直角坐标系中作出y1=|x2+3x|,y2=a|x-1|的图象如图所示.
由图可知f(x)-a|x-1|=0有4个互异的实数根等价于y1=|x2+3x|与y2=a|x-1|的图象有4个不同的交点,且4个交点的横坐标都小于1,
所以有两组不同解.
消去y得x2+(3-a)x+a=0有两个不等实根,
所以Δ=(3-a)2-4a>0,
即a2-10a+9>0,
解得a<1或a>9.
又由图象得a>0,∴09.
【答案】 (0,1)∪(9,+∞)
6.(2011·山东,16,难)已知函数f(x)=logax+x-b(a>0,且a≠1).当2<a<3<b<4时,函数f(x)的零点x0∈(n,n+1),n∈N*,则n=________.
【解析】 方法一:∵2<a<3,∴f(x)=logax+x-b为定义域上的增函数,f(2)=loga2+2-b,f(3)=loga3+3-b.
∵2<a,lg 2<lg a,∴loga2=<1.
又∵b>3,
∴-b<-3,∴2-b<-1,∴loga2+2-b<0,
即f(2)<0.∵a<3,∴lg a<lg 3,
∴1<=loga3.
又∵3<b<4,∴-1<3-b<0,∴loga3+3-b>0,∴f(3)>0,即f(2)·f(3)<0.
由x0∈(n,n+1),n∈N*,可知n=2.
方法二:(数形结合法)由f(x)=0,得logax+x-b=0,logax=-x+b.
令g(x)=logax,φ(x)=-x+b.
在同一坐标系下画出g(x),φ(x)的图象,由图象可以看出两图象交点的横坐标x0∈(2,3),∴n=2.
【答案】 2
考向1 函数零点的判断与求解
1.函数零点的等价关系
2.零点存在性定理
——
零点存在性定理只能判断函数在某区间上是否存在零点,并不能判断零点的个数,但如果函数在区间上是单调函数,则该函数在区间上至多有一个零点.
(1)(2013·重庆,6)若a0,f(b)<0,f(c)>0,又该函数是二次函数,且图象开口向上,可知两个零点分别在(a,b)和(b,c)内.
(2)方法一:f(x)=2x|log0.5x|-1
=
=
∵f(x)=-2xlog2x-1在(0,1]上递减且x接近于0时,f(x)接近于正无穷大,f(1)=-1<0,∴f(x)在(0,1]上有1个零点.
又∵f(x)=2xlog2x-1在(1,+∞)上递增,且f(2)=22×log22-1=3>0,
∴f(x)在(1,+∞)上有1个零点,
故f(x)共有2个零点.
方法二:易知函数f(x)=2x|log0.5x|-1的零点个数⇔方程|log0.5x|==的根的个数⇔函数y1=|log0.5x|与y2=的图象的交点个数.作出两个函数的图象如图所示,由图可知两个函数图象有2个交点.
【答案】 (1)A (2)B
【点拨】 解题(1)的依据是零点存在性定理;解题(2)方法一的依据是零点存在性定理,方法二的关键是将零点个数问题转化为两个函数图象的交点个数问题,数形结合求解.
1.判断函数在某个区间上是否存在零点的方法
(1)解方程:当函数对应的方程易求解时,可通过解方程判断方程是否有根落在给定区间上;
(2)利用零点存在性定理进行判断;
(3)画出函数图象,通过观察图象与x轴在给定区间上是否有交点来判断.
2.判断函数零点个数的方法
(1)直接法:解方程f(x)=0,方程有几个解,函数f(x)就有几个零点;
(2)图象法:画出函数f(x)的图象,函数f(x)的图象与x轴的交点个数即为函数f(x)的零点个数;
(3)将函数f(x)拆成两个常见函数h(x)和g(x)的差,从而f(x)=0⇔h(x)-g(x)=0⇔h(x)=g(x),则函数f(x)的零点个数即为函数y=h(x)与函数y=g(x)的图象的交点个数;
(4)二次函数的零点问题,通过相应的二次方程的判别式Δ来判断.
(1)(2015·山东威海一模,4)函数f(x)=x3-的零点所在的区间为( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
(2)(2015·安徽黄山质检,8)若定义在R上的偶函数f(x)满足f(x+2)=f(x),且当x∈[0,1]时,f(x)=x,则方程f(x)=log3|x|的解的个数是( )
A.0 B.2 C.4 D.6
(1)【答案】 B ∵f(1)=-1<0,f(2)=7>0,
∴f(1)·f(2)<0.又函数f(x)在定义域上单调递增,∴由零点存在性定理得f(x)的零点所在区间为(1,2).
(2)【答案】 C 画出周期函数f(x)和y=log3|x|的图象,如图所示,由图知方程f(x)=log3|x|的解的个数为4.
考向2 函数零点的应用
二次函数y=ax2+bx+c(a>0)零点的分布
根的分布(m0,所以f(x)>0,故函数f(x)在(1,2)上没有零点.f(2)=1-ln 1=1,f(3)=-ln 2==.∵=2≈2.828>e,
∴8>e2,即ln 8>2,即f(3)<0.又f(4)=-ln 3<0,∴f(x)在(2,3)内存在一个零点.
3.(2015·山东临沂一模,6)若函数f(x)=(m-2)x2+mx+(2m+1)的两个零点分别在区间(-1,0)和区间(1,2)内,则m的取值范围是( )
A. B.
C. D.
【答案】 C 依题意,结合函数f(x)的图象分析可知m需满足
即
解得0时,有3个零点;当k<0时,有2个零点
B.当k>0时,有4个零点;当k<0时,有1个零点
C.无论k为何值,均有2个零点
D.无论k为何值,均有4个零点
【答案】 B 当k>0时,令f(f(x))=-1,结合图(1)分析,则f(x)=t1∈或f(x)=t2∈(0,1).对于f(x)=t1,存在两个零点x1,x2;对于f(x)=t2,存在两个零点x3,x4.此时存在4个零点;当k<0时,令f(f(x))=-1,结合图(2)分析,则f(x)=t∈(0,1),此时仅有1个零点x0.
6.(2015·云南昆明模拟,14)已知函数f(x)=ax+x-b的零点x0∈(n,n+1)(n∈Z),其中常数a,b满足2a=3,3b=2,则n=________.
【解析】 a=log23>1,b=log32<1,令f(x)=0,得ax=-x+b.在同一平面直角坐标系中画出函数y=ax和y=-x+b的图象,如图所示,
由图可知,两函数的图象在区间(-1,0)内有交点,所以函数f(x)在区间(-1,0)内有零点,所以n=-1.
【答案】 -1
7.(2015·河北唐山模拟,15)已知f(x)=且函数y=f(x)+ax恰有3个不同的零点
,则实数a的取值范围是________.
【解析】 当x<0时,f(x)=(x+1)2-,把函数f(x)在[-1,0)上的图象向右平移一个单位,即得函数y=f(x)在[0,1)上的图象,继续右移可得函数f(x)在[0,+∞)上的图象.如果函数y=f(x)+ax恰有3个不同的零点,即函数y=f(x),y=-ax的图象有三个不同的公共点,实数a应满足-a<-,即a>.
【答案】
8.(2014·江西南昌质检,13)已知函数f(x)=x+2x,g(x)=x+ln x,h(x)=x--1的零点分别为x1,x2,x3,则x1,x2,x3的大小关系是________.
【解析】 令x+2x=0,得2x=-x;
令x+ln x=0,得ln x=-x;
在同一坐标系内画出y=2x,y=ln x,y=-x的图象.如图可知x1<0<x2<1.
令h(x)=x--1=0,
则()2--1=0,
所以=,即x3=>1.
所以x1<x2<x3.
【答案】 x1<x2<x3
思路点拨:解题关键是构造函数画出y=2x,y=ln x,y=-x的图象,观察图象,可得x1,x2的大小关系.
(2015·江苏,17,14分,中)某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路和山区边界的直线型公路.记两条相互垂直的公路为l1,l2,山区边界曲线为C,计划修建的公路为l.如图所示,M,N为C的两个端点,测得点M到l1,l2的距离分别为5千米和40千米,点N到l1,l2的距离分别为20千米和2.5千米,以l2,l1所在的直线分别为x,y轴,建立平面直角坐标系xOy.假设曲线C符合函数y=(其中a,b为常数)模型.
(1)求a,b的值;
(2)设公路l与曲线C相切于P点,P的横坐标为t.
①请写出公路l长度的函数解析式f(t),并写出其定义域;
②当t为何值时,公路l的长度最短?求出最短长度.
解:(1)由题意知,点M,N的坐标分别为(5,40),(20,2.5).
将其分别代入y=,
得解得
(2)①由(1)知,y=(5≤x≤20),则点P的坐标为,
设在点P处的切线l交x,y轴分别于A,B点,y′=-,
则l的方程为y-=-(x-t),由此得A,B.
故f(t)=
=,t∈[5,20].
②设g(t)=t2+,则g′(t)=2t-.令g′(t)=0,解得t=10.
当t∈(5,10)时,g′(t)<0,g(t)是减函数;
当t∈(10,20)时,g′(t)>0,g(t)是增函数.
从而,当t=10时,函数g(t)有极小值,也是最小值,所以g(t)min=300,
此时f(t)min=15.
1.(2014·湖南,8,易)某市生产总值连续两年持续增加.第一年的增长率为p,第二年的增长率为q,则该市这两年生产总值的年平均增长率为( )
A. B.
C. D.-1
【答案】 D 设这两年的平均增长率为m,
则有(1+p)(1+q)=(1+m)2,
∴m=-1.
2.(2011·北京,6,易)根据统计,一名工人组装第x件某产品所用的时间(单位:分钟)为f(x)=(A,c为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是( )
A.75,25 B.75,16 C.60,25 D.60,16
【答案】 D 由条件可知,x≥A时所用时间为常数,所以组装第4件产品用时必然满足第一个分段函数,即=30,解得c=60.组装第A件产品用时15分钟,则=15,A=16,故选D.
3.(2011·江苏,17,14分,中)请你设计一个包装盒.如图所示,ABCD是边长为60 cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒.E,F在AB上,是被切去一个等腰直角三角形斜边的两个端点.设AE=FB=x(cm).
(1)某广告商要求包装盒的侧面积S(cm2)最大,试问x应取何值?
(2)某厂商要求包装盒的容积V(cm3)最大,试问x应取何值?并求出此包装盒的高与底面边长的比值.
解:设包装盒的高为h cm,底面边长为a cm.
由已知得a=x,
h==(30-x),00;当x∈(20,30)时,V′<0.所以当x=20时,V取得极大值,也是最大值.
此时a=20,h=10,=,
即包装盒的高与底面的边长的比值为.
4.(2011·湖南,20,13分,中)如图,长方体物体E在雨中沿面P(面积为S)的垂直方向做匀速移动,速度为v(v>0),雨速沿E移动方向的分速度为c(c∈R).E移动时单位时间内的淋雨量包括两部分:①P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与|v-c|×S成正比,比例系数为;②
其他面的淋雨量之和,其值为.记y为E移动过程中的总淋雨量.当移动距离d=100,面积S=时,
(1)写出y的表达式;
(2)设01)
y=logax(a>1)
y=xn(n>0)
在(0,+∞)上的单调性
单调增函数
单调增函数
单调增函数
增长速度
越来越快
越来越慢
相对平稳
图象的变化
随x的增大逐渐表现为与y轴平行
随x的增大逐渐表现为与x轴平行
随n值变化而各有不同
联系
存在一个x0,当x>x0时,有logax0时,+(m+1)≥2=8,
∴y≤-8+29=21,
当且仅当=m+1,即m=3时,y取得最大值.
∴当该厂家2014年的促销费用投入3万元时,厂家获得的利润最大,为21万元.
(时间:90分钟__分数:120分)
一、选择题(共10小题,每小题5分,共50分)
1.(2015·福建五校联考,7)函数y=log2(|x|+1)的图象大致是( )
【答案】 B 由题意知函数y=log2(|x|+1)的定义域为R,且为偶函数,当x>0时,y=log2(x+1).故选B.
2.(2015·河南新乡二模,5)函数f(x)=-|x-5|+2x-1的零点所在的区间是( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
【答案】 C 依题意得f(0)=-5+<0,f(1)=-4+1<0,f(2)=-3+2<0,f(3)=-2+4>0,f(4)=-1+8>0,∴f(0)·f(1)>0,f(1)·f(2)>0,f(2)·f(3)<0,f(3)·f(4)>0,故f(x)的零点所在区间是(2,3),故选C.
3.(2015·江西九江模拟,6)设甲、乙两地的距离为a(a>0),小王骑自行车以匀速从甲地到乙地用了20分钟,在乙地休息10分钟后,他又以匀速从乙地返回到甲地用了30分钟,则小王从出发到返回原地所经过的路程y和其所用的时间x的函数图象为( )
【答案】 D y为“小王从出发到返回原地所经过的路程”而不是位移,故排除A,C;又因为小王在乙地休息10分钟,故排除B,故选D.
4.(2015·山东济南质检,7)设函数f(x)=2x,则如图所示的图象对应的函数是( )
A.y=f(|x|) B.y=-|f(x)|
C.y=-f(-|x|) D.y=f(-|x|)
【答案】 C 该图象是函数y=-2-|x|,
即y=-f(-|x|)的图象.故选C.
5.(2015·山东枣庄一模,7)已知符号函数sgn(x)=则函数f(x)=sgn(ln x)-ln x的零点个数为( )
A.1 B.2
C.3 D.4
【答案】 C 依题意得f(x)=sgn(ln x)-ln x=
令f(x)=0得x=e,1,,所以函数有3个零点.故选C.
6.(2015·湖北宜昌模拟,5)某地2014年底人口为500万,人均住房面积为6 m2,如果该城市人口平均每年增长率为1%,为使2024年底该城市人均住房面积增加到7 m2,平均每年新增住房面积至少为(1.0110≈1.104 6)( )
A.90万m2 B.87万m2
C.85万m2 D.80万m2
【答案】 B 由题意得≈86.61(万m2)≈87(万m2).
方法点拨:指数函数型多涉及增长率、减少率、银行利率、细胞分裂等一系列问题,通常可以表示为y=a(1+p)x的形式,利用指数运算与对数函数求解.
7.(2012·山东,10)函数y=的图象大致为( )
【答案】 D 函数y=cos 6x为偶函数,函数y=2x-2-x为奇函数,故原函数为奇函数,排除A;又函数y=2x-2-x为增函数,当x趋近于+∞时,2x-2-x趋近于+∞且|cos 6x|≤1,∴y=趋近于0(x趋近于+∞),排除C;∵y==为奇函数,不妨考虑x>0时函数值的情况,当x
趋近于0时,4x趋近于1,4x-1趋近于0,2x趋近于1,cos 6x趋近于1,∴y趋近于+∞,故排除B.综上可知选D.
8.(2015·河北石家庄高三模拟,8)[x]表示不超过x的最大整数,例如[2.9]=2,[-4.1]=-5,已知f(x)=x-[x](x∈R),g(x)=log4(x-1),则函数h(x)=f(x)-g(x)的零点个数是( )
A.1 B.2
C.3 D.4
【答案】 B 作出函数f(x)与g(x)的图象如图所示,发现有2个不同的交点,故函数h(x)=f(x)-g(x)的零点个数为2.
9.(2015·湖北宜昌模拟,7)某种新药服用x小时后血液中的残留量为y毫克,如图所示为函数y=f(x)的图象,当血液中药物残留量不小于240毫克时,治疗有效.设某人上午8:00第一次服药,为保证疗效,则第二次服药最迟的时间应为( )
A.上午10:00 B.中午12:00
C.下午4:00 D.下午6:00
【答案】 C 当x∈[0,4]时,设y=k1x,把(4,320)代入,得k1=80,∴y=80x.
当x∈[4,20]时,设y=k2x+b.
把(4,320),(20,0)代入得
解得 ∴y=400-20x.
∴y=f(x)=
由y≥240,
得或
解得3≤x≤4或40.
∵a>0,f(x)=a[(x-1)2-4]≥-4且f(1)=-4a,
∴f(x)min=-4a=-4,
∴a=1.故函数f(x)的解析式为f(x)=x2-2x-3.
(2)∵g(x)=-4ln x
=x--4ln x-2(x>0),
g′(x)=1+-
=,
∴x,g′(x),g(x)的取值变化情况如下:
x
(0,1)
1
(1,3)
3
(3,+∞)
g′(x)
+
0
-
0
+
g(x)
单调递增
极大值
单调递减
极小值
单调递增
当03,
g(e5)=e5--20-2>25-1-22=9>0.
故函数g(x)只有1个零点,且零点x0∈(3,e5).