中考数学模拟分类汇编-开放探究型问题
开放探究型问题
一、填空题
1、(年北京四中模拟 28)
两个不相等.....的无理数,它们的乘积为有理数,这两个数可以是.
答案:略
二、解答题
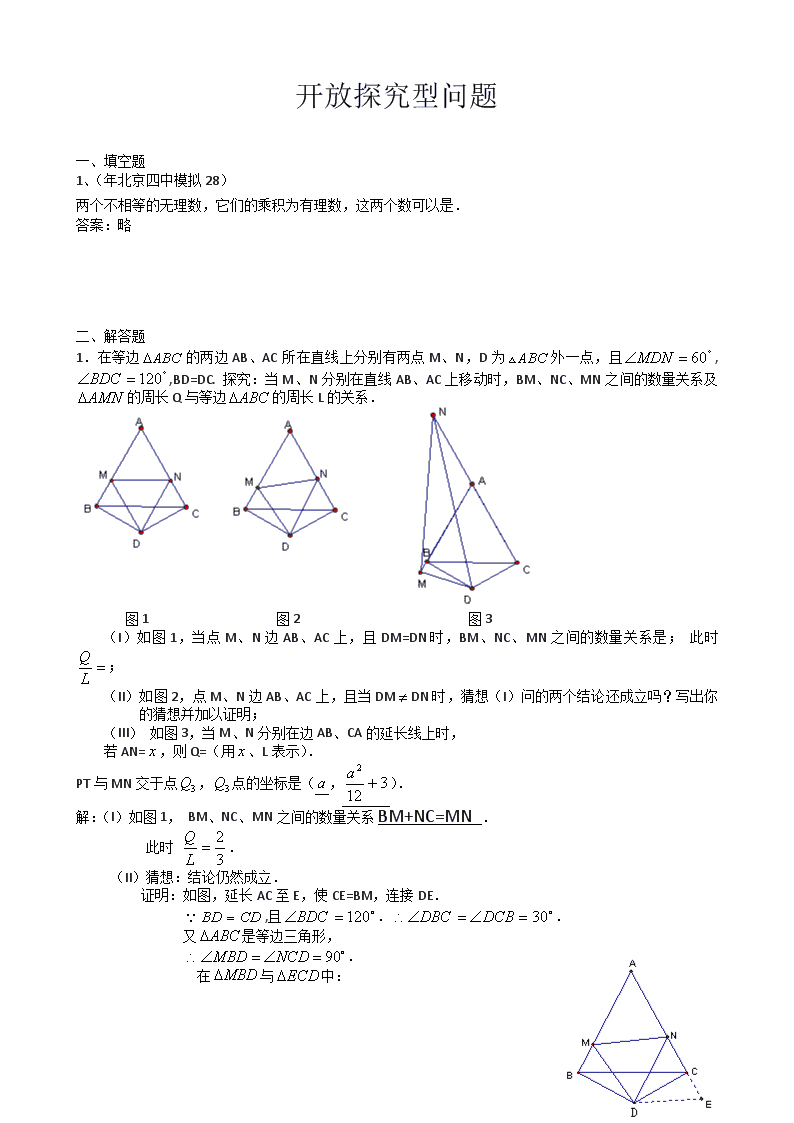
1 . 在 等 边 ABC 的 两 边 AB 、 AC 所 在 直 线 上 分 别 有 两 点 M 、 N , D 为 ABC 外 一 点 , 且
60MDN , 120BDC ,BD=DC. 探究:当 M、N 分别在直线 AB、AC 上移动时,BM、NC、MN 之间
的数量关系及 AMN 的周长 Q 与等边 ABC 的周长 L 的关系.
图 1 图 2 图 3
(I)如图 1,当点 M、N 边 AB、AC 上,且 DM=DN 时,BM、NC、MN 之间的数量关系是; 此时
L
Q ;
(II)如图 2,点 M、N 边 AB、AC 上,且当 DM DN 时,猜想(I)问的两个结论还成立吗?写出你
的猜想并加以证明;
(III) 如图 3,当 M、N 分别在边 AB、CA 的延长线上时,
若 AN= x ,则 Q=(用 x 、L 表示).
PT 与 MN 交于点 3Q , 3Q 点的坐标是( a , 312
2
a ).
解:(I)如图 1, BM、NC、MN 之间的数量关系 BM+NC=MN .
此时
3
2
L
Q .
(II)猜想:结论仍然成立.
证明:如图,延长 AC 至 E,使 CE=BM,连接 DE.
CDBD ,且 120BDC . 30 DCBDBC .
又 ABC 是等边三角形,
90MBD NCD .
在 MBD 与 ECD 中:
DCBD
ECDMBD
CEBM
y
O
M
xn
l
1 2 3
…
1B
2B
3B
nB
1A 2A 3A 4A nA 1nA
MBD ECD (SAS) .
DM=DE, CDEBDM
60 MDNBDCEDN
在 MDN 与 EDN 中:
DNDN
EDNMDN
DEDM
MDN EDN (SAS)
MN=NE=NC+BM
AMN 的周长 Q=AM+AN+MN
=AM+AN+(NC+BM)
=(AM+BM)+(AN+NC)
=AB+AC
=2AB
而等边 ABC 的周长 L=3AB
3
2
3
2
AB
AB
L
Q .
(III)如图 3,当 M、N 分别在 AB、CA 的延长线上时,若 AN= x ,
则 Q=2 x + L3
2 (用 x 、L 表示).
B组
解答题
1.( 天一实验学校 二模)已知:如图,直线 l : 1
3y x b ,经过点 M(0,
4
1 ),一组抛物线的顶点
1 1 2 2 3 3(1 ) (2 ) (3 ) ( )n nB y B y B y B n y, , , , , , , , ( n 为正整数)依次是直线l 上的点,这组抛物线与 x
轴正半轴的交点依次是:A1(x1,0), A2(x2,0), A3(x3,0),……An+1(xn+1,0)( n 为正整数),设 1 0 1x d d ( ).
(1)求 b 的值;
(2)求经过点 1 1 2A B A、 、 的抛物线的解析式(用含 d 的代数式表示)
(3)定义:若抛物线的顶点与 x 轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为:“美
丽抛物线”.
探究:当 0 1d d ( )的大小变化时,这组抛物线中是否存在美丽抛物线?若存在,请你求出相应的 d
的值.
答案:
⑴∵M(0, )4
1 在直线 y=
3
1 x+b 上,
∴b=
4
1
⑵由⑴得 y=
3
1 x+
4
1 ,∵B1(1,y1)在直线 l 上, ∴当 x=1 时,y1=
3
1 ×1+
4
1 =
12
7
∴B1(1,
12
7 )
又∵A1(d,0) A2(2-d,0)
设 y=a(x-d)(x-2+d),把 B1(1,
12
7 )代入得:a=- 2)1(12
7
d
∴过 A1、B1、A2 三点的抛物线解析式为 y=- 2)1(12
7
d
(x-d)(x-2+d)
(或写出顶点式为 y=- 2)1(12
7
d
(x-1) 2 +
12
7 )
⑶存在美丽抛物线。
由抛物线的对称性可知,所构成的直角三角形必定是以抛物线为顶点为直角顶点的等腰直角三角形,此等
腰直角三角形斜边上的高等于斜边的一半,又∵0
1
∴美丽抛物线的顶点只有 B1B2.
①若 B1 为顶点,由 B1(1,
12
7 ),则 d=1-
12
7 =
12
5
②若 B2 为顶点,由 B2(2,
12
11 ),则 d=1-
1)12
112( =
12
11
综上所述,d 的值为
12
5 或
12
11 时,存在美丽抛物线。
2.(年杭州市西湖区模拟)(本题 12 分)矩形OABC 在直角坐标系中的位置如图所示, A 、C 两点的坐
标分别为 (6,0)A 、 (0,3)C ,直线 3
4y x 与 BC 边相交于点 D .
(1) 若抛物线 2 ( 0)y ax bx a 经过 D 、 A 两点,试确定此抛物线的表达式;
(2) 若以点 A 为圆心的⊙ A 与直线OD 相切,试求⊙ A 的半径;
(3) 设(1)中抛物线的对称轴与直线 OD 交于点 M ,在对称轴上是否存在点Q ,以Q 、O 、 M 为顶
点的三角形与 OCD 相似,若存在,试求出符合条件的Q 点的坐标;若不存在,试说明理由.
答案:(1)解
xy
y
4
3
3
得 D 点的坐标为 D(4,3)
抛物线 bxaxy 2 经过 D(4,3)、A(6,0),可得
xxy 4
9
8
3 2
第 2 题
(2)∵CD=4,OC=3,OD= 534 32 . sin∠CDO=
5
3 ,过 A 作 AH⊥OD 于 H,
则 AH=OAsin∠DOA=6×
5
3 =
5
18 =3.6, ∴当直线 OD 与⊙A 相切时,r=3.6.………8 分
(3)设抛物线的对称轴与 x 轴交于点 Q 1 ,则点 Q 1 符合条件.∵CB∥OA,∴∠Q 1 OM=∠ODC,
∴Rt△Q 1 OM ∽Rt△CDO.∵对称轴 x = 32
a
b ,∴Q 1 点的坐标为 Q 1 (3,0).
又过 O 作 OD 的垂线交抛物线的对称轴于点 Q 2 ,则点 Q 2 也符合条件.∵对称轴平行于 y 轴,
∴∠Q 2 MO=∠DOC,∴Rt△Q 2 MO∽Rt△DOC. 在 Rt△Q 2 Q 1 O 和 Rt△DCO 中,Q 1 O=CO=3,
∠Q 2 =∠ODC,∴Rt△Q 2 Q 1 O≌Rt△DCO,∴CD= Q 1 Q 2 =4,∵Q 2 位于第四象限,
∴Q 2 (3,-4).因此,符合条件的点有两个,分别是 Q 1 (3,0),Q 2 (3,-4).
3.(灌南县新集中学一模)如图,已知直角梯形 ABCD 中,AD∥BC,∠ABC=90°,AD=AB=3,BC=4,
动点 P 从 B 点出发,沿线段 BC 向点 C 作匀速运动;动点 Q 从点 D 出发,沿线段 DA 向点 A 作匀速运动.过
Q 点垂直于 AD 的射线交 AC 于点 M,交 BC 于点 N.P、Q 两点同时出发,速度都为每秒 1 个单位长度,当 Q
点运动到 A 点,P、Q 两点同时停止运动.设点 Q 运动的时间为 t 秒.
(1)求 NC、MC 的长(用含 t 的代数式表示);
(2)当 t 为何值时,四边形 PCDQ 构成平行四边形?
(3)是否存在某一时刻 t,使射线 QN 恰好将△ABC 的面积和周长同时平分?若存在,求出此时 t 的值;
若不存在,请说明理由;
(4)探究:t 为何值时,△PMC 为等腰三角形?
答案:.解:(1)由题意知,四边形 ABNQ 为矩形,∴BN=AQ=3-t
∴NC=BC-BN=4-(3-t)=1+t.
在 Rt△ABC 中,AC2=AB2+BC2=32+42=25,∴AC=5
在 Rt△MNC 中,cos∠MCN=
MC
NC =
AC
BC =
5
4 ∴MC=
4
5 (1+t)
(2)∵QD∥PC,∴当 QD=PC 时,四边形 PCDQ 构成平行四边形
∴t=4-t,∴t=2 ∴当 t=2 时,四边形 PCDQ 构成平行四边形.
(3)若射线 QN 将△ABC 的周长平分,则有 MC+NC=AM+BN+AB
即
4
5 (1+t)+1+t=
2
1 (3+4+5) 解得 t=
3
5 .而 MN=
4
3 NC=
4
3 (1+t)
A
B C
DQ
M
NP
∴S△MNC =
2
1 NC·MN=
2
1 (1+t)×
4
3 (1+t)=
8
3 (1+t)2
当 t=
3
5 时,S△MNC =
8
3 (1+
3
5 )2
=
3
8
而
2
1 S△ABC =
2
1 ×
2
1 ×4×3=3,∴S△MNC ≠
2
1 S△ABC
∴不存在某一时刻 t,使射线 QN 恰好将△ABC 的面积和周长同时平分
(4)若△PMC 为等腰三角形,则:
①当 MP=MC 时(如图 1),则有:NP=NC
即 PC=2NC,∴4-t=2(1+t) 解得 t=
3
2 .
当 CM=CP 时(如图 2),则有:
4
5 (1+t)=4-t 解得 t=
9
11 .
③当 PM=PC 时(如图 3),则有:
在 Rt△MNP 中,PM2=MN2+PN2 又 MN=
4
3 NC=
4
3 (1+t)
PN=NC-PC=(1+t)-(4-t)=2t-3
∴[
4
3 (1+t)]2+(2t-3)2=(4-t)2 解得 t1=
57
103 ,t2=-1(不合题意,舍去)
综上所述,当 t=
3
2 或 t=
9
11 或 t=
57
103 时,△PMC 为等腰三角形.
4. (浙江杭州育才初中模拟)《天天伴我学数学》一道作业题。如图 1:请你想办法求出五角星中
A B C D E 的值。由于刚涉及到几何证明,很多学生不知道如何求出其结果。下面是
习题讲解时,老师和学生对话的情景:老师向学生抛出问题:①观察图像,各个角的度数能分别求出他
们的度数吗,能的话怎么求,不能的话怎么办?学生通过观察回答:很明显每个角都不规则,求不出各
个角的度数。有个学生小声的说了句:要是能把这五个角放到一块就好了?老师回答:有想法,就去试
试看。很快就有学生发现利用三角形外角性质将∠C 和∠E;∠B 和∠D 分别用外角∠1 和∠2 表示。于是
得到 A B C D E = 1 2A 180°。根据以上信息,亲爱的同学们,你能求出图
2 中 A B C D E F G 的值吗?请给予证明。(原创)
A
B C
DQ
M
NP
图 1
A
B C
DQ
M
NP
图 2
A
B C
DQ
M
N P
图 3
�
A
�
C
�
E
�
B
�
D
�
图1
�
G
�
F
�
2
�
1
�
D
�
Q
�
B
�
C
�
E
�
A
�
图 �2
�
G
�
F
5、(北京四中中考模拟 13)已知:如图,⊙O 1 和⊙O 2 相交于 A、B 两点,动点 P 在⊙O 2 上,且在⊙ 1 外,
直线 PA、PB 分别交⊙O 1 于 C、D.问:⊙O 1 的弦 CD 的长是否随点 P 的运动而发生变化?如果发生变化,请
你确定 CD 最长和最短时 P 的位置,如果不发生变化,请你给出证明;
答案:解:当点 P 运动时,CD 的长保持不变,A、B 是⊙O 1 与 ⊙ O 2 的 交
点,弦 AB 与点 P 的位置关系无关,连结 AD,∠ADP 在⊙O 1 中 所对的弦为
AB,所以∠ADP 为定值,∠P 在⊙O 2 中所对的弦为 AB,所以 ∠P 为定值.
∵∠CAD =∠ADP +∠P,∴∠CAD 为定值,
在⊙O 1 中∠CAD 对弦 CD,∴CD 的长与点 P 的位置无关.
6、(北京四中中考模拟 14)
探究题:将一把三角尺放在边长为 1 的正方形 ABCD 上,并使它的直角顶点 P 在对角线 AC 上滑动,直角的
一边始终经过点 B,另一边与射线 DC 相交于点 Q。设 A、P 两点间的距离为 X,探究:
(1)当点 Q 在边 CD 上时,线段 PQ 与线段 PB 之间有怎样的大小关系?试证明你得到的结论。
(2)当点 Q 在边 CD 上时,设四边形 PBCQ 的面积为 y,求 y 与 x 之间的函数解析式,并写出函数自变量的
取值范围;
(3)当点 P 在线段 AC 上滑动时,△PCQ 是否可能成为等腰三角形?如果可能,指出所有能使△PCQ 成为
等腰三角形的点 Q 的位置,并求出响应的 X 的值;如果不可能,请说明理由。
答案:(1):过点 P 作 MN∥BC,分别交 AB 与点 M,交 CD 于 N,则有△AMP 和△CNP 都是等腰三角形,可证△QNP
≌△PMB,得 PQ=PB.
(2)图(2)由 AP=x 得 AM=PM=NQ=
2
2 x,CQ=CN-NQ=BM-AM=1- 2 x,
y=
2
1 (BC+CQ)=
2
1 x2- 2 x+1(0≤x<
2
2 )
(3)三角形 PCQ 为等腰三角形.
①点 P 与点 A 重合时,点 Q 与点 D 重合,这时 PQ=QC, 三角形 PCQ 为等腰三角形.
②点 Q 在 DC 的延长线上时且 CP=CQ 时,三角形 PCQ 为等腰三角形。求得 x=1.
�
O
�
2
�
A
�
B
�
O
�
1
�
P
�
D
�
C
7、(年黄冈浠水模拟 1)如图 1,已知抛物线的顶点为 (21)A , ,且经过原点O ,与 x 轴的另一个交点为 B .
(1)求抛物线的解析式;
(2)若点 C 在抛物线的对称轴上,点 D 在抛物线上,且以 O C D B, , , 四点为顶点的四边形为平行四
边形,求 D 点的坐标;
(3)连接OA AB, ,如图 2,在 x 轴下方的抛物线上是否存在点 P ,使得 OBP△ 与 OAB△ 相似?若存
在,求出 P 点的坐标;若不存在,说明理由.
答案:(1)由题意可设抛物线的解析式为 2( 2) 1y a x .抛物线过原点,
20 (0 2) 1a . 1
4a .抛物线的解析式为 21 ( 2) 14y x ,
即 21
4y x x .
(2)如图 1,当四边形OCDB 是平行四边形时,
CD OB�∥ .
由 21 ( 2) 1 04 x ,得 1 0x , 2 4x , (4 0)B , , 4OB .
D 点的横坐标为 6 .将 6x 代入 21 ( 2) 14y x ,
得 21 (6 2) 1 34y , (6 3)D , ;
根据抛物线的对称性可知,在对称轴的左侧抛物线上存在点 D ,使得四边形ODCB 是平行四边形,此时 D
点的坐标为 ( 2 3) , .
当四边形 OCBD 是平行四边形时, D 点即为 A 点,此时 D 点的坐标为 (21), .····· (8 分)
(3)如图 2,由抛物线的对称性可知:
AO AB , AOB ABO∠ ∠ .
若 BOP△ 与 AOB△ 相似,
必须有 POB BOA BPO ∠ ∠ ∠ .
设OP 交抛物线的对称轴于 A点,
显然 (2 1)A , ,直线OP 的解析式为 1
2y x .
由 21 1
2 4x x x ,得 1 0x , 2 6x . (6 3)P , .过 P 作 PE x 轴,
在 Rt BEP△ 中, 2BE , 3PE , 2 22 3 13 4PB .
PB OB . BOP BPO ∠ ∠ .
PBO△ 与 BAO△ 不相似,同理可说明在对称轴左边的抛物线上也不存在符合条件的 P 点.
所以在该抛物线上不存在点 P ,使得 OBP△ 与 OAB△ 相似.
y
x
A
BO
y
x
A
BO
图 1 图 2
y
x
A
BO
图 1
C D
y
x
A
BO
图 2
E
P
A
8、(年黄冈浠水模拟 2)如图二次函数的图象经过点 D(0, 39
7 ),且顶点 C 的横坐标为 4,该图象在 x 轴
上截得线段 AB 长为 6.
(1)利用二次函数的对称性直接写出点 A、B 的坐标为:A( , )、B( , );
(2)求二次函数的解析式;
(3)该抛物线的对称轴上找一点 P,使 PA+PD 最小,求出点 P 的坐标;
(4)在抛物线上是否存在点 Q,使△QAB 与△ABC 相似?如果存在,求出点 Q 的坐标;如果不存在,请说明
理由.
答案:(1) ∵对称轴为直线 x=4,图象在 x 轴上截得的线段长为 6,∴ A( 1 , 0 )、B( 7 , 0 );
(2)设二次函数的解析式为:y=a(x-h)2+k,∵顶点 C 的横坐标为 4,且过点(0, 39
7 )
∴y=a(x-4)2+k ka 1639
7 ………………①
又∵对称轴为直线 x=4,图象在 x 轴上截得的线段长为 6,∴A(1,0),B(7,0)
∴0=9a+k ………………②,由①②解得 a=
9
3 ,k= 3- ,∴二次函数的解析式为:y=
9
3 (x-4)2- 3 或
y=
9
3 x 2 -
9
316 x+
9
37
………………………………………5 分
(3)解法一:∵点 A、B 关于直线 x=4 对称,∴PA=PB,∴PA+PD=PB+PD≥DB,∴当点 P 在线段 DB 上时 PA+PD
取得最小值,∴DB 与对称轴的交点即为所求点 P,设直线 x=4 与 x 轴交于点 M,∵PM∥OD,∴∠BPM=∠BDO,
又 ∠PBM=∠DBO , ∴△BPM∽△BDO , ∴
BO
BM
DO
PM , ∴
3
3
7
339
7
PM , ∴ 点 P 的 坐 标 为 (4 ,
3
3 )…………………8 分
C
D
O BA
y
x
解法二:利用待定系数法求一次函数解析式,即直线 DB 为 y=- x9
3 +
9
37
(4)由⑴知点 C(4, 3 ),又∵AM=3,∴在 Rt△AMC 中,cot∠ACM=
3
3 ,∴∠ACM=60o,∵AC=BC,∴∠ACB=120o
①当点 Q 在 x 轴上方时,过 Q 作 QN⊥x 轴于 N,如果 AB=BQ,由△ABC∽△ABQ 有 BQ=6,∠ABQ=120o,则∠QBN=60o,
∴QN=3 3 ,BN=3,ON=10,此时点 Q(10, 33 ),如果 AB=AQ,由对称性知 Q(-2, 33 )
②当点 Q 在 x 轴下方时,△QAB 就是△ACB,此时点 Q 的坐标是(4, 3 ),经检验,点(10, 33 )与(-2,
33 )都在抛物线上,综上所述,存在这样的点 Q,使△QAB∽△ABC,点 Q 的坐标为(10, 33 )或(-2, 33 )
或(4, 3 ).…………………………14 分
9、(年杭州模拟 17)在平面直角坐标系中,抛物线经过 O(0,0)、A(4,0)、B(3, 2 3
3
)三点.
(1)求此抛物线的解析式;
(2)以 OA 的中点 M 为圆心,OM 长为半径作⊙M,在(1)中的抛物线上是否存在这样的点 P,过点 P
作⊙M 的切线 l ,且 l 与 x 轴的夹角为 30°,若存在,请求出此时点 P 的坐标;若不存在,请说
明理由.(注意:本题中的结果可保留根号)(2010 昆明中考第 25 题)
答案:(1)设抛物线的解析式为:
2 ( 0)y ax bx c a
由题意得:
0
16 4 0
2 39 3 3
c
a b c
a b c
解得: 2 3 8 3, , 09 9a b c
∴抛物线的解析式为: 22 3 8 3
9 9y x x
(2)存在
(2)抛物线 22 3 8 3
9 9y x x 的顶点坐标是 8 3(2, )9
,作抛物线和⊙M(如图),
设满足条件的切线 l 与 x 轴交于点B,与⊙M相切于点C
连接MC,过C作CD⊥x轴于D
∵MC = OM =2, ∠CBM=30°, CM⊥BC
∴∠BCM=90° ,∠BMC = 60° ,BM=2CM=4 , ∴B (-2, 0)
在Rt△CDM中,∠DCM =∠CDM-∠CMD = 30°
∴DM = 1, CD= 2 2CM DM = 3 ∴C(1, 3 )
设切线l 的解析式为: ( 0)y kx b k= + ¹ ,点B、C在l 上,可得:
3
2 0
k b
k b
解得: 3 2 3,3 3k b
∴切线BC的解析式为: 3 2 3
3 3y x
∵点P为抛物线与切线的交点
由
22 3 8 3
9 9
3 2 3
3 3
y x x
y x
解得:
1
1
1
2
3
2
x
y
2
2
6
8 3
3
x
y
l′
∴点P的坐标为: 1
1 3( , )2 2P , 2
8 3(6, )3P ………………4分
∵ 抛物线 22 3 8 3
9 9y x x 的对称轴是直线 2x
此抛物线、⊙M都与直线 2x 成轴对称图形
于是作切线 l 关于直线 2x 的对称直线 l′(如图)
得到B、C关于直线 2x 的对称点B1、C1
l′满足题中要求,由对称性,得到P1、P2关于直线 2x 的对称点:
3
9 3( , )2 2P , 4
8 3( 2, )3P 即为所求的点. ………………4分
(本题其它解法参照此标准给分)
10.(湖北省崇阳县城关中学模拟) 如图,在第一象限内作射线 OC,与 x 轴的夹角为 30o,在射线 OC 上
取一点 A,过点 A 作 AH⊥x 轴于点 H.在抛物线 y=x2(x>0)上取点 P,在 y 轴上取点 Q,使得以 P,O,
Q 为顶点的三角形与△AOH 全等,则符合条件的点 A 的坐标是.
答案:(
3
3 ,
3
1 )(
3
32 ,
3
2 )(3, 3 )(2 3 ,2)
11.(年广东省澄海实验学校模拟)把两个全等的直角三角板 ABC 和 EFG 叠放在一起,且使三角板 EFG 的
直角顶点 G 与三角板 ABC 的斜边中点 O 重合,其中∠B=∠F=30°,斜边 AB 和 EF 的长均为 4。
(1)当 EG⊥AC 于点 K,GF⊥BC 于点 H 时,如图 23-1,求 GH:GK 的值.
(2)现将三角板 EFG 由图 1 所示的位置绕 O 点沿逆时针方向旋转,旋转 角满足条件:
0°< <30°,如图 2,EG 交 AC 于点 K,GF 交 BC 于点 H,GH:GK 的值是否改变?证明你的结论.
G(O)KE
A
G(O)
K
A
(1)解:∵GE⊥AC 于 K,GF⊥BC 于 H,
∴∠AKG =∠GHB =90°
∵∠ACB =90°
∴GK∥BC……………………………(1 分)
∴∠AGK =∠B =30°………………(2 分)
∵G 与 AB 的中点 O 重合
∴AG = GB
∴△AKG≌△GHB……………………(3 分)
∴KG = HB……………………………(4 分)
在 Rt△GHB 中,tan∠B =
3
3
HB
GH …(5 分)
∴
3
3
GK
GH ……………………………(6 分)
(2)GH:GK 的值不改变。………………………(7 分)
证明:过点 G 作 GP⊥AC 于点 P,GQ⊥BC 于点 Q,
∵∠C = 90°
∴四边形 PCQG 是矩形……………………(8 分)
∴∠PGK+∠KGO = 90°
∵∠EGF = 90°
∴∠HGQ+∠KGQ = 90°
∴∠PGK = ∠HGQ ………………………(9 分)
∵∠GPK =∠GQH = 90°
∴△PGK∽△QGH…………………………(10 分)
∴
GP
GQ
GK
GH 由(1)可得:
3
3
GK
GH …… (11 分)
∴
3
3
GK
GH ………………………………(12 分)
12.(年深圳二模)在△ABC 中,AC=BC,∠ACB=90°,D、E 是直线 AB 上两点.∠DCE=45°
(1)当 CE⊥AB 时,点 D 与点 A 重合,显然 DE 2 =AD 2 +BE 2 (不必证明)
(2)如图,当点 D 不与点 A 重合时,求证:DE 2 =AD 2 +BE 2
(3)当点 D 在 BA 的延长线上时,(2)中的结论是否成立?画出图形,说明理由.
解:(2)证明:
第 2 题图 1
第 2 题图
G(O)K
H
F
E
C B
A
G(O)
E
F
H
K
C B
A
Q
P
第 2 题图 1 第 2 题图 2
�
P
�
N
�
M
�
C
�
B
�
A
�
O
�
y
�
x
过点 A 作 AF ⊥AB ,使 AF=AB,连接 DF
∵△ABC 是等腰直角三角形
∴AC=AB ∠CAB=∠B=45°,
∴∠FAC=45°
∴△CAF≌△CBE…………………………………………3 分
∴CF=CE ∠ACF=∠BCE
∵∠ACB=90°,∠DCE=45°
∴∠ACD+∠BCE=45°
∴∠ACD+∠ACF=45°
即∠DCF=45°
∴∠DCF=∠DCE
又 CD=CD
∴△CDF≌△CDE
∴DF=DE
∵AD 2 +AF 2 =DF 2
∴AD 2 +BE 2 =DE 2 …………………………………………7 分
(3)结论仍然成立
如图证法同(2)…………………………………………12 分
13、(深圳市模四)(深圳市模四)(9 分)如图,在平面直角坐标系中,四边形 OABC 为矩形,点 A、B 的坐
标分别为(6,0),(6,8)。动点 M、N 分别从 O、B 同时出发,以每秒 1 个单位的速度运动。其中,点
M 沿 OA 向终点 A 运动,点 N 沿 BC 向终点 C 运动。过点 N 作 NP⊥BC,交 AC 于 P,连结 MP。已知动点运
动了 x 秒。
(1)P 点的坐标为(,);(用含 x 的代数式表示)
(2)试求 ⊿MPA 面积的最大值,并求此时 x 的值。
(3)请你探索:当 x 为何值时,⊿MPA 是一个等腰三角形?
你发现了几种情况?写出你的研究成果。
解:(1)(6-x ,
3
4 x );
(2)设⊿MPA 的面积为 S,在⊿MPA 中,MA=6﹣x,MA 边上的高为
3
4 x,其中,0≤x≤6.∴S=
2
1 (6—x)×
第 4 题图
第 3 题答案图
3
4 x=
3
2 (﹣x2+6x) = —
3
2 (x﹣3)2+6。∴S 的最大值为 6, 此时 x=3.
(3)延长NP交 x 轴于Q,则有PQ⊥OA
①若MP=PA ∵PQ⊥MA ∴MQ=QA=x. ∴3x=6, ∴x=2;
②若MP=MA,则MQ=6—2x,PQ=
3
4 x,PM=MA=6—x
在Rt⊿PMQ 中,∵PM2=MQ2+PQ2 ∴(6—x) 2=(6—2x) 2+(
3
4 x) 2∴x=
43
108
③若PA=AM,∵PA=
3
5 x,AM=6—x ∴
3
5 x=6—x ∴x=
4
9
综上所述,x=2,或 x=
43
108 ,或 x=
4
9 。