中考数学命题研究图形的初步认识与三角形四边形矩形菱形正方形精讲试题

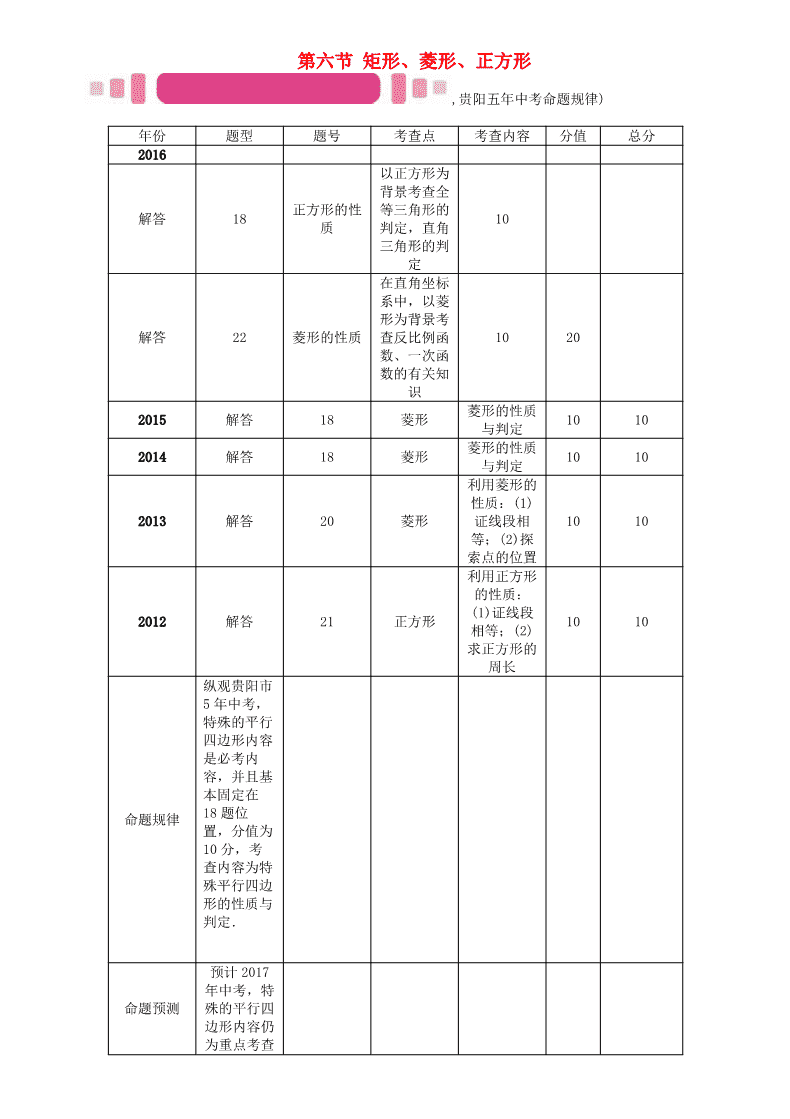
中考数学命题研究图形的初步认识与三角形四边形矩形菱形正方形精讲试题

第六节 矩形、菱形、正方形 ,贵阳五年中考命题规律) 年份 题型 题号 考查点 考查内容 分值 总分 2016 解答 18 正方形的性 质 以正方形为 背景考查全 等三角形的 判定，直角 三角形的判 定 10 解答 22 菱形的性质 在直角坐标 系中，以菱 形为背景考 查反比例函 数、一次函 数的有关知 识 10 20 2015 解答 18 菱形 菱形的性质 与判定 10 10 2014 解答 18 菱形 菱形的性质 与判定 10 10 2013 解答 20 菱形 利用菱形的 性质：(1) 证线段相 等；(2)探 索点的位置 10 10 2012 解答 21 正方形 利用正方形 的性质： (1)证线段 相等；(2) 求正方形的 周长 10 10 命题规律 纵观贵阳市 5 年中考， 特殊的平行 四边形内容 是必考内 容，并且基 本固定在 18 题位 置，分值为 10 分，考 查内容为特 殊平行四边 形的性质与 判定． 命题预测 预计 2017 年中考，特 殊的平行四 边形内容仍 为重点考查 内容，且以 解答题形式 出现，平时 训练要加大 对性质与判 定的训练力 度. ,贵阳五年中考真题及模拟) 菱形的性质与判定(4 次) 1．(2016 贵阳 22 题 10 分)如图，在平面直角坐标系中，菱形 OBCD 的边 OB 在 x 轴上，反比例函数 y＝ k x(x＞0) 的图象经过菱形对角线的交点 A，且与边 BC 交于点 F，点 A 的坐标为(4，2)． (1)求反比例函数的表达式； (2)求点 F 的坐标． 解：(1)∵反比例函数 y＝ k x的图象经过点 A，A 点的坐标为(4，2)，∴2＝ k 4，∴k＝8.∴反比例函数的表达式 为 y＝ 8 x；(2)过点 A 作 AM⊥x 轴于点 M，过点 C 作 CN⊥x 轴于点 N，由题意可知，CN＝2AM＝4，ON＝2OM＝8，∴点 C 的坐标为 C(8，4)，设 OB＝x，则 BC＝x，BN＝8－x，在 Rt△CNB 中，x2－(8－x)2＝42，解得 x＝5，∴点 B 的坐 标为 B(5，0)，设直线 BC 的函数表达式为 y＝k1x＋b，直线 BC 过点 B(5，0)，C(8，4)，∴ 5k1＋b＝0， 8k1＋b＝4，解得： 20 ，∴直线 BC 的表达式为 y＝ 4 3x－ 20 3 ，根据题意得方程组 8 ，解此方程组得： 4 ， x2＝－1， y2＝－8，∵点 F 在第一象限，∴点 F 的坐标为 F(6， 4 3)． 2．(2015 贵阳 18 题 10 分)如图，在 Rt△ABC 中，∠ACB＝90°，D 为 AB 的中点，且 AE∥CD，CE∥AB. (1)证明：四边形 ADCE 是菱形； (2)若∠B＝60°，BC＝6，求菱形 ADCE 的高．(计算结果保留根号) 解：(1)∵AE∥CD，CE∥AB，∴四边形 ADCE 是平行四边形，又∵∠ACB＝90°，D 是 AB 的中点，∴CD＝BD＝ AD，∴平行四边形 ADCE 是菱形；(2)如图，过点 D 作 DF⊥CE，垂足为点 F，则 DF 即为菱形 ADCE 的高，∵∠B＝ 60°，CD＝BD，∴△BCD 是等边三角形．∵CE∥AB，∴∠BCE＝120°，∴∠DCE＝60°，又∵CD＝BC＝6，∴在 Rt△CDF 中，DF＝3. 3．(2014 贵阳 18 题 10 分)如图，在 Rt△ABC 中，∠ACB＝90°，D，E 分别为 AB，AC 边上的中点，连接 DE， 将△ADE 绕点 E 旋转 180°得到△CFE，连接 AF. (1)求证：四边形 ADCF 是菱形； (2)若 BC＝8，AC＝6，求四边形 ABCF 的周长． 解：(1)∵将△ADE 绕点 E 旋转 180°得到△CFE.∴AE＝CE，DE＝FE，∴四边形 ADCF 为平行四边形．∵点 D， E 是 AB 与 AC 的中点，∴DE 是△ABC 的中位线，∴DE∥BC，∵∠ACB＝90°即 BC⊥AC，∴DF⊥AC，∴平行四边形 ADCF 为菱形；(2)∵在 Rt△ABC 中，BC＝8，AC＝6，∴AB＝10.∵点 D 是 AB 边上的中点，∴AD＝5.∵四边形 ADCF 为菱形，∴AF＝FC＝AD＝5，∴C 四边形 ABCF＝8＋10＋5＋5＝28. 4．(2013 贵阳 20 题 10 分)已知：如图，在菱形 ABCD 中，F 是 BC 上任意一点，连接 AF 交对角线 BD 于点 E， 连接 EC. (1)求证：AE＝EC； (2)当∠ABC＝60°，∠CEF＝60°时，点 F 在线段 BC 上的什么位置？说明理由． 解：(1)连接 AC，∵四边形 ABCD 为菱形，∴BD 垂直平分 AC，∴AE＝EC；(2)点 F 是线段 BC 的中点，理由如 下：易得△ABC 是等边三角形，∴∠BAC＝60°，∵AE＝EC，∠CEF＝60°，∴∠EAC＝ 1 2∠BAC＝30°，∴AF 是△ ABC 的角平分线，∵AF 交 BC 于点 F，∴AF 是△ABC 边 BC 上的中线，∴点 F 是线段 BC 的中点． 正方形的性质(2 次) 5．(2016 贵阳模拟卷②15 题)如图，在平面直角坐标系中，边长不等的正方形依次排列，每个正方形都有一 个顶点落在函数 y＝x 的图象上，从左向右第 3 个正方形中的一个顶点 A 的坐标为(8，4)，阴影三角形部分的面积 从左向右依次记为 S1，S2，S3，……，Sn，则 Sn 的值为__24n－5__．(用含 n 的代数式表示，n 为正整数) 6．(2012 贵阳 21 题 10 分)如图，在正方形 ABCD 中，等边三角形 AEF 的顶点 E、F 分别在 BC 和 CD 上． (1)求证：CE＝CF； (2)若等边三角形 AEF 的边长为 2，求正方形 ABCD 的周长． 解：(1)易证△ABE≌△ADF，∴BE＝DF，又 BC＝DC，∴BC－BE＝DC－DF，∴CE＝CF；(2)连接 AC，交 EF 于 G 点，易得 AC⊥EF，EC＝，设 BE＝x，则 AB＝x＋，在 Rt△ABE 中，(x＋)2＋x2＝4，∴x＝ 6 2，∴AB＝ 6 2＋＝ 6 2，∴正 方形的周长为 2＋2. 7．(2015 贵阳适应性考试)如图，E，F 是菱形 ABCD 对角线 AC 上的两点，且 AE＝CF. (1)求证：四边形 BEDF 是菱形； (2)若∠DAB＝60°，AD＝6，AE＝DE，求菱形 BEDF 的周长． 解：(1)∵菱形 ABCD，∴AB＝AD，对角线 AC 平分∠BAD，∴∠BAE＝∠DAE，又∵AE＝AE，∴△ABE≌△ADE， ∴BE＝ED.连接 BD 交 AC 于点 O，则 OD＝OB，OA＝OC，∵AE＝CF，∴OA－AE＝OC－CF，∴OE＝OF，∴四边形 BEDF 为平行四边形，∴▱ BEDF 为菱形；(2)在菱形 ABCD 中，连接 BD 交于 AC 于 O 点，∴DB⊥AC，又∵∠DAB＝60°， ∴∠DAE＝30°，∠ADB＝60°，∵AD＝6，∴在 Rt△ADO 中，DO＝ 1 2AD＝3，∵AE＝ED，∴∠DAE＝∠ADE，∠ADE＝ ∠EDO＝30°，在 Rt△DEO 中，可求得 DE＝2，∴菱形 BEDF 的周长为 8. ,中考考点清单) 矩形的性质与判定 1．定义：把有一个角是直角的平行四边形叫做矩形．如图(1)． 2．性质 文字描述 字母表示[参考图(1)] (1)对边平行且相等 AD 綊 BC，AB 綊 CD (2)四个内角都是直角 __∠DAB__＝∠ABC＝∠BCD＝∠CDA＝90° (3)两条对角线相等且互相平分 AC＝__BD__，OA＝OC＝OB＝OD (4)矩形既是中心对称图形，也是轴对称图 形 3.判定 文字描述 字母表示[参考图(1)] (1)有一个角是直角的平行四边形是矩形 若四边形 ABCD 是平行四边形，且∠BAD＝ 90°，则四边形 ABCD 是矩形 (2)有三个角是直角的四边形是矩形 若∠BAD＝∠ABC＝∠BCD＝90°，则四边形 ABCD 是矩形 (3)对角线相等的平行四边形是矩形 若 AC＝__BD__，且四边形 ABCD 是平行四边 形，则四边形 ABCD 是矩形 菱形的性质与判定(高频考点) 4．定义：把有一组邻边相等的平行四边形叫做菱形．如图(2) 5．性质 文字描述 字母表示[参考图(2)] (1)菱形的四条边都相等 AB＝__BC__＝CD＝DA (2)对角相等 ∠DAB＝∠DCB， ∠ADC＝__∠ABC__ (3)两条对角线互相垂直，且每条对角线平 分一组对角 __AC__⊥BD，∠DAC＝∠CAB＝∠DCA＝∠ ACB，∠ADB＝∠BDC＝∠ABD＝∠DBC (4)菱形既是中心对称图形，也是轴对称图 形 6．判定 文字描述 字母表示[参考图(2)] (1)有一组邻边相等的平行四边形是菱形 若四边形 ABCD 是平行四边形，且 AD＝AB， 则四边形 ABCD 是菱形 (2)四条边相等的四边形是菱形 若 AB＝BC＝CD＝DA，则四边形 ABCD 是菱形 (3)两条对角线互相垂直的平行四边形是菱 形 若 AC⊥BD，且四边形 ABCD 是平行四边形， 则四边形 ABCD 是菱形 正方形的性质与判定 7．定义：有一组邻边相等且有一个角是直角的平行四边形叫做正方形．如图(3) 8．性质 文字描述 字母表示[参考图(3)] (1)四条边都相等 即 AB＝BC＝CD＝DA (2)四个角都是 90° 即∠ABC＝∠ADC＝∠BCD＝∠BAD＝90° (3)对角线互相垂直平分且相等 即 AC⊥__BD__，OA＝OC＝OD＝OB (4)对角线平分一组对角 ∠DAC＝∠CAB＝∠DCA＝∠ACB＝∠ADB＝∠ BDC＝∠ABD＝∠DBC＝45° (5)正方形既是中心对称图形，也是轴对称 图形 9.判定 文字描述 字母表示[参考图(3)] (1)一组邻边相等且有一个角是直角的平行 四边形叫做正方形 若四边形 ABCD 是平行四边形，且 AB＝BC， ∠ADC＝90°，则四边形 ABCD 是正方形 (2)有一个角是直角的__菱形__是正方形 若∠ABC＝90°且四边形 ABCD 是菱形，则四 边形 ABCD 是正方形 (3)有一组邻边相等的矩形是正方形 若 AB＝BC，且四边形 ABCD 是矩形，则四边 形 ABCD 是正方形 (4)对角线互相垂直平分且相等的四边形是 正方形 若四边形 ABCD 中，AC⊥BD，AC 平分 BD，BD 平分 AC，AC＝BD，则四边形 ABCD 是正方形 ,中考重难点突破) 矩形的有关计算 【例 1】(2016 天津中考)如图，把一张矩形纸片 ABCD 沿对角线 AC 折叠，点 B 的对应点为 B′，AB′，DC 相 交于点 E，则下列结论一定正确的是( ) A．∠DAB′＝∠CAB′ B．∠ACD＝∠B′CD C．AD＝AE D．AE＝CE 【解析】由折叠的性质得：∠CAB′＝∠CAB.又∵AB∥CD，∴∠ACD＝∠CAB＝∠CAB′，∴AE＝CE. 【学生解答】D 1．(2016 海南中考)如图，矩形 ABCD 的顶点 A，C 分别在直线 a，b 上，且 a∥b，∠1＝60°，则∠2 的度数 为( C ) A．30° B．45° C．60° D．75° ,(第 1 题图)) ,(第 2 题图)) 2．(2016 南充中考)如图，对折矩形纸片 ABCD，使 AB 与 DC 重合得到折痕 EF，将纸片展平；再一次折叠，使 点 D 落到 EF 上点 G 处，并使折痕经过点 A，展开纸片后∠DAG 的大小为( C ) A．30° B．45° C．60° D．75° 3．(2016 巴中中考)如图，延长矩形 ABCD 的边 BC 至点 E，使 CE＝BD，连接 AE，如果∠ADB＝30°，则∠E＝ __15__°. 菱形的性质与判定 【例 2】(2016 南充中考)如图，菱形 ABCD 的周长是 8 cm，AB 的长是________cm. 【解析】菱形的四边形相等，故 AB＝8÷4＝2(cm)． 【学生解答】2 4．(2016 无锡中考)下列性质中，菱形具有而矩形不一定具有的是( C ) A．对角线相等 B．对角线互相平分 C．对角线互相垂直 D．邻边互相垂直 5．(2016 雅安中考)如图，四边形 ABCD 的四边相等，且面积为 120 cm2，对角线 AC＝24 cm，则四边形 ABCD 的周长为( A ) A．52 cm B．40 cm C．39 cm D．26 cm 6．(2016 遵义中考)在▱ ABCD 中，对角线 AC 与 BD 交于点 O.若增加一个条件，使▱ ABCD 成为菱形，下列给出 的条件不正确的是( C ) A．AB＝AD B．AC⊥BD C．AC＝BD D．∠BAC＝∠DAC 7．(2016 苏州中考)如图，在菱形 ABCD 中，对角线 AC，BD 相交于点 O，过点 D 作对角线 BD 的垂线交 BA 的延 长线于点 E. (1)证明：四边形 ACDE 是平行四边形； (2)AC＝8，BD＝6，求△ADE 的周长． 解：(1)∵四边形 ABCD 是菱形，∴AB∥CD，AC⊥BD，∴AE∥CD，∠AOB＝90°.又∵DE⊥BD，即∠EDB＝90°， ∴∠AOB＝∠EDB，∴DE∥AC，∴四边形 ACDE 是平行四边形；(2)∵四边形 ABCD 是菱形，AC＝8，BD＝6，∴AO＝ 4，DO＝3，AD＝CD＝5.又∵四边形 ACDE 是平行四边形，∴AE＝CD＝5，DE＝AC＝8，∴△ADE 的周长为 AD＋AE＋DE ＝5＋5＋8＝18. 正方形的性质与判定 【例 3】(2016 广东中考)如图，正方形 ABCD 的面积为 1，则以相邻两边中点的连线 EF 为边的正方形 EFGH 的 周长为( ) A. B．2 C.＋1 D．2＋1 【解析】由题意可知，正方形 ABCD 的边长为 1，则 CE＝ CF＝ 1 2.由勾股定理，得 EF＝＝ 1 ）2＝ 2 2，故正方形 EFGH 的周长为 2. 【学生解答】B 8．(2016 益阳中考)下列判断错误的是( D ) A．两组对边分别相等的四边形是平行四边形 B．四个内角都相等的四边形是矩形 C．四条边都相等的四边形是菱形 D．两条对角线垂直且平分的四边形是正方形 9．(2016 陕西中考)如图，在正方形 ABCD 中，连接 BD，点 O 是 BD 的中点，若 M，N 是 AD 上的两点，连接 MO，NO，并分别延长交边 BC 于 M′，N′两点，则图中全等三角形共有( C ) A．2 对 B．3 对 C．4 对 D．5 对 ,(第 9 题图)) ,(第 10 题图)) 10．(2016 西宁中考)如图，已知正方形 ABCD 的边长为 3，E，F 分别是 AB，BC 边上的点，且∠EDF＝45°.将 △DAE 绕点 D 逆时针旋转 90°，得到△DCM.若 AE＝1，则 FM 的长为__ 5 2__．