2018年高考真题——理科数学（天津卷）原卷版

2018年高考真题——理科数学（天津卷）原卷版

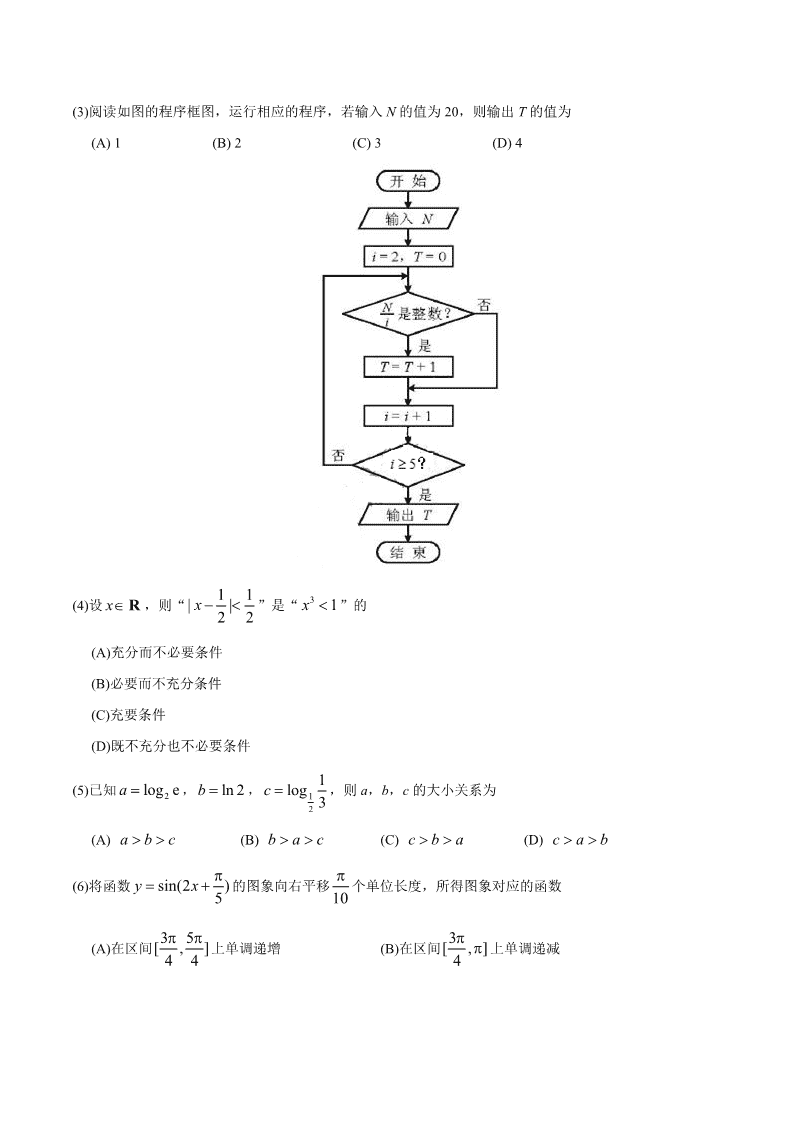
绝密★启用前 2018 年普通高等学校招生全国统一考试（天津卷） 数学（理工类） 本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共 150 分，考试用时 120 分钟。第Ⅰ卷 1 至 2 页，第Ⅱ卷 3 至 5 页。 答卷前，考生务必将自己的姓名、准考证号填写在答题考上，并在规定位置粘贴考试用条形码。答卷 时，考生务必将答案涂写在答题卡上，答在试卷上的无效。考试结束后，将本试卷和答题卡一并交回。 祝各位考生考试顺利！ 第 I 卷 注意事项： 1．每小题选出答案后，用铅笔将答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再 选涂其他答案标号。 2．本卷共 8 小题，每小题 5 分，共 40 分。 参考公式： 如果事件 A，B 互斥，那么 . 如果事件 A，B 相互独立，那么 . 棱柱的体积公式 ，其中 表示棱柱的底面面积， 表示棱柱的高. 棱锥的体积公式 ，其中 表示棱锥的底面面积， 表示棱锥的高. 一. 选择题：在每小题给出的四个选项中，只有一项是符合题目要求的. (1)设全集为 R，集合 ， ，则 (A) (B) (C) (D) (2)设变量 x，y 满足约束条件 则目标函数 的最大值为 (A) 6 (B) 19 (C) 21 (D) 45 ( ) ( ) ( )P A B P A P B  ( ) ( ) ( )P AB P A P B V Sh S h 1 3V Sh S h { 0 2}A x x   { 1}B x x  ( ) RIA Bð { 0 1}x x  { 0 1}x x  { 1 2}x x  { 0 2}x x  5, 2 4, 1, 0, x y x y x y y          3 5z x y  (3)阅读如图的程序框图，运行相应的程序，若输入 N 的值为 20，则输出 T 的值为 (A) 1 (B) 2 (C) 3 (D) 4 (4)设 ，则“ ”是“ ”的 (A)充分而不必要条件 (B)必要而不充分条件 (C)充要条件 (D)既不充分也不必要条件 (5)已知 ， ， ，则 a，b，c 的大小关系为 (A) (B) (C) (D) (6)将函数 的图象向右平移 个单位长度，所得图象对应的函数 (A)在区间 上单调递增 (B)在区间 上单调递减 xR 1 1| |2 2x   3 1x  2log ea ln 2b  1 2 1log 3c  a b c  b a c  c b a  c a b  sin(2 )5y x   10  3 5[ , ]4 4   3[ , ]4   (C)在区间 上单调递增 (D)在区间 上单调递减 (7)已知双曲线 的离心率为 2，过右焦点且垂直于 x 轴的直线与双曲线交于 A，B 两点. 设 A，B 到双曲线同一条渐近线的距离分别为 和 ，且 ，则双曲线的方程为 (A) (B) (C) (D) (8)如图，在平面四边形 ABCD 中， ， ， ， . 若点 E 为边 CD 上的动点，则 的最小值为 (A) (B) (C) (D) 第Ⅱ卷 注意事项： 1. 用黑色墨水的钢笔或签字笔将答案写在答题卡上。 2. 本卷共 12 小题，共 110 分。 二. 填空题：本大题共 6 小题，每小题 5 分，共 30 分。 (9) i 是虚数单位，复数 . (10) 在 的展开式中， 的系数为 . 5 3[ , ]4 2   3[ ,2 ]2   2 2 2 2 1( 0, 0)x y a ba b    1d 2d 1 2 6d d  2 2 14 12 x y  2 2 112 4 x y  2 2 13 9 x y  2 2 19 3 x y  AB BC AD CD 120BAD   1AB AD   uuur uur AE BE 21 16 3 2 25 16 3 6 7i 1 2i   51( ) 2 x x  2x (11) 已知正方体 的棱长为 1，除面 外，该正方体其余各面的中心分别为点 E，F， G，H，M(如图)，则四棱锥 的体积为 . (12)已知圆 的圆心为 C，直线 ( 为参数)与该圆相交于 A，B 两点，则 的面积为 . (13)已知 ，且 ，则 的最小值为 . (14)已知 ，函数 若关于 的方程 恰有 2 个互异的实数解， 则 的取值范围是 . 三.解答题：本大题共 6 小题，共 80 分. 解答应写出文字说明，证明过程或演算步骤. （15）（本小题满分 13 分） 在 中，内角 A，B，C 所对的边分别为 a，b，c.已知 . （I）求角 B 的大小；学科*网 （II）设 a=2，c=3，求 b 和 的值. (16)(本小题满分 13 分) 已知某单位甲、乙、丙三个部门的员工人数分别为 24，16，16. 现采用分层抽样的方法从中抽取 7 人， 进行睡眠时间的调查. （I）应从甲、乙、丙三个部门的员工中分别抽取多少人？ 1 1 1 1ABCD A B C D ABCD M EFGH 2 2 2 0x y x   21 ,2 23 2        x t y t t ABC△ ,a bR 3 6 0a b   12 8 a b 0a  2 2 2 , 0,( ) 2 2 , 0. x ax a xf x x ax a x         x ( )f x ax a ABC△ sin cos( )6b A a B   sin(2 )A B （II）若抽出的 7 人中有 4 人睡眠不足，3 人睡眠充足，现从这 7 人中随机抽取 3 人做进一步的身体检 查. （i）用 X 表示抽取的 3 人中睡眠不足的员工人数，求随机变量 X 的分布列与数学期望； （ii）设 A 为事件“抽取的 3 人中，既有睡眠充足的员工，也有睡眠不足的员工”，求事件 A 发生 的概率. (17)(本小题满分 13 分) 如 图 ， 且 AD=2BC ， , 且 EG=AD ， 且 CD=2FG ， ，DA=DC=DG=2. （I）若 M 为 CF 的中点，N 为 EG 的中点，求证： ； （II）求二面角 的正弦值；学.科网 （III）若点 P 在线段 DG 上，且直线 BP 与平面 ADGE 所成的角为 60°，求线段 DP 的长. (18)(本小题满分 13 分) 设 是 等 比 数 列 ， 公 比 大 于 0 ， 其 前 n 项 和 为 ， 是 等 差 数 列 . 已 知 ， ， ， . （I）求 和 的通项公式； （II）设数列 的前 n 项和为 ， （i）求 ； （ii）证明 . (19)(本小题满分 14 分) AD BC∥ AD CD EG AD∥ CD FG∥ DG ABCD 平面 MN CDE∥平面 E BC F  { }na ( )nS n N { }nb 1 1a  3 2 2a a  4 3 5a b b  5 4 62a b b  { }na { }nb { }nS ( )nT n N nT 2 2 1 ( ) 2 2( )( 1)( 2) 2 nn k k k k T b b nk k n          N 设椭圆 (a>b>0) 的左焦点为 F ，上顶点为 B. 已知椭圆的离心率为 ，点 A 的坐标为 ，且 . （I）求椭圆的方程； （II）设直线 l： 与椭圆在第一象限的交点为 P，且 l 与直线 AB 交于点 Q. 若 (O 为原点) ，求 k 的值. (20)(本小题满分 14 分) 已知函数 ， ，其中 a>1. （I）求函数 的单调区间； （II）若曲线 在点 处的切线与曲线 在点 处的切线平行，证明 ； （III）证明当 时，存在直线 l，使 l 是曲线 的切线，也是曲线 的切线. 2 2 2 2 1x x a b  5 3 ( ,0)b 6 2FB AB  ( 0)y kx k  5 2 sin4 AQ AOQPQ   ( ) xf x a ( ) logag x x ( ) ( ) lnh x f x x a  ( )y f x 1 1( , ( ))x f x ( )y g x 2 2( , ( ))x g x 1 2 2ln ln( ) ln ax g x a   1 eea  ( )y f x ( )y g x 参考答案： 一、选择题：本题考查基本知识和基本运算．每小题 5 分，满分 40 分． （1）B （2）C （3）B （4）A （5）D （6）A （7）C （8）A 二、填空题：本题考查基本知识和基本运算．每小题 5 分，满分 30 分． （9）4–i （10） （11） （12） （13） （14） 三、解答题 （15）本小题主要考查同角三角函数的基本关系，两角差的正弦与余弦公式，二倍角的正弦与余弦公式， 以及正弦定理、余弦定理等基础知识，考查运算求解能力．满分 13 分． （Ⅰ）解：在△ABC 中，由正弦定理 ，可得 ，又由 ， 得 ，即 ，可得 ．又因为 ，可得 B= ． （Ⅱ）解：在△ABC 中，由余弦定理及 a=2，c=3，B= ，有 ，故 b= ． 由 ，可得 ．因为 a= ，于是 sin= ． 所以，二面角 E–BC–F 的正弦值为 ． （ Ⅲ ） 解 ： 设 线 段 DP 的 长 为 h （ h ∈ ［ 0 ， 2 ］ ） ， 则 点 P 的 坐 标 为 （ 0 ， 0 ， h ） ， 可 得 ． 易知， =（0，2，0）为平面 ADGE 的一个法向量，故 ， 由题意，可得 =sin60°= ，解得 h= ∈［0，2］． 所以线段 的长为 . （18）本小题主要考查等差数列的通项公式，等比数列的通项公式及前 n 项和公式等基础知识.考查等差数 列求和的基本方法和运算求解能力.满分 13 分. （I）解：设等比数列 的公比为 q.由 可得 . 因为 ，可得 ，故 . 设等差数列 的公差为 d，由 ，可得 由 ， 可得 从而 故 所以数列 的通项公式为 ，数列 的通项公式为 （II）（i）由（I），有 ，故 . （ii）证明：因为 0 0 BC BF        ， ， m m 0 2 0 x y z      ， ， 3 10 | || | 10  m n m n 10 10 10 10 ( 1 2 )BP h   ， ， DC 2 2cos 5 BP DC BP DC BP DC h              2 2 5h  3 2 3 3 DP 3 3 { }na 1 3 21, 2,a a a   2 2 0q q   0q  2q  12n na  { }nb 4 3 5a b b  1 3 4.b d  5 4 62a b b  13 13 16,b d  1 1, 1,b d  .nb n { }na 12n na  { }nb .nb n 1 2 2 11 2 n n nS    1 1 1 2 (1 2 )(2 1) 2 2 21 2 nn n k k n n k k T n n n              ， 所以， . （19）本小题主要考查椭圆的标准方程和几何性质、直线方程等基础知识．考查用代数方法研究圆锥曲线 的性质．考查运算求解能力，以及用方程思想解决问题的能力．满分 14 分． （Ⅰ）解：设椭圆的焦距为 2c，由已知知 ，又由 a2=b2+c2 ，可得 2a=3b．由已知可得， ， ，由 ，可得 ab=6，从而 a=3，b=2． 所以，椭圆的方程为 ． （ Ⅱ ） 解 ： 设 点 P 的 坐 标 为 （ x1 ， y1 ） ， 点 Q 的 坐 标 为 （ x2 ， y2 ） ． 由 已 知 有 y1>y2>0 ， 故 ． 又 因 为 ， 而 ∠ OAB= ， 故 ． 由 ，可得 5y1=9y2． 由 方 程 组 消 去 x， 可 得 ． 易 知 直 线 AB 的 方 程 为 x+y–2=0， 由 方 程 组 消 去 x ， 可 得 ． 由 5y1=9y2 ， 可 得 5 （ k+1 ） = ， 两 边 平 方 ， 整 理 得 ，解得 ，或 ． 所以，k 的值为 （20）本小题主要考查导数的运算、导数的几何意义、运用导数研究指数函数与对数函数的性质等基础知 识和方法.考查函数与方程思想、化归思想.考查抽象概括能力、综合分析问题和解决问题的能力.满分 14 分. （I）解：由已知， ，有 . 令 ，解得 x=0. 由 a>1，可知当 x 变化时， ， 的变化情况如下表： 1 1 2 1 2( ) (2 2 2) 2 2 2 ( 1)( 2) ( 1)( 2) ( 1)( 2) 2 1 k k k k k k+ kT +b b k k k k k k k k k k k k                   3 2 4 3 2 1 2 2 1 ( ) 2 2 2 2 2 2 2( ) ( ) ( ) 2( 1)( 2) 3 2 4 3 2 1 2 n n nn k k k k T b b k k n n n                     2 2 5 9 c a  FB a 2AB b 6 2FB AB  2 2 19 4 x y  1 2sinPQ AOQ y y   2 sin yAQ OAB  π 4 22AQ y 5 2 sin4 AQ AOQPQ   2 2 19 4 y kx x y    ， ， 1 2 6 9 4 ky k   2 0 y kx x y      ， ， 2 2 1 ky k  23 9 4k  256 50 11 0k k   1 2k  11 28k  1 11 2 28 或 ． ( ) lnxh x a x a  ( ) ln lnxh x a a a   ( ) 0h x  ( )h x ( )h x x 0 0 + 极小值 所以函数 的单调递减区间 ，单调递增区间为 . （II）证明：由 ，可得曲线 在点 处的切线斜率为 . 由 ，可得曲线 在点 处的切线斜率为 . 因为这两条切线平行，故有 ，即 . 两边取以 a 为底的对数，得 ，所以 . （III）证明：曲线 在点 处的切线 l1： . 曲线 在点 处的切线 l2： . 要证明当 时，存在直线 l，使 l 是曲线 的切线，也是曲线 的切线，只需证明 当 时，存在 ， ，使得 l1 和 l2 重合.学*科网 即只需证明当 时，方程组 有解， 由①得 ，代入②，得 . ③ 因此，只需证明当 时，关于 x1 的方程③有实数解. 设函数 ，即要证明当 时，函数 存在零点. ，可知 时， ； 时， 单调递减，又 ， ，故存在唯一的 x0，且 x0>0，使得 ，即 ( ,0) (0, ) ( )h x  ( )h x   ( )h x ( ,0) (0, ) ( ) lnxf x a a  ( )y f x 1 1( , ( ))x f x 1 lnxa a 1( ) lng x x a   ( )y g x 2 2( , ( ))x g x 2 1 lnx a 1 2 1ln ln xa a x a 1 2 2 (ln ) 1xx a a  2 1 2log 2log ln 0a x x a   1 2 2ln ln( ) ln ax g x a   ( )y f x 1 1( , )xx a 1 1 1ln ( )x xy a a a x x    ( )y g x 2 2( ,log )ax x 2 2 2 1log ( )lnay x x xx a    1 eea  ( )y f x ( )y g x 1 eea  1 ( , )x    2 (0, )x   1 eea  1 1 1 2 1 2 1ln ln 1ln log ln x x x a a a x a a x a a x a       ① ② 12 2 1 (ln )xx a a 1 1 1 1 1 2ln lnln 0ln ln x x aa x a a x a a     1 eea  1 2ln ln( ) ln ln ln x x au x a xa a x a a     1 eea  ( )y u x 2( ) 1 (ln ) xu x a xa   ( ,0)x  ( ) 0u x  (0, )x  ( )u x (0) 1 0u   2 1 (ln ) 2 1 1 0(ln ) au aa        0( ) 0u x  . 由此可得 在 上单调递增，在 上单调递减. 在 处取得极大值 . 因为 ，故 ， 所以 . 下面证明存在实数 t，使得 . 由（I）可得 ， 当 时， 有 ， 所以存在实数 t，使得 因此，当 时，存在 ，使得 . 所以，当 时，存在直线 l，使 l 是曲线 的切线，也是曲线 的切线. 02 01 (ln ) 0xa x a  ( )u x 0( , )x 0( , )x  ( )u x 0x x 0( )u x 1 eea  ln(ln ) 1a   0 0 0 0 0 02 0 1 2ln ln 1 2ln ln 2 2ln ln( ) ln 0ln ln (ln ) ln ln x x a a au x a x a a x xa a x a a a           ( ) 0u t  1 lnxa x a  1 lnx a 2 21 2ln ln 1 2ln ln( ) (1 ln )(1 ln ) (ln ) 1ln ln ln ln a au x x a x a x a x xa a a a            ( ) 0u t  1 eea  1 ( , )x    1( ) 0u x  1 eea  ( )y f x ( )y g x