高中数学必修5教案：第一章 解三角形

高中数学必修5教案：第一章 解三角形

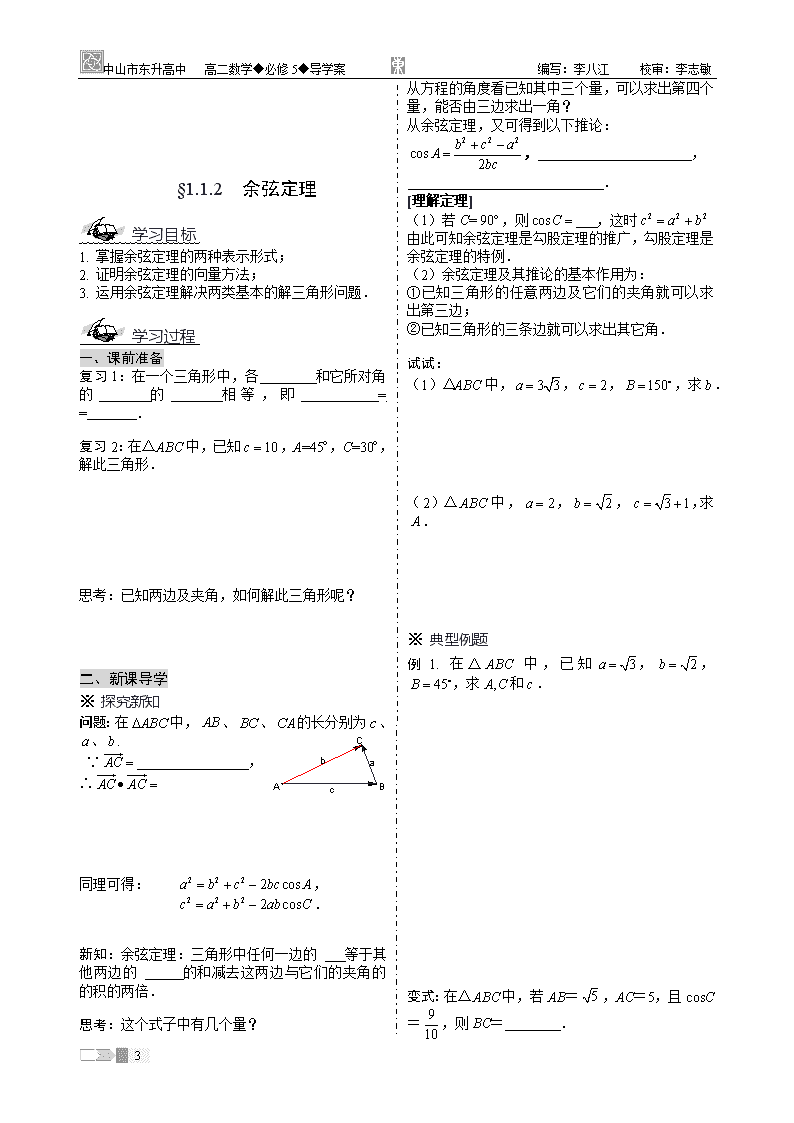
中山市东升高中 高二数学◆必修5◆导学案 编写：李八江 校审：李志敏 ‎§1.1.1 正弦定理 ‎ 学习目标 ‎ ‎1. 掌握正弦定理的内容；‎ ‎2. 掌握正弦定理的证明方法；‎ ‎3. 会运用正弦定理解斜三角形的两类基本问题．‎ ‎ 学习过程 ‎ 一、课前准备 试验：固定ABC的边CB及B，使边AC绕着顶点C转动．‎ 思考：C的大小与它的对边AB的长度之间有怎样的数量关系？‎ 显然，边AB的长度随着其对角C的大小的增大而 ．能否用一个等式把这种关系精确地表示出来？ ‎ 二、新课导学 ‎※ 学习探究 探究1：在初中，我们已学过如何解直角三角形，下面就首先来探讨直角三角形中，角与边的等式关系. 如图，在RtABC中，设BC=a，AC=b，AB=c， ‎ 根据锐角三角函数中正弦函数的定义，‎ 有，，又， ‎ 从而在直角三角形ABC中，． ‎ ‎(‎ 探究2：那么对于任意的三角形，以上关系式是否仍然成立？‎ 可分为锐角三角形和钝角三角形两种情况：‎ 当ABC是锐角三角形时，设边AB上的高是CD，根据任意角三角函数的定义，‎ 有CD=，则， ‎ 同理可得， ‎ 从而．‎ ‎ ‎ 类似可推出，当ABC是钝角三角形时，以上关系式仍然成立．请你试试导.‎ 新知：正弦定理 在一个三角形中，各边和它所对角的 的比相等，即 ‎．‎ 试试：‎ ‎（1）在中，一定成立的等式是（ ）．‎ A． B.‎ C. D.‎ ‎（2）已知△ABC中，a＝4，b＝8，∠A＝30°，则∠B等于 ．‎ ‎[理解定理]‎ ‎（1）正弦定理说明同一三角形中，边与其对角的正弦成正比，且比例系数为同一正数，即存在正数k使， ，；‎ ‎（2）等价于 ，，．‎ ‎（3）正弦定理的基本作用为：‎ ‎①已知三角形的任意两角及其一边可以求其他边，如； ．‎ ‎②已知三角形的任意两边与其中一边的对角可以求其他角的正弦值，‎ 如； ．‎ ‎（4）一般地，已知三角形的某些边和角，求其它的边和角的过程叫作解三角形．‎ ‎※ 典型例题 例1. 在中，已知，，cm，解三角形．‎ 19‎ 中山市东升高中 高二数学◆必修5◆导学案 编写：李八江 校审：李志敏 变式：在中，已知，，cm，解三角形．‎ 例2. 在．‎ 变式：在．‎ 三、总结提升 ‎※ 学习小结 ‎1. 正弦定理：‎ ‎2. 正弦定理的证明方法：①三角函数的定义，‎ 还有 ②等积法，③外接圆法，④向量法.‎ ‎3．应用正弦定理解三角形：‎ ‎ ①已知两角和一边；‎ ‎②已知两边和其中一边的对角．‎ ‎※ 知识拓展 ‎，其中为外接圆直径.‎ ‎ 学习评价 ‎ ‎※ 自我评价 你完成本节导学案的情况为（ ）.‎ ‎ A. 很好 B. 较好 C. 一般 D. 较差 ‎※ 当堂检测（时量：5分钟 满分：10分）计分：‎ ‎1. 在中，若，则是（ ）.‎ A．等腰三角形 B．等腰三角形或直角三角形 C．直角三角形 D．等边三角形 ‎2. 已知△ABC中，A∶B∶C＝1∶1∶4，‎ 则a∶b∶c等于（ ）.‎ ‎　A．1∶1∶4 B．1∶1∶2　 C．1∶1∶ D．2∶2∶‎ ‎3. 在△ABC中，若，则与的大小关系为（ ）.‎ A. B. ‎ C. ≥ D. 、的大小关系不能确定 ‎4. 已知ABC中，，则= ．‎ ‎5. 已知ABC中，A，，则 ‎= ．‎ ‎　 ‎ ‎ 课后作业 ‎ ‎1. 已知△ABC中，AB＝6，∠A＝30°，∠B＝，解此三角形．‎ ‎2. 已知△ABC中，sinA∶sinB∶sinC＝k∶(k＋1)∶2k (k≠0)，求实数k的取值范围为．‎ 19‎ 中山市东升高中 高二数学◆必修5◆导学案 编写：李八江 校审：李志敏 ‎§1.1.2 余弦定理 ‎ 学习目标 ‎ ‎1. 掌握余弦定理的两种表示形式；‎ ‎2. 证明余弦定理的向量方法；‎ ‎3. 运用余弦定理解决两类基本的解三角形问题．‎ ‎ 学习过程 ‎ 一、课前准备 复习1：在一个三角形中，各 和它所对角的 的 相等，即 = = ．‎ 复习2：在△ABC中，已知，A=45°，C=30°，解此三角形．‎ 思考：已知两边及夹角，如何解此三角形呢？‎ 二、新课导学 ‎※ 探究新知 问题：在中，、、的长分别为、、.‎ ‎ ∵ ，‎ ‎∴‎ 同理可得： ，‎ ‎ ．‎ 新知：余弦定理：三角形中任何一边的 等于其他两边的 的和减去这两边与它们的夹角的 的积的两倍．‎ 思考：这个式子中有几个量？‎ 从方程的角度看已知其中三个量，可以求出第四个量，能否由三边求出一角？‎ 从余弦定理，又可得到以下推论：‎ ‎， ，‎ ‎ ．‎ ‎[理解定理]‎ ‎（1）若C=，则 ，这时 由此可知余弦定理是勾股定理的推广，勾股定理是余弦定理的特例．‎ ‎（2）余弦定理及其推论的基本作用为：‎ ‎①已知三角形的任意两边及它们的夹角就可以求出第三边；‎ ‎②已知三角形的三条边就可以求出其它角．‎ 试试：‎ ‎（1）△ABC中，，，，求．‎ ‎（2）△ABC中，，，，求．‎ ‎※ 典型例题 例1. 在△ABC中，已知，，，求和．‎ 变式：在△ABC中，若AB＝，AC＝5，且cosC＝，则BC＝________．‎ 19‎ 中山市东升高中 高二数学◆必修5◆导学案 编写：李八江 校审：李志敏 例2. 在△ABC中，已知三边长，，，求三角形的最大内角．‎ 变式：在ABC中，若，求角A．‎ 三、总结提升 ‎※ 学习小结 ‎1. 余弦定理是任何三角形中边角之间存在的共同规律，勾股定理是余弦定理的特例；‎ ‎2. 余弦定理的应用范围：‎ ‎① 已知三边，求三角；‎ ‎② 已知两边及它们的夹角，求第三边．‎ ※ 知识拓展 在△ABC中，‎ 若，则角是直角；‎ 若，则角是钝角；‎ 若，则角是锐角．‎ ‎ 学习评价 ‎ ‎※ 自我评价 你完成本节导学案的情况为（ ）.‎ ‎ A. 很好 B. 较好 C. 一般 D. 较差 ‎※ 当堂检测（时量：5分钟 满分：10分）计分：‎ ‎1. 已知a＝，c＝2，B＝150°，则边b的长为（ ）.‎ ‎ A. B. C. D. ‎ ‎2. 已知三角形的三边长分别为3、5、7，则最大角为（ ）.‎ A． B． C． D．‎ ‎3. 已知锐角三角形的边长分别为2、3、x，则x的取值范围是（ ）.‎ A． B．＜x＜5　‎ ‎　C． 2＜x＜ D．＜x＜5‎ ‎4. 在△ABC中，||＝3，||＝2，与的夹角为60°，则|－|＝________．‎ ‎5. 在△ABC中，已知三边a、b、c满足 ‎，则∠C等于 ．‎ ‎ 课后作业 ‎ ‎1. 在△ABC中，已知a＝7，b＝8，cosC＝，求最大角的余弦值．‎ ‎2. 在△ABC中，AB＝5，BC＝7，AC＝8，求的值.‎ 19‎ 中山市东升高中 高二数学◆必修5◆导学案 编写：李八江 校审：李志敏 ‎§1.1 正弦定理和余弦定理（练习）‎ ‎ 学习目标 ‎ ‎1. 进一步熟悉正、余弦定理内容；‎ ‎2. 掌握在已知三角形的两边及其中一边的对角解三角形时，有两解或一解或无解等情形．‎ ‎ 学习过程 ‎ 一、课前准备 复习1：在解三角形时 已知三边求角，用 定理；‎ 已知两边和夹角，求第三边，用 定理；‎ 已知两角和一边，用 定理．‎ 复习2：在△ABC中，已知 A＝，a＝25，b＝50，解此三角形．‎ 二、新课导学 ‎※ 学习探究 探究：在△ABC中，已知下列条件，解三角形.‎ ① A＝，a＝25，b＝50； ‎ ② A＝，a＝，b＝50； ‎ ③ A＝，a＝50，b＝50.‎ 思考：解的个数情况为何会发生变化？‎ 新知：用如下图示分析解的情况（A为锐角时）．‎ 试试：‎ ‎1. 用图示分析（A为直角时）解的情况？‎ ‎2．用图示分析（A为钝角时）解的情况？‎ ‎※ 典型例题 例1. 在ABC中，已知，，，试判断此三角形的解的情况．‎ 变式：在ABC中，若，，，则符合题意的b的值有_____个．‎ 19‎ 中山市东升高中 高二数学◆必修5◆导学案 编写：李八江 校审：李志敏 例2. 在ABC中，，，，求的值．‎ 变式：在ABC中，若，，且，求角C．‎ 三、总结提升 ‎※ 学习小结 ‎1. 已知三角形两边及其夹角（用余弦定理解决）；‎ ‎2. 已知三角形三边问题（用余弦定理解决）；‎ ‎3. 已知三角形两角和一边问题（用正弦定理解决）；‎ ‎4. 已知三角形两边和其中一边的对角问题（既可用正弦定理，也可用余弦定理，可能有一解、两解和无解三种情况）．‎ ‎※ 知识拓展 在ABC中，已知，讨论三角形解的情况 ：①当A为钝角或直角时，必须才能有且只有一解；否则无解；‎ ‎②当A为锐角时，‎ 如果≥，那么只有一解；‎ 如果，那么可以分下面三种情况来讨论：‎ ‎（1）若，则有两解；‎ ‎（2）若，则只有一解；‎ ‎（3）若，则无解．‎ ‎ 学习评价 ‎ ‎※ 自我评价 你完成本节导学案的情况为（ ）.‎ ‎ A. 很好 B. 较好 C. 一般 D. 较差 ‎※ 当堂检测（时量：5分钟 满分：10分）计分：‎ ‎1. 已知a、b为△ABC的边，A、B分别是a、b的对角，且，则的值=（ ）.‎ A. B. C. D. ‎ ‎2. 已知在△ABC中，sinA∶sinB∶sinC＝3∶5∶7，那么这个三角形的最大角是（ ）.‎ ‎　 A．135° B．90°　 C．120° D．150°‎ ‎3. 如果将直角三角形三边增加同样的长度，则新三角形形状为（ ）.‎ A．锐角三角形 B．直角三角形 C．钝角三角形 D．由增加长度决定 ‎4. 在△ABC中，sinA:sinB:sinC＝4:5:6，则cosB＝ ．‎ ‎5. 已知△ABC中，，试判断△ABC的形状 ．‎ ‎ 课后作业 ‎ ‎1. 在ABC中，，，，如果利用正弦定理解三角形有两解，求x的取值范围．‎ ‎2. 在ABC中，其三边分别为a、b、c，且满足，求角C．‎ 19‎ 中山市东升高中 高二数学◆必修5◆导学案 编写：李八江 校审：李志敏 ‎§1.2应用举例—①测量距离 ‎ ‎ 学习目标 ‎ 能够运用正弦定理、余弦定理等知识和方法解决一些有关测量距离的实际问题 ‎ 学习过程 ‎ 一、课前准备 复习1：在△ABC中，∠C＝60°，a＋b＝，c＝2，则∠A为 . ‎ 复习2：在△ABC中，sinA＝，判断三角形的形状.‎ 二、新课导学 ‎※ 典型例题 例1. 如图，设A、B两点在河的两岸，要测量两点之间的距离，测量者在A的同侧，在所在的河岸边选定一点C，测出AC的距离是55m，BAC=，ACB=. 求A、B两点的距离(精确到0.1m). ‎ 提问1：ABC中，根据已知的边和对应角，运用哪个定理比较适当？‎ 提问2：运用该定理解题还需要那些边和角呢？‎ 分析：这是一道关于测量从一个可到达的点到一个不可到达的点之间的距离的问题 题目条件告诉了边AB的对角，AC为已知边，‎ 再根据三角形的内角和定理很容易根据两个已知角算出AC的对角，‎ 应用正弦定理算出AB边. ‎ 新知1：基线 在测量上，根据测量需要适当确定的 叫基线. ‎ 例2. 如图，A、B两点都在河的对岸（不可到达），设计一种测量A、B两点间距离的方法. ‎ 分析：这是例1的变式题，研究的是两个 的点之间的距离测量问题. ‎ 首先需要构造三角形，所以需要确定C、D两点. ‎ 根据正弦定理中已知三角形的任意两个内角与一边既可求出另两边的方法，分别求出AC和BC，‎ 再利用余弦定理可以计算出AB的距离. ‎ 19‎ 中山市东升高中 高二数学◆必修5◆导学案 编写：李八江 校审：李志敏 变式：若在河岸选取相距40米的C、D两点，测得BCA=60°，ACD=30°，CDB=45°，BDA =60°.‎ 练：两灯塔A、B与海洋观察站C的距离都等于a km，灯塔A在观察站C的北偏东30°，灯塔B在观察站C南偏东60°，则A、B之间的距离为多少？‎ 三、总结提升 ‎※ 学习小结 ‎1. 解斜三角形应用题的一般步骤：‎ ‎（1）分析：理解题意，分清已知与未知，画出示意图 ‎（2）建模：根据已知条件与求解目标，把已知量与求解量尽量集中在有关的三角形中，建立一个解斜三角形的数学模型；‎ ‎（3）求解：利用正弦定理或余弦定理有序地解出三角形，求得数学模型的解 ‎（4）检验：检验上述所求的解是否符合实际意义，从而得出实际问题的解.‎ ‎2．基线的选取：‎ 测量过程中，要根据需要选取合适的基线长度，使测量具有较高的精确度. ‎ ‎ 学习评价 ‎ ‎※ 自我评价 你完成本节导学案的情况为（ ）.‎ ‎ A. 很好 B. 较好 C. 一般 D. 较差 ‎※ 当堂检测（时量：5分钟 满分：10分）计分：‎ P A C ‎1. 水平地面上有一个球，现用如下方法测量球的大小，用锐角的等腰直角三角板的斜边紧靠球面，P为切点，一条直角边AC紧靠地面，并使三角板与地面垂直，如果测得PA=5cm，则球的半径等于（ ）.‎ ‎ A．5cm B．‎ C．‎ D．6cm ‎2. 台风中心从A地以每小时20千米的速度向东北方向移动，离台风中心30千米内的地区为危险区，城市B在A的正东40千米处，B城市处于危险区内的时间为（ ）.‎ A．0.5小时　　 　B．1小时　　‎ C．1.5小时　　 　D．2小时 ‎3. 在中，已知，‎ 则的形状（ ）.‎ A.等腰三角形 B.直角三角形 ‎ C.等腰直角三角形 D.等腰三角形或直角三角形 ‎4.在中，已知，，，则的值是 ．‎ ‎5. 一船以每小时15km的速度向东航行，船在A处看到一个灯塔B在北偏东，行驶４h后，船到达C处，看到这个灯塔在北偏东，这时船与灯塔的距离为 km．‎ ‎ 课后作业 ‎ ‎1. 隔河可以看到两个目标，但不能到达，在岸边选取相距km的C、D两点，并测得∠ACB＝75°，∠BCD＝45°，∠ADC＝30°，∠ADB＝45°，A、B、C、D在同一个平面，求两目标A、B间的距离.‎ ‎2. 某船在海面A处测得灯塔C与A相距海里，且在北偏东方向；测得灯塔B与A相距 19‎ 中山市东升高中 高二数学◆必修5◆导学案 编写：李八江 校审：李志敏 海里，且在北偏西方向. 船由向正北方向航行到D处，测得灯塔B在南偏西方向. 这时灯塔C与D相距多少海里？‎ ‎§1.2应用举例—②测量高度 ‎ ‎ 学习目标 ‎ ‎1. 能够运用正弦定理、余弦定理等知识和方法解决一些有关底部不可到达的物体高度测量的问题；‎ ‎2. 测量中的有关名称.‎ ‎ 学习过程 ‎ 一、课前准备 复习1：在ABC中，，则ABC的形状是怎样？‎ 复习2：在ABC中，、b、c分别为A、B、C的对边，若=1:1:，求A:B:C的值.‎ 二、新课导学 ‎※ 学习探究 新知：坡度、仰角、俯角、方位角 方位角---从指北方向顺时针转到目标方向线的水平转角 ；‎ 坡度---沿余坡向上的方向与水平方向的夹角；‎ 仰角与俯角---视线与水平线的夹角当视线在水平线之上时，称为仰角；当视线在水平线之下时，称为俯角. ‎ 探究：AB是底部B不可到达的一个建筑物，A为建筑物的最高点，设计一种测量建筑物高度AB的方法. ‎ 分析：选择基线HG，使H、G、B三点共线，‎ 要求AB，先求AE 在中，可测得角 ，关键求AC 在中，可测得角 ，线段 ，又有 故可求得AC ‎※ 典型例题 例1. 如图，在山顶铁塔上B处测得地面上一点A的俯角=54，在塔底C处测得A处的俯角=50. 已知铁塔BC部分的高为27.3 m，求出山高CD(精确到1 m)‎ 19‎ 中山市东升高中 高二数学◆必修5◆导学案 编写：李八江 校审：李志敏 例2. 如图，一辆汽车在一条水平的公路上向正东行驶，到A处时测得公路南侧远处一山顶D在东偏南15的方向上，行驶5km后到达B处，测得此山顶在东偏南25的方向上，仰角为8，求此山的高度CD.‎ 问题1：‎ 欲求出CD，思考在哪个三角形中研究比较适合呢？‎ 问题2：‎ 在BCD中，已知BD或BC都可求出CD，根据条件，易计算出哪条边的长？‎ 变式：某人在山顶观察到地面上有相距2500米的A、B两个目标，测得目标A在南偏西57°，俯角是60°，测得目标B在南偏东78°，俯角是45°，试求山高.‎ 三、总结提升 ‎※ 学习小结 利用正弦定理和余弦定理来解题时，要学会审题及根据题意画方位图，要懂得从所给的背景资料中进行加工、抽取主要因素，进行适当的简化. ‎ ‎※ 知识拓展 在湖面上高h处，测得云之仰角为，湖中云之影的俯角为，则云高为.‎ ‎ 学习评价 ‎ ‎※ 自我评价 你完成本节导学案的情况为（ ）.‎ ‎ A. 很好 B. 较好 C. 一般 D. 较差 ‎※ 当堂检测（时量：5分钟 满分：10分）计分：‎ ‎1. 在ABC中，下列关系中一定成立的是（ ）.‎ A． B．‎ C． D．‎ ‎2. 在ABC中，AB=3，BC=，AC=4，则边AC上的高为（ ）.‎ A． B． C． D．‎ ‎3. D、C、B在地面同一直线上，DC=100米，从D、C两地测得A的仰角分别为和，则A点离地面的高AB等于（ ）米．‎ A．100 B．‎ C．50 D．50‎ ‎4. 在地面上点，测得一塔塔顶和塔基的仰角分别是和，已知塔基高出地面，则塔身的高为_________．‎ ‎5. 在ABC中，，，且三角形有两解，则A的取值范围是 ．‎ ‎ 课后作业 ‎ ‎1. 为测某塔AB的高度，在一幢与塔AB相距20m的楼的楼顶处测得塔顶A的仰角为30°，测得塔基B的俯角为45°，则塔AB的高度为多少m？‎ 19‎ 中山市东升高中 高二数学◆必修5◆导学案 编写：李八江 校审：李志敏 ‎2. 在平地上有A、B两点，A在山的正东，B在山的东南，且在A的南25°西300米的地方，在A侧山顶的仰角是30°，求山高.‎ ‎§1.2应用举例—③测量角度 ‎ 学习目标 ‎ 能够运用正弦定理、余弦定理等知识和方法解决一些有关计算角度的实际问题.‎ ‎ 学习过程 ‎ 一、课前准备 复习1：在中，已知，，且，求.‎ 复习2：设的内角A，B，C的对边分别为a，b，c，且A=，，求的值.‎ 二、新课导学 ‎※ 典型例题 例1. 如图，一艘海轮从A出发，沿北偏东75的方向航行67.5 n mile后到达海岛B，然后从B出发，沿北偏东32的方向航行54.0 n mile后达到海岛C.如果下次航行直接从A出发到达C，此船应该沿怎样的方向航行，需要航行多少距离?(角度精确到0.1，距离精确到0.01n mile)‎ 分析：‎ 首先由三角形的内角和定理求出角ABC，‎ 然后用余弦定理算出AC边，‎ 再根据正弦定理算出AC边和AB边的夹角CAB. ‎ 例2. 某巡逻艇在A处发现北偏东45相距9海里的C处有一艘走私船，正沿南偏东75的方向以10海里/小时的速度向我海岸行驶，巡逻艇立即以14海里/小时的速度沿着直线方向追去，问巡逻艇应该沿什么方向去追？需要多少时间才追赶上该走私船？‎ 19‎ 中山市东升高中 高二数学◆必修5◆导学案 编写：李八江 校审：李志敏 ‎※ 动手试试 练1. 甲、乙两船同时从B点出发，甲船以每小时10(＋1)km的速度向正东航行，乙船以每小时20km的速度沿南60°东的方向航行，1小时后甲、乙两船分别到达A、C两点，求A、C两点的距离，以及在A点观察C点的方向角.‎ 练2. 某渔轮在A处测得在北45°的C处有一鱼群，离渔轮9海里，并发现鱼群正沿南75°东的方向以每小时10海里的速度游去，渔轮立即以每小时14海里的速度沿着直线方向追捕，问渔轮应沿什么方向，需几小时才能追上鱼群？‎ 三、总结提升 ‎※ 学习小结 ‎1. 已知量与未知量全部集中在一个三角形中，依次利用正弦定理或余弦定理解之.；‎ ‎2．已知量与未知量涉及两个或几个三角形，这时需要选择条件足够的三角形优先研究，再逐步在其余的三角形中求出问题的解. ‎ ‎※ 知识拓展 已知ABC的三边长均为有理数，A=，B=，则是有理数，还是无理数？‎ 因为，由余弦定理知 为有理数，‎ 所以为有理数.‎ ‎ 学习评价 ‎ ‎※ 自我评价 你完成本节导学案的情况为（ ）.‎ ‎ A. 很好 B. 较好 C. 一般 D. 较差 ‎※ 当堂检测（时量：5分钟 满分：10分）计分：‎ ‎1. 从A处望B处的仰角为，从B处望A处的俯角为，则，的关系为（ ）.‎ A． B．=‎ C．+= D．+=‎ ‎2. 已知两线段，，若以、为边作三角形，则边所对的角A的取值范围是（ ）.‎ A． B．‎ C． D．‎ ‎3. 关于的方程有相等实根，且A、B、C是的三个内角，则三角形的三边满足（ ）.‎ A． B． ‎ C． D．‎ ‎4. △ABC中，已知a:b:c=(+1) :(-1): ，则此三角形中最大角的度数为 .‎ ‎5. 在三角形中，已知:A，a，b给出下列说法:‎ ‎(1)若A≥90°，且a≤b，则此三角形不存在 ‎ ‎(2)若A≥90°，则此三角形最多有一解 ‎(3)若A＜90°，且a=bsinA，则此三角形为直角三角形，且B=90°‎ ‎(4)当A＜90°，a

查看更多