- 2021-05-06 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
华师版九年级上册数学同步课件-第22章-22 一元二次方程根的判别式
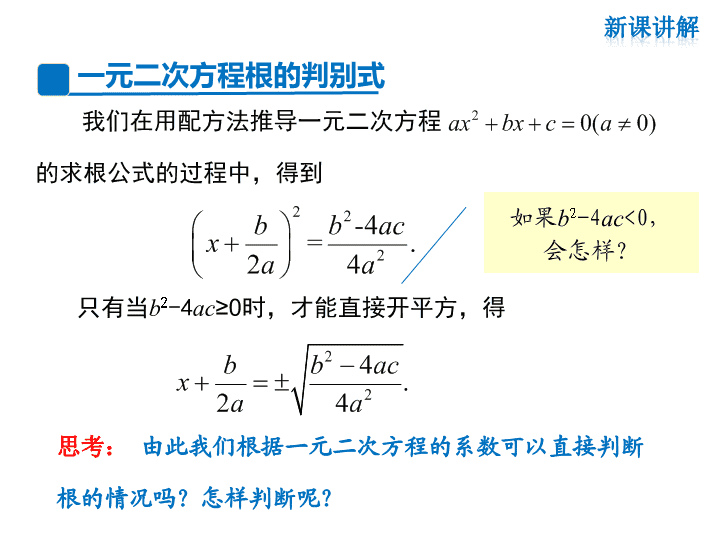
第22章 一元二次方程 22.2 一元二次方程的解法 第4课时 一元二次方程根的判别式 用公式法求下列方程的根: 用公式 法解一元二 次方程的一 般步骤 (1)把方程化为一般形 式,确定a 、b 、c 的值; (3)代入求根公式 计算方程的根 (2)计算 的值 21 2 2 0x x ; 212 1 04 x x ; 23 3 2 3 1 0x x ; 24 1 0.x x 观察与思考 2 2 2 -4= .2 4 b b acx a a 2 2 4 .2 4 b b acx a a 我们在用配方法推导一元二次方程 的求根公式的过程中,得到 2 0( 0)ax bx c a 一元二次方程根的判别式 只有当b2-4ac≥0时,才能直接开平方,得 如果b2-4ac<0, 会怎样? 思考: 由此我们根据一元二次方程的系数可以直接判断 根的情况吗?怎样判断呢? 3.当方程没有实数根时,有 . 1.当方程有两个不相等的实数根时,有 ; 2.当方程有两个相等的实数根时,有 ; 反过来,对于一元二次方程 有: 2 0( 0)ax bx c a 我们把b2-4ac叫做一元二次方程ax2+bx+c=0(a≠0)的根 的判别式,常用符号“∆”来表示,用它可以直接判断一元二 次方程ax2+bx+c=0(a≠0)的实数根的情况: 反之,同样成立 ! 当∆>0 时,方程有两个不相等的实数根; 当∆=0 时,方程有两个相等的实数根; 当∆<0 时,方程没有实数根. 3.判断根的情况,得出结论. 2.计算∆的值,确定∆的符号; ★不解方程,判别一元二次方程的根的情况的一般 步骤 1.将原方程化为一般式,确定 的值;cba 、、 1.不解方程,判别下列方程的根的情况: 2 2 2 1 5 3 2 0 ; 2 2 5 4 2 0 ; 3 2 3 1 0 x x y y x x . 解:(1)因为∆=(-3)2-4×5×(-2)=9+40=49>0, 所以方程有两个不相等的实数根. (2)原方程可变形为25y2-20y+4=0. 因为∆=(-20)2-4×25×4=9=400-400=0, 所以方程有两个相等的实数根. (3)因为∆=( )2-4×2×1=3-8=-5<0, 所以方程没有实数根. 3 2.不解方程,判别关于x的方程 的根的情况. 2 22 2 0x kx k 解: 一元二次方程ax2+bx+c=0(a≠0)的根的情况 反之,同样成立! 当∆>0 时,方程有两个不相等的实数根; 当∆=0 时,方程有两个相等的实数根; 当∆<0 时,方程没有实数根.查看更多