- 2021-05-06 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
一元一次不等式与一次函数(一)导学案1
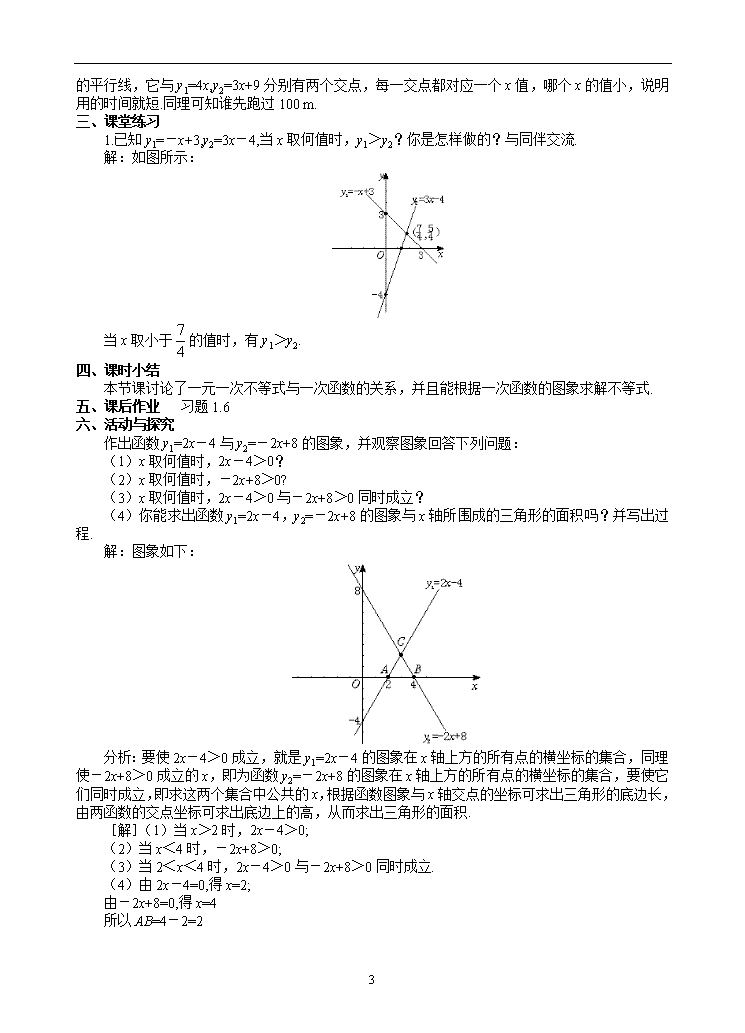
2.5.1 一元一次不等式与一次函数(一) 学习目标 (一)知识认知要求 1.一元一次不等式与一次函数的关系. 2.会根据题意列出函数关系式,画出函数图象,并利用不等关系进行比较. (二)能力训练要求 1.通过一元一次不等式与一次函数的图象之间的结合,培养学生的数形结合意识. 2.训练大家能利用数学知识去解决实际问题的能力. (三)情感与价值观要求 体验数、图形是有效地描述现实世界的重要手段,认识到数学是解决问题和进行交流的重要工具,了解数学对促进社会进步和发展人类理性精神的作用. 学习重点 了解一元一次不等式与一次函数之间的关系. 学习难点 自己根据题意列函数关系式,并能把函数关系式与一元一次不等式联系起来作答. 学习过程 一、创设问题情境,引入新课 上节课我们学习了一元一次不等式的解法,那么,是不是不等式的知识是孤立的呢? .二、新课讲授 1.一元一次不等式与一次函数之间的关系. 大家还记得一次函数吗?请举例给出它的一般形式. 在一次函数y=2x-5中, 当y=0时,有方程2x-5=0; 当y>0时,有不等式2x-5>0; 当y<0时,有不等式2x-5<0. 由此可见,一次函数与一元一次方程、一元一次不等式之间有密切关系,当函数值等于0时即为方程,当函数值大于或小于0时即为不等式. 下面我们来探讨一下一元一次不等式与一次函数的图象之间的关系. 2.做一做 作出函数y=2x-5的图象,观察图象回答下列问题. (1)x取哪些值时,2x-5=0? (2)x取哪些值时,2x-5>0? (3)x取哪些值时,2x-5<0? (4)x取哪些值时,2x-5>3? 请大家讨论后回答: (1)当y=0时,2x-5=0, ∴x=, ∴当x=时,2x-5=0. (2)要找2x-5>0的x的值,也就是函数值y大于0时所对应的x的值,从图象上可知,y>0时,图象在x轴上方,图象上任一点所对应的x值都满足条件,当y=0时,则有2x-5=0,解得 4 x=.当x>时,由y=2x-5可知 y>0.因此当x>时,2x-5>0; (3)同理可知,当x<时,有2x-5<0; (4)要使2x-5>3,也就是y=2x-5中的y大于3,那么过纵坐标为3的点作一条直线平行于x轴,这条直线与y=2x-5相交于一点B(4,3),则当x>4时,有2x-5>3. 3.试一试 如果y=-2x-5,那么当x取何值时,y>0? 由刚才的讨论,大家应该很轻松地完成任务了吧.请大家试一试. 首先要画出函数y=-2x-5的图象,如图: 从图象上可知,图象在x轴上方时,图象上每一点所对应的y的值都大于0,而每一个y的值所对应的x的值都在A点的左侧,即为小于-2.5的数,由-2x-5=0,得x=-2.5,所以当x取小于-2.5的值时,y>0. 4.议一议 兄弟俩赛跑,哥哥先让弟弟跑9 m,然后自己才开始跑,已知弟弟每秒跑3 m,哥哥每秒跑4 m,列出函数关系式,画出函数图象,观察图象回答下列问题: (1)何时弟弟跑在哥哥前面? (2)何时哥哥跑在弟弟前面? (3)谁先跑过20 m?谁先跑过100 m? (4)你是怎样求解的?与同伴交流. 大家应先画出图象,然后讨论回答: [解]设兄弟俩赛跑的时间为x秒.哥哥跑过的路程为y1,弟弟跑过的路程为y2,根据题意,得y1=4x y2=3x+9 函数图象如图: 从图象上来看: (1)当0<x<9时,弟弟跑在哥哥前面; (2)当x>9时,哥哥跑在弟弟前面; (3)弟弟先跑过20m,哥哥先跑过100m; (4)从图象上直接可以观察出(1)、(2)小题,在回答第(3)题时,过y 轴上20这一点作x 4 轴的平行线,它与y1=4x,y2=3x+9分别有两个交点,每一交点都对应一个x值,哪个x的值小,说明用的时间就短.同理可知谁先跑过100 m. 三、课堂练习 1.已知y1=-x+3,y2=3x-4,当x取何值时,y1>y2?你是怎样做的?与同伴交流. 解:如图所示: 当x取小于的值时,有y1>y2. 四、课时小结 本节课讨论了一元一次不等式与一次函数的关系,并且能根据一次函数的图象求解不等式. 五、课后作业 习题1.6 六、活动与探究 作出函数y1=2x-4与y2=-2x+8的图象,并观察图象回答下列问题: (1)x取何值时,2x-4>0? (2)x取何值时,-2x+8>0? (3)x取何值时,2x-4>0与-2x+8>0同时成立? (4)你能求出函数y1=2x-4,y2=-2x+8的图象与x轴所围成的三角形的面积吗?并写出过程. 解:图象如下: 分析:要使2x-4>0成立,就是y1=2x-4的图象在x轴上方的所有点的横坐标的集合,同理使-2x+8>0成立的x,即为函数y2=-2x+8的图象在x轴上方的所有点的横坐标的集合,要使它们同时成立,即求这两个集合中公共的x,根据函数图象与x轴交点的坐标可求出三角形的底边长,由两函数的交点坐标可求出底边上的高,从而求出三角形的面积. [解](1)当x>2时,2x-4>0; (2)当x<4时,-2x+8>0; (3)当2<x<4时,2x-4>0与-2x+8>0同时成立. (4)由2x-4=0,得x=2; 由-2x+8=0,得x=4 所以AB=4-2=2 4 由 得交点C(3,2) 所以三角形ABC中AB边上的高为2. 所以S=×2×2=2. 4查看更多