圆锥曲线导数全国高考数学分类真题含答案

圆锥曲线导数全国高考数学分类真题含答案

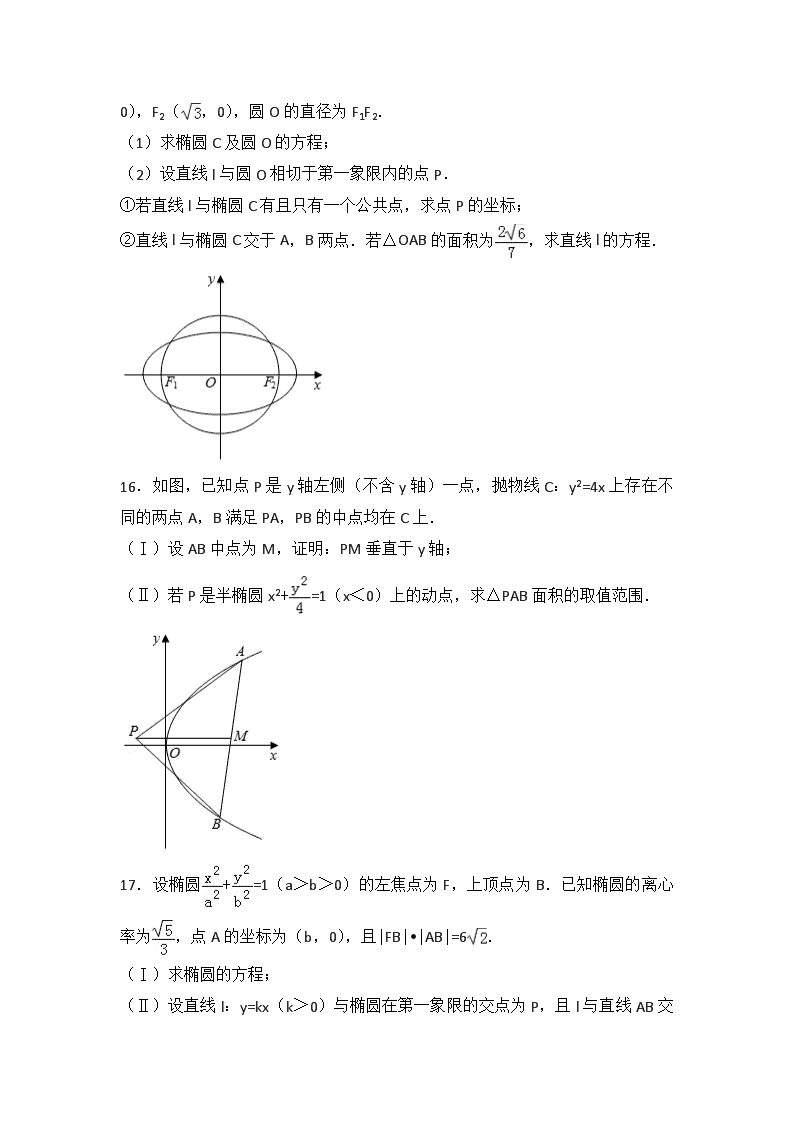
圆锥曲线、导数2018年全国高考数学分类真题（含答案）‎ ‎　‎ 一．选择题（共7小题）‎ ‎1．双曲线﹣y2=1的焦点坐标是（　　）‎ A．（﹣，0），（，0） B．（﹣2，0），（2，0） C．（0，﹣），（0，） D．（0，﹣2），（0，2）‎ ‎2．已知双曲线=1（a＞0，b＞0）的离心率为2，过右焦点且垂直于x轴的直线与双曲线交于A，B两点．设A，B到双曲线的同一条渐近线的距离分别为d1和d2，且d1+d2=6，则双曲线的方程为（　　）‎ A．﹣=1 B．﹣=1 C．﹣=1 D．﹣=1‎ ‎3．设F1，F2是双曲线C：﹣=1（a＞0．b＞0）的左，右焦点，O是坐标原点．过F2作C的一条渐近线的垂线，垂足为P，若|PF1|=|OP|，则C的离心率为（　　）‎ A． B．2 C． D．‎ ‎4．已知F1，F2是椭圆C：=1（a＞b＞0）的左、右焦点，A是C的左顶点，点P在过A且斜率为的直线上，△PF1F2为等腰三角形，∠F1F2P=120°，则C的离心率为（　　）‎ A． B． C． D．‎ ‎5．双曲线=1（a＞0，b＞0）的离心率为，则其渐近线方程为（　　）‎ A．y=±x B．y=±x C．y=±x D．y=±x ‎6．已知双曲线C：﹣y2=1，O为坐标原点，F为C的右焦点，过F的直线与C的两条渐近线的交点分别为M，N．若△OMN为直角三角形，则|MN|=（　　）‎ A． B．3 C．2 D．4‎ ‎7．设函数f（x）=x3+（a﹣1）x2+ax．若f（x）为奇函数，则曲线y=f（x）在点（0，0）处的切线方程为（　　）‎ A．y=﹣2x B．y=﹣x C．y=2x D．y=x ‎　‎ 二．填空题（共6小题）‎ ‎8．在平面直角坐标系xOy中，若双曲线﹣=1（a＞0，b＞0）的右焦点F（c，0）到一条渐近线的距离为c，则其离心率的值为　 　．‎ ‎9．已知椭圆M：+=1（a＞b＞0），双曲线N：﹣=1．若双曲线N的两条渐近线与椭圆M的四个交点及椭圆M的两个焦点恰为一个正六边形的顶点，则椭圆M的离心率为　 　；双曲线N的离心率为　 　．‎ ‎10．已知点P（0，1），椭圆+y2=m（m＞1）上两点A，B满足=2，则当m=　 　时，点B横坐标的绝对值最大．‎ ‎11．已知点M（﹣1，1）和抛物线C：y2=4x，过C的焦点且斜率为k的直线与C交于A，B两点．若∠AMB=90°，则k=‎ ‎　 　．‎ ‎12．曲线y=（ax+1）ex在点（0，1）处的切线的斜率为﹣2，则a=　 　．‎ ‎13．曲线y=2ln（x+1）在点（0，0）处的切线方程为　 　．‎ ‎　‎ 三．解答题（共13小题）‎ ‎14．设函数f（x）=[ax2﹣（4a+1）x+4a+3]ex．‎ ‎（Ⅰ）若曲线y=f（x）在点（1，f（1））处的切线与x轴平行，求a；‎ ‎（Ⅱ）若f（x）在x=2处取得极小值，求a的取值范围．‎ ‎15．如图，在平面直角坐标系xOy中，椭圆C过点（），焦点F1（﹣‎ ‎，0），F2（，0），圆O的直径为F1F2．‎ ‎（1）求椭圆C及圆O的方程；‎ ‎（2）设直线l与圆O相切于第一象限内的点P．‎ ‎①若直线l与椭圆C有且只有一个公共点，求点P的坐标；‎ ‎②直线l与椭圆C交于A，B两点．若△OAB的面积为，求直线l的方程．‎ ‎16．如图，已知点P是y轴左侧（不含y轴）一点，抛物线C：y2=4x上存在不同的两点A，B满足PA，PB的中点均在C上．‎ ‎（Ⅰ）设AB中点为M，证明：PM垂直于y轴；‎ ‎（Ⅱ）若P是半椭圆x2+=1（x＜0）上的动点，求△PAB面积的取值范围．‎ ‎17．设椭圆+=1（a＞b＞0）的左焦点为F，上顶点为B．已知椭圆的离心率为，点A的坐标为（b，0），且|FB|•|AB|=6．‎ ‎（Ⅰ）求椭圆的方程；‎ ‎（Ⅱ）设直线l：y=kx（k＞‎ ‎0）与椭圆在第一象限的交点为P，且l与直线AB交于点Q．若=sin∠AOQ（O为原点），求k的值．‎ ‎18．已知斜率为k的直线l与椭圆C：+=1交于A，B两点，线段AB的中点为M（1，m）（m＞0）．‎ ‎（1）证明：k＜﹣；‎ ‎（2）设F为C的右焦点，P为C上一点，且++=．证明：||，||，||成等差数列，并求该数列的公差．‎ ‎19．设抛物线C：y2=4x的焦点为F，过F且斜率为k（k＞0）的直线l与C交于A，B两点，|AB|=8．‎ ‎（1）求l的方程；‎ ‎（2）求过点A，B且与C的准线相切的圆的方程．‎ ‎20．设椭圆C：+y2=1的右焦点为F，过F的直线l与C交于A，B两点，点M的坐标为（2，0）．‎ ‎（1）当l与x轴垂直时，求直线AM的方程；‎ ‎（2）设O为坐标原点，证明：∠OMA=∠OMB．‎ ‎21．记f′（x），g′（x）分别为函数f（x），g（x）的导函数．若存在x0∈R，满足f（x0）=g（x0）且f′（x0）=g′（x0），则称x0为函数f（x）与g（x）的一个“S点”．‎ ‎（1）证明：函数f（x）=x与g（x）=x2+2x﹣2不存在“S点”；‎ ‎（2）若函数f（x）=ax2﹣1与g（x）=lnx存在“S点”，求实数a的值；‎ ‎（3）已知函数f（x）=﹣x2+a，g（x）=．对任意a＞0，判断是否存在b＞0，使函数f（x）与g（x）在区间（0，+∞）内存在“S点”，并说明理由．‎ ‎22．已知函数f（x）=﹣lnx．‎ ‎（Ⅰ）若f（x）在x=x1，x2（x1≠x2）处导数相等，证明：f（x1）+f（x2）＞8﹣8ln2；‎ ‎（Ⅱ）若a≤3﹣4ln2，证明：对于任意k＞0，直线y=kx+‎ a与曲线y=f（x）有唯一公共点．‎ ‎23．已知函数f（x）=ax，g（x）=logax，其中a＞1．‎ ‎（Ⅰ）求函数h（x）=f（x）﹣xlna的单调区间；‎ ‎（Ⅱ）若曲线y=f（x）在点（x1，f（x1））处的切线与曲线y=g（x）在点（x2，g（x2））处的切线平行，证明x1+g（x2）=；‎ ‎（Ⅲ）证明当a≥e时，存在直线l，使l是曲线y=f（x）的切线，也是曲线y=g（x）的切线．‎ ‎24．已知函数f（x）=（2+x+ax2）ln（1+x）﹣2x．‎ ‎（1）若a=0，证明：当﹣1＜x＜0时，f（x）＜0；当x＞0时，f（x）＞0；‎ ‎（2）若x=0是f（x）的极大值点，求a．‎ ‎25．已知函数f（x）=ex﹣ax2．‎ ‎（1）若a=1，证明：当x≥0时，f（x）≥1；‎ ‎（2）若f（x）在（0，+∞）只有一个零点，求a．‎ ‎26．已知函数f（x）=﹣x+alnx．‎ ‎（1）讨论f（x）的单调性；‎ ‎（2）若f（x）存在两个极值点x1，x2，证明：＜a﹣2．‎ ‎　‎ 圆锥曲线、导数2018年全国高考数学分类真题（含答案）‎ 参考答案与试题解析 ‎　‎ 一．选择题（共7小题）‎ ‎1．双曲线﹣y2=1的焦点坐标是（　　）‎ A．（﹣，0），（，0） B．（﹣2，0），（2，0） C．（0，﹣），（0，） D．（0，﹣2），（0，2）‎ ‎【解答】解：∵双曲线方程可得双曲线的焦点在x轴上，且a2=3，b2=1，‎ 由此可得c==2，‎ ‎∴该双曲线的焦点坐标为（±2，0）‎ 故选：B．‎ ‎　‎ ‎2．已知双曲线=1（a＞0，b＞0）的离心率为2，过右焦点且垂直于x轴的直线与双曲线交于A，B两点．设A，B到双曲线的同一条渐近线的距离分别为d1和d2，且d1+d2=6，则双曲线的方程为（　　）‎ A．﹣=1 B．﹣=1 C．﹣=1 D．﹣=1‎ ‎【解答】解：由题意可得图象如图，CD是双曲线的一条渐近线 y=，即bx﹣ay=0，F（c，0），‎ AC⊥CD，BD⊥CD，FE⊥CD，ACDB是梯形，‎ F是AB的中点，EF==3，‎ EF==b，‎ 所以b=3，双曲线=1（a＞0，b＞0）的离心率为2，可得，‎ 可得：，解得a=．‎ 则双曲线的方程为：﹣=1．‎ 故选：C．‎ ‎　‎ ‎3．设F1，F2是双曲线C：﹣=1（a＞0．b＞0）的左，右焦点，O是坐标原点．过F2作C的一条渐近线的垂线，垂足为P，若|PF1|=|OP|，则C的离心率为（　　）‎ A． B．2 C． D．‎ ‎【解答】解：双曲线C：﹣=1（a＞0．b＞0）的一条渐近线方程为y=x，‎ ‎∴点F2到渐近线的距离d==b，即|PF2|=b，‎ ‎∴|OP|===a，cos∠PF2O=，‎ ‎∵|PF1|=|OP|，‎ ‎∴|PF1|=a，‎ 在三角形F1PF2中，由余弦定理可得|PF1|2=|PF2|2+|F1F2|2﹣2|PF2|•|F1F2|COS∠PF2O，‎ ‎∴6a2=b2+4c2﹣2×b×2c×=4c2﹣3b2=4c2﹣3（c2﹣a2），‎ 即3a2=c2，‎ 即a=c，‎ ‎∴e==，‎ 故选：C．‎ ‎　‎ ‎4．已知F1，F2是椭圆C：=1（a＞b＞0）的左、右焦点，A是C的左顶点，点P在过A且斜率为的直线上，△PF1F2为等腰三角形，∠F1F2P=120°，则C的离心率为（　　）‎ A． B． C． D．‎ ‎【解答】解：由题意可知：A（﹣a，0），F1（﹣c，0），F2（c，0），‎ 直线AP的方程为：y=（x+a），‎ 由∠F1F2P=120°，|PF2|=|F1F2|=2c，则P（2c，c），‎ 代入直线AP：c=（2c+a），整理得：a=4c，‎ ‎∴题意的离心率e==．‎ 故选：D．‎ ‎　‎ ‎5．双曲线=1（a＞0，b＞0）的离心率为，则其渐近线方程为（　　）‎ A．y=±x B．y=±x C．y=±x D．y=±x ‎【解答】解：∵双曲线的离心率为e==，‎ 则=====，‎ 即双曲线的渐近线方程为y=±x=±x，‎ 故选：A．‎ ‎　‎ ‎6．已知双曲线C：﹣y2=1，O为坐标原点，F为C的右焦点，过F的直线与C的两条渐近线的交点分别为M，N．若△OMN为直角三角形，则|MN|=（　　）‎ A． B．3 C．2 D．4‎ ‎【解答】解：双曲线C：﹣y2=1的渐近线方程为：y=，渐近线的夹角为：60°，不妨设过F（2，0）的直线为：y=，‎ 则：解得M（，），‎ 解得：N（），‎ 则|MN|==3．‎ 故选：B．‎ ‎　‎ ‎7．设函数f（x）=x3+（a﹣1）x2+ax．若f（x）为奇函数，则曲线y=f（x）在点（0，0）处的切线方程为（　　）‎ A．y=﹣2x B．y=﹣x C．y=2x D．y=x ‎【解答】解：函数f（x）=x3+（a﹣1）x2+ax，若f（x）为奇函数，‎ 可得a=1，所以函数f（x）=x3+x，可得f′（x）=3x2+1，‎ 曲线y=f（x）在点（0，0）处的切线的斜率为：1，‎ 则曲线y=f（x）在点（0，0）处的切线方程为：y=x．‎ 故选：D．‎ ‎　‎ 二．填空题（共6小题）‎ ‎8．在平面直角坐标系xOy中，若双曲线﹣=1（a＞0，b＞0）的右焦点F（c，0）到一条渐近线的距离为c，则其离心率的值为　2　．‎ ‎【解答】解：双曲线=1（a＞0，b＞0）的右焦点F（c，0）到一条渐近线y=x的距离为c，‎ 可得：=b=，‎ 可得，即c=2a，‎ 所以双曲线的离心率为：e=．‎ 故答案为：2．‎ ‎　‎ ‎9．已知椭圆M：+=1（a＞b＞0），双曲线N：﹣=1．若双曲线N的两条渐近线与椭圆M的四个交点及椭圆M的两个焦点恰为一个正六边形的顶点，则椭圆M的离心率为　　；双曲线N的离心率为　2　．‎ ‎【解答】解：椭圆M：+=1（a＞b＞0），双曲线N：﹣=1．若双曲线N的两条渐近线与椭圆M的四个交点及椭圆M的两个焦点恰为一个正六边形的顶点，‎ 可得椭圆的焦点坐标（c，0），正六边形的一个顶点（，），可得：，可得，可得e4﹣8e2+4=0，e∈（0，1），‎ 解得e=．‎ 同时，双曲线的渐近线的斜率为，即，‎ 可得：，即，‎ 可得双曲线的离心率为e==2．‎ 故答案为：；2．‎ ‎　‎ ‎10．已知点P（0，1），椭圆+y2=m（m＞1）上两点A，B满足=2，则当m=　5　时，点B横坐标的绝对值最大．‎ ‎【解答】解：设A（x1，y1），B（x2，y2），‎ 由P（0，1），=2，‎ 可得﹣x1=2x2，1﹣y1=2（y2﹣1），‎ 即有x1=﹣2x2，y1+2y2=3，‎ 又x12+4y12=4m，‎ 即为x22+y12=m，①‎ x22+4y22=4m，②‎ ‎①﹣②得（y1﹣2y2）（y1+2y2）=﹣3m，‎ 可得y1﹣2y2=﹣m，‎ 解得y1=，y2=，‎ 则m=x22+（）2，‎ 即有x22=m﹣（）2==，‎ 即有m=5时，x22有最大值16，‎ 即点B横坐标的绝对值最大．‎ 故答案为：5．‎ ‎　‎ ‎11．已知点M（﹣1，1）和抛物线C：y2‎ ‎=4x，过C的焦点且斜率为k的直线与C交于A，B两点．若∠AMB=90°，则k=‎ ‎　2　．‎ ‎【解答】解：∵抛物线C：y2=4x的焦点F（1，0），‎ ‎∴过A，B两点的直线方程为y=k（x﹣1），‎ 联立可得，k2x2﹣2（2+k2）x+k2=0，‎ 设A（x1，y1），B（x2，y2），‎ 则 x1+x2=，x1x2=1，‎ ‎∴y1+y2=k（x1+x2﹣2）=，y1y2=k2（x1﹣1）（x2﹣1）=k2[x1x2﹣（x1+x2）+1]=﹣4，‎ ‎∵M（﹣1，1），‎ ‎∴=（x1+1，y1﹣1），=（x2+1，y2﹣1），‎ ‎∵∠AMB=90°=0，∴•=0‎ ‎∴（x1+1）（x2+1）+（y1﹣1）（y2﹣1）=0，‎ 整理可得，x1x2+（x1+x2）+y1y2﹣（y1+y2）+2=0，‎ ‎∴1+2+﹣4﹣+2=0，‎ 即k2﹣4k+4=0，‎ ‎∴k=2．‎ 故答案为：2‎ ‎　‎ ‎12．曲线y=（ax+1）ex在点（0，1）处的切线的斜率为﹣2，则a=　﹣3　．‎ ‎【解答】解：曲线y=（ax+1）ex，可得y′=aex+（ax+1）ex，‎ 曲线y=（ax+1）ex在点（0，1）处的切线的斜率为﹣2，‎ 可得：a+1=﹣2，解得a=﹣3．‎ 故答案为：﹣3．‎ ‎　‎ ‎13．曲线y=2ln（x+1）在点（0，0）处的切线方程为　y=2x　．‎ ‎【解答】解：∵y=2ln（x+1），‎ ‎∴y′=，‎ 当x=0时，y′=2，‎ ‎∴曲线y=2ln（x+1）在点（0，0）处的切线方程为y=2x．‎ 故答案为：y=2x．‎ ‎　‎ 三．解答题（共13小题）‎ ‎14．设函数f（x）=[ax2﹣（4a+1）x+4a+3]ex．‎ ‎（Ⅰ）若曲线y=f（x）在点（1，f（1））处的切线与x轴平行，求a；‎ ‎（Ⅱ）若f（x）在x=2处取得极小值，求a的取值范围．‎ ‎【解答】解：（Ⅰ）函数f（x）=[ax2﹣（4a+1）x+4a+3]ex的导数为 f′（x）=[ax2﹣（2a+1）x+2]ex．‎ 由题意可得曲线y=f（x）在点（1，f（1））处的切线斜率为0，‎ 可得（a﹣2a﹣1+2）e=0，‎ 解得a=1；‎ ‎（Ⅱ）f（x）的导数为f′（x）=[ax2﹣（2a+1）x+2]ex=（x﹣2）（ax﹣1）ex，‎ 若a=0则x＜2时，f′（x）＞0，f（x）递增；x＞2，f′（x）＜0，f（x）递减．‎ x=2处f（x）取得极大值，不符题意；‎ 若a＞0，且a=，则f′（x）=（x﹣2）2ex≥0，f（x）递增，无极值；‎ 若a＞，则＜2，f（x）在（，2）递减；在（2，+∞），（﹣∞，）递增，‎ 可得f（x）在x=2处取得极小值；‎ 若0＜a＜，则＞2，f（x）在（2，）递减；在（，+∞），（﹣∞，2）递增，‎ 可得f（x）在x=2处取得极大值，不符题意；‎ 若a＜0，则＜2，f（x）在（，2）递增；在（2，+∞），（﹣∞，）递减，‎ 可得f（x）在x=2处取得极大值，不符题意．‎ 综上可得，a的范围是（，+∞）．‎ ‎　‎ ‎15．如图，在平面直角坐标系xOy中，椭圆C过点（），焦点F1（﹣，0），F2（，0），圆O的直径为F1F2．‎ ‎（1）求椭圆C及圆O的方程；‎ ‎（2）设直线l与圆O相切于第一象限内的点P．‎ ‎①若直线l与椭圆C有且只有一个公共点，求点P的坐标；‎ ‎②直线l与椭圆C交于A，B两点．若△OAB的面积为，求直线l的方程．‎ ‎【解答】解：（1）由题意可设椭圆方程为，‎ ‎∵焦点F1（﹣，0），F2（，0），∴．‎ ‎∵∴，又a2+b2=c2=3，‎ 解得a=2，b=1．‎ ‎∴椭圆C的方程为：，圆O的方程为：x2+y2=3．‎ ‎（2）①可知直线l与圆O相切，也与椭圆C，且切点在第一象限，‎ ‎∴可设直线l的方程为y=kx+m，（k＜0，m＞0）．‎ 由圆心（0，0）到直线l的距离等于圆半径，可得．‎ 由，可得（4k2+1）x2+8kmx+4m2﹣4=0，‎ ‎△=（8km）2﹣4（4k2+1）（4m2﹣4）=0，‎ 可得m2=4k2+1，∴3k2+3=4k2+1，结合k＜0，m＞0，解得k=﹣，m=3．‎ 将k=﹣，m=3代入可得，‎ 解得x=，y=1，故点P的坐标为（．‎ ‎②设A（x1，y1），B（x2，y2），‎ 由⇒k＜﹣．‎ 联立直线与椭圆方程得（4k2+1）x2+8kmx+4m2﹣4=0，‎ ‎|x2﹣x1|==，‎ O到直线l的距离d=，‎ ‎|AB|=|x2﹣x1|=，‎ ‎△OAB的面积为S===，‎ 解得k=﹣，（正值舍去），m=3．‎ ‎∴y=﹣为所求．‎ ‎　‎ ‎16．如图，已知点P是y轴左侧（不含y轴）一点，抛物线C：y2=4x上存在不同的两点A，B满足PA，PB的中点均在C上．‎ ‎（Ⅰ）设AB中点为M，证明：PM垂直于y轴；‎ ‎（Ⅱ）若P是半椭圆x2+=1（x＜0）上的动点，求△PAB面积的取值范围．‎ ‎【解答】解：（Ⅰ）证明：可设P（m，n），A（，y1），B（，y2），‎ AB中点为M的坐标为（，），‎ 抛物线C：y2=4x上存在不同的两点A，B满足PA，PB的中点均在C上，‎ 可得（）2=4•，‎ ‎（）2=4•，‎ 化简可得y1，y2为关于y的方程y2﹣2ny+8m﹣n2=0的两根，‎ 可得y1+y2=2n，y1y2=8m﹣n2，‎ 可得n=，‎ 则PM垂直于y轴；‎ ‎（Ⅱ）若P是半椭圆x2+=1（x＜0）上的动点，‎ 可得m2+=1，﹣1≤m＜0，﹣2＜n＜2，‎ 由（Ⅰ）可得y1+y2=2n，y1y2=8m﹣n2，‎ 由PM垂直于y轴，可得△PAB面积为S=|PM|•|y1﹣y2|‎ ‎=（﹣m）•‎ ‎=[•（4n2﹣16m+2n2）﹣m]•‎ ‎=（n2﹣4m），‎ 可令t==‎ ‎=，‎ 可得m=﹣时，t取得最大值；‎ m=﹣1时，t取得最小值2，‎ 即2≤t≤，‎ 则S=t3在2≤t≤递增，可得S∈[6，]，‎ ‎△PAB面积的取值范围为[6，]．‎ ‎　‎ ‎17．设椭圆+=1（a＞b＞0）的左焦点为F，上顶点为B．已知椭圆的离心率为，点A的坐标为（b，0），且|FB|•|AB|=6．‎ ‎（Ⅰ）求椭圆的方程；‎ ‎（Ⅱ）设直线l：y=kx（k＞‎ ‎0）与椭圆在第一象限的交点为P，且l与直线AB交于点Q．若=sin∠AOQ（O为原点），求k的值．‎ ‎【解答】解：（Ⅰ）设椭圆+=1（a＞b＞0）的焦距为2c，‎ 由椭圆的离心率为e=，‎ ‎∴=；‎ 又a2=b2+c2，‎ ‎∴2a=3b，‎ 由|FB|=a，|AB|=b，且|FB|•|AB|=6；‎ 可得ab=6，‎ 从而解得a=3，b=2，‎ ‎∴椭圆的方程为+=1；‎ ‎（Ⅱ）设点P的坐标为（x1，y1），点Q的坐标为（x2，y2），由已知y1＞y2＞0；‎ ‎∴|PQ|sin∠AOQ=y1﹣y2；‎ 又|AQ|=，且∠OAB=，‎ ‎∴|AQ|=y，‎ 由=sin∠AOQ，可得5y1=9y2；‎ 由方程组，消去x，可得y1=，‎ ‎∴直线AB的方程为x+y﹣2=0；‎ 由方程组，消去x，可得y2=；‎ 由5y1=9y2，可得5（k+1）=3，‎ 两边平方，整理得56k2﹣50k+11=0，‎ 解得k=或k=；‎ ‎∴k的值为或．‎ ‎　‎ ‎18．已知斜率为k的直线l与椭圆C：+=1交于A，B两点，线段AB的中点为M（1，m）（m＞0）．‎ ‎（1）证明：k＜﹣；‎ ‎（2）设F为C的右焦点，P为C上一点，且++=．证明：||，||，||成等差数列，并求该数列的公差．‎ ‎【解答】解：（1）设A（x1，y1），B（x2，y2），‎ ‎∵线段AB的中点为M（1，m），‎ ‎∴x1+x2=2，y1+y2=2m 将A，B代入椭圆C：+=1中，可得 ‎，‎ 两式相减可得，3（x1+x2）（x1﹣x2）+4（y1+y2）（y1﹣y2）=0，‎ 即6（x1﹣x2）+8m（y1﹣y2）=0，‎ ‎∴k==﹣=﹣‎ 点M（1，m）在椭圆内，即，‎ 解得0＜m ‎∴．‎ ‎（2）证明：设A（x1，y1），B（x2，y2），P（x3，y3），‎ 可得x1+x2=2，‎ ‎∵++=，F（1，0），∴x1﹣1+x2﹣1+x3﹣1=0，y1+y2+y3=0，‎ ‎∴x3=1，‎ ‎∵m＞0，可得P在第一象限，故，m=，k=﹣1‎ 由椭圆的焦半径公式得则|FA|=a﹣ex1=2﹣x1，|FB|=2﹣x2，|FP|=2﹣x3=．‎ 则|FA|+|FB|=4﹣，∴|FA|+|FB|=2|FP|，‎ 联立，可得|x1﹣x2|=‎ 所以该数列的公差d满足2d=|x1﹣x2|=，‎ ‎∴该数列的公差为±．‎ ‎　‎ ‎19．设抛物线C：y2=4x的焦点为F，过F且斜率为k（k＞0）的直线l与C交于A，B两点，|AB|=8．‎ ‎（1）求l的方程；‎ ‎（2）求过点A，B且与C的准线相切的圆的方程．‎ ‎【解答】解：（1）方法一：抛物线C：y2=4x的焦点为F（1，0），当直线的斜率不存在时，|AB|=4，不满足；‎ 设直线AB的方程为：y=k（x﹣1），设A（x1，y1），B（x2，y2），‎ 则，整理得：k2x2﹣2（k2+2）x+k2=0，则x1+x2=，x1x2=1，‎ 由|AB|=x1+x2+p=+2=8，解得：k2=1，则k=1，‎ ‎∴直线l的方程y=x﹣1；‎ 方法二：抛物线C：y2=4x的焦点为F（1，0），设直线AB的倾斜角为θ，由抛物线的弦长公式|AB|===8，解得：sin2θ=，‎ ‎∴θ=，则直线的斜率k=1，‎ ‎∴直线l的方程y=x﹣1；‎ ‎（2）过A，B分别向准线x=﹣1作垂线，垂足分别为A1，B1，设AB的中点为D，过D作DD1⊥准线l，垂足为D，则|DD1|=（|AA1|+|BB1|）‎ 由抛物线的定义可知：|AA1|=|AF|，|BB1|=|BF|，则r=|DD1|=4，‎ 以AB为直径的圆与x=﹣1相切，且该圆的圆心为AB的中点D，‎ 由（1）可知：x1+x2=6，y1+y2=x1+x2﹣2=4，‎ 则D（3，2），‎ 过点A，B且与C的准线相切的圆的方程（x﹣3）2+（y﹣2）2=16．．‎ ‎　‎ ‎20．设椭圆C：+y2=1的右焦点为F，过F的直线l与C交于A，B两点，点M的坐标为（2，0）．‎ ‎（1）当l与x轴垂直时，求直线AM的方程；‎ ‎（2）设O为坐标原点，证明：∠OMA=∠OMB．‎ ‎【解答】解：（1）c==1，‎ ‎∴F（1，0），‎ ‎∵l与x轴垂直，‎ ‎∴x=1，‎ 由，解得或，‎ ‎∴A（1.），或（1，﹣），‎ ‎∴直线AM的方程为y=﹣x+，y=x﹣，‎ 证明：（2）当l与x轴重合时，∠OMA=∠OMB=0°，‎ 当l与x轴垂直时，OM为AB的垂直平分线，∴∠OMA=∠OMB，‎ 当l与x轴不重合也不垂直时，设l的方程为y=k（x﹣1），k≠0，‎ A（x1，y1），B（x2，y2），则x1＜，x2＜，‎ 直线MA，MB的斜率之和为kMA，kMB之和为kMA+kMB=+，‎ 由y1=kx1﹣k，y2=kx2﹣k得kMA+kMB=，‎ 将y=k（x﹣1）代入+y2=1可得（2k2+1）x2﹣4k2x+2k2﹣2=0，‎ ‎∴x1+x2=，x1x2=，‎ ‎∴2kx1x2﹣3k（x1+x2）+4k=（4k2﹣4k﹣12k2+8k2+4k）=0‎ 从而kMA+kMB=0，‎ 故MA，MB的倾斜角互补，‎ ‎∴∠OMA=∠OMB，‎ 综上∠OMA=∠OMB．‎ ‎　‎ ‎21．记f′（x），g′（x）分别为函数f（x），g（x）的导函数．若存在x0∈R，满足f（x0）=g（x0）且f′（x0）=g′（x0），则称x0为函数f（x）与g（x）的一个“S点”．‎ ‎（1）证明：函数f（x）=x与g（x）=x2+2x﹣2不存在“S点”；‎ ‎（2）若函数f（x）=ax2﹣1与g（x）=lnx存在“S点”，求实数a的值；‎ ‎（3）已知函数f（x）=﹣x2+a，g（x）=．对任意a＞0，判断是否存在b＞0，使函数f（x）与g（x）在区间（0，+∞）内存在“S点”，并说明理由．‎ ‎【解答】解：（1）证明：f′（x）=1，g′（x）=2x+2，‎ 则由定义得，得方程无解，则f（x）=x与g（x）=x2+2x﹣2不存在“S点”；‎ ‎（2）f′（x）=2ax，g′（x）=，x＞0，‎ 由f′（x）=g′（x）得=2ax，得x=，‎ f（）=﹣=g（）=﹣lna2，得a=；‎ ‎（3）f′（x）=﹣2x，g′（x）=，（x≠0），‎ 由f′（x0）=g′（x0），得b=﹣＞0，得0＜x0＜1，‎ 由f（x0）=g（x0），得﹣x02+a==﹣，得a=x02﹣，‎ 令h（x）=x2﹣﹣a=，（a＞0，0＜x＜1），‎ 设m（x）=﹣x3+3x2+ax﹣a，（a＞0，0＜x＜1），‎ 则m（0）=﹣a＜0，m（1）=2＞0，得m（0）m（1）＜0，‎ 又m（x）的图象在（0，1）上连续不断，‎ 则m（x）在（0，1）上有零点，‎ 则h（x）在（0，1）上有零点，‎ 则f（x）与g（x）在区间（0，+∞）内存在“S”点．‎ ‎　‎ ‎22．已知函数f（x）=﹣lnx．‎ ‎（Ⅰ）若f（x）在x=x1，x2（x1≠x2）处导数相等，证明：f（x1）+f（x2）＞8﹣8ln2；‎ ‎（Ⅱ）若a≤3﹣4ln2，证明：对于任意k＞0，直线y=kx+a与曲线y=f（x）有唯一公共点．‎ ‎【解答】证明：（Ⅰ）∵函数f（x）=﹣lnx，‎ ‎∴x＞0，f′（x）=﹣，‎ ‎∵f（x）在x=x1，x2（x1≠x2）处导数相等，‎ ‎∴=﹣，‎ ‎∵x1≠x2，∴+=，‎ 由基本不等式得：=≥，‎ ‎∵x1≠x2，∴x1x2＞256，‎ 由题意得f（x1）+f（x2）==﹣ln（x1x2），‎ 设g（x）=，则，‎ ‎∴列表讨论：‎ ‎ x ‎ （0，16）‎ ‎ 16‎ ‎ （16，+∞）‎ ‎ g′（x）‎ ‎﹣‎ ‎ 0‎ ‎+‎ ‎ g（x）‎ ‎↓‎ ‎ 2﹣4ln2‎ ‎↑‎ ‎∴g（x）在[256，+∞）上单调递增，‎ ‎∴g（x1x2）＞g（256）=8﹣8ln2，‎ ‎∴f（x1）+f（x2）＞8﹣8ln2．‎ ‎（Ⅱ）令m=e﹣（|a|+k），n=（）2+1，‎ 则f（m）﹣km﹣a＞|a|+k﹣k﹣a≥0，‎ f（n）﹣kn﹣a＜n（﹣﹣k）≤n（﹣k）＜0，‎ ‎∴存在x0∈（m，n），使f（x0）=kx0+a，‎ ‎∴对于任意的a∈R及k∈（0，+∞），直线y=kx+a与曲线y=f（x）有公共点，‎ 由f（x）=kx+a，得k=，‎ 设h（x）=，则h′（x）==，‎ 其中g（x）=﹣lnx，‎ 由（1）知g（x）≥g（16），‎ 又a≤3﹣4ln2，∴﹣g（x）﹣1+a≤﹣g（16）﹣1+a=﹣3+4ln2+a≤0，‎ ‎∴h′（x）≤0，即函数h（x）在（0，+∞）上单调递减，‎ ‎∴方程f（x）﹣kx﹣a=0至多有一个实根，‎ 综上，a≤3﹣4ln2时，对于任意k＞0，直线y=kx+a与曲线y=f（x）有唯一公共点．‎ ‎　‎ ‎23．已知函数f（x）=ax，g（x）=logax，其中a＞1．‎ ‎（Ⅰ）求函数h（x）=f（x）﹣xlna的单调区间；‎ ‎（Ⅱ）若曲线y=f（x）在点（x1，f（x1））处的切线与曲线y=g（x）在点（x2，g（x2））处的切线平行，证明x1+g（x2）=；‎ ‎（Ⅲ）证明当a≥e时，存在直线l，使l是曲线y=f（x）的切线，也是曲线y=g（x）的切线．‎ ‎【解答】（Ⅰ）解：由已知，h（x）=ax﹣xlna，有h′（x）=axlna﹣lna，‎ 令h′（x）=0，解得x=0．‎ 由a＞1，可知当x变化时，h′（x），h（x）的变化情况如下表：‎ ‎ x ‎ （﹣∞，0）‎ ‎ 0‎ ‎ （0，+∞）‎ ‎ h′（x）‎ ‎﹣‎ ‎ 0‎ ‎+‎ ‎ h（x）‎ ‎↓‎ ‎ 极小值 ‎↑‎ ‎∴函数h（x）的单调减区间为（﹣∞，0），单调递增区间为（0，+∞）；‎ ‎（Ⅱ）证明：由f′（x）=axlna，可得曲线y=f（x）在点（x1，f（x1‎ ‎））处的切线的斜率为lna．‎ 由g′（x）=，可得曲线y=g（x）在点（x2，g（x2））处的切线的斜率为．‎ ‎∵这两条切线平行，故有，即，‎ 两边取以a为底数的对数，得logax2+x1+2logalna=0，‎ ‎∴x1+g（x2）=；‎ ‎（Ⅲ）证明：曲线y=f（x）在点（）处的切线l1：，‎ 曲线y=g（x）在点（x2，logax2）处的切线l2：．‎ 要证明当a≥时，存在直线l，使l是曲线y=f（x）的切线，也是曲线y=g（x）的切线，‎ 只需证明当a≥时，存在x1∈（﹣∞，+∞），x2∈（0，+∞）使得l1与l2重合，‎ 即只需证明当a≥时，方程组 由①得，代入②得：‎ ‎，③‎ 因此，只需证明当a≥时，关于x1 的方程③存在实数解．‎ 设函数u（x）=，既要证明当a≥时，函数y=u（x）存在零点．‎ u′（x）=1﹣（lna）2xax，可知x∈（﹣∞，0）时，u′（x）＞0；x∈（0，+∞）时，u′（x）单调递减，‎ 又u′（0）=1＞0，u′=＜0，‎ 故存在唯一的x0，且x0＞0，使得u′（x0）=0，即．‎ 由此可得，u（x）在（﹣∞，x0）上单调递增，在（x0，+∞）上单调递减，‎ u（x）在x=x0处取得极大值u（x0）．‎ ‎∵，故lnlna≥﹣1．‎ ‎∴=．‎ 下面证明存在实数t，使得u（t）＜0，‎ 由（Ⅰ）可得ax≥1+xlna，当时，有 u（x）≤=．‎ ‎∴存在实数t，使得u（t）＜0．‎ 因此，当a≥时，存在x1∈（﹣∞，+∞），使得u（x1）=0．‎ ‎∴当a≥时，存在直线l，使l是曲线y=f（x）的切线，也是曲线y=g（x）的切线．‎ ‎　‎ ‎24．已知函数f（x）=（2+x+ax2）ln（1+x）﹣2x．‎ ‎（1）若a=0，证明：当﹣1＜x＜0时，f（x）＜0；当x＞0时，f（x）＞0；‎ ‎（2）若x=0是f（x）的极大值点，求a．‎ ‎【解答】（1）证明：当a=0时，f（x）=（2+x）ln（1+x）﹣2x，（x＞﹣1）．‎ ‎，，‎ 可得x∈（﹣1，0）时，f″（x）≤0，x∈（0，+∞）时，f″（x）≥0‎ ‎∴f′（x）在（﹣1，0）递减，在（0，+∞）递增，‎ ‎∴f′（x）≥f′（0）=0，‎ ‎∴f（x）=（2+x）ln（1+x）﹣2x在（﹣1，+∞）上单调递增，又f（0）=0．‎ ‎∴当﹣1＜x＜0时，f（x）＜0；当x＞0时，f（x）＞0．‎ ‎（2）解：由f（x）=（2+x+ax2）ln（1+x）﹣2x，得 f′（x）=（1+2ax）ln（1+x）+﹣2=，‎ 令h（x）=ax2﹣x+（1+2ax）（1+x）ln（x+1），‎ h′（x）=4ax+（4ax+2a+1）ln（x+1）．‎ 当a≥0，x＞0时，h′（x）＞0，h（x）单调递增，‎ ‎∴h（x）＞h（0）=0，即f′（x）＞0，‎ ‎∴f（x）在（0，+∞）上单调递增，故x=0不是f（x）的极大值点，不符合题意．‎ 当a＜0时，h″（x）=8a+4aln（x+1）+，‎ 显然h″（x）单调递减，‎ ‎①令h″（0）=0，解得a=﹣．‎ ‎∴当﹣1＜x＜0时，h″（x）＞0，当x＞0时，h″（x）＜0，‎ ‎∴h′（x）在（﹣1，0）上单调递增，在（0，+∞）上单调递减，‎ ‎∴h′（x）≤h′（0）=0，‎ ‎∴h（x）单调递减，又h（0）=0，‎ ‎∴当﹣1＜x＜0时，h（x）＞0，即f′（x）＞0，‎ 当x＞0时，h（x）＜0，即f′（x）＜0，‎ ‎∴f（x）在（﹣1，0）上单调递增，在（0，+∞）上单调递减，‎ ‎∴x=0是f（x）的极大值点，符合题意；‎ ‎②若﹣＜a＜0，则h″（0）=1+6a＞0，h″（e﹣1）=（2a﹣1）（1﹣e）＜0，‎ ‎∴h″（x）=0在（0，+∞）上有唯一一个零点，设为x0，‎ ‎∴当0＜x＜x0时，h″（x）＞0，h′（x）单调递增，‎ ‎∴h′（x）＞h′（0）=0，即f′（x）＞0，‎ ‎∴f（x）在（0，x0）上单调递增，不符合题意；‎ ‎③若a＜﹣，则h″（0）=1+6a＜0，h″（﹣1）=（1﹣2a）e2＞0，‎ ‎∴h″（x）=0在（﹣1，0）上有唯一一个零点，设为x1，‎ ‎∴当x1＜x＜0时，h″（x）＜0，h′（x）单调递减，‎ ‎∴h′（x）＞h′（0）=0，∴h（x）单调递增，‎ ‎∴h（x）＜h（0）=0，即f′（x）＜0，‎ ‎∴f（x）在（x1，0）上单调递减，不符合题意．‎ 综上，a=﹣．‎ ‎　‎ ‎25．已知函数f（x）=ex﹣ax2．‎ ‎（1）若a=1，证明：当x≥0时，f（x）≥1；‎ ‎（2）若f（x）在（0，+∞）只有一个零点，求a．‎ ‎【解答】证明：（1）当a=1时，函数f（x）=ex﹣x2．‎ 则f′（x）=ex﹣2x，‎ 令g（x）=ex﹣2x，则g′（x）=ex﹣2，‎ 令g′（x）=0，得x=ln2．‎ 当x∈（0，ln2）时，g′（x）＜0，当x∈（ln2，+∞）时，g′（x）＞0，‎ ‎∴g（x）≥g（ln2）=eln2﹣2•ln2=2﹣2ln2＞0，‎ ‎∴f（x）在[0，+∞）单调递增，∴f（x）≥f（0）=1，‎ 解：（2），f（x）在（0，+∞）只有一个零点⇔方程ex﹣ax2=0在（0，+∞）只有一个根，‎ ‎⇔a=在（0，+∞）只有一个根，‎ 即函数y=a与G（x）=的图象在（0，+∞）只有一个交点．‎ G，‎ 当x∈（0，2）时，G′（x）＜0，当∈（2，+∞）时，G′（x）＞0，‎ ‎∴G（x）在（0，2）递减，在（2，+∞）递增，‎ 当→0时，G（x）→+∞，当→+∞时，G（x）→+∞，‎ ‎∴f（x）在（0，+∞）只有一个零点时，a=G（2）=．‎ ‎　‎ ‎26．已知函数f（x）=﹣x+alnx．‎ ‎（1）讨论f（x）的单调性；‎ ‎（2）若f（x）存在两个极值点x1，x2，证明：＜a﹣2．‎ ‎【解答】解：（1）函数的定义域为（0，+∞），‎ 函数的导数f′（x）=﹣﹣1+=﹣，‎ 设g（x）=x2﹣ax+1，‎ 当a≤0时，g（x）＞0恒成立，即f′（x）＜0恒成立，此时函数f（x）在（0，+∞）上是减函数，‎ 当a＞0时，判别式△=a2﹣4，‎ ‎①当0＜a≤2时，△≤0，即g（x）＞0，即f′（x）＜0恒成立，此时函数f（x）在（0，+∞）上是减函数，‎ ‎②当a＞2时，x，f′（x），f（x）的变化如下表：‎ ‎ x ‎ （0，）‎ ‎ ‎ ‎ （，）‎ ‎ ‎ ‎ （，+∞）‎ ‎ f′（x）‎ ‎﹣‎ ‎ 0‎ ‎+‎ ‎ 0‎ ‎﹣‎ ‎ f（x）‎ ‎ 递减 ‎ 递增 递减 综上当a≤2时，f（x）在（0，+∞）上是减函数，‎ 当a＞2时，在（0，），和（，+∞）上是减函数，‎ 则（，）上是增函数．‎ ‎（2）由（1）知a＞2，0＜x1＜1＜x2，x1x2=1，‎ 则f（x1）﹣f（x2）=（x2﹣x1）（1+）+a（lnx1﹣lnx2）=2（x2﹣x1）+a（lnx1﹣lnx2），‎ 则=﹣2+，‎ 则问题转为证明＜1即可，‎ 即证明lnx1﹣lnx2＞x1﹣x2，‎ 即证2lnx1＞x1﹣在（0，1）上恒成立，‎ 设h（x）=2lnx﹣x+，（0＜x＜1），其中h（1）=0，‎ 求导得h′（x）=﹣1﹣=﹣=﹣＜0，‎ 则h（x）在（0，1）上单调递减，‎ ‎∴h（x）＞h（1），即2lnx﹣x+＞0，‎ 故2lnx＞x﹣，‎ 则＜a﹣2成立．‎ ‎　‎