七年级下册数学课件《平移》 人教新课标 (8)

七年级下册数学课件《平移》 人教新课标 (8)

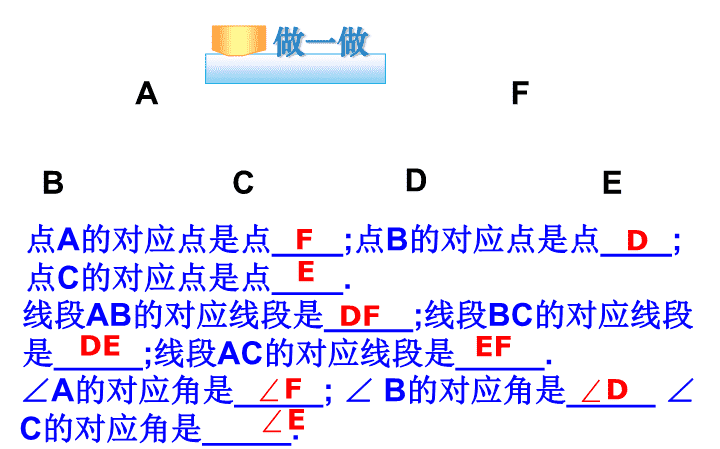
10.2平移 在平面内，将一个图形沿着某个方向移动一定 的距 离，这样的图形运动叫做图形的平移。 平移不改变图形的形状、大小，只改变图形的位 置。它由移动的方向和距离决定 A B C D A` B` C` D` A B C F D E 点A的对应点是点____;点B的对应点是点____; 点C的对应点是点____. 线段AB的对应线段是_____;线段BC的对应线段 是_____;线段AC的对应线段是_____. ∠A的对应角是_____; ∠ B的对应角是_____ ∠ C的对应角是_____. F D E DF EF ∠F ∠D ∠E DE 图中的4个小三角形都是等边三角形，边长 为1.3cm。你能通过平移∆ABC得到其他三角形 吗？若能，请画出平移的方向，并说出平移的 距离。 D A B F E C 动手做做：用三角板、直尺画平行线。 P Q D E F A B C 观察：线段AB与DE的位置关系与数量关系，∠B与 ∠E的关系呢？ 直尺PQ是倾斜放置，用三角 板能否画 出平行线？ AB//CD AB=CD ∠B=∠E 观察：线段AC与DF的位置关系与数量关系，∠A与 ∠D的关系呢？ AC//DF AC=DF ∠A=∠D 注意:在平移过程中,对应 线段也可能在一条直线上 (如:BC与EF) 平移后的图形与原来的图形的对应线段 平行且相等，对应角相等； 平移的方向是直尺PQ倾斜放置的方向， 平移的距离是BE的长度。 在平移过程中，对应线段也可能在一条 直线上，如BC与EF； 平移后图形的形状与大小都没有变化； P Q A B C A’ B’ C’ 观察右图， △ABC沿着PQ的 方向平移到△A‘B’C‘ 的位置，除了对应线 段平行并且相等外， 你还发现有哪些线段 平行且相等？ AA’∥BB’∥CC’ AA’=BB’=CC’ 即：平移后对应点所连的线段平行且相等。 这是平移的特征 之一 M M’ 注意:在平移过程中， 对应点所连的线段也 可能在一条直线上。 A B C A’ B’ C’ BC的中点M平移到 什么地方却了？ P Q R S B C A A’ B’ C’ A” B” C” 将图中的 A’B’C’沿RS方向平移到 A”B”C”的位置，其平移的距离是 线段RS的长度。   （课本68页） (1)对应线段平行（或在一条直线上）且相等，对应角相等； (2)平移后对应点所连的线段平行（或在一条直线上）且相 等； (3)图形上所有的点都作了相同的平移（即相同的平移方向 和相同的平移距离），并且平移后图形的形状和大小都不 变. 作图方法：把握平移的方向和平移的距离、 画出原图形中的关键 点的对应点，连接即可。 总结平移的特征 Ａ B C D 　如图，将△ABC 的顶点A移动到点 D处，作出平移后 的△DEF。 你是怎么作的？请说说你的方法。 Ａ B C D 1、将点D向下移动3 格找到B点的对应点E。 E F 　2、E向右移动3格可 以找到C点的对应点F。 3、连结线段即可。 你还有不同的方法吗？ Ａ B C D 　　观察出点D是点A 向右移动5格，再向上 移动4格得到的，所以 按照同样的方法可以 得到点B和点C的对应 点，然后再连结线段 即可。 E F 你还有不同的方法吗？ Ａ B C D 先连结AD，再 分别过B、C两点作 与AD的平行且相 等的线段，找出B 点和C点的对应点。E F 　对比三种方法，你觉 得那种方法更实用啊？ 方法三是基本法，大家要注意。 如图，任意△ABC 的顶点A移动到点 D处，作出平移后 的△DEF。 Ａ B C D E F 1、把握原图形中的关键点，画出对应点 2、把握平移的方向和平移的距离 使得 AD∥BE//CF， AD=BE=CF 画出字母K沿着线段MN的方向平移后的位 置,平移的距离是线段MN的长度； NM 2cm 将所给图形沿着线段PQ的方向平移,平移的距离是 线段PQ的长度，画出平移后的新图形. 解 如下图所示： 要正确画出一个图形按要求平移后的新图形，只要先画出关键 点的对应点，如线段的端点、三角形的顶点、圆的圆心等等， 就很容易画出新图形了 思考题：你能运用今天所学的平移知识 将△ABC平移使点A 移动到A1，画出平 移后的三角形。 A CB A′ B1 C1 例 如图：ΔA’B’C’是由ΔABC沿射线BB’ 的方向移动5cm得到的. BC与B’C’在一条 直线上. 若BC=3cm, 则B’C=? A B C C'B' A' 练习1 如图：ΔDEF可以看作ΔABC平移得到 1）平移的方向是 ；平移的距离是 . 2）AB∥ ； ∥ . 3）若BC=5cm，CF=3cm， 则BE= cm，CE= cm，EF= cm. 4）若连结AD，与AD相等的线段 是： . A B C FE D 若∠A=60o，将∠A先向左平移1cm，再向 下平移2cm，则∠A的大小（ ） A、变小 B、变大 C、不变 D、无法确定 练习2 将线段AB=2cm，向右平移3cm后得到线段 CD，则线段CD= cm，BD= cm. 练习3 B A D C A B DC 如图，在ΔABC中，∠A=40o，∠C=35o， 将ΔABC平移得到ΔDEF，DF与BC交于 点G， 你能求出∠DGB与∠E的度数吗？ G D E F CB A 练习4 如图：在梯形ABCD中，AD∥BC， ∠B+∠C=90o，点E在AD上，先将AB向右平移， 使点A与点E重合，交BC于F，再将DC向左平移， 使点D与点E重合，交BC于G，请判断ΔEFG的 形状. GFB C A DE “若AD=3，FG=5，求BC的长” 练习5 已知梯形ABCD中，AD∥BC， AB=DC=3cm，AD=2cm，∠C=60o ， 求线段BC的长 A B C D E 练习6 A B C A B  C  如图所示，ABC 经过平移到 ABC   的位置，指出平移 （1）先找到对应点； （2）连结两个对应点； （3）由一个点平移到另一个点的移动方向，就是图形 移动的方向.所以平移的方向就是点A到点 的方向A （4）平移的距离就是线段 AA的长度，约为2.4厘米。 的方向，并量出平移的距离。 A B C A B C  A B C  A B C   可以看成是 ABC 经过一次平移而得到的图形， 它的平移方向是由对应点A到对应点A的方向，他的平移 距离是线段AA的长度，经过测量可得约为2.6cm。 课堂小结 1、在平面内，一个图形经过平移后得到的图形与原来图形的对应 线段平行（或在同一条直线上）且相等，对应角相等， 3、平移前后，图形的大小、形状没有改变，只是位置发生了变化。 2、对应点所连接的线段平行（或在同一条直线上）且相等。