七年级下册数学课件《坐标方法的简单应用》 人教新课标 (4)

七年级下册数学课件《坐标方法的简单应用》 人教新课标 (4)

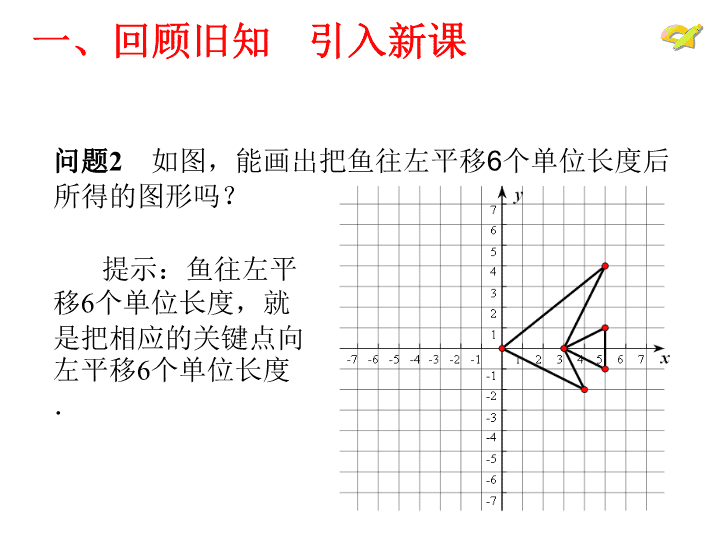
7.2.2坐标方法的简单应用 问题1　什么叫做平移？平移后得到的新图形与 原图形有什么关系？ 一、回顾旧知 引入新课 把一个图形整体沿某一方向移动一定的距 离，图形的这种移动，叫做平移；平移后图形 的位置改变，形状、大小不变． 问题2　如图，能画出把鱼往左平移6个单位长度后 所得的图形吗？ 提示：鱼往左平 移6个单位长度，就 是把相应的关键点向 左平移6个单位长 度． 一、回顾旧知 引入新课 想一想 图形平移，图形的大小不变，但位置 发生了变化，那图形上点的坐标也随着发 生了怎样的变化呢？ 一、回顾旧知 引入新课 问题3　 （1）如图2，将点A （－2，－3）向右平移 5个单位长度，得到点 A1，在图上标出它的坐 标，观察坐标的变化， 你能从中发现什么规律 吗？把点A向上平移4个 单位长度呢？ 二、探究发现 合作交流 问题3 （2）把点A向左或向下 平移4个单位长度，观察 坐标的变化，你能从中 发现什么规律吗？ （3）再找几个点，对它 们进行平移，观察它们 的坐标是否按你发现的 规律变化？ 二、探究发现 合作交流 点A（-2，-3）向右平移5个单位长度， 得到点A1，它的坐标是（3，-3）．观察点A， 点A1的坐标可以发现：点A1的横坐标等于点A 的横坐标加5， 点A1的纵坐标等于点A的纵坐 标．类似地，将点A向上或向左或向下平移 某个单位长度，找出平移后得到的点的坐标 与点A的坐标的关系．然后再找几个点，对 它们进行平移，发现前面的变化规律仍然成 立． 二、探究发现 合作交流 说说点或图形的平移引起点的坐标的变化规律？ 在平面直角坐标系中，将点（x，y）向右 （或左）平移a个单位长度，可以得到对应点的 坐标是（x+a ，y） 或（x-a ，y） ；将点（x，y） 向上（或下）平移b个单位长度，可以得到对应 点的坐标是（x，y+b）或（x，y-b）． 探究发现 合作交流 问题4　如图，如何沿坐标轴方向平移A（-2，1） 得到A1？ 点A先向右平移5 个单位长度，再向 下平移3个单位长 度；或将点A先向 下平移3个单位长 度，再向右平移5 个单位长度． 三、巩固应用 拓展延伸 问题5　如图4，正方形ABCD四个顶点的坐标分别是 A（-2，4），B（-2，3），C（-1，3），D（-1， 4），将正方形ABCD向下平移7个单位长度，再向右 平移8个单位长度，两次平移后四个顶点相应变为点 E，F，G，H． （1）点E，F，G，H的坐标分别是什么？ 问题5　如图4，正方形ABCD四个顶点的坐标分别是 A（-2，4），B（-2，3），C（-1，3），D（-1， 4），将正方形ABCD向下平移7个单位长度，再向右 平移8个单位长度，两次平移后四个顶点相应变为点 E，F，G，H． （2）如果直接平移正方形ABCD，使点A移到点E， 它和我们前面得到的正方形位置相同吗？ 　　点E，F，G，H的坐标分别是：（6，-3）， （6，-4），（7，-4），（7，-3）．若直接平移 正方形ABCD，使点A移到点E，它就和我们前面 得到的正方形位置相同． 巩固应用 拓展延伸 练习　如图5，将平行四边形ABCD向左平移2 个单位长度，向上平移3个单位长度，可以得到 平行四边形A'B'C'D'，画出平移后的图形，并指 出其各个顶点的坐标. 各个顶点的坐标是 A'（-3，1）； B'（1，1）； C'（2，4）； D'（-2，4）． 回顾本节课所学的主要内容，回答以下问题： （1）点沿坐标轴方向平移后坐标的变化规律是 什么？ （2）将一个图形依次沿两个坐标轴方向平移所 得到的图形，可以通过将原来的图形做一次平移得 到吗？请举例说明． 回顾小结 归纳提升