2016-2017 学年度上学期瓦房店市高级中学高二期中考试 数学试题（文科）

2016-2017 学年度上学期瓦房店市高级中学高二期中考试 数学试题（文科）

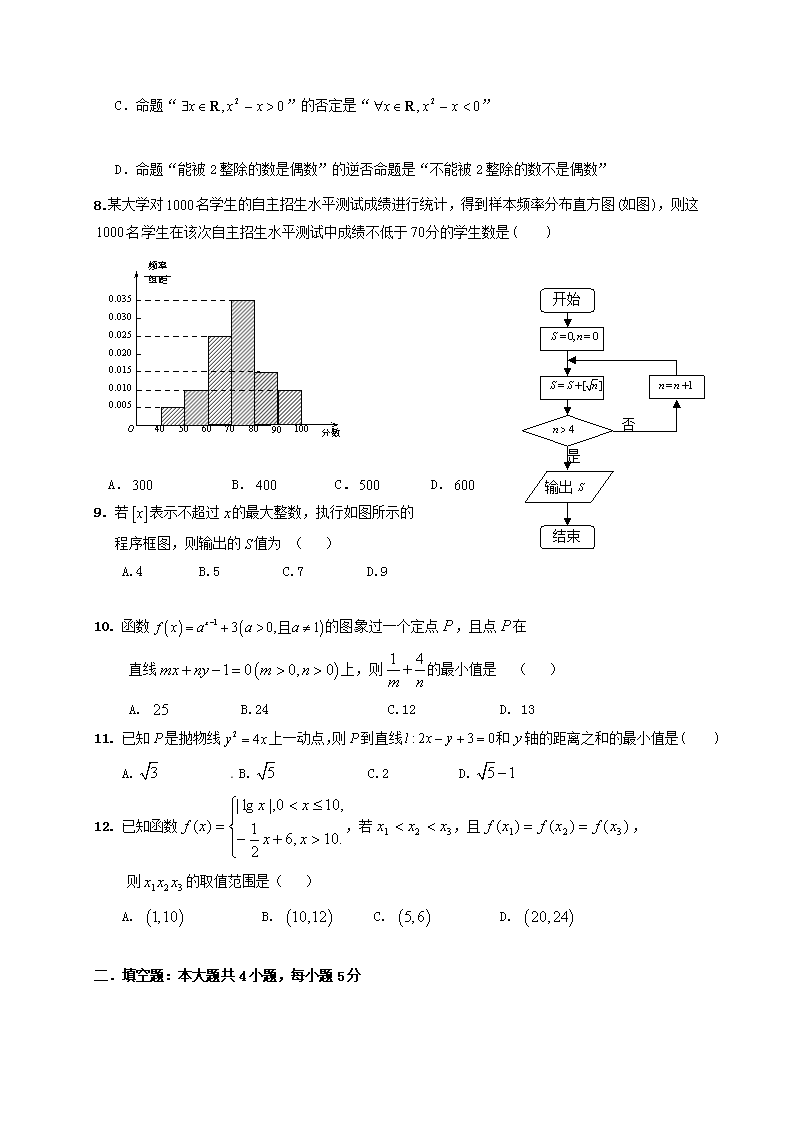
2016-2017 学年度上学期瓦房店市高级中学高二期中考试 数学试题（文科） 时间：120 分钟 满分：150 分 一．选择题：本大题共 12 小题，每小题 5 分，在每小题给出的四个选项中，只有一项是符合题目要 求的. 1. 设全集 }5,4,3,2,1{U ,集合 }2,1{A , }5,3,2{B ,则 BACU )( ( ) A． 3,5 B． 3,4,5 C． 2,3,4,5 D． 1,2,3,4 2. 已知向量  3,4a   ，  1,b m ，若  a a b    ， 则 m  ( ) A．11 2 B．7 C．－7 D． 11 2  3. 某高级中学有高一、二、三三个年级的学生共 1600 名，其中高三学生 400名，如果通过分层抽 样的方法从全体高中学生中抽取一个容量为 80 人的样本，则应从高三年级学生中抽取的人数是 ( ) A．40 B．30 C．20 D．10 4. 北宋欧阳修在《卖油翁》中写道：“（翁）乃取一葫芦置于地，以钱覆其扣，徐以杓酌油沥之，自 钱孔入，而钱不湿．因曰：‘我亦无他，唯手熟尔．’”可见技能都能通过反复苦练而达至熟能生巧 之境的．若铜钱是半径为 1cm 的圆，中间有边长为 0.5cm 的正方形孔，你随机向铜钱上滴一滴油， 则油（油滴的大小忽略不计）正好落入孔中的概率为 （ ） [来源:Z-x-x-k.Com]BB[来源:Z-x-x-k.BB A. 1  B. 1 4 C. 1 2 D. 1 4 5. 直线 03  yx 被圆 2)2()2( 22  yx 截得的弦长等于 ( ) A． 6 B． 3 C． 32 D． 2 6 6. 某公司为确定明年投入某产品的广告支出，对近 5年的广告支出 m 与销售额t （单位：百万元） 进行了初步统计，得到下列表格中的数据： 经测算,年广告支出 m 与年销售额t 满足线性回归方程 6.5 17.5t m  ,则 p 的值为( ) A． 45 B．50 C．55 D． 60 7. 下列结论正确的是( ) A. “ 1x ”是“ 12 x ”的充分不必要条件 t 30 40 p 50 70 m 2 4 5 6 8 B．若“ qp  ”与“ qp  ”都是假命题，则 p 真 q 假 C．命题“ 0, 2  xxx R ”的否定是“ 0, 2  xxx R ” D．命题“能被 2 整除的数是偶数”的逆否命题是“不能被 2 整除的数不是偶数” 8. 某大学对1000 名学生的自主招生水平测试成绩进行统计，得到样本频率分布直方图(如图)，则 这1000 名学生在该次自主招生水平测试中成绩不低于 70 分的学生数是( ) O 40 50 60 70 80 90 100 分数 0.005 0.010 0.015 0.020 0.025 0.030 0.035 频率 组距 A．300 B． 400 C． 500 D． 600 9. 若 x 表示不超过 x 的最大整数，执行如图所示的 程序框图，则输出的 S 值为 （ ） A.4 B.5 C.7 D.9 10. 函数    1 3 0, 1xf x a a a   且 的图象过一个定点 P ，且点 P 在 直线  1 0 0, 0mx ny m n     上，则 1 4 m n  的最小值是 （ ） A. 25 B.24 C.12 D. 13 11. 已知 P 是抛物线 2 4y x 上一动点，则 P 到直线 : 2 3 0  l x y 和 y 轴的距离之和的最小值是 ( ) A. 3 B. 5 C.2 D. 5 1 12. 已知函数       .10,62 1 ,100|,lg| )( xx xx xf ，若 321 xxx  ，且 )()()( 321 xfxfxf  ， 则 321 xxx 的取值范围是（ ） A.  1,10 B.  10,12 C.  5,6 D.  20,24 4n  [ ]S S n  S 否 是 输出 结束 开始 0, 0S n  1n n  二．填空题：本大题共 4 小题，每小题 5 分 13. 若 3 1)6sin(  ，则  )23 2cos(  ________. 14. 已知实数 9,,1 m 成等比数列，则圆锥曲线 12 2  ym x 的离心率为_________. 15. 一个多面体的三视图如图所示，则该多面体的体积是_______. 16. 某高科技企业生产产品 A 和产品 B 需要甲、乙两种新型材料.生产一件 产品 A 需要甲材料 1.5kg，乙材料 1kg，用 5 个工时；生产一件产品 B 需要 甲材料 0.5kg，乙材料 0.3kg，用 3 个工时，生产一件产品 A 的利润为 2100 元，生产一件产品 B 的利润为 900 元.该企业现有甲材料 150kg，乙材料 90kg，则在不超过 600 个工时的条件下，生产产品 A、产品 B 的利润之和 的最大值 为 元. 三．解答题：解答应写出文字说明，证明过程或演算步骤. 17.（本小题满分 10 分） 已知函数 2( ) sin(2 ) 2cos 16f x x x    . （1）求函数 ( )f x 的单调增区间； （2）在 ABC 中， a b c、 、 分别是角 A B C、 、 的对边，且 11, 2, ( ) 2a b c f A    ， 求 ABC 的面积. 18.（本小题满分 12 分） 如 图 ， 在 四 棱 锥 P ABCD 中 ， 侧 面 PAB  底 面 ABCD ， 且 90PAB ABC     ， //AD BC ， 2PA AB BC AD   ， E 是 PC 的中点． （1）求证： //DE 平面 PAB ； （2）求证：平面 PCD  平面 PBC ． 19.（本小题满分 12 分） 某家电专卖店试销 A，B，C 三种新型空调，销售情况记录如下： 第一周 第二周 第三周 第四周 第五周 A 型数量（台） 10 10 15 A4 A5 B 型数量（台） 10 12 13 B4 B5 C 型数量（台） 15 8 12 C4 C5 （1）求 A 型空调前三周的平均周销售量； （2）为跟踪调查空调的使用情况，根据销售记录，从该家电专卖店前三周售出的所有空调中随 机抽取一台，求抽到的空调“是 B 型空调或是第一周售出空调”的概率； （3）根据 C 型空调连续 3 周销售情况，预估 C 型空调连续 5 周的平均周销量为 10 台．当 C 型 空调周销售量的方差最小时，求 C4，C5 的值． 参考公式： 样本数据 nxxx ,,, 21  的方差是： 2 2 2 2 1 2 1 [( ) ( ) ( ) ]ns x x x x x xn       ， 其中 x 为样本平均数． 20.（本小题满分 12 分） 已知数列{ }na 的前 n 项和 nnSn 22  . (1)求数列{ }na 的通项公式 na ； (2)令 3 n n n ab  ，求数列{ }nb 的前 n 项和 nT . 21.（本小题满分 12 分） 垂直于 x 轴的直线l 与椭圆C ： 2 2 14 x y  相交于 M N、 两点， A 是C 的左顶点． （1）求 AM AN  的最小值； （2）设点 P 是C 上异于 M N、 的任意一点，且直线 MP NP、 分别与 x 轴交于 R S、 两点， O 是坐标原点，求 OPR 和 OPS 的面积之积的最大值． 22.（本小题满分 12 分） 已知函数 xxf ln)(  ， baxxg  2 1)( . （1）若 )(xf 与 )(xg 在 1x 处相切，试求 )(xg 的表达式； （2）若 ( 1)( ) ( )1 m xx f xx    在 ),1[  上是减函数，求实数 m 的取值范围； （3）证明不等式： 1 2 n n )1ln( 1 4ln 1 3ln 1 2ln 1  n . 2016-2017 学年度上学期瓦房店市高级中学高二期中考试 数学参考答案（文科） 一、选择题 二、填空题 13、 9 7 14、 3 6 或 2 15、 3 23 16、216000 三、解答题 17、解：（1）∵ ( )f x  2sin(2 ) 2cos 16x x   = 3 1sin2 cos2 cos22 2x x x  = 3 1sin2 cos22 2x x =sin(2 )6x  . ………………(3 分) ∴函数 ( )f x 的单调递增区间是[ , ] ( )3 6k k k Z     .------------(5 分) （2）∵ 2 1)( Af ，∴ 1sin(2 )6 2A   . 又 0 A   ，∴ 1326 6 6A     . ∴ 52 ,6 6 3A A    故 . -----------------(7 分) 在 ABC 中，∵ 1, 2, 3a b c A     ， ∴ 2 21 2 cosb c bc A   ,即1 4 3bc  . ∴ 1bc  . ----------------(9 分) ∴ ABCS 1 3sin .2 4bc A  -----------------(10 分) 18、（1）证明：取 PB 中点 F ，连接 ,EF AF ， 由已知 // //EF BC AD ，且 2 2EF AD BC  ， 所以，四边形 DEFA 是平行四边形， 于是 //DE AF ， AF  平面 PAB ， DE  平面 PAB ， 因此 //DE 平面 PAB ． …………………………………………………(6 分) （2）侧面 PAB  底面 ABCD ， 且 90PAB ABC     所以 BC  平面 PAB ， AF  平面 PAB ，所以 AF BC ， 又因为 PA AB ， F 是 PB 中点，于是 AF PB ， PB BC B ， 所以 AF  平面 PBC ， 由（Ⅰ）知 //DE AF ，故 DE  平面 PBC ， 而 DE  平面 PCD ， 因此平面 PCD  平面 PBC ． ……………………………………(12 分) 19、解：（1） A 型空调前三周的平均销售量 3 35 3 151010 x （台）． 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 A B C B A D B D C A D B …………（2 分） （2）方法 1：从前三周售出的所有空调中随机抽取一台，有 105 种可能，其中“是 B 型或是第 一周售出空调”有35 35 10 60   ． …………（4 分） 因此抽到的空调“是 B 型或是第一周售出空调”的概率是 60 4 105 7P   ． …………（6 分） 方法 2：设抽到的空调“不是 B 型也不是第一周售出空调”的事件是 M ，抽到的空调“是 B 型 或是第一周售出空调”的事件是 N ，则 10 15 8+12 3( ) 35 30 40 7P M     ， 3 4( ) 1 7 7P N    ． …………（4 分） 故抽到的空调“是 B 型或是第一周售出空调”的概率是 4 7 ． …………（6 分） （3）因为 C 型空调平均周销售量为10 台，所以 4 5 10 5 15 8 12 15c c       ． …………（8 分） 又 2 2 2 2 2 2 4 5 1[(15 10) (8 10) (12 10) ( 10) ( 10) ]5s c c          ， 化 简 得 到 2 2 4 1 15 91[2( ) ]5 2 2s c   ． …………（10 分） 注意到 4c  N ，所以当 4 7c  或 4 8c  时， 2s 取得最小值． …………（11 分） 所以当 4 5 7 8 c c    或 4 5 8 7 c c    时， 2s 取得最小值． …………（12 分） 20、解：（1）当 1n 时， 12111  Sa ………… 2 分 当 2n 时， 32)]1(2)1[(2 22 1   nnnnnSSa nnn …… 4 分 又 31211 a 也符合上式，………… 5 分 因此， 32  nan ………… 6 分 （2） nn nb 3 32  nnn nnT 3 1)32( 3 1)52( 3 13 3 113 11 132   ……………. ③ 1432 3 1)32( 3 1)52( 3 13 3 11 3 113 1  nnn nnT  ……… ④ ③-④得 132 3 1)32() 3 1 3 1 3 1(23 1 3 2  nnn nT  …………………… 9 分 整理得 nn nT 3  …………………… 12 分 21、解：（1）点 M N、 关于 x 轴对称，设 1 1 1( )( 0)M x y y , ，则 1 1( )N x y, ， ∵ ( 2,0)A  ，∴ 1 1( 2, )AM x y  ， 1 1( 2, )AN x y   ， ∵点 M 在C 上，∴ 2 2 1 1 1 4 xy   ， …………（4 分） ∴ ,5 1)5 8 4 5344 5)2( 2 11 2 12 1 2 1  xxxyxANAM （ ∵ 1 ( 2,2)x   ，∴ 1 8 5x   时， AM AN  取最小值 1 5  ， …………（6 分） （2）设 0 0( )P x y, ，则直线 MP 的方程为： 0 1 0 0 0 1 ( )y yy y x xx x    ， 令 0y  ，得 1 0 0 1 0 1 R x y x yx y y   ，同理 10 1001 yy yxyxxS   ， …………（8 分） ∵点 M 、 P 在C 上，∴ 2 2 1 14(1 )x y  ， 2 2 0 04(1 )x y  ， ∴ 2 2 2 2 2 2 1 0 0 1 0 1 2 2 2 2 0 1 0 1 4(1 ) (1 ) 4( ) 4R S y y y y y yx x y y y y         ， …………（10 分） 2 2 0 0 0 0 1 1 1| || | | || | | |2 2 4OPS OPR S RS S OS y OR y x x y y      ， ∵ 0 [ 1,1]y   ，∴ 0 1y   时， OPS OPRS S  取最大值 1． …………（12 分） 22、解：（1）由已知 且 xxf 1)(  af 2 11)1(  得： 2a ------------------(2 分) 又 bag  2 10)1(  1b  1)(  xxg -------------(3 分) （2） ( 1)( ) ( )1 m xx f xx     ( 1) ln1 m x xx   在 ),1[  上是减函数， 0 )1( 1)22()( 2 2    xx xmxx 在 ),1[  上恒成立. ------------- (5 分) 即 01)22(2  xmx 在 ),1[  上恒成立，由 xxm 122  ， ),1[ x ),2[1  xx 222  m 得 2m --------------(7 分) （3)由（1）可得：当 2x 时： )1(21ln  xxxx )1(2 1ln  xxx 得： xxx ln 1 )1( 2  xxx ln 1)1 1 1(2  -----------------(9 分) 当 2x 时： 2ln 1)2 1 1 1(2  当 3x 时： 3ln 1)3 1 2 1(2  当 4x 时： 4ln 1)4 1 3 1(2  …… 当 1 nx 时： )1ln( 1)1 11(2  nnn ， 2,   nNn 上述不等式相加得：  )1 11(2 n )1ln( 1 4ln 1 3ln 1 2ln 1  n 即： 1 2 n n )1ln( 1 4ln 1 3ln 1 2ln 1  n -----------------(12 分)