- 2021-04-26 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2021版高考数学一轮复习高考命题新思维之四课件文北师大版
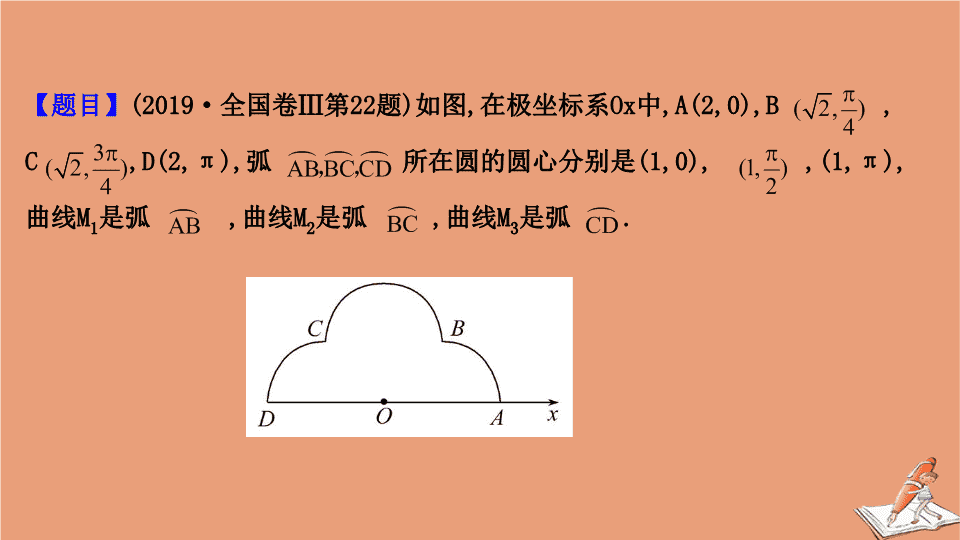
高考命题新思维之四 “ 云朵 ” 考题别有创意 基础稳固轻松求解 【 题目 】 (2019· 全国卷 Ⅲ 第 22 题 ) 如图 , 在极坐标系 Ox 中 ,A(2,0),B , C ,D(2,π), 弧 所在圆的圆心分别是 (1,0), ,(1,π), 曲线 M 1 是弧 , 曲线 M 2 是弧 , 曲线 M 3 是弧 . (1) 分别写出 M 1 ,M 2 ,M 3 的极坐标方程 . (2) 曲线 M 由 M 1 ,M 2 ,M 3 构成 , 若点 P 在 M 上 , 且 |OP|= , 求点 P 的极坐标 . 【 试题点评 】 本题命制新颖 , 别出心裁 , 以一个“云”形状的图形 , 要求考生求极坐标方程 . 这种极坐标形式的问题在高考中不多见 . 命题人的“煞费苦心”让考生感觉这朵云“好凄美” . 这些题目看似变难了 , 其实是出题方式变得灵活了 , 更加符合新高考的要求 , 突出考查数学建模、直观想象、数学运算的核心素养 . 【 命题探源 】 在 2016 年上海高考数学试卷中 , 也出现过类似给出图形求曲线的极坐标方程的题目 , 其来源为数学家笛卡尔的心形线 . 人教版教材中 , 也出现过自己选择适当的极坐标系求圆的极坐标方程、直线的极坐标方程等 . 【 高考声音 】 这道题传递了一个高考信息 , 回归课本 , 基础要绝对扎实 . 虽然题目比较新颖 , 但是只要紧扣教材 , 就能很好地解答 . 这些试题不仅对所学的知识进行考查 , 而且还与实际生活联系得更加紧密了 . 高考试题不但考查考生的做题的速度和准确度 , 还拓宽了知识的广度和宽度 , 更加考验学生对知识灵活运用的能力 . 【 解法探究 】 (1) 将三个过原点的圆方程列出 , 注意题中要求的是弧 , 所以要注意方程中 θ 的取值范围 . (2) 根据条件 ρ= 逐个方程代入求解 , 最后解出 P 点的极坐标 . 【 解析 】 (1) 如图所示 , 极坐标 A(2,0),B ,C ,D(2,π) 转化为直角坐标为 A(2,0),B(1,1),C(-1,1),D(-2,0). 则 M 1 ,M 2 ,M 3 的圆心坐标分别为 (1,0),(0,1),(-1,0). M 1 ,M 2 ,M 3 所在圆的方程为 (x-1) 2 +y 2 =1,x 2 +(y-1) 2 =1,(x+1) 2 +y 2 =1, 设 x=ρ cos θ,y=ρ sin θ, 则 M 1 ,M 2 ,M 3 所在圆的极坐标方程分别为 M 1 : ρ =2cos θ , M 2 : ρ =2cos =2sin θ , M 3 : ρ =2cos( θ - π )=-2cos θ . (2) 设 P(ρ,θ), 由题设及 (1) 知若 2cos θ= , 解得 θ= , 若 2sin θ= , 解得 θ= 或 θ= . 若 -2cos θ= , 解得 θ= . 故 P 的极坐标为 【 拓展赏析 】 1. 其实这道题并不难 : 考生之所以认为这道题难 , 其主要原因是长期的应试训练 , 造成了学生思维的僵化的结果 . 由于没有心理准备 , 当面对新的变化时容易引起情绪上的波动 , 从而觉得试题变难了 . 其实只要静下心来好好读读题目 , 也不难发现那是几个曲线的组合 . 教材上的标准模型不见了 , 取而代之的是几个标准模型的组合 . 2. 把高考拉进了现实 : 现实社会中哪有标准的模型 , 几乎每件事都是复杂的不能再复杂的事情的组合 . 要想解决现实的问题 , 只有努力地透过现象看本质 , 找出其中所包含的模型 , 才有可能解决现实中的问题 .“ 死记硬背”“机械刷题”“题海战术” , 已不适合新高考 . 高考试卷中出现了一朵云 , 这朵云把高考拉进了现实 . 值得师生在备考中细加品味 . 【 新题试做 】 (2019· 北京高考 ) 数学中有许多形状优美、寓意美好的曲线 , 曲线 C:x 2 +y 2 =1+|x|y 就是其中之一 ( 如图 ). 给出下列三个结论 : ① 曲线 C 恰好经过 6 个整点 ( 即横、纵坐标均为整数的点 ); ② 曲线 C 上任意一点到原点的距离都不超过 ; ③ 曲线 C 所围成的“心形”区域的面积小于 3. 其中 , 所有正确结论的序号是 ( ) A.① B.② C.①② D.①②③ 【 解析 】 选 C. 对① , 令 x=0 得 y=±1, 即曲线 C 过整点 (0,±1); 令 x=1 得 1+y 2 =1+y,y=0,1, 即曲线 C 过整点 (1,0),(1,1), 又由曲线关于 y 轴对称知 , 曲线 C 过整点 (-1,0),(-1,1), 结合图形知 , 曲线 C 不过其他整点 , 所以①正确 ; 对② , 只需考虑第一象限内的点 , 即 x>0,y>0, 设 C 上的点 (x,y) 到原点的距离为 d, 则 x 2 +y 2 =1+|x|y=1+xy≤1+ ,x 2 +y 2 ≤2,d≤ , 所以②正确 ; 对③ , 由①知 ,S △OAB = ×1×1= ,S 正方形 OBCD =1×1=1, 所以 S 阴影 =2× =3, 所以心形区域面积大于 3,③ 错误 .查看更多