数学高考试题分析 专题六 导数及其应用

数学高考试题分析 专题六 导数及其应用

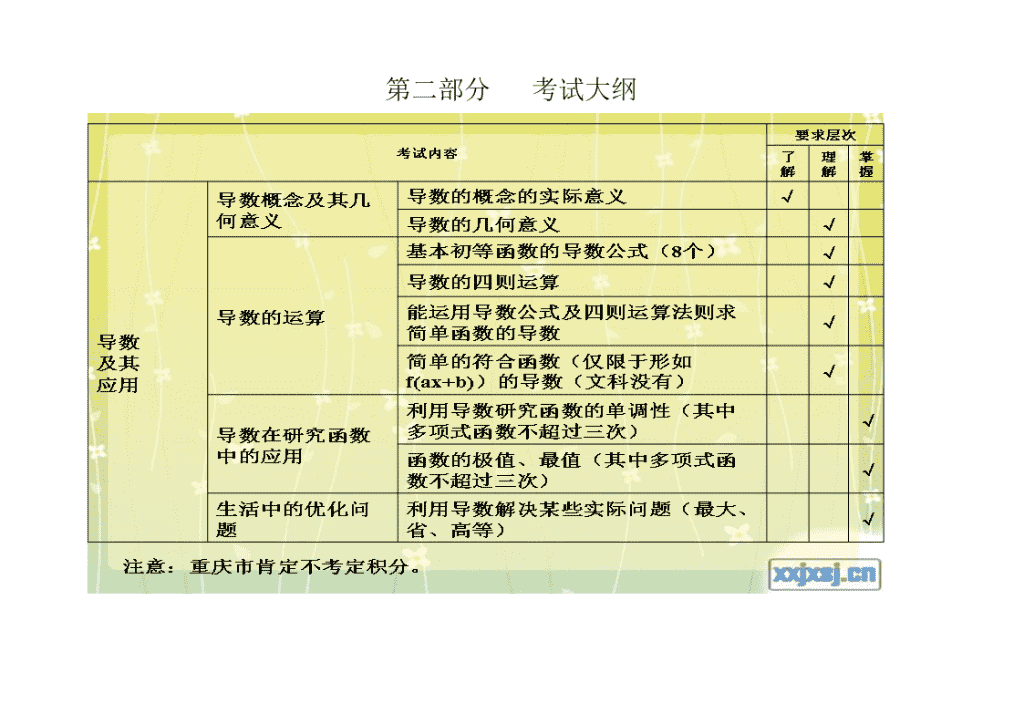
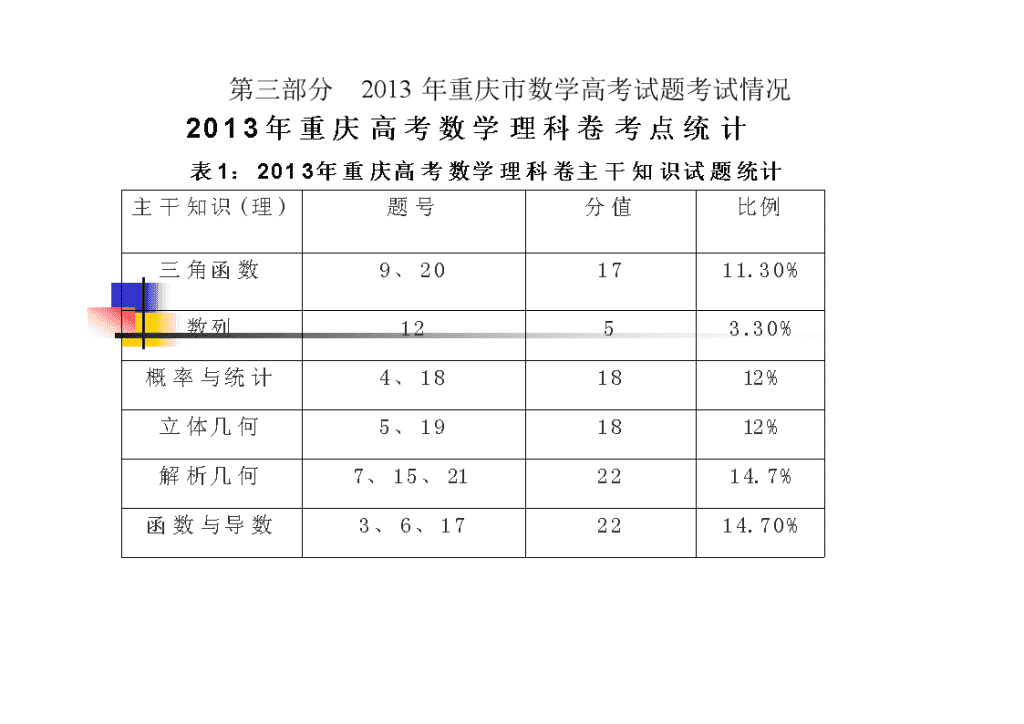
数学高考试题分析 专题六 导数及其应用 第一部分 高中数学新课程标准 ‎1．导数及其应用（约24课时）‎ ‎（1）导数概念及其几何意义 ‎①通过对大量实例的分析，经历由平均变化率过渡到瞬时变化率的过程，了解导数概念的实际背景，知道瞬时变化率就是导数，体会导数的思想及其内涵。‎ ‎②通过函数图象直观地理解导数的几何意义。‎ ‎（2）导数的运算 ‎① 能根据导数定义求函数y=c，y=x，y=x2，y=x3,y=1/x的导数。‎ ‎②能利用给出的基本初等函数的导数公式和导数的四则运算法则求简单函数的导数，能求简单的复合函数（仅限于形如f（ax+b））的导数。‎ ‎③ 会使用导数公式表。‎ ‎（3）导数在研究函数中的应用 ‎①结合实例，借助几何直观探索并了解函数的单调性与导数的关系（参见选修1-1案例中的例4）；能利用导数研究函数的单调性，会求不超过三次的多项式函数的单调区间。‎ ‎②结合函数的图象，了解函数在某点取得极值的必要条件和充分条件；会用导数求不超过三次的多项式函数的极大值、极小值，以及闭区间上不超过三次的多项式函数最大值、最小值；体会导数方法在研究函数性质中的一般性和有效性。‎ ‎（4）生活中的优化问题举例。‎ 例如，通过使利润最大、用料最省、效率最高等优化问题，体会导数在解决实际问题中的作用。‎ 第二部分 考试大纲 第三部分 2013年重庆市数学高考试题考试情况 知识版块 题号 分值 考查内容 集合 ‎ ‎1‎ ‎5‎ 集合的交、并、补 函数与导数 ‎ ‎3、6、17‎ ‎22‎ 函数单调性，求切点，导数及其应用 ‎ 三角函数 ‎ ‎9、20‎ ‎17‎ 三角公式、求值、余弦定理、弦切互化 平面向量 ‎ ‎10‎ ‎5‎ 向量和圆的最值问题，转化 数列 ‎ ‎12‎ ‎5‎ 等比数列的基本运算 不等式 ‎3、16、‎ ‎10‎ 基本不等式、恒成立问题 复数 ‎11‎ ‎5‎ 复数的有关概念, 复数的四则运算 推理与证明 ‎2、22‎ ‎17‎ 全称、特称命题，新概念及集合的划分 算法初步 ‎8‎ ‎5‎ 流程图、对数换底公式（该题非常巧妙）‎ 概率统计（计数）‎ ‎4、13、18‎ ‎23‎ 茎叶图、中位数、平均数、古典概型， 分布列期望 立体几何 ‎5、19‎ ‎18‎ 三视图、直棱柱性质、线线、线面平行与垂直、空间坐标 直线与圆 ‎7、15、‎ ‎10‎ 直线与圆，极坐标与参数方程 圆锥曲线 ‎21‎ ‎12‎ 求椭圆的离心率 第四部分 考试细目表分析