2020届高三数学上学期第二次月考试题 文（含解析）(新版)新人教版

2020届高三数学上学期第二次月考试题 文（含解析）(新版)新人教版

- 1 - 2019 高三上学期第二次月考数学 (文科) 一、选择题：共 12 题 1. 集合 ,集合 ,则 A. B. C. D. 【答案】D 【解析】因为集合 ,集合 , 所以 . 故选 D. 2. 复数 的共轭复数是 A. B. C. D. 【答案】B 【解析】复数 = 的共轭复数是 . 故选 B. 3. 已知命题 对于 恒有 成立;命题 奇函数 的图象必过原点,则下列结论正 确的是 A. 为真 B. 为假 C. 为真 D. 为真 【答案】D 【解析】因为 等价于 ,故命题 p 是真命题; 函数 为奇函数,但函数 的图象不过原点,故命题 q 是假命题, 则命题 是真命题,故 是真命题. 故选 D. 4. 已知 则 的值是 A. B. C. D. 【答案】B 【解析】试题分析：由于 ， ， - 2 - ， ，故答案为 B． 考点：同角三角函数的基本关系． 5. 在等差数列 中,若 ,那么 等于 A. 4 B. 5 C. 9 D. 18 【答案】B 【解析】设等差数列的公差为 d,则 = , = ,所以 d=2,a1= ,则 故选 B. 6. 设 为实数,函数 的导函数为 ,且 是 偶函数,则曲线: 在点 处的切线方程为 A. B. C. D. 【答案】A 【解析】 是偶函数,所以 a=0, ， . 则 ,所以切线方程为 9x-y-16=0. 故选 A. 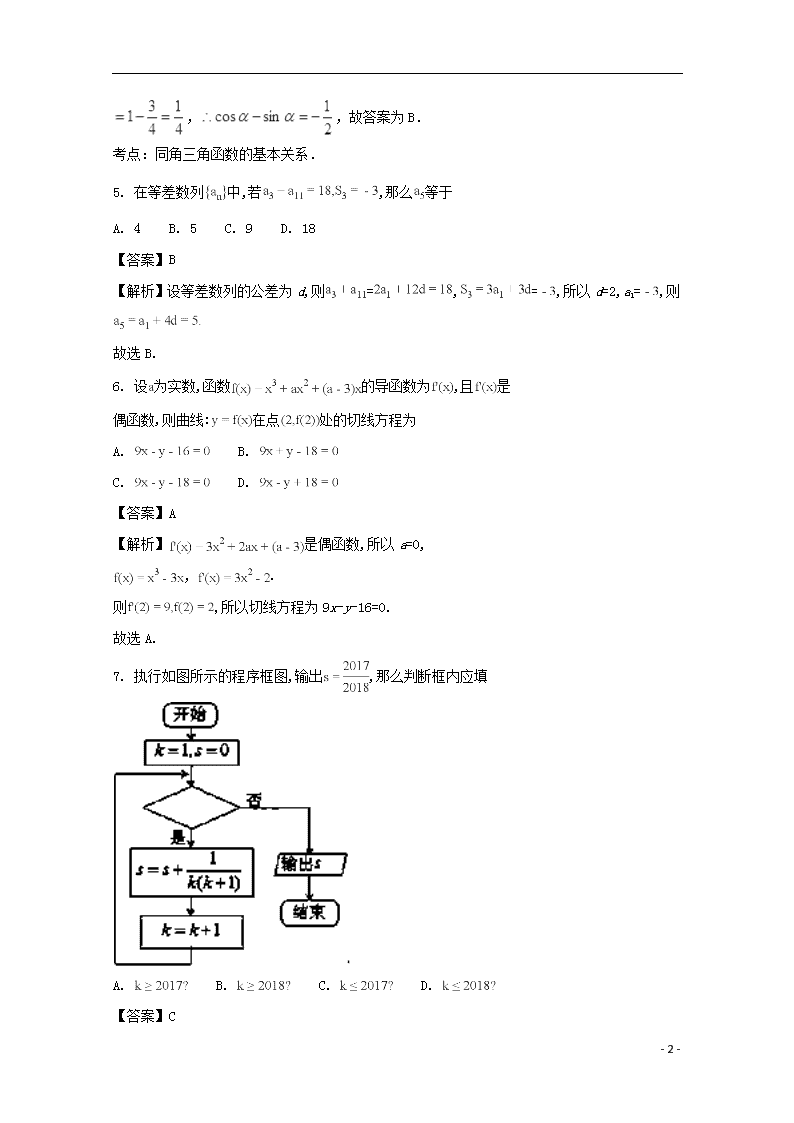7. 执行如图所示的程序框图,输出 ,那么判断框内应填 A. B. C. D. 【答案】C - 3 - 【解析】因为 ,所以 ,因为输出 ,所以此时 k=2018, 故选 C. 点睛:本题考查的是算法与流程图,对算法与流程图的考查，侧重于对流程图循环结构的考查. 要先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起 点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求 和还是求项. 8. 若 a>b>0,cb>0,所以 . 所以 . 故选 C. 9. 已知△ABC 的一个内角为 120°,且三边长构成公差为 2 的等差数列,则 △ABC 的面积为 A. B. C. 30 D. 15 【答案】A 【解析】由题意,设这三边长分别为 a,a+2,a+4,由余弦定理可得 (a+4)2=a2+(a+2)2-2a(a+2)cos120°,所以 a=3,则这三条边长分别为 3,5,7,则△ABC 的面积 S= . 故选 A. 10. 在 中, ,且 ,点 满足 ,则 等于 A. 3 B. 2 C. 4 D. 6 【答案】D 【解析】以点 C 为原点,建立平面直角坐标系,A(3,0),B(0,3),因为 ,所以 M(2,1),则 - 4 - ,所以 故选 D. 11. 已知关于 x 的不等式 x2-4ax＋6a2<0(a>0)的解集为(x1,x2),则 x1＋x2＋ 的最小值是 A. B. C. D. 【答案】C 【解析】由题意可知,x1,x2 是方程 x2-4ax＋6a2=0 两个根,则 , 所以 x1＋x2＋ ,当且仅当 时,等号成立. 故选 C. 点睛：在用基本不等式求最值时，应具备三个条件：一正二定三相等.①一正：关系式中，各 项均为正数；②二定：关系式中，含变量的各项的和或积必须有一个为定值；③三相等：含 变量的各项均相等，取得最值. 12. 已知向量 是两个互相垂直的单位向量,且 ,则对任意的正实数 的最小值是 A. 2 B. C. 4 D. 【答案】D 【解析】因为向量 是两个互相垂直的单位向量,所以 ,又因为 ,所以 = = ,当且仅当 ,即 t=1 时,等号成立,故 的最小值为 . 故选 D. 点睛：（1）平面向量中涉及有关模长的问题时，常用到的通法是将模长进行平方，利用向量 数量积的知识进行解答，很快就能得出答案； （2）在用基本不等式求最值时，应具备三个条件：一正二定三相等.①一正：关系式中，各 项均为正数；②二定：关系式中，含变量的各项的和或积必须有一个为定值；③三相等：含 变量的各项均相等，取得最值. 二、填空题：共 4 题 13. 已知向量 ,若 ,则实数 的值为___________. 【答案】-1 - 5 - 【解析】因为 ,所以 , ,因为 ,所以 ,所以 答案为：-1. 14. 设 x,y 满足约束条件 则 z＝2x-y 的最大值为____________. 【答案】8 【解析】试题分析：线性约束条件对应的可行域为直线 围成 的三角形及内部，顶点为 ，当 z＝2x－y 过点 时取得最大值 8 考点：线性规划问题 15. 已知 是等差数列 的前 项和,且 ,给出下列五个命题: ① ;② ;③ ;④数列 中的最大项为 ;⑤ . 其中正确命题的是___________. 【答案】①② 16. 已知 ,当 取最小值时,则 ___________. 【答案】 【解析】由 ，知 . 以点 O 为原点建立平面直角坐标系,A(4,0),B(0,3),则 = = ,所以 = = , 当 时, 取得最小值,则 = . - 6 - 答案为： . 点睛：平面向量中涉及有关模长的问题时，常用到的通法是将模长进行平方，利用向量数量 积的知识进行解答，很快就能得出答案；另外，向量是一个工具型的知识，具备代数和几何 特征，在做这类问题时可以使用数形结合的思想，会加快解题速度. 三、解答题：共 7 题 17. 已知函数 的最大值为 . (1)求常数 的值及函数 的单调递增区间; (2)若将 的图象向左平移 个单位,得到函数 的图象,求函数 在区间 上的值域. 【答案】（1） 单调递增区间为 ；（2） . 【解析】试题分析：(1)化简 ,由函数的最大值求出 a,再利用正弦函数的性 质求单调区间; (2)由图象变换可得 ,结合正弦函数的性质即可求出值域. 试题解析： (1) = = = , . 由 , 解得 , . 所以函数 的单调递增区间为 . (2) 将 的图象向左平移 个单位,得到函数 的图象, , , , 所以 值域为 18. 已知{an}是等差数列,{bn}是等比数列,且 b2=3,b3=9,a1=b1,a14=b4. (1)求{an} , {bn}的通项公式; - 7 - (2)设 cn=an+bn,求数列{cn}的前 n 项和. 【答案】（1） ；（2） . 【解析】试题分析：(1)已知可得等比数列的首项与公比,进而可得等差数列的首项与公差,则 易得两个数列的通项公式; (2)利用等差数列与等比数列的前 n 项和公式求和即可. 试题解析： (1)等比数列 的公比 , 所以 . . . 设等差数列 的公差为 . 因为 , 所以 ,即 . 所以 . (2)由(1)知, . 因此 . 从而数列 的前 项和 = = = . 19. 在 中,内角 A,B,所对的边分别为 .已知 的面积为 . (1)求 和 的值; (2)求 cos(2A+ )的值. 【答案】（1） ；（2） . 【解析】试题分析：(1)由角 A 的余弦值求出其正弦值,结合三角形的面积公式可求得 ,结合 余弦定理与 可得 a 的值,再利用正弦定理求解可得 的值; - 8 - (2)由(1),利用二倍角公式求出 的值,再利用两角和与差公式求解. 试题解析： (1)在 中,由 ,所以 由 又 可得 , 由余弦定理 , 得 , 由正弦定理 , (2)由(1)得 , , . 20. 已知 是数列 的前 项和,点 满足 ,且 . (1)求数列 的通项公式; (2)令 ,求数列 的前 项和 . 【答案】（1） ；（2） . 【解析】试题分析：(1) ,由 求出 q 的值,再利用 可得数列 的通项公式; (2) ,利用错位相减法与等比数列的前 项和公式求和即可. 试题解析： (1)由题意知: , 时, ; 时, . 由 得, , , . - 9 - 是以 2 为首项,2 为公比的等比数列, . (2)由(1)知: , , ,① ,② ①-②得: = = = , . 点睛：用错位相减法求和应注意的问题(1)要善于识别题目类型，特别是等比数列公比为负数 的情形；(2)在写出“Sn”与“qSn”的表达式时应特别注意将两式“错项对齐”以便下一步 准确写出“Sn－qSn”的表达式；(3)在应用错位相减法求和时，若等比数列的公比为参数， 应分公比等于 1 和不等于 1 两种情况求解. 21. 已知函数 . (1)求 的单调区间; (2)若 ,都有 ,求实数 的取值范围; (3)证明: 且 ). 【答案】（1）见解析；（2） ；（3）见解析. 【解析】试题分析：(1) ,分 两种情况讨论 的符号,即可判断函数的单调 性; (2)结合(1)的结论,求出函数 的最大值,即可得出结论; (3)由(2)知: 时, 在 上恒成立,且 在 上单调递减, ,所以 在 上恒成立,令 ,则 ,再利用放缩法即可证明结论. 试题解析： (1)函数 的定义域为 , ①若 时, 时, , - 10 - 的单调递增区间是 ,单调递减区间是 ; ② 时, 恒成立, 的单调递增区间是 , 综上①②知: 时, 的单调递增区间是 ,无单调递减区间; 时, 的单调递增区间是 ,单调递减区间是 . (2)由(1)知:当 时, 在 上单调递增,且 , 恒成立是假命题; 当 时,由(Ⅰ)知: 是函数的最大值点, , , 故 的取值范围是 . (3)证明:由(2)知: 时, 在 上恒成立, 且 在 上单调递减, , ,即 在 上恒成立. 令 ,则 ,即 , , = , 故 且 ). 点睛：导数问题经常会遇见恒成立的问题： （1）根据参变分离，转化为不含参数的函数的最值问题； （2）若 就可讨论参数不同取值下的函数的单调性和极值以及最值，最终转化 为 ，若 恒成立 ； （3）若 恒成立，可转化为 （需在同一处取得最值） . 22. 在直角坐标系 中,曲线 C1 的参数方程为 (α为参数),以原点 O 为极点,x 轴 - 11 - 的正半轴为级轴,建立极坐标系,曲线 C2 的极坐标方程 ; (1)求曲线 C1 的普通方程和曲线 C2 的直角坐标方程; (2)设 P 为曲线 C1 上的动点,求点 P 到曲线 C2 上的距离的最小值. 【答案】（1）C1 的普通方程为: 曲线 C2：x+y=6；（2） . 【解析】试题分析：(1)消去参数α可得曲线 C1 的普通方程;利用 化简可得曲 线 C2 的直角坐标方程; (2)设椭圆上的点 ,利用点到直线的距离公式,结合三角函数的知识求解即可. 试题解析： (1)由曲线 C1: 为参数), 曲线 C1 的普通方程为: 由曲线 C2:ρsin(π+ )=3 ,展开可得: (sinθ+cosθ)=3 , 化为:x+y=6. (2)椭圆上的点 到直线 O 的距离为 其中 , 所以当 sin(α+φ)=1 时,P 的最小值为 . 23. 已知函数 , (1)解不等式 (2)若对于 ,有 ,求证: . 【答案】（1）(0,2)；（2）见解析. 【解析】试题分析：(1)原不等式等价于﹣x﹣1＜2x﹣1＜x+1,求解可得结论; (2)f(x)=|2(x﹣y﹣1)+(2y+1)|,结合条件,利用绝对值三角不等式证明可得结论. 试题解析： (1)不等式 f(x)＜x+1,等价于|2x﹣1|＜x+1,即﹣x﹣1＜2x﹣1＜x+1, 求得 0＜x＜2,故不等式 f(x)＜x+1 的解集为(0,2). - 12 - (2) , 所以 f(x)=|2x﹣1|=|2(x﹣y﹣1)+(2y+1)|≤|2(x﹣y﹣1)|+|(2y+1)|≤2 + ＜1.