高考理科数学模拟试题
2018届高三复习卷一
数学(理科)
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,
只有一项是符合题目要求的.
1.设集合, ,则
A. B. C. D.
2.已知是虚数单位,复数满足,则的虚部是( )
A. B. C. D. 1
3.在等比数列中, , ,
则数列的前9项的和( )
A. 255 B. 256 C. 511 D. 512
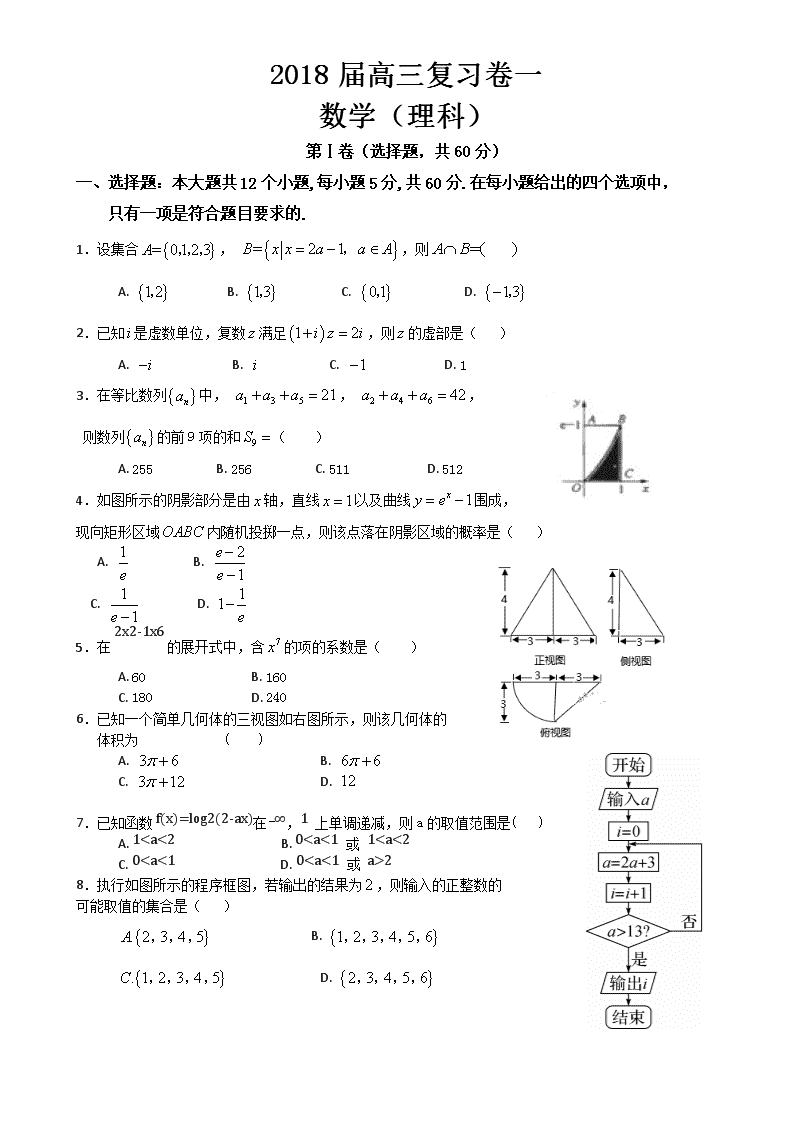
4.如图所示的阴影部分是由轴,直线以及曲线围成,
现向矩形区域内随机投掷一点,则该点落在阴影区域的概率是( )
A. B.
C. D.
5.在2x2-1x6的展开式中,含的项的系数是( )
A. 60 B. 160
C. 180 D. 240
6.已知一个简单几何体的三视图如右图所示,则该几何体的
体积为 ( )
A. B.
C. D.
7.已知函数f(x)=log2(2-ax)在-∞,1 上单调递减,则a的取值范围是( )
A. 1
2
8.执行如图所示的程序框图,若输出的结果为,则输入的正整数的
可能取值的集合是( )
B.
D.
9.上的偶函数满足,当时, ,则
的零点个数为( )
A. 4 B. 8 C. 5 D. 10
10.如图,已知抛物线的焦点为,直线过且依次交
抛物线及圆于点四点,则
的最小值为( )
A. B. C. D.
11.已知函数在区间上是增函数,
且在区间上恰好取得一次最大值,则的取值范围是( )
A. B. C. D.
12.如图,点列{An},{Bn}分别在某锐角的两边上,且,
.()
若 ( )
A.是等差数列 B.是等差数列
C.是等差数列 D.是等差数列
第II卷(非选择题)
二、填空题:本大题共4小题,每小题5分,满分20分.
13.已知平面向量,且,则__________.
14.若变量满足,且恒成立,则的最大值为______________.
15.若双曲线上存在一点满足以为边长的正方形的面积等于
(其中为坐标原点),则双曲线的离心率的取值范围是__________.
16.若曲线与曲线存在公共切线,则的取值范围为__________.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知向量.
(1)求的最大值及取最大值时的取值集合;
(2)在△中, 是角的对边,若且,求△的周长的取值范围.
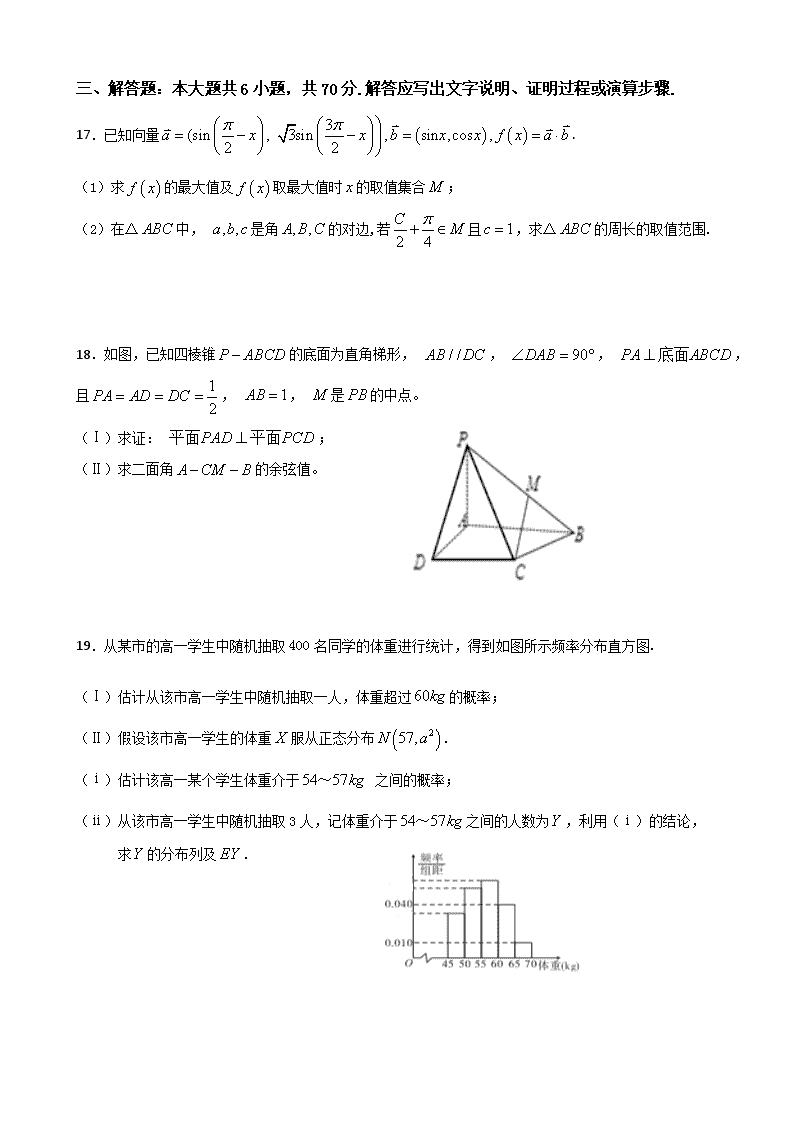
18.如图,已知四棱锥的底面为直角梯形, , , ,且, , 是的中点。
(Ⅰ)求证: ;
(Ⅱ)求二面角的余弦值。
19.从某市的高一学生中随机抽取400名同学的体重进行统计,得到如图所示频率分布直方图.
(Ⅰ)估计从该市高一学生中随机抽取一人,体重超过的概率;
(Ⅱ)假设该市高一学生的体重服从正态分布.
(ⅰ)估计该高一某个学生体重介于 之间的概率;
(ⅱ)从该市高一学生中随机抽取3人,记体重介于之间的人数为,利用(ⅰ)的结论,
求的分布列及.
20.已知右焦点为的椭圆与直线相交于、两点,
且. (1)求椭圆的方程;
(2)为坐标原点,,,是椭圆上不同的三点,并且为的重心,
试探究的面积是否为定值,若是,求出这个定值;若不是,说明理由.
21. 已知函数.
(1)当时,试求函数图像过点的切线方程;
(2)当时,若关于的方程有唯一实数解,试求实数的取值范围;
(3)若函数有两个极值点,且不等式恒成立,
试求实数的取值范围.
请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.
22.【选修4-4:坐标系与参数方程】在直角坐标系中,曲线的参数方程为(为参数),直线的方程为,以为极点,以轴正半轴为极轴,建立极坐标系,
(1)求曲线和直线的极坐标方程;
(2)若直线与曲线交于两点,求.
23.【不等式选讲】已知, .
(1)解不等式;
(2)若不等式恒成立,求实数的取值范围.
参考答案
1.B
【解析】则
2.D【解析】 ,所以的虚部是1,选D.
3.C【解析】由等比数列的通项公式可得,
求解方程组可得: ,则数列的前9项的和.
4.【答案】B
【解析】解答:由题意,阴影部分的面积为dx==e−2,
∵矩形区域OABC的面积为e−1,∴该点落在阴影部分的概率是.
故选B.
5.D【解析】二项式的通项公式为Tk+1=C6k(2x2)6-k(-1x)k=C6k26-k(-1)kx12-52k
,令12-52k=7⇒k=2,所以含x7的项的系数是C6224=240 ,故选D
6.A【解析】由三视图知,该几何体有四分之一圆锥与三棱锥构成,故体积为
,故选A.
7.A【解析】令t=2﹣ax,则原函数化为g(t)=log2t,外层函数g(t)=log2t为增函数,
要使复合函数f(x)=log2(2﹣ax)(﹣∞,1]上单调递减,则内层函数t=2﹣ax在(﹣∞,1)上单调递减,且t=2
﹣ax在(﹣∞,1)上大于0恒成立.∴a>12-a>0,解得:1<a<2.
8.A【解析】循环依次为 ,所以可能取值的集合是,
9.C【解析】∵,∴,故函数的周期T=2。
∵0≤x≤1时,且是R上的偶函数,∴﹣1≤x≤1时, ,
令,画出函数的图象,
如下图所示:由图象得函数和的交点有5个,
10.【答案】C
【解析】由题意得,即为圆的圆心,准线方程
为。
由抛物线的定义得,又,所以。同理。
①当直线与x轴垂直时,则有,∴。
②当直线与x轴不垂直时,设直线方程为,
由消去y整理得,∴,
∴,当且仅当时等号成立。
综上可得。选C。
11、 是函数含原点的递增区间.
又∵函数在上递增,
∴得不等式组 ,得 又∵ 又函数在区间上恰好取得一次最大值,根据正弦函数的性质可知 ,即函数在 处取得最大值,
可得 综上,可得 故选D
12.【答案】A试题分析:表示点到对面直线的距离(设为)乘以长度的一半,即,由题目中条件可知的长度为定值,那么我们需要知道的关系式,由于和两个垂足构成了直角梯形,那么,其中为两条线的夹角,即为定值,那么,,
作差后:,都为定值,所以为定值.故选A.
13.或
【解析】∵,∴, ,又∵,∴,解得或,故答案为或.
14.
【解析】
所以过时, 的最小值为-4,所以的最大值为-4.
15.【解析】由题意, ,又,
则,即,得, ,所以,
所以,即的取值范围是。
16. 【解析】解:由y=ax2(a>0),得y′=2ax,
由y=ex,得y′=ex, 曲线C1:y=ax2(a>0)与曲线C2:y=ex存在公共切线,
设公切线与曲线C1切于点(x1,ax12),与曲线C2切于点,
则, 可得2x2=x1+2,∴ ,
记,则 ,
当x∈(0,2)时,f′(x)<0,f(x)递减;当x∈(2,+∞)时,f′(x)>0,f(x)递增。
∴当x=2时, . ∴a的范围是 .
17.(1),;(2).试题解析:(1),
,
的最大值为,此时
即
(2) , ,
由得
又, 故,即周长的范围为.
18.(Ⅰ)证明见解析;(Ⅱ)
证明:(Ⅰ)以为坐标原点长为单位长度,如图,建立空间直角坐标系,则各点为, , , , , ,则, ,故,所以,由题设知,且与是平面内的两条相交直线,由此得,又在平面内,故平面。
(Ⅱ)在上取一点,则存在,使,连接, , ,所以, , 。要使,只要,即,解得。可知当时, 点坐标为,能使,此时, , ,所以。由, , ,所以,故所求二面角的余弦值为。
19.(1)(2)(ⅰ)(ⅱ)见解析
(Ⅰ)这400名学生中,体重超过的频率为,
由此估计从该市高一学生中随机抽取一人,体重超过的概率为.
(Ⅱ)(ⅰ)∵, ,∴,
∴,∴.
(ⅱ)因为该市高一学生总体很大,所以从该市高一学生中随机抽取3人,可以视为独立重复实验,
其中体重介于之间的人数, , .
所以的分布列为
.
20.【答案】(1);(2).
【解析】(1)设,,则,
∴,即①,∵,∴,即②,
∴由①②得,又,, ∴椭圆的方程为.
(2)设直线方程为:,
由得,∴,
∵为重心,∴,
∵点在椭圆上,故有,可得,
而,
点到直线的距离(是原点到距离的3倍得到),
∴,
当直线斜率不存在时,,,,∴的面积为定值.
21.【解析】(1)当时,有.
∵,∴,
∴过点的切线方程为:,即.
(2)当时,有,其定义域为:,
从而方程可化为:,
令,则,
由或;.
∴在和上单调递增,在上单调递减,
且,又当时,;当时,.
∵关于的方程有唯一实数解,∴实数的取值范围是:或.
(3)∵的定义域为:.
令. 又∵函数有两个极值点,
∴有两个不等实数根,
∴,且,从而.
由不等式恒成立恒成立,
∵,
令,∴,当时恒成立,
∴函数在上单调递减,∴,
故实数的取值范围是:.
22.(1)曲线的普通方程为,
则的极坐标方程为,
由于直线过原点,且倾斜角为,故其极坐标为(或)
(2)由得:,故,,
∴.
23(1) 解集为或;(2) .
(1)当时, 解得.
当时, 无解, 当时, 解得.
∴的解集为或.
(2)由已知恒成立. ∴恒成立.
又 . ∴,解得.
∴时,不等式恒成立