状元之路2015高考数学人教A版文一轮开卷速查57解三角形应用举例

状元之路2015高考数学人教A版文一轮开卷速查57解三角形应用举例

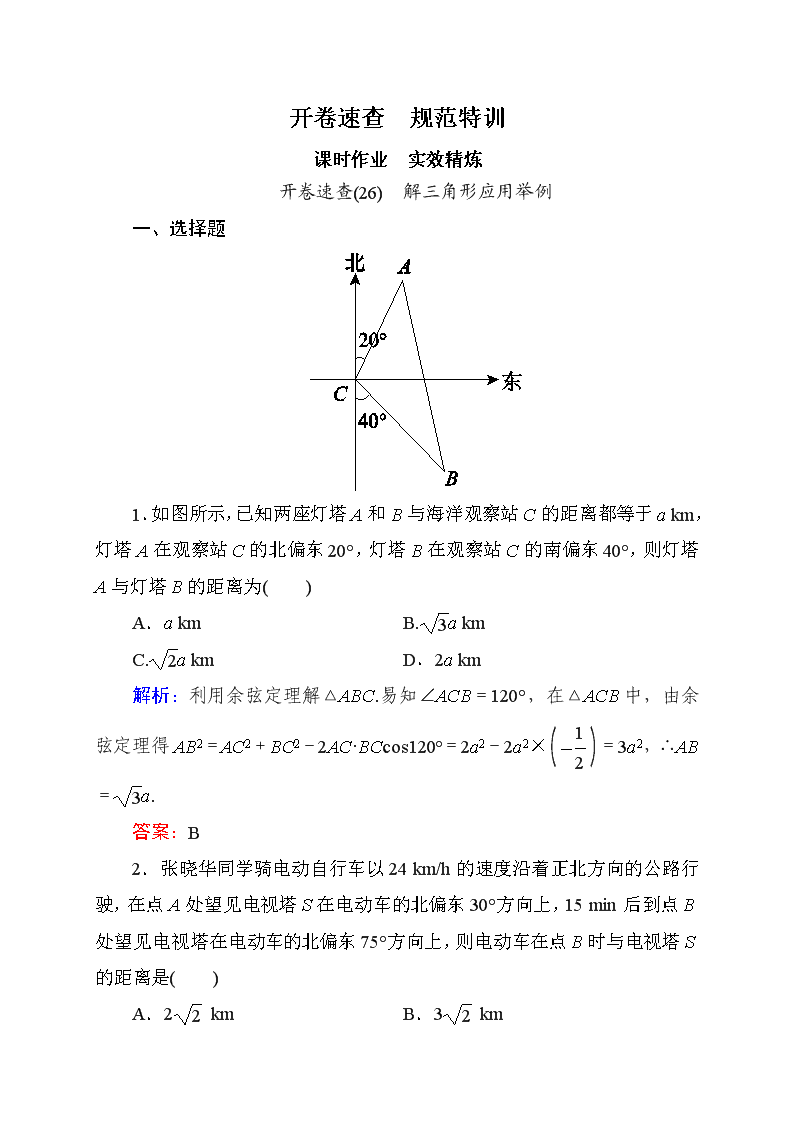
开卷速查　规范特训 课时作业　实效精炼 开卷速查(26)　解三角形应用举例 一、选择题 ‎1．如图所示，已知两座灯塔A和B与海洋观察站C的距离都等于a km，灯塔A在观察站C的北偏东20°，灯塔B在观察站C的南偏东40°，则灯塔A与灯塔B的距离为(　　)‎ A．a km　　　　　　　 B.a km C.a km D．‎2a km 解析：利用余弦定理解△ABC.易知∠ACB＝120°，在△ACB中，由余弦定理得AB2＝AC2＋BC2－‎2AC·BCcos120°＝‎2a2－‎2a2×＝‎3a2，∴AB＝a.‎ 答案：B ‎2．张晓华同学骑电动自行车以‎24 km/h的速度沿着正北方向的公路行驶，在点A处望见电视塔S在电动车的北偏东30°方向上，15 min后到点B处望见电视塔在电动车的北偏东75°方向上，则电动车在点B时与电视塔S的距离是(　　)‎ A．‎2 km B．‎3 km C．‎3 km D．‎2 km 解析：如图，由条件知AB＝24×＝6，在△ABS中，∠BAS＝30°，AB＝6，∠ABS＝180°－75°＝105°，所以∠ASB＝45°.由正弦定理知＝，‎ 所以BS＝sin30°＝3.‎ 答案：B ‎3．轮船A和轮船B在中午12时离开海港C，两艘轮船航行方向的夹角为120°，轮船A的航行速度是25海里/小时，轮船B的航行速度是15海里/小时，下午2时两船之间的距离是(　　)‎ A．35海里 B．35海里 C．35海里 D．70海里 解析：设轮船A、B航行到下午2时时所在的位置分别是E、F，则依题意有CE＝25×2＝50，CF＝15×2＝30，且∠ECF＝120°，‎ EF＝ ‎＝ ‎＝70.‎ 答案：D ‎4．为测量某塔AB的高度，在一幢与塔AB相距‎20 m 的楼的楼顶处测得塔顶A的仰角为30°，测得塔基B的俯角为45°，那么塔AB的高度是(　　)‎ A．‎20 m B．‎20 m C．20(1＋) m D．‎‎30 m 解析：如图所示，由已知可知，四边形CBMD为正方形，CB＝‎20 m，所以BM＝‎20 m．又在Rt△AMD中，‎ DM＝‎20 m，∠ADM＝30°，‎ ‎∴AM＝DMtan30°＝(m)．‎ ‎∴AB＝AM＋MB＝＋20‎ ‎＝20(m)．‎ 答案：A ‎5．线段AB外有一点C，∠ABC＝60°，AB＝‎200 km，汽车以‎80 km/h的速度由A向B行驶，同时摩托车以‎50 km/h的速度由B向C行驶，则运动开始多少h后，两车的距离最小(　　)‎ A. B．1‎ C. D．2‎ 解析：如图所示，设t h后，汽车由A行驶到D，摩托车由B行驶到E，则AD＝80t，BE＝50t.因为AB＝200，所以BD＝200－80t，问题就是求DE最小时t的值．‎ 由余弦定理，得 DE2＝BD2＋BE2－2BD·BEcos60°‎ ‎＝(200－80t)2＋2 500t2－(200－80t)·50t ‎＝12 900t2－42 000t＋40 000.‎ 当t＝时，DE最小. ‎ 答案：C ‎6．已知A船在灯塔C北偏东80°处，且A船到灯塔C的距离为‎2 km，B船在灯塔C北偏西40°处，A，B两船间的距离为‎3 km，则B船到灯塔C的距离为(　　)‎ A．‎1 km B．‎‎2 km C．‎3 km D．(－1) km 解析：如图，由题意可得，∠ACB＝120°，AC＝2，AB＝3.‎ 设BC＝x，则由余弦定理可得 AB2＝BC2＋AC2－2BC·ACcos120°，‎ 即32＝22＋x2－2×2xcos120°，整理得x2＋2x＝5，‎ 解得x＝－1(负值舍掉)．‎ 答案：D ‎7．一个大型喷水池的中央有一个强力喷水柱，为了测量喷水柱喷出的水柱的高度，某人在喷水柱正西方向的点A测得水柱顶端的仰角为45°，沿点A向北偏东30°前进‎100 m到达点B，在B点测得水柱顶端的仰角为30°，则水柱的高度是(　　)‎ A．‎50 m B．‎‎100 m C．‎120 m D．‎‎150 m 解析：设水柱高度是h m，水柱底端为C，则在△ABC中，∠A＝60°，AC＝h，AB＝100，BC＝h，根据余弦定理得，(h)2＝h2＋1002－2·h·100·cos60°，即h2＋50h－5 000＝0，即(h－50)(h＋100)＝0，即h＝50，故水柱的高度是‎50 m.‎ 答案：A ‎8．如图所示，在某点B处测得建筑物AE的顶端A的仰角为θ，沿BE方向前进‎30米至C处，测得其顶端A的仰角为2θ，再继续前进‎10‎米至 D处，测得其顶端A的仰角为4θ，则θ的值为(　　)‎ A．15° B．10°‎ C．5° D．20°‎ 解析：因为∠ACE＝2θ，所以∠BAC＝θ，AC＝BC＝30，因为∠ADE＝4θ，所以∠CAD＝2θ，所以AD＝CD＝10，在△ACD中，2CD·cos2θ＝AC，所以cos2θ＝＝＝，所以2θ＝30°，所以θ＝15°.‎ 答案：A ‎9．某人向正东方向走x km后，向右转150°，然后朝新方向走‎3 km，结果他离出发点恰好是 km，那么x的值为(　　)‎ A. B．2 C.或2 D．3‎ 解析：如图所示，设此人从A出发，则AB＝x，BC＝3，AC＝，∠ABC＝30°，由余弦定理得()2＝x2＋32－2x·3·cos30°，整理，得x2－3x＋6＝0，解得x＝或2.‎ 答案：C ‎10．一艘海轮从A处出发，以每小时40海里的速度沿南偏东40°的方向直线航行，30分钟后到达B处，在C处有一座灯塔，海轮在A处观察灯塔，其方向是南偏东70°，在B处观察灯塔，其方向是北偏东65°，那么B，C两点间的距离是(　　)‎ A．10海里 B．10海里 C．20海里 D．20海里 解析：如图，易知，在△ABC中，AB＝20，∠CAB＝30°，∠ACB＝45°，根据正弦定理得＝，‎ 解得BC＝10(海里)．‎ 答案：A 二、填空题 ‎11．一船由B处向正北方向航行，看见正西方向有相距10海里的两个灯塔C、D恰好与它在一条直线上，继续航行半小时后到达A处，看见灯塔C在它的南偏西60°方向，灯塔D在它的南偏西75°方向，则这艘船的速度是__________海里/小时．‎ 解析：如图所示，‎ 依题意有∠BAC＝60°，∠BAD＝75°，所以∠CAD＝∠CDA＝15°，从而CD＝CA＝10，在直角三角形ABC中，得AB＝5，于是这艘船的速度是＝10(海里/小时)．‎ 答案：10‎ ‎12．某路边一树干被大风吹断后，折成与地面成45°角，树干也倾斜为与地面成75°角，树干底部与树尖着地处相距‎20米，则折断点与树干底部的距离是__________米．‎ 解析：如图，设树干底部为O，树尖着地处为B，折断点为A，则∠ABO＝45°，∠AOB＝75°，‎ ‎∴∠OAB＝60°.‎ 由正弦定理知，＝，‎ ‎∴AO＝(米)．‎ 答案： ‎13．在直径为‎30 m的圆形广场中央上空，设置一个照明光源，射向地面的光呈圆形，且其轴截面顶角为120°，若要光源恰好照整个广场，则光源的高度为__________m.‎ 解析：轴截面如图，则光源高度h＝＝5(m)．‎ 答案：5 ‎14．在O 点测量到远处有一物体在做匀速直线运动，开始时刻物体位于P点，一分钟后，其位置在Q点，且∠POQ＝90°，再过一分钟，该物体位于R点，且∠QOR＝30°，则tan∠OPQ的值为__________．‎ 解析：由于物体做匀速直线运动，根据题意，PQ＝QR，不妨设其长度为1.在Rt△POQ中，OQ＝sin∠OPQ，OP＝cos∠OPQ，在△OPR中，由正弦定理得＝，在△ORP中，＝，两式两边同时相除得＝tan∠OPQ＝.‎ 答案： 三、解答题 ‎15．某城市有一块不规则的绿地如图所示，城建部门欲在该地上建造一个底座为三角形的环境标志，小李、小王设计的底座形状分别为△ABC、△ABD，经测量AD＝BD＝14，BC＝10，AC＝16，∠C＝∠D.‎ ‎(1)求AB的长度；‎ ‎(2)若建造环境标志的费用与用地面积成正比，不考虑其他因素，小李、小王谁的设计建造费用最低？请说明理由．‎ 解析：(1)在△ABC中，由余弦定理，得AB2＝AC2＋BC2－‎2AC·BCcosC＝162＋102－2×16×10cosC，①‎ 在△ABD中，由余弦定理及∠C＝∠D，整理得AB2＝AD2＋BD2‎ ‎－2AD·BDcosD＝142＋142－2×142cosC.②‎ 由①②得：142＋142－2×142cosC＝162＋102－2×16×10×cosC，整理得cosC＝.‎ ‎∵∠C为三角形的内角，∴C＝60°，‎ 又∠C＝∠D，AD＝BD，‎ ‎∴ABD是等边三角形，‎ 故AB＝14，即A、B两点的距离为14.‎ ‎(2)小李的设计使建造费用最低．‎ 理由如下：‎ S△ABD＝AD·BDsinD，‎ S△ABC＝AC·BCsinC.‎ ‎∵AD·BD＞AC·BC，且sinD＝sinC，‎ ‎∴S△ABD＞S△ABC.‎ 由已知建造费用与用地面积成正比，故选择小李的设计使建造费用最低．‎ 答案：(1)14；(2)小李的设计建造费用最低，理由略．‎ ‎16．[2013·江苏]如图，游客从某旅游景区的景点A处下山至C处有两种路径．一种是从A沿直线步行到C，另一种是先从A沿索道乘缆车到B，然后从B沿直线步行到C.‎ 现有甲、乙两位游客从A处下山，甲沿AC匀速步行，速度为‎50 m/min，在甲出发2 min后，乙从A乘缆车到B，在B处停留1 min后，再从B匀速步行到C，假设缆车匀速直线运动的速度为‎130 m/min，山路AC长为1 ‎260 m，经测量，cosA＝，cosC＝.‎ ‎(1)求索道AB的长；‎ ‎(2)问乙出发多少分钟后，乙在缆车上与甲的距离最短？‎ ‎(3)为使两位游客在C处互相等待的时间不超过3分钟，乙步行的速度应控制在什么范围内？‎ 解析：(1)在△ABC中，因为cosA＝，‎ cosC＝，所以sinA＝，sinC＝.‎ 从而sinB＝sin[π－(A＋C)]＝sin(A＋C)‎ ‎＝sinAcosC＋cosAsinC ‎＝×＋×＝.‎ 由正弦定理＝，得 AB＝×sinC＝×＝1 040(m)．‎ 所以索道AB的长为1 ‎040 m.‎ ‎(2)假设乙出发t min后，甲、乙两游客距离为d，此时，甲行走了(100＋50t) m，乙距离A处130t m，所以由余弦定理得 d2＝(100＋50t)2＋(130t)2－2×130t×(100＋50t)×＝200(37t2－70t＋50)，‎ 因0≤t≤，即0≤t≤8，故当t＝(min)时，甲、乙两游客距离最短．‎ ‎(3)由正弦定理＝，得 BC＝×sinA＝×＝500(m)．‎ 乙从B出发时，甲已走了50×(2＋8＋1)＝550(m)，还需走‎710 m才能到达C.‎ 设乙步行的速度为v m/min，由题意得－3≤－≤3，解得≤v≤，所以为使两位游客在C处互相等待的时间不超过3 min，乙步行的速度应控制在(单位：m/min)范围内．‎ 答案：(1)1 ‎040 m；(2) (min)；(3)应控制在(单位：m/min)范围内．‎ 创新试题　教师备选 教学积累　资源共享 教师用书独具 ‎1．[2014·台州模拟]某校运动会开幕式上举行升旗仪式，旗杆正好处于坡度15°的看台的某一列的正前方，从这一列的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°，第一排和最后一排的距离为‎10‎米(如图所示)，旗杆底部与第一排在一个水平面上．若国歌长度约为50秒，升旗手应以多大的速度匀速升旗？‎ 解析：在△BCD中，∠BDC＝45°，∠CBD＝30°，CD＝10，由正弦定理，得BC＝＝20.‎ 在Rt△ABC中，AB＝BCsin60°＝20×＝30(米)，所以升旗速度v＝＝＝0.6(米/秒)．‎ ‎2．如图，A、B是海面上位于东西方向相距5(3＋)海里的两个观测点，现位于A点北偏东45°，B点北偏西60°的D 点有一艘轮船发出求救信号，位于B点南偏西60°且与B点相距20海里的C点的救援船立即前往营救，其航行速度为30海里/时，该救援船到达D点需要多长时间？‎ 解析：由题意，知AB＝5(3＋)海里，∠DBA＝90°－60°＝30°，∠DAB＝90°－45°＝45°，‎ ‎∴∠ADB＝180°－(45°＋30°)＝105°.‎ 在△DAB中，由正弦定理，得 ＝，‎ 于是DB＝ ‎＝ ‎＝ ‎＝ ‎＝10(海里)．‎ 又∠DBC＝∠DBA＋∠ABC＝30°＋(90°－60°)＝60°，‎ BC＝20(海里)，‎ 在△DBC中，由余弦定理，得 CD2＝BD2＋BC2－2BD·BC·cos∠DBC ‎＝300＋1 200－2×10×20× ‎＝900.‎ 得CD＝30(海里)，故需要的时间t＝＝1(小时)，‎ 即救援船到达D点需要1小时．‎ ‎3．如图所示，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个测点C与D，现测得∠BCD＝α，∠BDC＝β，CD＝s，并在点C测得塔顶A的仰角为θ，求塔高AB.‎ 解析：在△BCD中，∠CBD＝π－α－β，‎ 由正弦定理得＝，‎ 所以BC＝＝ 在Rt△ABC中，AB＝BCtan∠ACB＝