- 2021-04-22 发布 |
- 37.5 KB |
- 5页
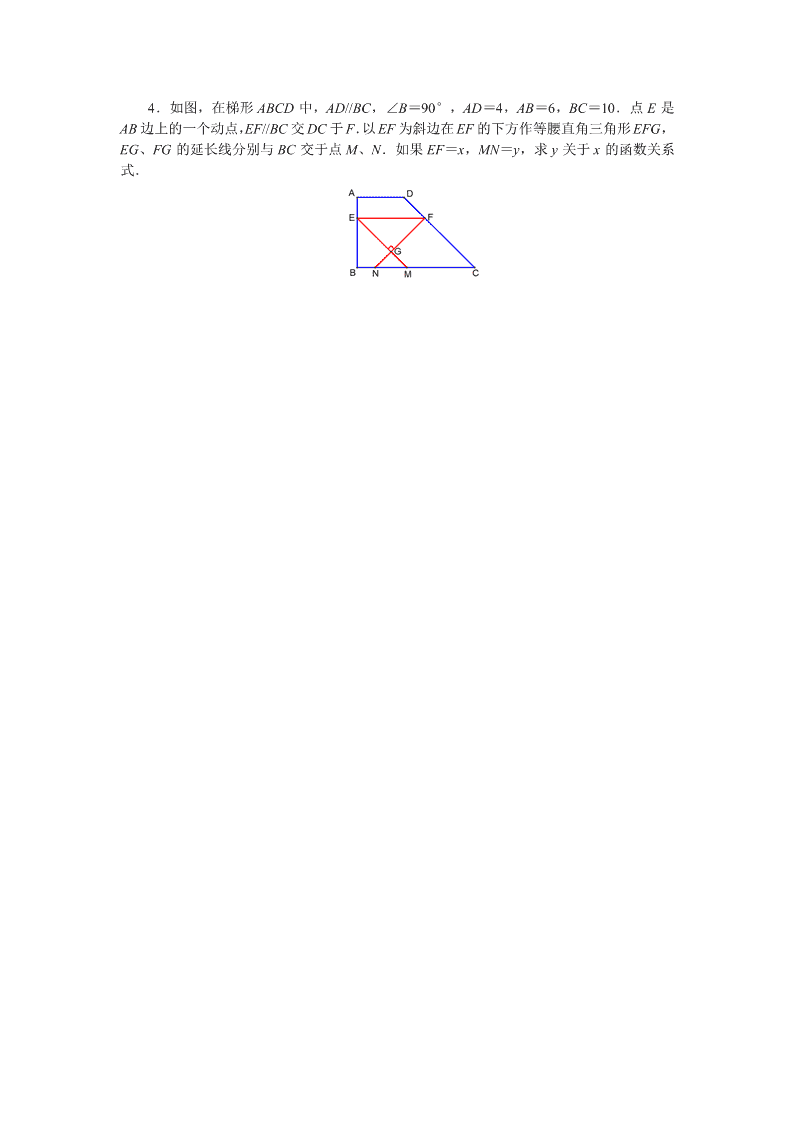
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学压轴题5
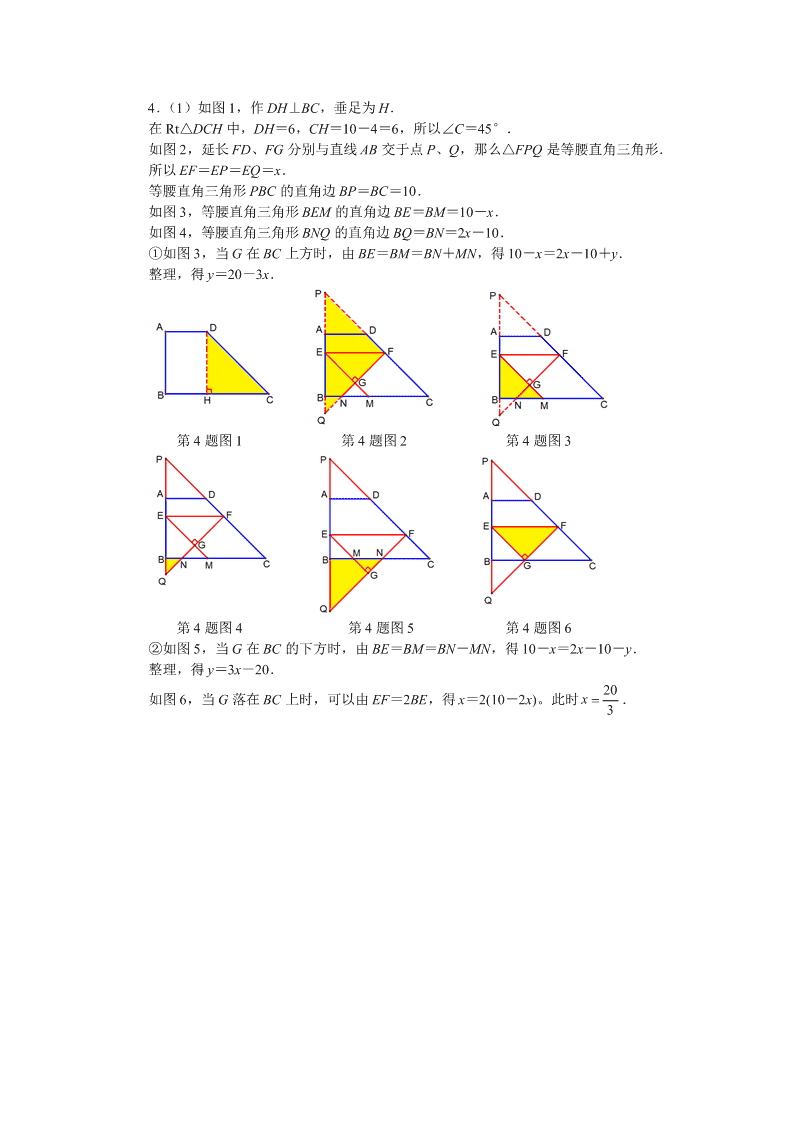
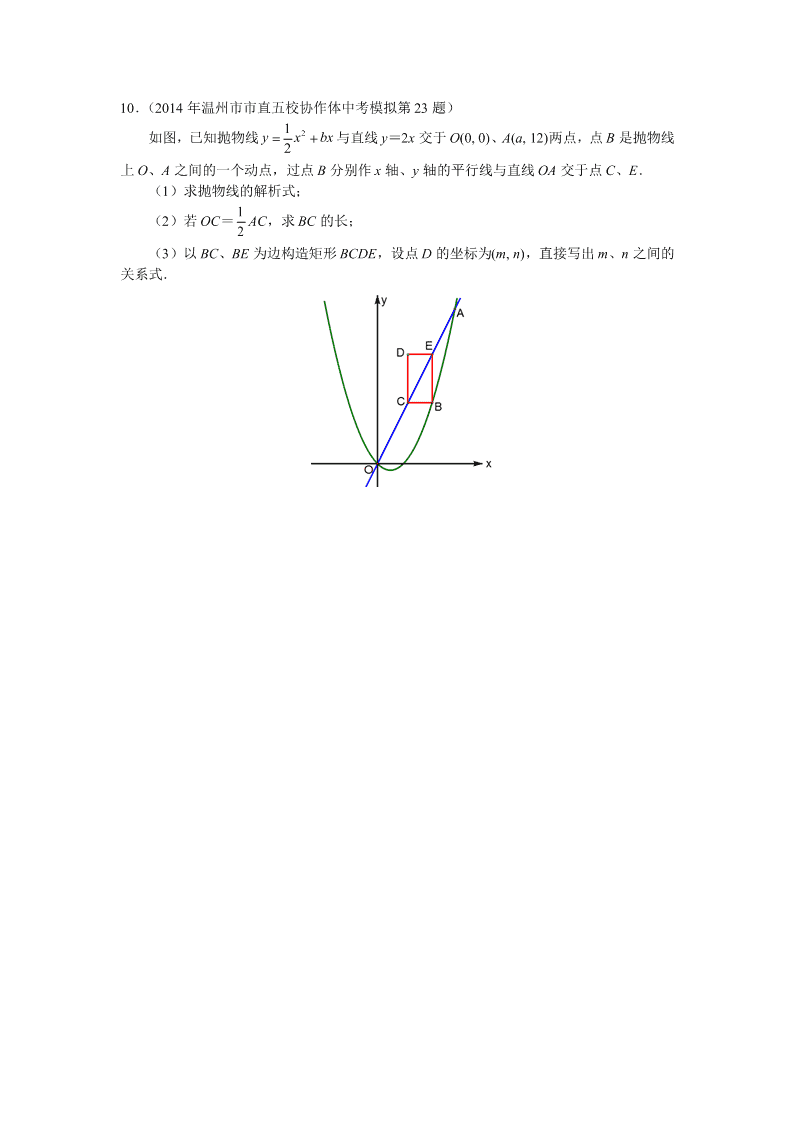
4.如图,在梯形 ABCD 中,AD//BC,∠B=90°,AD=4,AB=6,BC=10.点 E 是 AB 边上的一个动点,EF//BC 交 DC 于 F.以 EF 为斜边在 EF 的下方作等腰直角三角形 EFG, EG、FG 的延长线分别与 BC 交于点 M、N.如果 EF=x,MN=y,求 y 关于 x 的函数关系 式. 4.(1)如图 1,作 DH⊥BC,垂足为 H. 在 Rt△DCH 中,DH=6,CH=10-4=6,所以∠C=45°. 如图 2,延长 FD、FG 分别与直线 AB 交于点 P、Q,那么△FPQ 是等腰直角三角形. 所以 EF=EP=EQ=x. 等腰直角三角形 PBC 的直角边 BP=BC=10. 如图 3,等腰直角三角形 BEM 的直角边 BE=BM=10-x. 如图 4,等腰直角三角形 BNQ 的直角边 BQ=BN=2x-10. ①如图 3,当 G 在 BC 上方时,由 BE=BM=BN+MN,得 10-x=2x-10+y. 整理,得 y=20-3x. 第 4 题图 1 第 4 题图 2 第 4 题图 3 第 4 题图 4 第 4 题图 5 第 4 题图 6 ②如图 5,当 G 在 BC 的下方时,由 BE=BM=BN-MN,得 10-x=2x-10-y. 整理,得 y=3x-20. 如图 6,当 G 落在 BC 上时,可以由 EF=2BE,得 x=2(10-2x)。此时 20 3x . 10.( 2014 年温州市市直五校协作体中考模拟第 23 题) 如图,已知抛物线 21 2y x bx与直线 y=2x 交于 O(0, 0)、A(a, 12)两点,点 B 是抛物线 上 O、A 之间的一个动点,过点 B 分别作 x 轴、y 轴的平行线与直线 OA 交于点 C、E. (1)求抛物线的解析式; (2)若 OC= 1 2 AC,求 BC 的长; (3)以 BC、BE 为边构造矩形 BCDE,设点 D 的坐标为(m, n),直接写出 m、n 之间的 关系式. 10.(1)将 A(a, 12)代入 y=2x,得 a=6.所以 A(6, 12). 将 A(6, 12)代入 21 2y x bx,得 12=18+6b.解得 b=-1. 所以抛物线的解析式是 21 2y x x. (2)由 O(0, 0)、A(6, 12),可知 O、A 间的水平距离为 6,垂直距离为 12. 当 OC= 1 2 AC 时,点 C 的坐标为(2, 4). 解方程 21 42 xx,得 x=4,或 x=-2. 所以点 B 的坐标为(2, 4).此时 BC=2. (3)如图 1,已知 D(m, n),由于 DE//x 轴,E 在直线 y=2x 上,所以 E 1( , )2 nn . 由于 DC//y 轴,C 在直线 y=2x 上,所以 C(m, 2m). 所以点 B 的坐标为 1( ,2 )2 nm,代入 ,得 21 1 12 ( )2 2 2m n n . 于是得到 m、n 之间的关系式是 211 16 4m n n. 第 10 题图 1 4.如图,在△ABC 中,AB=AC=10, 5 3cos B ,点 D 在 AB 边上(点 D 与点 A,B 不重合),DE∥BC 交 AC 边于点 E,点 F 在线段 EC 上,且 AEEF 4 1 ,以 DE、EF 为邻边 作平行四边形 DEFG,联结 BG. (1)当 EF=FC 时,求△ADE 的面积; (2)设 AE=x,△DBG 的面积为 y,求 y 与 x 的函数关系式,并写出 x 的取值范围. 4.( 1)如图 1,作 AH⊥BC,垂足为 M,分别交 DE、GF 于 M、N. 在 Rt△ABM 中,AB=10, 5 3cos B ,所以 BM=6,AM=8,BC=12. 所以 1 482ABCS BC AM △ . 设 AE=x,当 EF=FC 时, 151044xx .解得 20 3x . 因为 DE//BC,所以 2 ADE ABC S AE S AC △ △ .所以 222 644833ADE ABC AESSAC △ △ . (2)【解法一】如图 1,在 Rt△AEM 中,AE=x,所以 4 5AM x , 3 5EM x . 所以 62 5DE GF EM x , 11 45MN AM x, 8NH x. 于是 S△ADE= 21 6 4 12 2 5 5 25x x x , S 平行四边形 DEFG= 26 1 6 5 5 25x x x , S 梯形 BCFG= 21 6 3 6( 12)(8 ) 482 5 5 5x x x x . 因此 y=S△BDG= 2 2 212 6 3 648 ( ) ( ) ( 48)25 25 5 5x x x x 236 25 5xx . x 的取值范围是 0<x≤8. 【解法二】如图 2,延长 DG 交 BC 于 Q,那么△DBQ∽△ABC. 所以 S△DBQ∶S△ABC=DB2∶AB2.因此 S△DBQ∶48=(10-x)2∶102. 所以 S△DBQ= 212 (10 )25 x . 又因为△BDG 与△BDQ 是同高三角形,所以 S△BDG∶S△BDQ=DG∶DQ. 所以 212: (10 )25yx 1 :(10 )4 xx.于是得到 236 25 5y x x . 第 4 题图 1 第 4 题图 2查看更多