2020九年级数学下册 第2章圆周角

2020九年级数学下册 第2章圆周角

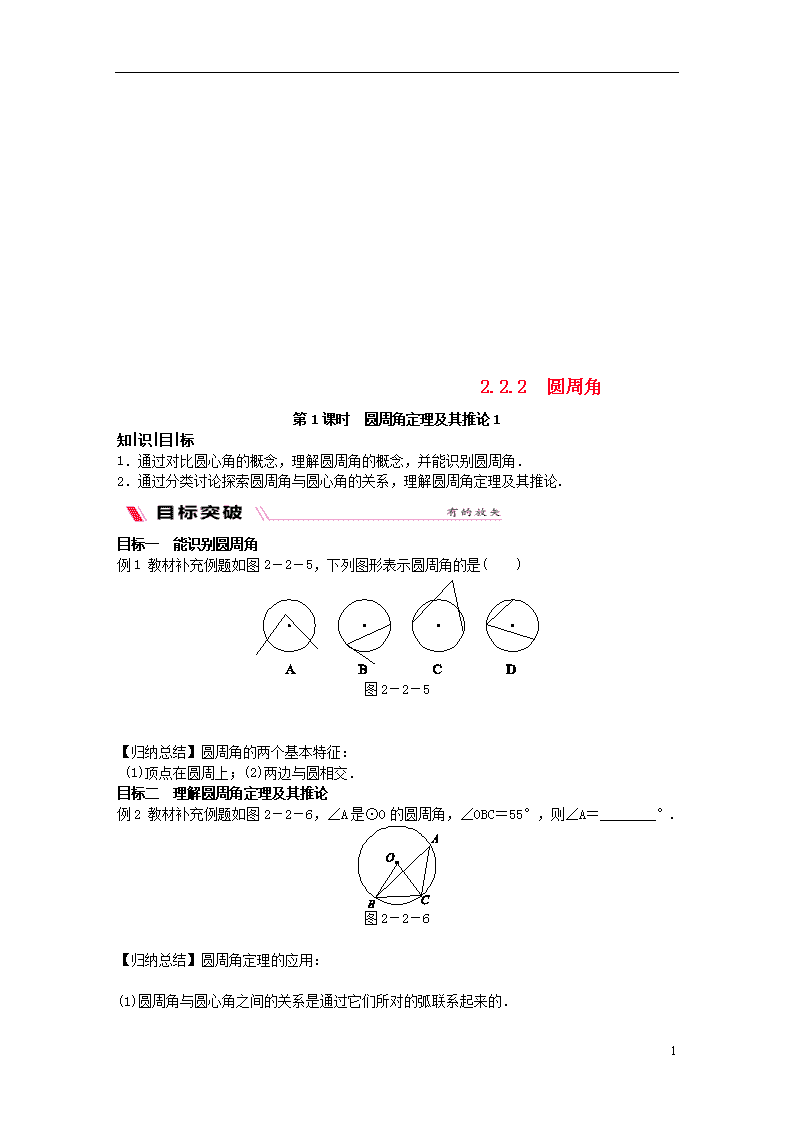
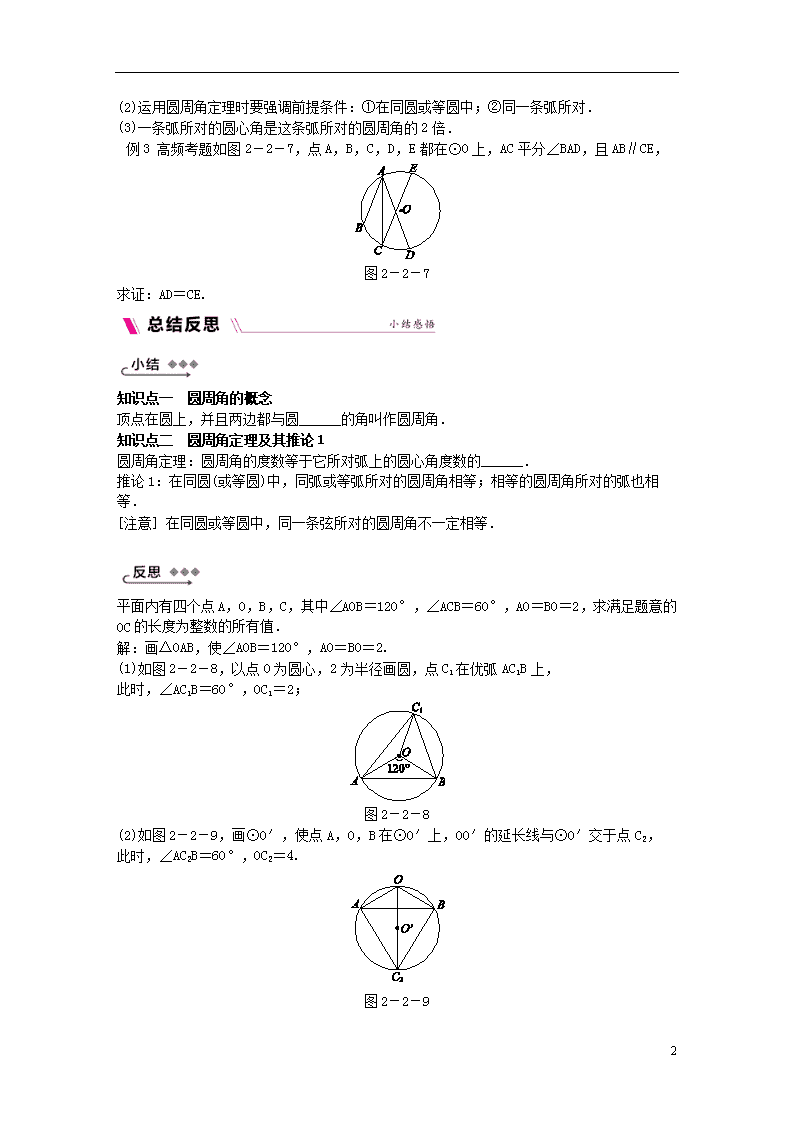
‎2.2.2　‎圆周角 第1课时　圆周角定理及其推论1‎ 知|识|目|标 ‎1．通过对比圆心角的概念，理解圆周角的概念，并能识别圆周角．‎ ‎2．通过分类讨论探索圆周角与圆心角的关系，理解圆周角定理及其推论.‎ 目标一　能识别圆周角 例1 教材补充例题如图2－2－5，下列图形表示圆周角的是(　　)‎ 图2－2－5‎ ‎【归纳总结】圆周角的两个基本特征：‎ ‎ (1)顶点在圆周上；(2)两边与圆相交．‎ 目标二　理解圆周角定理及其推论 例2 教材补充例题如图2－2－6，∠A是⊙O的圆周角，∠OBC＝55°，则∠A＝________°.‎ 图2－2－6‎ ‎【归纳总结】圆周角定理的应用：‎ ‎(1)圆周角与圆心角之间的关系是通过它们所对的弧联系起来的．‎ 4‎ ‎(2)运用圆周角定理时要强调前提条件：①在同圆或等圆中；②同一条弧所对．‎ ‎(3)一条弧所对的圆心角是这条弧所对的圆周角的2倍．‎ 例3 高频考题如图2－2－7，点A，B，C，D，E都在⊙O上，AC平分∠BAD，且AB∥CE， ‎ 图2－2－7‎ 求证：AD＝CE.‎ 知识点一　圆周角的概念 顶点在圆上，并且两边都与圆______的角叫作圆周角．‎ 知识点二　圆周角定理及其推论1‎ 圆周角定理：圆周角的度数等于它所对弧上的圆心角度数的______．‎ 推论1：在同圆(或等圆)中，同弧或等弧所对的圆周角相等；相等的圆周角所对的弧也相等．‎ ‎[注意] 在同圆或等圆中，同一条弦所对的圆周角不一定相等．‎ ‎　‎ 平面内有四个点A，O，B，C，其中∠AOB＝120°，∠ACB＝60°，AO＝BO＝2，求满足题意的OC的长度为整数的所有值．‎ 解：画△OAB，使∠AOB＝120°，AO＝BO＝2.‎ ‎(1)如图2－2－8，以点O为圆心，2为半径画圆，点C1在优弧AC1B上，‎ 此时，∠AC1B＝60°，OC1＝2；‎ 图2－2－8‎ ‎(2)如图2－2－9，画⊙O′，使点A，O，B在⊙O′上，OO′的延长线与⊙O′交于点C2，‎ 此时，∠AC2B＝60°，OC2＝4.‎ 图2－2－9‎ 4‎ 所以OC的长度为整数的所有值是2，4.‎ 以上解答完整吗？若不完整，请进行补充．‎ 4‎ 教师详解详析 ‎【目标突破】‎ 例1　D 例2　[答案] 35‎ ‎[解析] ∵OB＝OC，∠OBC＝55°，∴∠OCB＝55°，∴∠BOC＝180°－55°－55°＝70°，由圆周角定理得∠A＝∠BOC＝35°.‎ 例3　证明：∵AB∥CE，‎ ‎∴∠ACE＝∠BAC.‎ 又∵AC平分∠BAD，‎ ‎∴∠BAC＝∠DAC，‎ ‎∴∠ACE＝∠CAD，∴＝，‎ ‎∴＋＝＋，‎ ‎∴＝，∴AD＝CE.‎ ‎【总结反思】‎ ‎[小结] ‎ 知识点一　相交 知识点二　一半 ‎[反思] 不完整．补充如下：‎ 在题图2－2－9中，以点O为圆心，3为半径画弧与⊙O′交于点C3，如图所示，此时，∠AC3B＝60°，OC3＝3，所以OC的长度为整数的所有值是2，3，4.‎ 度数)．‎ 4‎