- 2021-04-21 发布 |
- 37.5 KB |
- 43页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020全国中考数学试卷分类汇编(2)专题26 图形的相似与位似
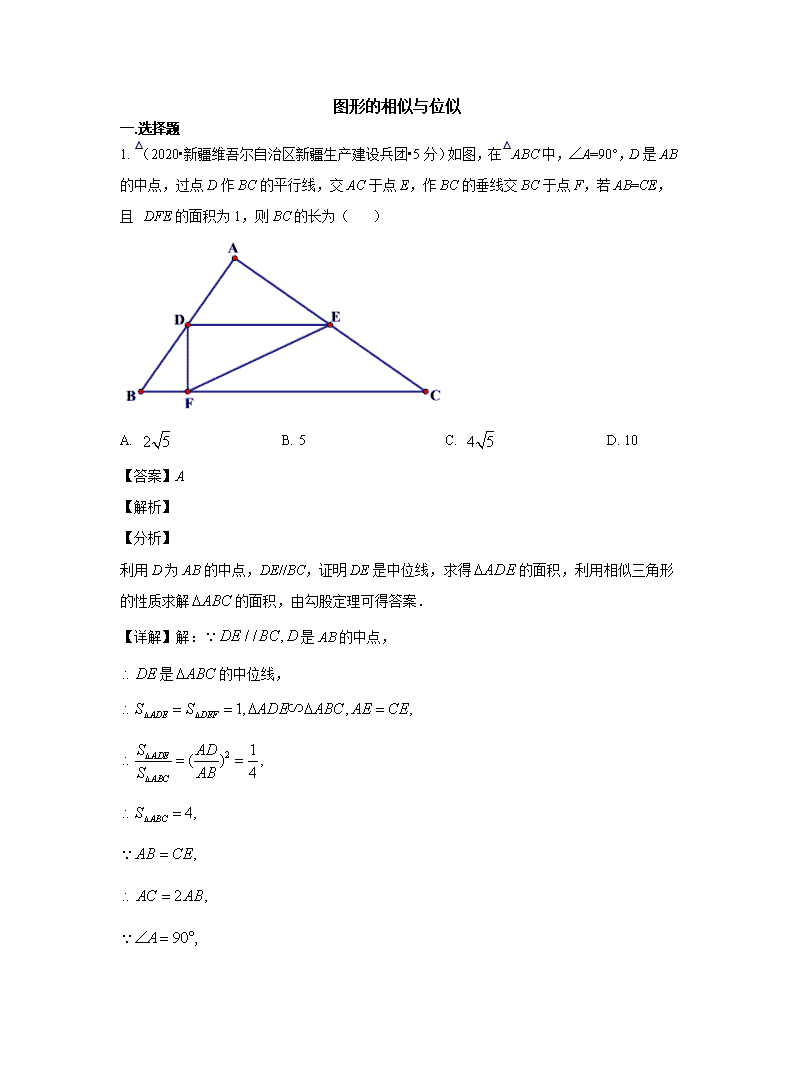
图形的相似与位似 一.选择题 1. (2020•新疆维吾尔自治区新疆生产建设兵团•5分)如图,在△ABC中,∠A=90°,D是AB的中点,过点D作BC的平行线,交AC于点E,作BC的垂线交BC于点F,若AB=CE,且△DFE的面积为1,则BC的长为( ) A. B. 5 C. D. 10 【答案】A 【解析】 【分析】 利用D为AB的中点,DE//BC,证明DE是中位线,求得的面积,利用相似三角形的性质求解的面积,由勾股定理可得答案. 【详解】解:是AB的中点, 是的中位线, 故选A. 【点睛】本题考查了三角形的中位线的性质,相似三角形的判定与性质,勾股定理的应用,掌握以上知识是解题的关键. 2.(2020•内蒙古包头市•3分)如图,在平面直角坐标系中,直线与x轴、y轴分别交于点A和点是线段上一点,过点C作轴,垂足为D,轴,垂足为E,.若双曲线经过点C,则k的值为( ) A. B. C. D. 【答案】A 【解析】 【分析】 由直线求出OA,OB的长,设出C(x,),证明,得出CE,CD的长,进而得出结论. 【详解】解:对于,当时,;当时,, , , 设, 根据题意知,四边形ODCE是矩形, , 轴,轴, , , , , , 解得: 经检验,是原方程的根, ∵点C在反比例函数的图象上, ,即, 故选:A. 【点睛】本题考查了反比例函数综合,用到的知识点是相似三角形的判定与性质以及待定系数法求函数的解析式等,难度适中,正确求得C的坐标是关键,注意掌握数形结合思想与方程思想的应用. 3.(2020•辽宁省营口市•3分)如图,在△ABC中,DE∥AB,且=,则的值为( ) A. B. C. D. 【分析】平行于三角形一边的直线截其他两边所得的对应线段成比例,据此可得结论. 【解答】解:∵DE∥AB, ∴==, ∴的值为, 故选:A. 4. (2020•山东省潍坊市•3分)如图,点E是□ABCD的边AD上的一点,且,连接BE并延长交CD的延长线于点F,若DE=3,DF=4,则□ABCD的周长为( ) A.21 B.28 C.34 D.42 【分析】根据平行四边形的性质得AB∥CD,再由平行线得相似三角形,根据相似三角形求得AB,AE,进而根据平行四边形的周长公式求得结果. 【解答】解:∵四边形ABCD是平行四边形,∴AB∥CF,AB=CD,∴△ABE∽△DFE, ∴,∵DE=3,DF=4,∴AE=6,AB=8,∴AD=AE+DE=6+3=9, ∴平行四边形ABCD的周长为:(8+9)×2=34.故选C. 【点评】此题考查相似三角形的判定和性质,关键是根据平行四边形的性质和相似三角形的判定和性质解答 5.(2020•广东省广州市•3分)如图,矩形的对角线,交于点,,,过点作,交于点,过点作,垂足为,则的值为( ) A. B. C. D. 【答案】C 【解析】 【分析】 根据勾股定理求出AC=BD=10,由矩形的性质得出AO=5,证明得到OE的长,再证明可得到EF的长,从而可得到结论. 【详解】∵四边形ABCD是矩形, , , , ,, , , , 又, , , , ,, , 同理可证,, , , , , 故选:C. 【点睛】本题主要考查了矩形的性质和相似三角形的判定与性质,熟练掌握判定与性质是解答此题的关键. 6.(2020•广西省玉林市•3分)一个三角形木架三边长分别是75cm,100cm,120cm,现要再做一个与其相似的三角形木架,而只有长为60cm和120cm的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有( ) A.一种 B.两种 C.三种 D.四种 【分析】分类讨论:长120cm的木条与三角形木架的最长边相等,则长120cm的木条不能作为一边,设从120cm的一根上截下的两段长分别为xcm,ycm(x+y≤120),易得长60cm的木条不能与75cm的一边对应,所以当长60cm的木条与100cm的一边对应时有==;当长60cm的木条与120cm的一边对应时有==,然后分别利用比例的性质计算出两种情况下得x和y的值. 【解答】解:长120cm 的木条与三角形木架的最长边相等,要满足两边之和大于第三边,则长120cm的木条不能作为一边, 设从120cm的木条上截下两段长分别为xcm,ycm(x+y≤120), 由于长60cm的木条不能与75cm的一边对应,否则x、y有大于120cm, 当长60cm的木条与100cm的一边对应,则==, 解得:x=45,y=72; 当长60cm的木条与120cm的一边对应,则==, 解得:x=37.5,y=50. 答:有两种不同的截法:把120cm的木条截成45cm、72cm两段或把120cm的木条截成37.5cm、50cm两段. 故选:B. 【点评】本题考查了相似三角形的应用:通常构建三角形相似,然后利用相似三角形的性质即相似三角形的对应边的比相等进行几何计算. 7. (2020•甘肃省天水市•4分)如图所示,某校数学兴趣小组利用标杆测量建筑物的高度,已知标杆高,测得,,则建筑物的高是( ) A. B. C. D. 【答案】A 【解析】 【分析】 先求得AC,再说明△ABE∽△ACD,最后根据相似三角形的性质列方程解答即可. 【详解】解:∵, ∴AC=1.2m+12.8m=14m ∵标杆和建筑物CD均垂直于地面 ∴BE//CD ∴△ABE∽△ACD ∴,即,解得CD=17.5m. 故答案为A. 【点睛】本题考查了相似三角形的应用,正确判定相似三角形并利用相似三角形的性质列方程计算是解答本题的关键. 8.(2020•福建省•4分)如图,面积为1的等边三角形ABC中,D,E,F分别是AB,BC,CA的中点,则△DEF的面积是( ) A.1 B. C. D. 【分析】根据三角形的中位线定理和相似三角形的判定和性质定理即可得到结论. 【解答】解:∵D,E,F分别是AB,BC,CA的中点, ∴DE=AC,DF=BC,EF=AB, ∴=, ∴△DEF∽△ABC, ∴=()2=()2=, ∵等边三角形ABC的面积为1, ∴△DEF的面积是, 故选:D. 【点评】本题考查了三角形中位线定理,等边三角形的性质,相似三角形的判定和性质,熟练掌握三角形的中位线定理是解题的关键. 9. (2020•广东省广州市•3分)如图,矩形的对角线,交于点, ,,过点作,交于点,过点作,垂足为,则的值为( ) A. B. C. D. 【答案】C 【解析】 【分析】 根据勾股定理求出AC=BD=10,由矩形的性质得出AO=5,证明得到OE的长,再证明可得到EF的长,从而可得到结论. 【详解】∵四边形ABCD是矩形, , , , ,, , , , 又, , , , ,, , 同理可证,, , , , , 故选:C. 【点睛】本题主要考查了矩形的性质和相似三角形的判定与性质,熟练掌握判定与性质是解答此题的关键. 10.(2020•广西省玉林市•3分)一个三角形木架三边长分别是75cm,100cm,120cm,现要再做一个与其相似的三角形木架,而只有长为60cm和120cm的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有( ) A.一种 B.两种 C.三种 D.四种 【分析】分类讨论:长120cm的木条与三角形木架的最长边相等,则长120cm的木条不能作为一边,设从120cm的一根上截下的两段长分别为xcm,ycm(x+y≤120),易得长60cm的木条不能与75cm的一边对应,所以当长60cm的木条与100cm的一边对应时有==;当长60cm的木条与120cm的一边对应时有==,然后分别利用比例的性质计算出两种情况下得x和y的值. 【解答】解:长120cm的木条与三角形木架的最长边相等,要满足两边之和大于第三边,则长120cm的木条不能作为一边, 设从120cm的木条上截下两段长分别为xcm,ycm(x+y≤120), 由于长60cm的木条不能与75cm的一边对应,否则x、y有大于120cm, 当长60cm的木条与100cm的一边对应,则==, 解得:x=45,y=72; 当长60cm的木条与120cm的一边对应,则==, 解得:x=37.5,y=50. 答:有两种不同的截法:把120cm的木条截成45cm、72cm两段或把120cm的木条截成37.5cm、50cm两段. 故选:B. 【点评】本题考查了相似三角形的应用:通常构建三角形相似,然后利用相似三角形的性质即相似三角形的对应边的比相等进行几何计算. 11. (2020•甘肃省天水市•4分)如图所示,某校数学兴趣小组利用标杆测量建筑物的高度,已知标杆高,测得,,则建筑物的高是( ) A. B. C. D. 【答案】A 【解析】 【分析】 先求得AC,再说明△ABE∽△ACD,最后根据相似三角形的性质列方程解答即可. 【详解】解:∵, ∴AC=1.2m+12.8m=14m ∵标杆和建筑物CD均垂直于地面 ∴BE//CD ∴△ABE∽△ACD ∴,即,解得CD=17.5m. 故答案为A. 【点睛】本题考查了相似三角形的应用,正确判定相似三角形并利用相似三角形的性质列方程计算是解答本题的关键. 12.(2020•福建省•4分)如图,面积为1的等边三角形ABC中,D,E,F分别是AB,BC,CA的中点,则△DEF的面积是( ) A.1 B. C. D. 【分析】根据三角形的中位线定理和相似三角形的判定和性质定理即可得到结论. 【解答】解:∵D,E,F分别是AB,BC,CA的中点, ∴DE=AC,DF=BC,EF=AB, ∴=, ∴△DEF∽△ABC, ∴=()2=()2=, ∵等边三角形ABC的面积为1, ∴△DEF的面积是, 故选:D. 【点评】本题考查了三角形中位线定理,等边三角形的性质,相似三角形的判定和性质,熟练掌握三角形的中位线定理是解题的关键. 13. (2020•四川省泸州市•3分)古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段MN分为两线段MG,GN,使得其中较长的一段MG是全长MN与较短的一段GN的比例中项,即满足==,后人把这个数称为“黄金分割”数,把点G称为线段MN的“黄金分割”点.如图,在△ABC中,已知AB=AC=3,BC=4,若D,E是边BC的两个“黄金分割”点,则△ADE的面积为( ) A.10﹣4 B.3﹣5 C. D.20﹣8 【分析】作AH⊥BC于H,如图,根据等腰三角形的性质得到BH=CH=BC=2,则根据勾股定理可计算出AH=,接着根据线段的“黄金分割”点的定义得到BE=BC=2﹣2,则计算出HE=2﹣4,然后根据三角形面积公式计算. 【解答】解:作AH⊥BC于H,如图, ∵AB=AC, ∴BH=CH=BC=2, 在Rt△ABH中,AH==, ∵D,E是边BC的两个“黄金分割”点, ∴BE=BC=2(﹣1)=2﹣2, ∴HE=BE﹣BH=2﹣2﹣2=2﹣4, ∴DE=2HE=4﹣8 ∴S△ADE=×(4﹣8)×=10﹣4. 故选:A. 【点评】本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点.其中AC=AB≈0.618AB,并且线段AB的黄金分割点有两个.也考查了等腰三角形的性质. 14. (2020•四川省内江市•3分)如图,在△ABC中,D.E分别是AB和AC的中点,S四边形BCED=15,则S△ABC=( ) A.30 B.25 C.22.5 D.20 【分析】先根据三角形中位线的性质,证得:DE∥BC,DE=BC,进而得出△ADE∽△ABC,又由相似三角形面积的比等于相似比的平方即可求得答案. 【解答】解:∵D.E分别是AB.AC边上的中点, ∴DE∥BC,DE=BC, ∴△ADE∽△ABC, ∴=()2=, ∴S△ADE:S四边形BCED=1:3, 即S△ADE:15=1:3, ∴S△ADE=5, ∴S△ABC=5+15=20. 故选:D. 【点评】此题考查了三角形中位线定理以及相似三角形的判定与性质.注意相似三角形的面积的比等于相似比的平方. 二. 填空题 1. (2020•山东省威海市•3分)如图,点C在∠AOB的内部,∠OCA=∠OCB,∠OCA与∠AOB互补.若AC=1.5,BC=2,则OC= . 【分析】通过证明△ACO∽△OCB,可得,可求OC=. 【解答】解:∵∠OCA=∠OCB,∠OCA与∠AOB互补, ∴∠OCA+∠AOB=180°,∠OCB+∠AOB=180°, ∵∠OCA+∠COA+∠OAC=180°,∠OCB+∠OBC+∠COB=180°, ∴∠AOB=∠COA+∠OAC,∠AOB=∠OBC+∠COB, ∴∠AOC=∠OBC,∠COB=∠OAC,∴△ACO∽△OCB,∴, ∴OC2=2×=3,∴OC=,故答案为. 【点评】本题考查了相似三角形的判定和性质,证明△ACO∽△OCB是本题的关键. 2.(2020•广东省深圳市•3分)如图,已知四边形ABCD,AC与BD相交于点O,∠ABC=∠DAC=90°,,,则= . 【考点】三角形形似 【答案】 【解析】过B点作BE//AD交AC于点E,则BE⊥AD,△ADO∽△EBO, ∴,由可得CE=2BE=4AE, ∴ 3.(2020•广东省广州市•3分)如图,正方形中,绕点逆时针旋转到 ,,分别交对角线于点,若,则的值为_______. 【答案】16 【解析】 【分析】 根据正方形及旋转的性质可以证明,利用相似的性质即可得出答案. 【详解】解:在正方形中,, ∵绕点逆时针旋转到, ∴, ∴, ∵, ∴, ∴, ∴. 故答案为:16. 【点睛】本题考查了正方形的性质,旋转的性质,相似三角形的判定及性质,掌握正方形的性质,旋转的性质,相似三角形的判定及性质是解题的关键. 4. (2020•山东东营市•4分)如图,为平行四边形边上一点,分别为上的点,且的面积分别记为.若则____. 【答案】 【解析】 【分析】 证明△PEF∽△PAD,再结合△PEF的面积为2可求出△PAD的面积,进而求出平行四边形ABCD的面积,再用平行四边形ABCD的面积减去△PAD的面积即可求解. 【详解】解:∵ ∴,且∠APD=∠EPF, ∴△PEF∽△PAD, 根据相似三角形面积比等于相似比的平方,且△PEF的面积为2可知, , ∴, 过P点作平行四边形ABCD的底AD上的高PH, ∴, ∴ , 即平行四边形ABCD的面积为, ∴. 故答案为:. 【点睛】本题考查了平行四边形性质,相似三角形的判定及性质等,熟练掌握其性质是解决本题的关键. 5. (2020•四川省攀枝花市•8分)三角形三条边上的中线交于一点,这个点叫三角形的重心.如图G是△ABC的重心.求证:AD=3GD. 【分析】根据题意,可以得到DE时△ABC的中位线,从而可以得到DE∥AC且DE=AC,然后即可得到△DEG∽△ACG,即可得到DG和AG的比值,从而可以得到DG和AD的比值,然后即可得到AD和GD的关系. 【解答】证明:连接DE, ∵点G是△ABC的重心, ∴点E和点D分别是AB和BC的中点, ∴DE是△ABC的中位线, ∴DE∥AC且DE=AC, ∴△DEG∽△ACG, ∴, ∴, ∴, ∴AD=3DG, 即AD=3GD. 【点评】本题考查三角形的重心、三角形的中位线、三角形相似,解答本题的关键是明确题意,利用数形结合的思想解答. 三.解答题 1.(2020•广东省深圳市•8分)如图,AB为⊙O的直径,点C在⊙O上,AD与过点C的切线互相垂直,垂足为D.连接BC并延长,交AD的延长线于点E (1)求证:AE=AB (2)若AB=10,BC=6,求CD的长 【考点】圆的证明与计算 【解析】 解:(1)证:连接OC ∵CD与相切于C点 ∴OC⊥CD 又∵CD⊥AE ∴OC//AE ∴ ∵OC=OB ∴ ∴ ∴AE=AB (2)连接AC ∵AB为的直径 ∴ ∴ ∵AB=AE,AC⊥BE ∴EC=BC=6 ∵, ∴△EDC∽△ECA ∴ ∴ 2.(2020•广东省深圳市•9分)背景:一次小组合作探究课上,小明将两个正方形按背景图位置摆放(点E,A,D在同一条直线上), 发现BE=DG且BE⊥DG。 小组讨论后,提出了三个问题,请你帮助解答: (1)将正方形AEFG绕点A按逆时针方向旋转,(如图1)还能得到BE=DG吗?如果能,请给出证明.如 若不能,请说明理由: (2)把背景中的正方形分别改为菱形AEFG和菱形ABCD,将菱形AEFG绕点A按顺时针方向旋转,(如图2)试问当∠EAG与∠BAD的大小满足怎样的关系时,背景中的结论BE=DG仍成立?请说明理由; (3)把背景中的正方形改成矩形AEFG和矩形ABCD,且,AE=4,AB=8,将矩形AEFG绕点A按顺时针方向旋转(如图3),连接DE,BG。小组发现:在旋转过程中, BG2+DE2是定值,请求出这个定值 背景图 图3 图2 图1 【考点】手拉手,相似,勾股 【解析】 解:(1)证明:∵四边形ABCD为正方形 ∴AB=AD, ∵四边形AEFG为正方形 ∴AE=AG, ∴ 在△EAB和△GAD中有: ∴△EAB≌△GAD ∴BE=DG (2)当∠EAG=∠BAD时,BE=DG成立。 证明:∵四边形ABCD菱形 ∴AB=AD ∵四边形AEFG为正方形 ∴AE=AG ∵∠EAG=∠BAD ∴ ∴ 在△EAB和△GAD中有: ∴△EAB≌△GAD ∴BE=DG (3)连接EB,BD,设BE和GD相交于点H ∵四边形AEFG和ABCD为矩形 ∴ ∴ ∵ ∴△EAB∽△GAD ∴ ∴ ∴, ∴ , ∴ 3.(2020•广东省•8分)如题22图,在四边形ABCD中,AD∥BC,∠DAB=90°,AB是⊙O的直径,CO平分∠BCD. (1)求证:直线CD与⊙O相切; (2)如题22﹣2图,记(1)中的切点为E,P为优弧上一点,AD=1,BC=2,求tan∠APE的值. E 【答案】 (1) 证明:过点O作OE⊥CD交于点E ∵AD∥BC,∠DAB=90° ∴∠OBC=90°即OB⊥BC ∵OE⊥CD,OB⊥BC,CO平分∠BCD ∴OB=OE ∵AB是⊙O的直径 ∴OE是⊙O的半径 ∴直线CD与⊙O相切 (2)连接OD.OE ∵由(1)得,直线CD.AD.BC与⊙O相切 ∴由切线长定理可得AD=DE=1,BC=CE=3, ∠ADO=∠EDO,∠BCO=∠ECO ∴∠AOD=∠EOD,CD=3 ∵= ∴∠APE=∠AOE=∠AOD ∵AD∥BC ∴∠ADE+∠BCE=180° ∴∠EDO+∠ECO=90°即∠DOC=90° ∵OE⊥DC,∠ODE=∠CDO ∴△ODE∽△CDO ∴即 ∴OD= ∵在Rt△AOD中,AO= ∴tan∠AOD== ∴tan∠APE= 【解析】无切点作垂直证半径,切线长定理,直角三角形的判定,相似三角形的运用、辅助线的作法 【考点】切线的判定、切线长定理、圆周角定理、相似三角形、三角函数 4.(2020•广东省•10分)如题25图,抛物线y=与x轴交于点A.B,点A.B分别位于原点的左、右两侧,BO=3AO=3,过点B的直线与y轴正半轴和抛物线的交点分别为C.D,BC=CD. (1)求B.c的值; (2)求直线BD的直线解析式; (3)点P在抛物线的对称轴上且在x轴下方,点Q在射线BA上.当△ABD与△BPQ相似时,请直接写出所有满足条件的点Q的坐标. 【答案】 解:(1)由题意得A(-1,0),B(3,0),代入抛物线解析式得 ,解得 (2)过点D作DE⊥x轴交于点E ∵OC∥OC,BC=CD,OB=3 ∴ ∴OE= ∴点D的横坐标为xD=- ∵点D是射线BC与抛物线的交点 ∴把xD=-代入抛物线解析式得yD=+1 ∴D(-,+1) 设直线BD解析式为y=kx+m,将B(3,0)、D(-,+1)代入 ,解得 ∴直线BD的直线解析式为y= (3)由题意得tan∠ABD=,tan∠ADB=1 由题意得抛物线的对称轴为直线x=1,设对称轴与x轴交点为M,P(1,n)且n<0,Q(x,0)且x<3 ①当△PBQ∽△ABD时,tan∠PBQ=tan∠ABD即=,解得-n= tan∠PQB=tan∠ADB,即=1,解得x= ②当△PQB∽△ABD时,tan∠PBQ=tan∠ADB即=1,解得-n=2 tan∠QPB=tan∠ABD,即=,解得x= ③当△PQB∽△DAB时,tan∠PBQ=tan∠ABD即=,解得-n= tan∠PQM=tan∠DAE,即=,解得x= ④当△PQB∽△ABD时,tan∠PBQ=tan∠ABD即=1,解得-n=2 tan∠PQM=tan∠DAE,即=,解得x= 综上所述,Q1(,0)、Q2(,0)、Q3(,0)、Q4(,0) 【解析】分类讨论不重不漏,计算能力要求高 【考点】一次函数、二次函数、平面直角坐标系、相似三角形、三角函数、分类讨论、二次根式计算 5.(2020•贵州省安顺市•10分)如图,AB为⊙O的直径,四边形ABCD内接于⊙O,对角线 AC,BD交于点E,⊙O的切线AF交BD的延长线于点F,切点为A,且∠CAD=∠ABD. (1)求证:AD=CD; (2)若AB=4,BF=5,求sin∠BDC的值. 【分析】(1)根据圆周角定理得∠ABD=∠ACD,进而得∠ACD=∠CAD,便可由等腰三角形判定定理得AD=CD; (2)证明△ADF≌△ADE,得AE=AF,DE=DF,由勾股定理求得AF,由三角形面积公式求得AD,进而求得DE,BE,再证明△BEC∽△AED,得BC,进而求得sin∠BAC便可. 【解答】解:(1)证明:∵∠CAD=∠ABD, 又∵∠ABD=∠ACD, ∴∠ACD=∠CAD, ∴AD=CD; (2)∵AF是⊙O的切线, ∴∠FAB=90°, ∵AB是⊙O的直径, ∴∠ACB=∠ADB=∠ADF=90°, ∴∠ABD+∠BAD=∠BAD+∠FAD=90°, ∴∠ABD=∠FAD, ∵∠ABD=∠CAD, ∴∠FAD=∠EAD, ∵AD=AD, ∴△ADF≌△ADE(ASA), ∴AF=AE,DF=DE, ∵AB=4,BF=5, ∴AF=, ∴AE=AF=3, ∵, ∴, ∴DE=, ∴BE=BF﹣2DE=, ∵∠AED=∠BEC,∠ADE=∠BCE=90°, ∴△BEC∽△AED, ∴, ∴, ∴, ∵∠BDC=∠BAC, ∴. 【点评】本题主要考查了圆的切线的性质,圆周角定理,相似三角形的性质与判定,全等三角形的性质与判定,等腰三角形的性质与判定,解直角三角形的应用,勾股定理,关键是证明三角形全等与相似. 6.(2020•广东省广州市•7分)如图,平面直角坐标系中,的边在 轴上,对角线,交于点,函数的图象经过点和点. (1)求的值和点的坐标; (2)求的周长. 【答案】(1)k=12,M(6,2);(2)28 【解析】 【分析】 (1)将点A(3,4)代入中求出k值,作AD⊥x轴于点D,ME⊥x轴于点E,证明△MEC∽△ADC,得到,求出ME=2,代入即可求出点M的坐标; (2)根据勾股定理求出OA=5,根据点A.M的坐标求出DE,即可得到OC的长度,由此求出答案. 【详解】(1)将点A(3,4)代入中,得k=, ∵四边形OABC是平行四边形, ∴MA=MC, 作AD⊥x轴于点D,ME⊥x轴于点E, ∴ME∥AD, ∴△MEC∽△ADC, ∴, ∴ME=2, 将y=2代入中,得x=6, ∴点M的坐标为(6,2); (2)∵A(3,4), ∴OD=3,AD=4, ∴, ∵A(3,4),M(6,2), ∴DE=6-3=3, ∴CD=2DE=6, ∴OC=3+6=9, ∴的周长=2(OA+OC)=28. 【点睛】此题考查平行四边形的性质,待定系数法求反比例函数的解析式,求函数图象上点的坐标,勾股定理,相似三角形的判定及性质. 7.(2020•贵州省安顺市•10分)如图,四边形ABCD是矩形,E是BC边上一点,点F在BC的延长线上,且CF=BE. (1)求证:四边形AEFD是平行四边形; (2)连接ED,若∠AED=90°,AB=4,BE=2,求四边形AEFD的面积. 【分析】(1)先根据矩形的性质得到AD∥BC,AD=BC,然后证明AD=EF可判断四边形AEFD是平行四边形; (2)连接DE,如图,先利用勾股定理计算出AE=2,再证明△ABE∽△DEA ,利用相似比求出AD,然后根据平行四边形的面积公式计算. 【解答】(1)证明:∵∠四边形ABCD是矩形, ∴AD∥BC,AD=BC, ∵BE=CF, ∴BE+EC=EC+EF,即BC=EF, ∴AD=EF, ∴四边形AEFD是平行四边形; (2)解:连接DE,如图, ∵四边形ABCD是矩形, ∴∠B=90°, 在Rt△ABE中,AE==2, ∵AD∥BC, ∴∠AEB=∠EAD, ∵∠B=∠AED=90°, ∴△ABE∽△DEA, ∴AE:AD=BE:AE, ∴AD==10, ∴四边形AEFD的面积=AB×AD=2×10=20. 【点评】本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形,灵活运用相似三角形的性质表示线段之间的关系;也考查了平行四边形的判定和矩形的性质. 8.(2020•山东菏泽市•10分)如图1,四边形ABCD的对角线AC,BD相交于点O,OA= OC,OB=OD+CD. (1)过点A作AE∥DC交BD于点E,求证:AE=BE; (2)如图2,将△ABD沿AB翻折得到△ABD'. ①求证:BD'∥CD; ②若AD'∥BC,求证:CD2=2OD•BD. 【分析】(1)证明△AOE≌△COD(AAS),由全等三角形的性质得出CD=AE,OD=OE,则可得出结论; (2)①过点A作AE∥DC交BD于点E,由(1)得出∠ABE=∠AEB,由折叠的性质可得出∠ABD'=∠BAE,则BD'∥AE,可得出结论; ②过点A作AE∥DC交BD于点E,延长AE交BC于点F,证明△AED∽△BEF,得出,证明△BEF∽△BDC,由相似三角形的性质得出=,根据AE=CD,DE=2OD可得出结论. 【解答】(1)证明:∵AE∥DC, ∴∠CDO=∠AEO,∠EAO=∠DCO, 又∵OA=OC, ∴△AOE≌△COD(AAS), ∴CD=AE,OD=OE, ∵OB=OE+BE,OB=OD+CD, ∴BE=CD, ∴AE=BE; (2)①证明:如图1,过点A作AE∥DC交BD于点E, 由(1)可知△AOE≌△COD,AE=BE, ∴∠ABE=∠AEB, ∵将△ABD沿AB翻折得到△ABD', ∴∠ABD'=∠ABD, ∴∠ABD'=∠BAE, ∴BD'∥AE, 又∵AE∥CD ∴BD'∥CD. ②证明:如图2,过点A作AE∥DC交BD于点E,延长AE交BC于点F, ∵AD'∥BC,BD'∥AE, ∴四边形AD'BF为平行四边形. ∴∠D'=∠AFB, ∵将△ABD沿AB翻折得到△ABD'. ∴∠D'=∠ADB, ∴∠AFB=∠ADB, 又∵∠AED=∠BEF, ∴△AED∽△BEF, ∴, ∵AE=CD, ∴, ∵EF∥CD, ∴△BEF∽△BDC, ∴=, ∴, ∴CD2=DE•BD, ∵△AOE≌△COD, ∴OD=OE, ∴DE=2OD, ∴CD2=2OD•BD. 【点评】本题是相似形综合题,考查了翻折的性质,全等三角形的判定与性质,相似三角形的判定与性质,平行线的判定与性质,等腰三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题的关键. . 9. (2020•福建省•12分)如图,△ADE由△ABC绕点A按逆时针方向旋转90°得到,且点B的对应点D恰好落在BC的延长线上,AD,EC相交于点P. (1)求∠BDE的度数; (2)F是EC延长线上的点,且∠CDF=∠DAC. ①判断DF和PF的数量关系,并证明; ②求证:=. 【分析】(1)由旋转的性质得出AB=AD,∠BAD=90°,△ABC≌△ADE,得出∠ADE=∠ B=45°,可求出∠BDE的度数; (2)①由旋转的性质得出AC=AE,∠CAE=90°,证得∠FPD=∠FDP,由等腰三角形的判定得出结论; ②过点P作PH∥ED交DF于点H,得出∠HPF=∠DEP,,证明△HPF≌△CDF(ASA),由全等三角形的性质得出HF=CF,则可得出结论. 【解答】解:(1)∵△ADE由△ABC绕点A按逆时针方向旋转90°得到, ∴AB=AD,∠BAD=90°,△ABC≌△ADE, 在Rt△ABD中,∠B=∠ADB=45°, ∴∠ADE=∠B=45°, ∴∠BDE=∠ADB+∠ADE=90°. (2)①DF=PF. 证明:由旋转的性质可知,AC=AE,∠CAE=90°, 在Rt△ACE中,∠ACE=∠AEC=45°, ∵∠CDF=∠CAD,∠ACE=∠ADB=45°, ∴∠ADB+∠CDF=∠ACE+∠CAD, 即∠FPD=∠FDP, ∴DF=PF. ②证明:过点P作PH∥ED交DF于点H, ∴∠HPF=∠DEP,, ∵∠DPF=∠ADE+∠DEP=45°+∠DEP, ∠DPF=∠ACE+∠DAC=45°+∠DAC, ∴∠DEP=∠DAC, 又∵∠CDF=∠DAC, ∴∠DEP=∠CDF, ∴∠HPF=∠CDF, 又∵FD=FP,∠F=∠F, ∴△HPF≌△CDF(ASA), ∴HF=CF, ∴DH=PC, 又∵, ∴. 【点评】本题是相似形综合题,考查了旋转的性质,三角形内角与外角的关系,等腰三角形的判定,全等三角形的判定与性质,平行线的性质,平行线分线段成比例定理等知识,熟练掌握相似三角形的判定与性质是解题的关键. 10. (2020•四川省凉山州•7分)如图,一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB.AC上,这个正方形零件的边长是多少? 【分析】根据正方形的对边平行得到BC∥EF,利用“平行于三角形的一边的直线截其它两边或其它两边的延长线,得到的三角形与原三角形相似”,设正方形零件的边长为xmm,则KD=EF=x,AK=80﹣x,根据相似三角形的性质得到比例式,解方程即可得到结果. 【解答】解:∵四边形EGFH为正方形, ∴BC∥EF, ∴△AEF∽△ABC; 设正方形零件的边长为x mm,则KD=EF=x,AK=80﹣x, ∵EF∥BC, ∴△AEF∽△ABC, ∵AD⊥BC, ∴=, ∴=, 解得:x=48. 答:正方形零件的边长为48mm. 【点评】本题考查了正方形的性质、相似三角形的应用,注意数形结合的运用是解题关键. 11. (2020•四川省乐山市•9分)如图,是矩形的边上的一点,于点,,,.求的长度. 【答案】. 【解析】 【分析】 先根据矩形的性质、勾股定理求出,再根据相似三角形的判定与性质可得,由此即可得出答案. 【详解】∵四边形是矩形, ∴, ∵ ∴ ∵, , ∴ 在和中, ∴ ∴,即 解得 即的长度为. 【点睛】本题考查了矩形性质、勾股定理、相似三角形的判定与性质等知识点,掌握相似三角形的判定与性质是解题关键. 12. (2020•山东省枣庄市•10分)在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC.BC的延长线相交,交点分别为点E.F,DF与AC交于点M,DE与BC交于点N. (1)如图1,若CE=CF,求证:DE=DF; (2)如图2,在∠EDF绕点D旋转的过程中,试证明CD2=CE•CF恒成立; (3)若CD=2,CF=,求DN的长. 【分析】(1)根据等腰直角三角形的性质得到∠ACD=∠BCD=45°,证明△DCF≌△DCE,根据全等三角形的对应边相等证明结论; (2)证明△FCD∽△DCE,根据相似三角形的性质列出比例式,整理即可证明结论; (3)作DG⊥BC,根据等腰直角三角形的性质求出DG,由(2)的结论求出CE,证明△ENC∽△DNG,根据相似三角形的性质求出NG,根据勾股定理计算,得到答案. 【解答】(1)证明:∵∠ACB=90°,AC=BC,CD是中线, ∴∠ACD=∠BCD=45°,∠ACF=∠BCE=90°,∴∠DCF=∠DCE=135°, 在△DCF和△DCE中, , ∴△DCF≌△DCE(SAS),∴DE=DF; (2)证明:∵∠DCF=135°,∴∠F+∠CDF=45°,∵∠FDE=45°,∴∠CDE+∠CDF=45°,∴∠F=∠CDE, ∵∠DCF=∠DCE,∠F=∠CDE,∴△FCD∽△DCE,∴=,∴CD2=CE•CF; (3)解:过点D作DG⊥BC于G,∵∠DCB=45°,∴GC=GD=CD=, 由(2)可知,CD2=CE•CF,∴CE==2, ∵∠ECN=∠DGN,∠ENC=∠DNG,∴△ENC∽△DNG, ∴=,即=,解得,NG=, 由勾股定理得,DN==. 【点评】本题考查的是相似三角形的判定和性质、全等三角形的判定和性质、等腰直角三角形的性质,掌握相似三角形的判定定理和性质定理是解题的关键. 13.(2020•辽宁省营口市•12分)如图,在矩形ABCD中,AD=kAB(k>0),点E是线段CB延长线上的一个动点,连接AE,过点A作AF⊥AE交射线DC于点F. (1)如图1,若k=1,则AF与AE之间的数量关系是 AF=AE ; (2)如图2,若k≠1,试判断AF与AE之间的数量关系,写出结论并证明;(用含k的式子表示) (3)若AD=2AB=4,连接BD交AF于点G,连接EG,当CF=1时,求EG的长. 【考点】SO:相似形综合题. 【专题】152:几何综合题;556:矩形 菱形 正方形;55D:图形的相似;66:运算能力;67:推理能力. 【分析】(1)证明△EAB≌△FAD(AAS),由全等三角形的性质得出AF=AE; (2)证明△ABE∽△ADF,由相似三角形的性质得出,则可得出结论; (3)①如图1,当点F在DA上时,证得△GDF∽△GBA,得出,求出AG= .由△ABE∽△ADF可得出=,求出AE=.则可得出答案; ②如图2,当点F在DC的延长线上时,同理可求出EG的长. 【解答】解:(1)AE=AF. ∵AD=AB,四边形ABCD矩形, ∴四边形ABCD是正方形, ∴∠BAD=90°, ∵AF⊥AE, ∴∠EAF=90°, ∴∠EAB=∠FAD, ∴△EAB≌△FAD(AAS), ∴AF=AE; 故答案为:AF=AE. (2)AF=kAE. 证明:∵四边形ABCD是矩形, ∴∠BAD=∠ABC=∠ADF=90°, ∴∠FAD+∠FAB=90°, ∵AF⊥AE, ∴∠EAF=90°, ∴∠EAB+∠FAB=90°, ∴∠EAB=∠FAD, ∵∠ABE+∠ABC=180°, ∴∠ABE=180°﹣∠ABC=180°﹣90°=90°, ∴∠ABE=∠ADF. ∴△ABE∽△ADF, ∴, ∵AD=kAB, ∴, ∴, ∴AF=kAE. (3)解:①如图1,当点F在DA上时, ∵四边形ABCD是矩形, ∴AB=CD,AB∥CD, ∵AD=2AB=4, ∴AB=2, ∴CD=2, ∵CF=1, ∴DF=CD﹣CF=2﹣1=1. 在Rt△ADF中,∠ADF=90°, ∴AF===, ∵DF∥AB, ∴∠GDF=∠GBA,∠GFD=∠GAB, ∴△GDF∽△GBA, ∴, ∵AF=GF+AG, ∴AG=. ∵△ABE∽△ADF, ∴=, ∴AE==. 在Rt△EAG中,∠EAG=90°, ∴EG===, ②如图2,当点F在DC的延长线上时,DF=CD+CF=2+1=3, 在Rt△ADF中,∠ADF=90°, ∴AF===5. ∵DF∥AB, ∵∠GAB=∠GFD,∠GBA=∠GDF, ∴△AGB∽△FGD, ∴=, ∵GF+AG=AF=5, ∴AG=2, ∵△ABE∽△ADF, ∴, ∴AE=, 在Rt△EAG中,∠EAG=90°, ∴EG===. 综上所述,EG的长为或.查看更多