数学冀教版七年级上册课件2-7 角的和与差

数学冀教版七年级上册课件2-7 角的和与差

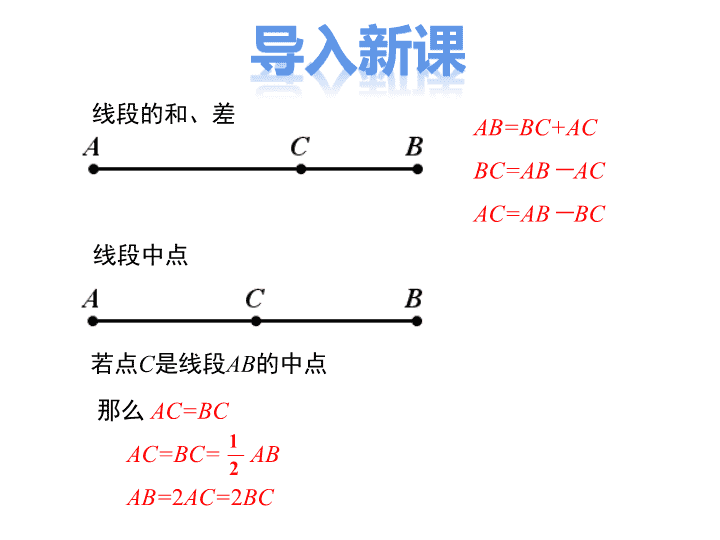
2.7 角的和与差 导入新课 讲授新课 当堂练习 课堂小结 1.理解角的和差、角平分线的几何意义；(重点） 2.掌握角之间的和差关系，并能进行简单的计算；（难点） 3.了解余角与补角的概念，理解余角与补角的性质并会进 行运用.（重点、难点） AB=BC+AC BC=AB－AC AC=AB－BC 线段的和、差 线段中点 那么 AC=BC AC=BC= AB AB=2AC=2BC 1 2 若点C是线段AB的中点 角的和、差关系 图中有几个角？它们之间有什么关系？ 图中有3个角. ∠AOB+∠BOC=∠AOC；它们的关系有: ∠AOC－∠BOC=∠AOB； ∠AOC－∠AOB=∠BOC. O C B 例1 如图：O是直线AB上一点，∠AOC＝53°. 求∠BOC的度数. 解：因为∠AOB是平角 ∠AOB＝∠AOC+∠BOC 所以∠BOC＝∠AOB－∠AOC ＝180°－53° ＝127°. A 例2 已知∠1＝103 °24 ′28″， ∠2 ＝30 °54 ″，求 ∠1＋ ∠2和∠1－ ∠2 . 解：∠1＋ ∠2＝ 103°24′28″＋ 30°54 ″ 　　　　　　＝133°24′82 ″ 　　　　　　＝133°25′22 ″ 103°24′28″ ＋30° 54 ″ 133°24′82 ″ (82 ″=1′22 ″) 所以 ∠1＋ ∠2= 133°25′22 ″ A B O 12 C 　　∠1一 ∠2＝ 103°24′28″－ 30°54 ″ 　　　　　　＝103°23′88 ″－ 30°54 ″ 　　　　　　＝73°23′34 ″ 103°24′28″ — 30° 54 ″ 73°23′34″ (24′28 ″=23′88 ″) 所以 ∠1— ∠2= 73°23′24 ″. 例3.计算： （1）37°28′+ 24°35′； （2）83°20′-45°38′20″； （3）25°53′28″×5； （4）15°20′÷6. 解：（1） 37°28′+ 24°35′ = 61°63′ = 62°3′； （2） 83°20′- 45°38′20″ = 82°79′60″- 45°38′20″ = 37°41′40″. 解：（3）25°53′28″×5 ＝25°×5＋53′×5＋28″×5 ＝125°＋265′＋140″＝129°27′20″. （4）15°20′÷6 ＝12°200′÷6＝12°÷6＋200′÷6 ＝2°＋198′÷6＋2′÷6 ＝2°＋33′＋120″÷6 ＝2°33′20″. 在进行度、分、秒的加、减、乘、除运算时，要注 意三点： ①度、分、秒均是60进制的； ②加、减法的运算，可以本着“度与度加减、分与 分加减、秒与秒加减，不够减的时候借位”的原则； ③乘、除法运算可以按分配律来进行，不够除可以 把余数化为低位的再除． [归纳总结] 角平分线 在一张透明纸上任意画一个角∠ AOB (如右图),把这 张透明纸折叠,使角的两边OA和OB重合,然后把这张纸 展开、铺平，画出折痕OC. ∠ AOC与∠ BOC之间有怎 样的大小关系？ ∠ AOC=∠ BOC O A B C 从一个角的顶点引出的一条射线，把这个角 分成的两个角相等，这条射线叫做这个角的 平分线. O A B C 如上图射线OC是∠AOB的角平分线或OC平分∠AOB，记做： ∠AOC=∠BOC= ∠AOB 或 ∠AOB=2∠AOC=2∠BOC 1 2 几何写法： 提醒：角的平分线是射线 例4 如图，OB是∠ AOC的平分线，OD是∠COE的平分 线. (1)如果∠ AOC=80°，那么∠BOC是多少度？ O E D C B A 解：因为OB平分∠ AOC， ∠ AOC=80° 所以∠BOC=∠AOB=40°. 所以∠AOB= ∠AOC=80× =40°. 1 2 1 2 (2)如果∠ AOB=40°， ∠ DOE=30°， 那么∠BOD是多少度？ O E D C B A 解：因为OB平分∠ AOC， 所以∠BOC=∠AOB=40°. 因为OD平分∠ COE， 所以∠COD=∠DOE=30°. 所以 ∠BOD=∠BOC+∠COD=40°+30°=70°. (3)如果∠ AOE=140°， ∠ COD=30°， 那么∠AOB是多少度？ O E D C B A 解：因为∠ COD=30°， 所以∠COE=2∠COD=60°， 所以∠AOC=∠AOE－∠COE=140°－ 60°=80°， 因为OB平分∠ AOC， 所以∠AOB= ∠AOC= ×80°=40°. 1 2 1 2 1.如图：OC是∠AOB的平分线，OD是∠BOC的平 分线，那么下列各式中正确的是：( ) 2.如图，OC是平角∠AOB的角平分线， ∠COD=32°，求∠AOD的度数. 1 2A B 2 3 1 3C D 3 2 COD AOC AOD AOB BOD AOB BOC AOB             ． ． ． ． D C O BA A ∠AOD=122°. 角的互补与互余 2 1 如果两个角的和等于90°，那么说这两个角互为余角 (简称互余)，也说其中一个角是另一个角的余角. 定义： 如图，可以说∠1是∠2的余角或∠2是∠1的余角. 图中给出的各角，那些互为余角？ 15o 24o 66o 75o 46.2o 43.8o 3 4 如果两个角的和等于一个180°，那么说这两个角互为 补角(简称互补)，也说其中一个角是另一个角的补角. 定义： 如图，可以说∠3是∠4的余角或∠4是∠3的补角. 例5 如图，∠CDF＝90°，AD是一条射线，则∠1 的余角和补角各是哪个角？ 解：因为∠CDF＝90°，即∠1＋ ∠ADC＝90°，所以∠1的余角是 ∠ADC. 因为∠EDF是一个平角，所以 ∠1＋∠ADE＝180°，所以∠1 的补角是∠ADE. 图中给出的各角，那些互为补角？ 10o 30o 60o 80o 100o 120o 150o 170o ∠1与∠2，∠3都互为补角， ∠2与∠3的大小有什么关系？ 思考： 1 2 同角(等角)的补角相等 结论： 3 ∠2=180°－∠1 ∠3=180°－∠1 同角(等角)的余角相等 类似的可以得到： 例6 如图所示，已知∠AOC＝∠BOD＝90°，且∠AOB＝40°， 求∠COD的度数． 解：因为∠AOC＝∠BOD＝90°， 所以∠AOB＋∠BOC＝∠COD＋∠BOC＝90°， 所以∠AOB，∠COD都是∠BOC的余角， 所以∠AOB＝∠COD. 因为∠AOB＝40°，所以∠COD＝40°. 例7 一个角的补角比它的余角的2倍多12°，求这个 角的度数. 解：设这个角的度数为x°. 所以它的补角为（180-x)°， 它的余角为（90-x）°， 依题意，得 180-x=2(90-x)+12. 解方程，得 x=12. 答：这个角的度数为12°. 2.下列四个角中，最有可能与70°角互余的角是(　　) 1.如图，点O在直线AB上，若∠1＝40°，则∠2的 度数是(　　) A．50° B．60° C．140° D．150° C A 3．如图，直线AB，CD相交于点O，射线OM 平分∠AOC，∠MON＝90°.若∠AOM＝35°， 则∠CON的度数为(　　) A．35° B．45° C．55° D．65° C 4.如图：OC是∠AOB的平分线，OD是∠BOC的 平分线，那么下列各式中正确的是：( ) 1 2A B 2 3 1 3C D 3 2 COD AOC AOD AOB BOD AOB BOC AOB             ． ． ． ． A 5. 如图，∠AOB与∠BOD互为余角，OC是 ∠BOD的平分线，∠AOB=29.66°，求∠COD的度数. 解：因为∠AOB与∠BOD互为余角， 所以∠BOD = 90°-∠AOB = 90°-29.66°= 60.34°. 又因为OC是∠BOD的平分线， 因此，∠COD 的度数为 30.17°. 29.66° 60.34° 所以 1 1= = 60.34 =30.17 .2 2∠ ∠ ×COD BOD ° ° 30.17° 6.已知一个角的余角是这个角的补角的 ， 求这个角的度数 1 3 解：设这个角为x°， 则这个角的余角为（90-x）°， 补角为（180-x）°. 根据题意，得 ， 解得 x = 45 . 因此，这个角的度数为45°. 190 = 1803x x( )- - 角的和与差 角的和与差 {角的平分线 角的互补与互余