- 2021-04-21 发布 |
- 37.5 KB |
- 15页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学冀教版九年级上册课件25-2平行线分线段成比例
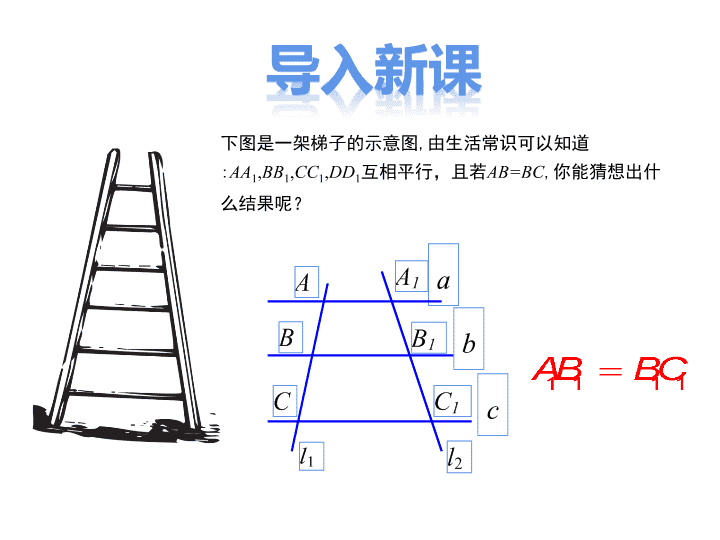
25.2平行线分线段成比例 导入新课 讲授新课 当堂练习 课堂小结 情境引入 1.学习并掌握平行线分线段成比例定理并学会运用. 2.了解并掌握平行线分线段成比例定理的推论. (重点) 3.能够运用平行线分线段成比例定理及推论解决问题.(难点) 下图是一架梯子的示意图,由生活常识可以知道 :AA1,BB1,CC1,DD1互相平行,且若AB=BC,你能猜想出 什么结果呢? a b c 平行线分线段成比例定理(基本事实) 如图(1)小方格的边长都是1,直线a ∥b∥c ,分别交直线 m,n于 (1)计算 你有什么发现?1 2 1 2 2 3 2 3 ,A A B B A A B B .,,,, 321,321 BBBAAA (2) 将b向下平移到如下图2的位置,直线m,n与直 线b的交点分别为 .你在问题(1)中发现的结论还 成立吗?如果将b平移到其他位置呢? (图2) 22 , BA (3)在平面上任意作三条平行线,用它们截两条直线, 截得的线段成比例吗? 归纳 基本事实:两条直线被一组平行线所截,所截得的 对应线段成比例; 符号语言: 若a ∥b∥ c ,则 . 1 2 1 2 2 3 2 3 A A B B A A B B 1.如何理解“对应线段”? 2.“对应线段”成比例都有哪些表达形式? 议一议 平行线分线段成比例的推论 如图3,直线a ∥b∥ c ,分别交直线m,n于 A1,A2,A3,B1, B2,B3 .过点A1作直线n的平行线,分别交直线b,c于点C2, C3.如图4 ,图4中有哪些成比例线段? (图3) (图4) aa bb cc nmnm A1 B2A2 B1A1B1 C1 C2 A2 B2 A3 B3 A3 B3 推论1: 平行于三角形一边的直线截其他两边(或两边的延长 线),所得的对应线段成比例. 推论2: 平行于三角形的一边,并且和其他两边相交的直线, 所截得的三角形与原三角形的对应边成比例 归纳 1.如图所示,在△ABC中,E,F,分别是AB和AC的点,且 EF∥BC. (1)如果AE=7,EB=5,FC=4,那么AF的长是多少? A E B C F 解: ∵EF∥BC, ∴ ∵AE = 7, EB = 5 , FC = 4. ∴ .AE AF EB FC 练一练 (2)如果AB=10,AE=6,AF=5,那么FC的长是多少? A E B C F 解: ∵EF∥BC, ∴ ∵AB = 10 , AE = 6 , AF = 5. ∴ ∴FC=AC – AF = .AE AF EB FC 10 5 25.6 5 AB AFAC AE 1.如图,已知l1∥l2∥l3,下列比例式中错误的是( ) A. B. C. D. DF BD CE AC BF BD AE AC BF DF AE AC AC BD BF AE D A B C E D2、填空题: 如图:DE∥BC, 已知: 5 2 AC AE 则 . AB AD A B C D E 3.已知:DE//BC, AB=15,AC=9,BD=4 .求AE的长. 解:∵ DE∥BC, AB AC BD CE ∴ —— ——= .(推论) 即 15 9 ,4 12.5 12 29 11 .5 5 CE CE AE AC CE 1.平行线分线段成比例定理(基本事实) 两条直线被一组平行线所截,截得的对应线段成比例. 2.平行线分线段成比例定理的推论 推论1:平行于三角形一边的直线截其他两边(或两边的 延长线),所得的对应线段成比例. 推论2:平行于三角形的一边,并且和其他两边相交的 直线,所截得的三角形与原三角形的对应边成比例查看更多