- 2021-04-20 发布 |
- 37.5 KB |
- 2页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考理综全国卷Ⅰ第题的三种解法
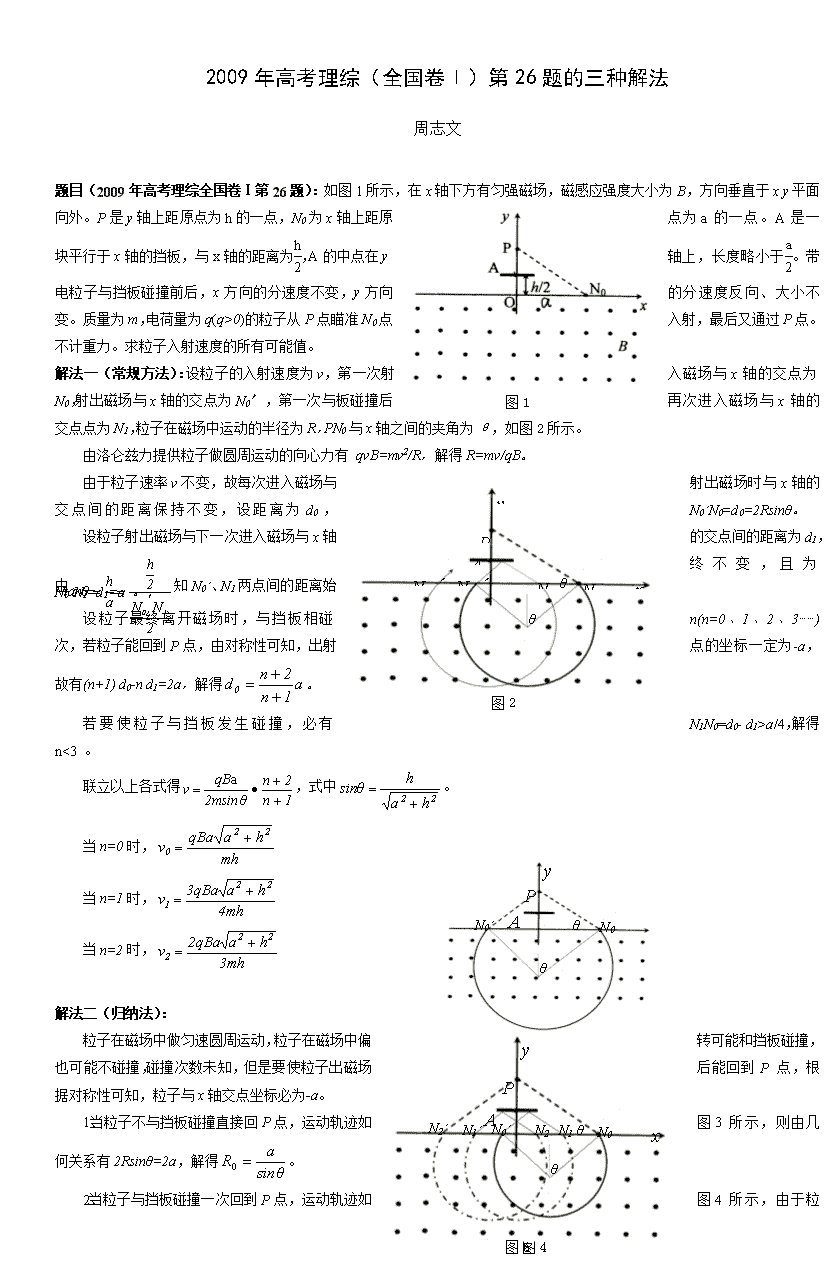
2009年高考理综(全国卷Ⅰ)第26题的三种解法 周志文 图1 题目(2009年高考理综全国卷Ⅰ第26题):如图1所示,在x轴下方有匀强磁场,磁感应强度大小为B,方向垂直于x y平面向外。P是y轴上距原点为h的一点,N0为x轴上距原点为a的一点。A是一块平行于x轴的挡板,与x轴的距离为,A的中点在y轴上,长度略小于。带电粒子与挡板碰撞前后,x方向的分速度不变,y方向的分速度反向、大小不变。质量为m,电荷量为q(q>0)的粒子从P点瞄准N0点入射,最后又通过P点。不计重力。求粒子入射速度的所有可能值。 解法一(常规方法):设粒子的入射速度为v,第一次射入磁场与x轴的交点为N0,射出磁场与x轴的交点为N0ˊ,第一次与板碰撞后再次进入磁场与x轴的交点点为N1,粒子在磁场中运动的半径为R,PN0与x轴之间的夹角为θ,如图2所示。 N1ˊ N1 N0 N0ˊ A y x P 图2 θ θ 由洛仑兹力提供粒子做圆周运动的向心力有 qvB=mv2/R,解得R=mv/qB。 由于粒子速率v不变,故每次进入磁场与射出磁场时与x轴的交点间的距离保持不变,设距离为d0, N0ˊN0=d0=2Rsinθ。 设粒子射出磁场与下一次进入磁场与x轴的交点间的距离为d1,由知N0ˊ、N1两点间的距离始终不变,且为N0ˊN1=d1=a 。 设粒子最终离开磁场时,与挡板相碰n(n=0、1、2、3……)次,若粒子能回到P点,由对称性可知,出射点的坐标一定为-a,故有(n+1) d0-n d1=2a,解得。 若要使粒子与挡板发生碰撞,必有N1N0=d0- d1>a/4,解得n<3 。 联立以上各式得,式中。 当n=0时, N0ˊ N0 y P A 图3 θ θ 当n=1时, 当n=2时, 解法二(归纳法): x y P A N1 N0ˊ N1ˊ N0 图4 θ θ 粒子在磁场中做匀速圆周运动,粒子在磁场中偏转可能和挡板碰撞,也可能不碰撞,碰撞次数未知,但是要使粒子出磁场后能回到P点,根据对称性可知,粒子与x轴交点坐标必为-a。 1、当粒子不与挡板碰撞直接回P点,运动轨迹如图3所示,则由几何关系有2Rsinθ=2a,解得。 N2 N2ˊ x y P A N1 N0ˊ N1ˊ N0 图5 θ θ 2、当粒子与挡板碰撞一次回到P 点,运动轨迹如图4所示,由于粒子速率v不变,故每次进入磁场与射出磁场两点间的距离不变,又由几何知识可知粒子每次射出磁场与下一次进入磁场两点间的距离也不变,且恒为a。根据几何关系可知,N1N0= N1ˊN0ˊ=a/2,N1N0ˊ=a,故2Rsinθ=3a/2, 解得。 y 图6 N0ˊ N3 x P A N1 N0ˊ N2ˊ N2 N3ˊ N1ˊ θ 3、当粒子与挡板碰撞二次回到P点,运动轨迹如图5所示,根据几何关系可知, N0ˊN1= N1ˊN2=a,N2ˊN1ˊ= N1ˊN0ˊ= N2N1= N1N0=a/3,故2Rsinθ=4a/3, 解得。 4、当粒子与挡板碰撞三次回到P点,运动轨迹如图6所示,根据几何关系可知,N2ˊN3= N1ˊN2= N0ˊN1=a,N3ˊN2ˊ= N2ˊN1ˊ= N1ˊN0ˊ= N3N1=N2N1= N1N0=a/4,故2Rsinθ=5a/4 解得。 如此类推,当粒子与挡板碰撞n次回到P点, 。又由R=mv/qB,解得: 当n=0时, 当n=1时, 当n=2时, …… 由于档板的长度略小于,因此要使粒子能与挡板碰撞,必须有N1N0>a/4,由以上分析知粒子只能与挡板碰撞两次,即n≤2。 解法三(极限法): 当粒子的速度最大时,它在磁场中运动时的圆轨迹的半径最大,但要回到P点,根据对称性,粒子经磁场偏转后与x轴交点的坐标为-a,此时粒子不与挡板碰撞(参考图3),由几何关系有2Rsinθ=2a,又由R=mv/qB,解得。 当粒子的速度最小时,它在磁场中运动时的圆轨迹的半径最小,与挡板碰撞次数最多(参考图6),虽然次数未知,但要与挡板碰撞,由以上分析必须有N1N0>a/4,因此它与挡板最多只能碰撞两次,可求得,。 查看更多