- 2021-04-20 发布 |
- 37.5 KB |
- 5页

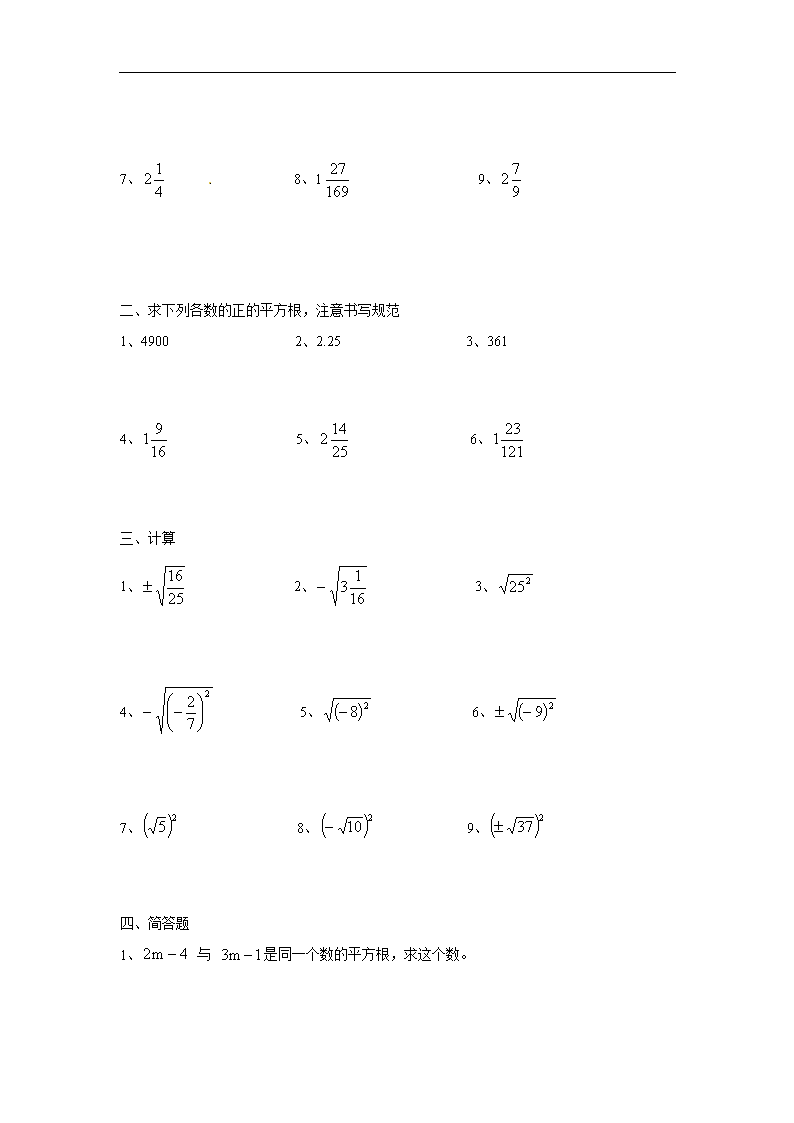

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
上海教育版数学七下《数的开方》同步练习2
12.2 平方根和开平方 一、课本巩固练习 一、填空题 1、______数有两个平方根,它们的和为______;零的平方根是______; ______数没有平方根 2、0.16 的平方根是_______ 3、 81 25 的算术平方根是_______ 4、81 的正的平方根的平方根是_______ 5、 81 的平方根是_______ 6、 25 的平方根是 ________ 7、 2 5 7 的平方根是_________[] 8、 6 是_______的一个平方根 9、_______的平方是 0.04 9、如果 2x =1.96,那么 x=________ 10、 1664 的平方根是_______ 11、一个正方形的面积是 5cm2,这个正方形的边长是________cm 12、如果 x =9,那么 x=_______ 13、 23 的算术平方根是______ 14、 56x 2 ,则 x=_________ 15、正数 k 的两个平方根的和是_________,积是________ 二、求下列各数的平方根,注意书写规范 1、16 2、0.01 3、121 4、0 5、256 6、0.0289 7、 4 12 8、1 169 27 9、 9 72 二、求下列各数的正的平方根,注意书写规范 1、4900 2、2.25 3、361 4、 16 91 5、 25 142 6、 121 231 三、计算 1、 25 16 2、 16 13 3、 225 4、 2 7 2 5、 28 6、 29 7、 2 5 8、 2 10 9、 2 37 四、简答题 1、 4m2 与 1m3 是同一个数的平方根,求这个数。 2、一个数的平方根 m、n 满足 2n3m4 ,求这个数。 3、当 m 为何值时, 6m2 有意义?当 m 为何值时, m266m2 有意义? 二、基础过关 一.选择题 1.下列说法中正确的有( ). ①只有正数才有平方根. ② 2 是 4 的平方根. ③ 16 的平方根是 4 . ④ 2a 的算术平方根是 a . ⑤ 2( 6) 的平方根是 6 .⑥ 9 3 . A.1 个 B.2 个 C.3 个 D.4 个 2.若 m = 40 -4,则估计 m 的值所在的范围是( ) A.1< m <2 B. 2< m <3 C. 3< m <4 D. 4< m <5 3. 试题下列说法中正确的是( ) A.4 是 8 的算术平方根 B.16 的平方根是 4 C. 6 是 6 的平方根 D.- a 没有平方根 4. 能使 x -3 的平方根有意义的 x 值是( ) A. x >0 B. x >3 C. x ≥0 D. x ≥3 5.有一个数值转换器,原理如下: 当输入的 x =64 时,输出的 y 等于( ) A.2 B.8 C.3 2 D. 2 2 6. 若 x , y 为实数,且| x +1|+ 1y =0,则 2013 x y 的值是( ) A.0 B.1 C.-1 D.-2011 二.填空题 7. 若 10404 102 ,则 1.0404 =__________. 8. 如果一个正方形的面积等于两个边长分别是 3 cm 和 5 cm 的正方 形的面积的和,则这个 正方形的边长为 ________.【 34 cm 】 9. 下列各数:81, 16 25 ,1.44, 12 4 , 81 的平方根分别是_______________;算术平方根 分别是_______________. 10.(1) 25 的平方根是________; (2) 25 的平方根是________,算术平方根是________; (3) 2x 的平方根是________,算术平方根是________; (4) 22x 的平方根是________,算术平方根是________. 【(1)±5;(2)±5;5;(3)± x ,| x |;(4)±( x +2),| x +2|;】 11.若实数 x y、 满足 21 ( 5)x + y = 0,则 yx 的值为 .【-1】 12. 若 ,则 ____________.【 】 三.解答题 13. x 为何值时,下列各式 有意义? (1) 2 ;x (2) ;x (3) 2 ;x (4) 1.x 【解:(1)2 x ≥0,解得 x ≥0; (2)- x ≥0,解得 x ≤0; (3) 2 0,x 解得 x 为一切实数; (4) x -1≥0,解得 x ≥1. 】 14.已知 1y 和 1 2x 互为相反数,且 0x ,求 y x 的值.【2】 15.如图,实数 a ,b 对应数轴上的点A 和 B,化简 2 2 2 2( ) ( )a b a b a b 【- a -b .】查看更多