德阳市2013年中考数学卷

德阳市2013年中考数学卷

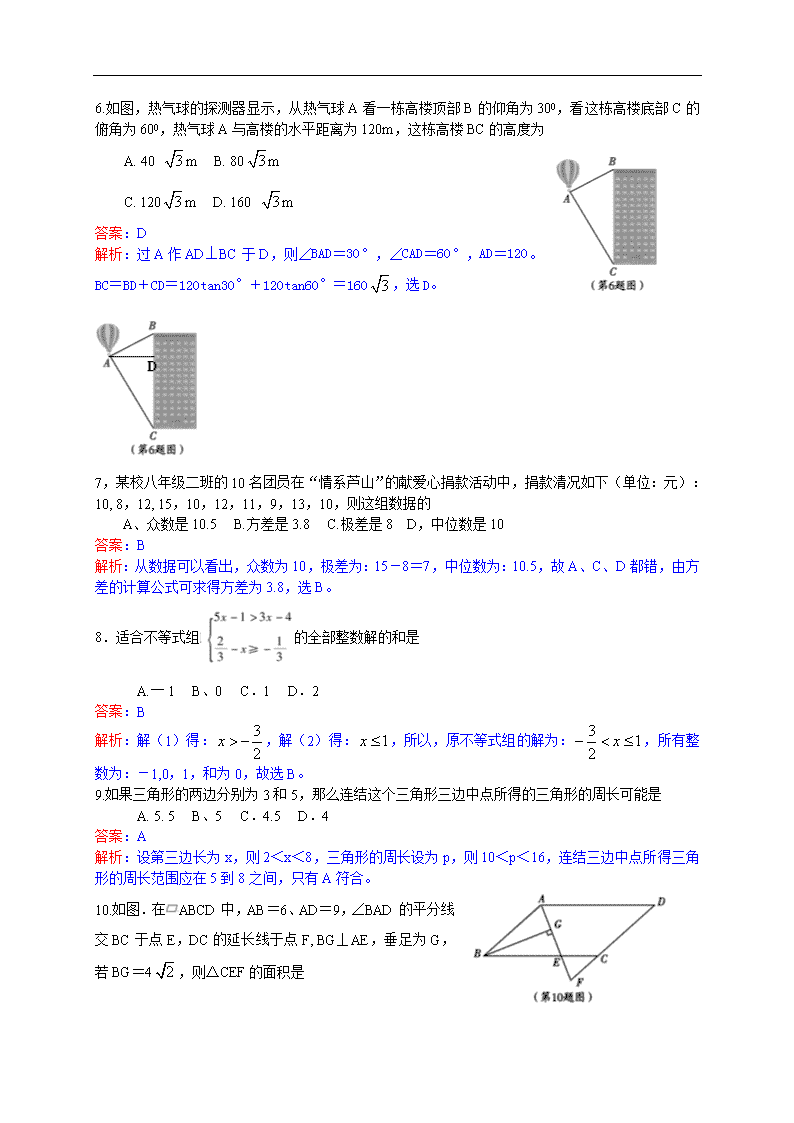
德阳市 2013 年初中毕业生学业考试与高中阶段学校招生考试 数学试卷（解析） 第 I 卷（选择，共 36 分） 一、选择题（本大共 12 个小，每小 3 分，共 36 分） 在每小题给出的四个选项中，有且仅有一项是符合题目要求的． 1 一 5 的绝对值是 A. 5 B. 　C. － 　D. －5 答案：A 解析：－5 的绝对值是它的相反数，所以，选 A。 2．已知空气的单位体积质量为 1.24×10－3 克/厘米 3，将 1.24×10－3 用小数表示为 A: 0. 000124　 B．0.0124 　C.一 0.00124 　D、0.00124 答案：D 解析：科学记数法的表示形式为 a×10n 的形式，其中 1≤|a|＜10，n 为整数．确定 n 的值时，要看把 原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值＞1 时， n 是正数；当原数的绝对值＜1 时，n 是负数。 1.24×10－3＝0.00124 3、如图，四个几何体分别为长方体、圆柱体、球体和三棱柱，这四个几何体中有三个的某一种视图 都是同一种几何图形，则另一个几何体是 答案：C 解析：长方体的三视图为矩形，只有二个视图一样，圆柱的正视图与侧视图为矩形，俯视图为圆， 三棱柱的正、侧视图为矩形，俯视图为三角形，只有球的三个视图都是圆。 4．下列计算正确的是 答案：B 解 析 ： ， ， ， 所 以，A、C、D 都错，只是 B 的计算是正确的。 5.如图．圆 O 的直径 CD 过弦 EF 的中点 G, ∠DCF=20°.，则∠EOD 等于 A. 10° 　　B. 20°　　C. 40° 　　D. 80° 答案：C 解析：因为直径过弦 EF 的中点 G，所以，CD⊥EF，且平分弧 EF，因此，弧 ED 与弧 BD 的度数都为 40°，所以，∠EOD＝40°，选 C。 1 5 1 5 2 2 2( ) 2a b a ab b− = − + 1 1 11a a a a a ÷ × = × = 2( 4) 4− = 6.如图，热气球的探测器显示，从热气球 A 看一栋高楼顶部 B 的仰角为 300，看这栋高楼底部 C 的 俯角为 600，热气球 A 与高楼的水平距离为 120m，这栋高楼 BC 的高度为 A. 40 m　 B. 80 m C. 120 m 　D. 160 m 答案：D 解析：过 A 作 AD⊥BC 于 D，则∠BAD＝30°，∠CAD＝60°，AD＝120。 BC＝BD＋CD＝120tan30°＋120tan60°＝160 ，选 D。 7，某校八年级二班的 10 名团员在“情系芦山”的献爱心捐款活动中，捐款清况如下（单位：元）： 10, 8，12, 15，10，12，11，9，13，10，则这组数据的 A、众数是 10.5　 B.方差是 3.8 　C.极差是 8　D，中位数是 10 答案：B 解析：从数据可以看出，众数为 10，极差为：15－8＝7，中位数为：10.5，故 A、C、D 都错，由方 差的计算公式可求得方差为 3.8，选 B。 8．适合不等式组 的全部整数解的和是 A.一 1 　B、0 　C．1 　D．2 答案：B 解析：解（1）得： ，解（2）得： ，所以，原不等式组的解为： ，所有整 数为：－1,0，1，和为 0，故选 B。 9.如果三角形的两边分别为 3 和 5，那么连结这个三角形三边中点所得的三角形的周长可能是 A. 5. 5 　B、5 　C．4.5 　D．4 答案：A 解析：设第三边长为 x，则 2＜x＜8，三角形的周长设为 p，则 10＜p＜16，连结三边中点所得三角 形的周长范围应在 5 到 8 之间，只有 A 符合。 10.如图．在 ABCD 中，AB＝6、AD＝9，∠BAD 的平分线 交 BC 于点 E，DC 的延长线于点 F, BG⊥AE，垂足为 G， 若 BG＝4 ，则△CEF 的面积是 3 3 3 3 3 3 2x > − 1x ≤ 3 12 x− < ≤ 2 　A、2 　　 B、 　C、3 　D、4 答案：A 解析：∵在▱ABCD 中，AB=CD=6，AD=BC=9，∠BAD 的平分线交 BC 于点 E， ∴∠BAF=∠DAF，∵AB∥DF，∠BAF=∠F，∴∠F=∠DAF， ∴△ADF 是等腰三角形，AD=DF=9；∵AB=CD=6， ∴CF=3； ∠BEA=∠DAF＝∠BAF，所以，BA＝BE， ∴在△ABG 中，BG⊥AE，AB=6，BG=4 　可得：AG=2， 又∵BG⊥AE，∴AE=2AG=4，∴△ABE 的面积等于 8 ， 又∵▱ABCD，∴△CEF∽△BEA，相似比为 1：2，面积 1：4，∴△CEF 的面积为,2 ． 11.为了了解我市 6000 名学生参加初中毕业会考数学考试的成绩情况，从中抽取了 200 名 考生的成绩进行统计，在这个问中，下列说法： ①这 6000 名学生的数学会考成绩的全体是总体；②每个考生是个体；③200 名考生是 总体的一个样本；④样本容量是 200，其中说法正确的有 A: 4 个　B. 3 个　C. 2 个　D: 1 个 答案：C 解析：每个考生的成绩是个体，故②错误，200 名考生的成绩是总体的一个样本，所以，③也错，① 和④正确，选 C＞ 12.如图，在圆 O 上有定点 C 和动点 P，位于直径 AB 的异侧，过点 C 作 CP 的垂线，与 PB 的延长 线交于点 Q，已知：圆 O 半径为 ，tan∠ABC＝ ，则 CQ 的最大值是 A、5　　　　B、 　　 C、 　　 D、 答案：D 解析：∵AB 为⊙O 的直径，∴∠ACB=90°， 在 Rt△PCQ 中，∠PCQ=∠ACB=90°，∵∠CPQ=∠CAB， ∴△ABC∽△PQC； 因为点 P 在⊙O 上运动过程中，始终有△ABC∽△PQC， ∴ ＝ ，AC、BC 为定值，所以 PC 最大时，CQ 取到最大值． ∵AB=5，tan∠ABC＝ ，即 BC：CA=4：3，所以，∴BC=4，AC=3． PC 的最大值为直线 5，所以， ，所以，CQ 的最大值为 2 2 2 2 2 2 2 5 2 3 4 15 4 25 3 20 3 BC CQ AC PC 3 4 4 3 5CQ = 20 3 德阳市 2013 年初中毕业生学业考试与高中阶段学校招生考试 第 II 卷（非选择，共 84 分） 二、填空题（每小 3 分，共 18 分，将答案填在答卡对应的号后的横线上） 13.从 1-9 这 9 个自然数中，任取一个，是 3 的倍数的概率是＿＿＿ 答案： 解析：3 的倍数为 3，6，9，共 3 个，所以，所求概率为： 14.已知一个多边形的每一个内角都等于 108°，则这个多边形的边数是＿＿＿ 答案：5 解析：因为每一个内角都为 108°，所以，每一个外角为 72°，边数为： ＝5。 15．已知关于 x 的方程 ＝3 的解是正数，则 m 的取值范围是＿＿＿＿ 答案：m＞－6 且 m≠－4 解析：去分母，得：2x＋m＝3x－6，解得：x＝m＋6，因为解为正数，所以，m＋6＞0，即 m＞－ 6， 又 x≠2，所以，m≠－4，因此，m 的取值范围为：m＞－6 且 m≠－4 16.用一个圆心角为 120°，半径为 4 的扇形作一个圆锥的侧面，这个圆锥的底面圆的半径是＿＿＿ 答案： 解析：扇形的周长为： ，所以 R＝ 17.若 ，则 ＝＿＿＿＿＿ 答案：6 解析：原方程变为： ，所以， ，由 得： ＝3，两边平方，得： ＝7，所以，原式＝7－1＝6 18.已知二次函数 y=ax2＋bx＋c ( 0)的图象如图所示，有下列 5 个 结论： ①abc＜0;　②b＜a＋c;　③4a＋2b+c>0 ④2c＜3b；⑤a＋b＜m (am＋b)（m≠1 的实数） 其中正确结论的序号有＿＿＿＿＿＿ 答案：①③④ 解析：由图象可知，a＜0，c＞0， ＞0，所以，b＞0，因此，abc ＜0，①正确；当 x＝－1 时，y＜0，所以，a－b＋c＜0，即 b＞a＋c， 所以，②错误；对于③，对称轴 ＝1，所以，b＝－2a，4a＋2b+c＝ 1 3 3 1 9 3 = 360 72 2 2 x m x + − 4 3 120 4 8 2180 3 R π π π× = = 4 3 2 23 1 2 1 0a a b b− + + − + = 2 2 1 | |a ba + − 2 23 1 ( 1) 0a a b− + + − = 2 3 1 0 1 a a b  − + =  = 2 3 1 0a a− + = 1a a + 2 2 1a a + a ≠ 2 b a − 2 b a − 4a－4a＋c，③正确；对于④ ④∵由①②知 b＝－2a 且 b＞a+c，所以，2b＞2a＋2c，∴2c＜3b，④正确； ⑤∵x=1 时，y=a+b+c（最大值），x＝m 时，y＝am2+bm+c， ∵m≠1 的实数，∴a+b+c＞am2+bm+c， ∴a+b＞m（am+b）成立．∴⑤错误 选①③④ 三、解答题（共 66 分解答应写出文字说明、证明过程或（推演步骤） 19．（7 分）计算：一 12013＋（ ）一 2 一｜3 一 ｜＋3tan60° 解析： 20，（10 分）为了了解学生对体育活动的喜爱情况，某校对参加足球、篮球、乒乓球、 羽毛球这四个课外活动小组的人员分布情况进行抽样调查，并根据收集的数据绘制了下面两 幅不完整的统计图，请根据图中提供的信息，解答下面问 （l）此次共调查了多少名同学？ （2）将条形统计图补充完整，并计算扇形统计图中的篮球部分的圆心角的度数。 (3）如果该校共有 1000 名学生参加这四个课外活动小组，而每个教师最多只能辅导本 组的 20 名学生，请通过计算确定每个课外活动小组至少需要准备多少名教师？ 解析： 1 2 27 21．（10 分）如图，直线 与双曲线 交于 C、D 两点，与 x 轴 交于点 A. (1)求 n 的取值范围和点 A 的坐标； （2)过点 C 作 CB⊥ Y 轴，垂足为 B，若 S △ABC＝4，求双曲线的解析式； (3）在（l）、(2）的条件卞，若 AB＝ ，求点 C 和点 D 的坐标并根据图象直接写出反比例 函数的值小于一次函数的值时，自变量 x 的取值范围． 解析： ( 0)y kx k k= + ≠ 1ny x += 17 22.（11 分）一项工程，甲队单独做需 40 天完成，若乙队先做 30 天后，甲、乙两队一 起合做 20 天恰好完成任务，请问： （1)乙队单独做需要多少天才能完成任务？ （2）现将该工程分成两部分，甲队做其中一部分工程用了 x 天，乙队做另一部分工程 用了 y 天，若 x; y 都是正整数，且甲队做的时间不到 15 天，乙队做的时间不到 70 天，那 么两队实际各做了多少天？ 解析： 23. (i4 分）如图，已知 AB 是圆 O 的直径，BC 是圆 O 的弦，弦 ED⊥AB 于点 F,交 BC 于点 G，过点 C 作圆 O 的切线与 ED 的延长线交于点 P． (1）求证：PC＝PG； （2）点 C 在劣弧 AD 上运动时，其他条件不变，若点 G 是 BC 的中点，试探究 CG、BF、BO 三 者之间的数量关系，并写出证明过程； （3）在满足（2）的条件下，已知圆为 O 的半径为 5,若点 O 到 BC 的距离为 时，求弦 ED 的 长． 解析： 5 24．（14 分）如图，在平面直角坐标系中有一矩形 ABCO（O 为原点），点 A、C 分别在 x 轴、y 轴上，且 C 点坐标为(0，6)，将△BCD 沿 BD 折叠(D 点在 OC 边上），使 C 点落 在 DA 边的 E 点上，并将△BAE 沿 BE 折叠，恰好使点 A 落在 BD 边的 F 点上． (1）求 BC 的长，并求折痕 BD 所在直线的函数解析式； （2）过点 F 作 FG⊥x 轴，垂足为 G，FG 的中点为 H，若抛物线 经过 B, H, D 三点，求抛物线解析式； (3）点 P 是矩形内部的点，且点 P 在（2）中的抛物线上运动（不含 B, D 点），过点 P 作 PN⊥BC，分别交 BC 和 BD 于点 N, M，是否存在这样的点 P，使 如果 存在，求出点 P 的坐标；如果不存在，请说明理由． 解析： 2y ax bx c= + +