- 2021-04-20 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
五年级上册数学教案-6平行四边形的面积|人教版 (21)
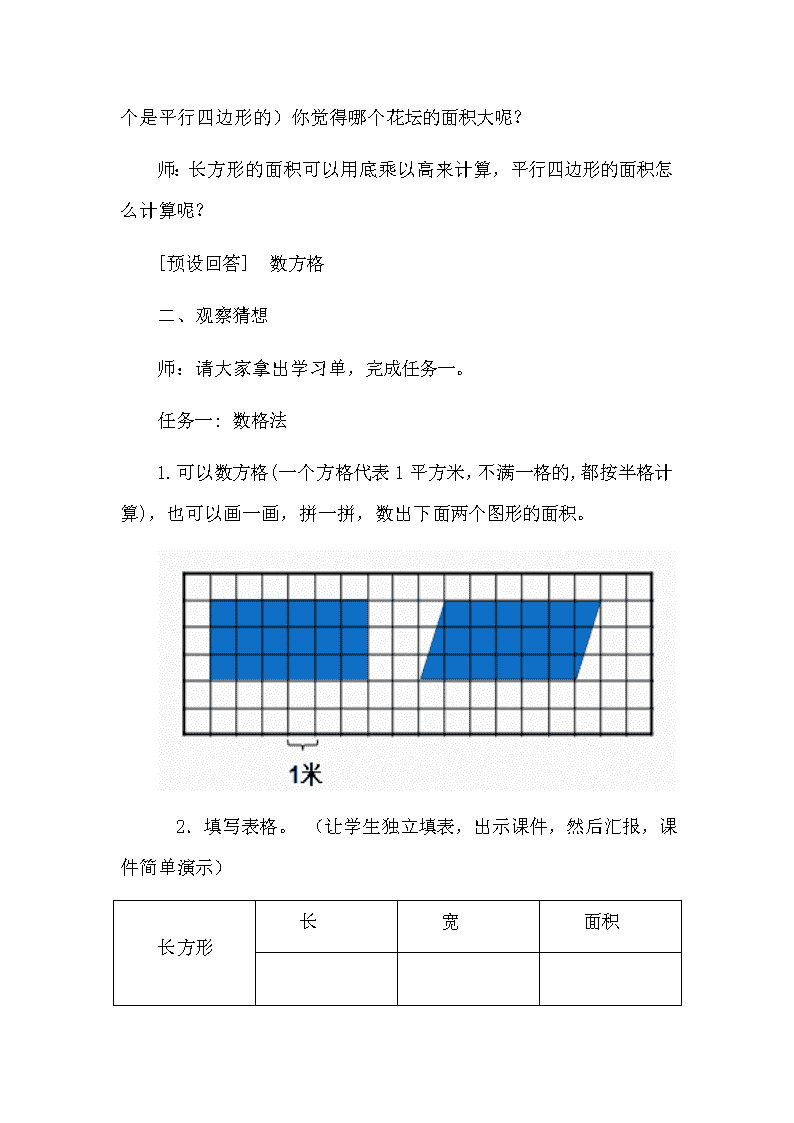
《平行四边形的面积》教学设计 教学内容:人教版教材五年级上册P87—88平行四边形的面积。 教学目标: 1.使学生通过数、剪、拼、算等实际操作,推导平行四边形的面积计算公式。 2.通过对图形的观察,比较和动手操作,发展学生的空间观念,渗透转化和平移的思想,并培养学生的分析,综合,抽象概括和动手解决实际问题的能力。 3.通过活动,激发学习兴趣,培养探索的精神,感受数学与生活的密切联系。 教学重点:理解平行四边形面积公式的推导过程,掌握平行四边形面积的计算方法。 教学难点:理解平行四边形面积公式的推导过程。 教学准备:课件、学习单、每4人小组一套学具(剪刀,直尺,带格子的平行四边形、平行四边形硬纸片等)。 教学过程: 一、激趣导入 师(出示主题图):你在图上发现了哪些平面图形? 师(抽取出学校门口的两个花坛的平面图,一个是长方形的,一个是平行四边形的)你觉得哪个花坛的面积大呢? 师:长方形的面积可以用底乘以高来计算,平行四边形的面积怎么计算呢? [预设回答] 数方格 二、观察猜想 师:请大家拿出学习单,完成任务一。 任务一: 数格法 1.可以数方格(一个方格代表1平方米,不满一格的,都按半格计算),也可以画一画,拼一拼,数出下面两个图形的面积。 2.填写表格。 (让学生独立填表,出示课件,然后汇报,课件简单演示) 长方形 长 宽 面积 平行四边形 底 高 面积 师:请观察表中的数据,你发现了什么? 师:根据刚才的发现,你能大胆猜想平行四边形的面积是怎样计算的吗?(揭示课题后让学生说自己的猜想) 三、动手操作,验证猜想 1.小组合作探究。 师:到底平行四边形的面积是不是用底乘高来计算呢?下面我们一起做个实验来验证这个猜想。请各小组拿出学习单,完成任务二。 任务二:剪一剪 移一移 拼一拼 每组同学手中都有两个完全相同的平行四边形纸片,可以选择其中的进操作。 在组长的组织下,利用学具进行操作实验,并解决下面三个问题。 (1)如何把平行四边形剪拼成长方形? (2)剪拼后面积有变化吗?拼出的长方形的长、宽与原来的平行四边形的底、高有什么关系? (3)你能根据长方形面积的计算公式推导出平行四边形的面积计算公式吗? 教师巡视,了解实验情况,指导展示小组进行操作和汇报。 2.组织学生进行学习成果汇报。 师:哪个小组愿意上来把你们的操作实验的过程和结果展示给全班同学们看? 按问题顺序让学生边操作边回答相关问题和完成板书,预设学生汇报如下。 生1:我们沿着平行四边形的高剪开,就把平行四边形分成了一个三角形和一个梯形,把三角形部分平移到梯形的另一边,就拼成了一个长方形。 生2:平行四边形拼成长方形后,只是把剪下部分移到了另一边,形状变了,但它们的面积并没有变化,是相等的。 生3:拼成的长方形的长和原来平行四边形的底相等,长方形的宽和平行四边形的高相等。 生4:根据“长方形的面积=长×宽”,我们就知道了“平行四边形的面积等于底×高”。) 3.质疑点拨 (1)质疑: 师:刚才这个小组同学的汇报真不错! 师:其他小组是不是也这样操作的呢?有没有不同的方法?(让有不同操作的同学上台展示) 师:从刚才这个的操作中我们可以发现,只要沿着平行四边形内的任意一条高剪开,都可以把平行四边形拼成一个长方形。 师:请同学们阅读课本88页,看看还有没有疑问?请大胆提出来。(如说出字母公式) (2)点拨: 师:刚才我们做了一个很成功的实验。 (课件演示)根据长方形的面积=长×宽,推导出了平行四边形的面积=底×高。如果用字母S表示平行四边形的面积,a表示底,h表示高,那么平行四边形面积的计算公式可以写成S=ah。从这个计算公式里我们知道要求平行四边形的面积必须要知道什么条件?(底和高) 四、测评提高 1.公式应用 出示例题:平行四边形花坛的底是6m,高是4m,它的面积是多少? (1)读题,分析已知条件和问题。 (2)独立完成。 (3)在黑板上展示并评析。 2、巩固练习 (1)判断 a.下面两图的面积都是6平方厘米。 ( ) 2厘米 2厘米 2厘米 3厘米 3厘米 b.下图面积是30×25=750(平方厘米)。 ( ) 25厘米 18厘米 30厘米 3、拓展练习 这几个平行四边形的面积相等吗? 小组合作交流,并汇报。 小结:等底等高的平行四边形面积相等。 五、课外延伸 刘徽的“割补术” 刘徽,被称作中国数学史上的牛顿,有着相当重要的历史地位。他著名的割补术解决了一个又一个的数学难题。用割补术系统地给出了各种图形面积公式的证明。 三角形、梯形的面积能否也利用“割补术”推导而来呢? 六、畅谈体会 同学们,说说你们这节课的收获和体会。 七、作业 把一个长方形拉成一个平行四边形,它的面积变了吗? 板书设计: 平行四边形的面积 长方形的面积 = 长 × 宽 平行四边形的面积 = 底 × 高 S = a h查看更多