福建省泉州市2020届高三上学期单科质量检查 数学（理）试题（PDF版）

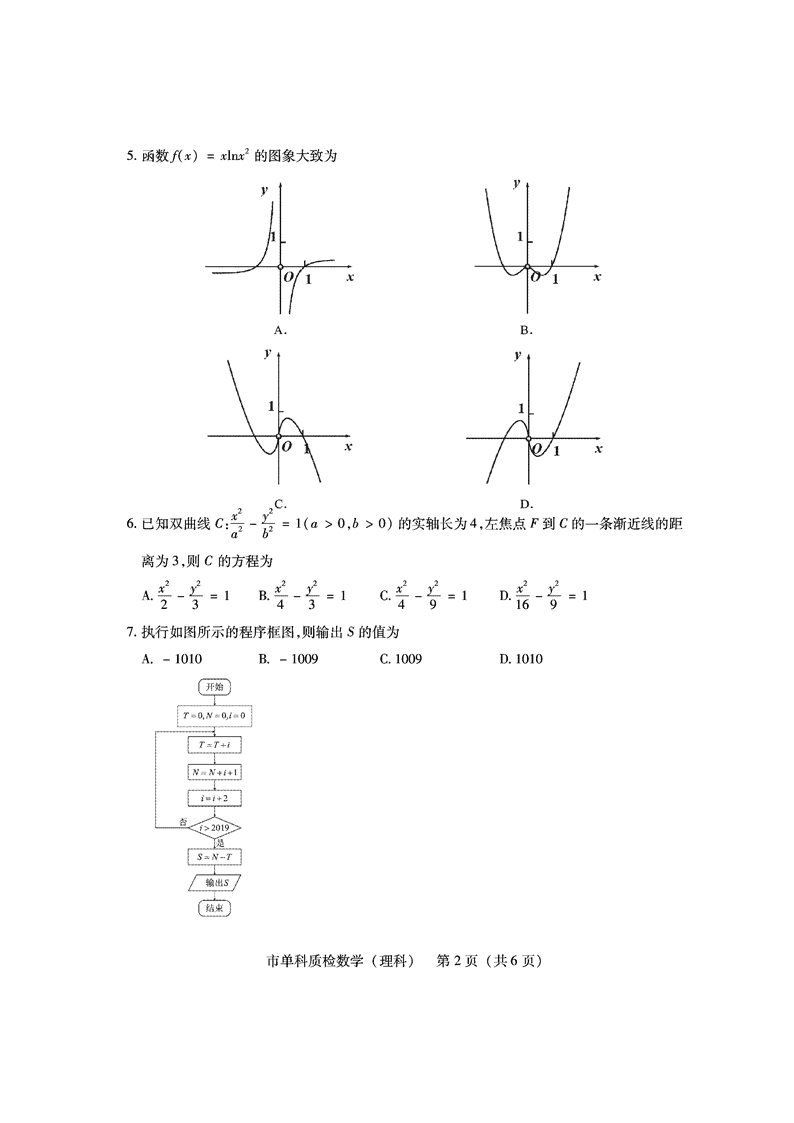
福建省泉州市2020届高三上学期单科质量检查 数学（理）试题（PDF版）

市单科质检数学（理科）试题 第 1 页（共 8 页） 保密★启用前 泉州市 2020 届高中毕业班单科质量检查 理 科 数 学 2020．1 注意事项： 1．答题前，考生先将自己的姓名、准考证号填写在答题卡上． 2．考生作答时，将答案答在答题卡上．请按照题号在各题的答题区域（黑色线框）内作答，超出答 题区域书写的答案无效．在草稿纸、试题卷上答题无效． 3．选择题答案使用 2B 铅笔填涂，如需改动，用橡皮擦干净后，再选涂其它答案标号；非选择题答案 使用 5.0 毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚． 4．保持答题卡卡面清洁，不折叠、不破损．考试结束后，将本试卷和答题卡一并交回． 一、选择题：本大题共 12 小题，每小题 5 分，共 60 分，在每小题给出的四个选项中，只有一项是符合题 目要求的． 1．已知集合  2 0M x x x   ，  1N x x  ，则 A． M N B． MN  C．  RM N D． M N   【解析】因为    2 0 0 1M x x x x x      ，  1N x x  ，所以 M N   ，故选 D． 2．若复数 z 满足 (1 i) 2 3i  z ，则 z A． 1 5 i2 2   B． 1 5 i2 2   C． 5 1 i2 2  D． 5 1 i2 2  【解析】由已知得 22 3i (2 3i)(1 i) 2 5i 3i 1 5i 1 i (1 i)(1 i) 2 2z             ，则 z 1 5 i2 2   ，故选 A． 3．若 x ， y 满足约束条件 2 0 3 1 0 2 x y x y y       ≤ ， ≥ ， ≤ ， 则 4 2z x y  的最小值为 A． 17 B． 13 C．16 3 D． 20 【解析】该可行域是一个以  1 3 7,2 , 4,2 , ,3 2 2A B C           为顶点的三角形区域(包括边界)．当动直线 2 2 zy x   过点 3 7,2 2C      时， z 取得最小值，此时 3 74 2 132 2z                  ，故选 B． 市单科质检数学（理科）试题 第 2 页（共 8 页） 4．已知 ,m n 是两条不同的直线， ,  是两个不重合的平面．给出下列四个命题： ①若  ， m ，则 m  ；②若 m n ， n ，则 m  ； ③若   ， m  ，则 m  ；④若 m  ， m ，则   ． 其中为真命题的编号是 A．①②④ B．①③ C．①④ D．②④ 【解析】①中，若  ，则  内任一直线与 平行，①为真命题． ②中，若 m n ， n ，则 m 可能平行于 ，也可能在 内，②为假命题． ③中，若   ，m  ，则 m 可能垂直于  ，也可能平行于  ，也可能与  相交但不垂直，③为 假命题． ④中，若 m  ，则可在 内作一直线 1m 使 1m m ，又因为 m ，所以 1m ，又 1m  ， 则   ，④为真命题． 综上，①④为真命题，故选 C． 5．函数 2( ) lnf x x x 的图象大致为 A． B． C． D． 市单科质检数学（理科）试题 第 3 页（共 8 页） 【解析】首先， 0x  ， ( )f x 为奇函数，排除 B；又 1 2 0e ef        ，排除 C； 当 0x  时， ( ) 2ln 2 0f x x    ，极值点 1 ex  ，排除 A；故选 D． 6．已知双曲线   2 2 2 2: 1 0, 0x yC a ba b     的实轴长为 4，左焦点 F 到C 的一条渐近线的距离为3 ，则C 的方程为 A． 2 2 12 3 x y  B． 2 2 14 3 x y  C． 2 2 14 9 x y  D． 2 2 116 9 x y  【解析】因为实轴长 42 a ，所以 2a ， )0,( cF  ，由对称性，双曲线的一个焦点到两条渐近线的距离 相等，不妨取渐近线为 xa by  ，即 0 aybx ，点 )0,( cF  到渐近线的距离 2 2 ( ) 0b c bcd bca b       ， 所以 3b ，所以C 的方程为 2 2 14 9 x y  ，故选 C． 7．执行如图所示的程序框图，则输出 S 的值为 A． 1010 B． 1009 C．1009 D．1010 【解析】依题意，得 2019531  N ， 0 2 4 6 2018T       ． 解法一： (1 0) (3 2) (5 4) (2019 2018) 1010S N T            ，故选 D． 解法二： 101010102 1010)20191( N ， (0 2018) 1010 1009 10102T     ， 所以 1010)10091010(10101009101010101010  TNS ，故选 D． 市单科质检数学（理科）试题 第 4 页（共 8 页） 8．明代朱载堉创造了音乐学上极为重要的“等程律”．在创造律制的过程中，他不仅给出了求解三项等 比数列的等比中项的方法，还给出了求解四项等比数列的中间两项的方法．比如，若已知黄钟、大吕、 太簇、夹钟四个音律值成等比数列，则有 = 大吕 黄钟 太簇 ，  23= 大吕 黄钟 夹钟 ，  23= 太簇 黄钟 夹钟 ．据此，可得正项等比数列 na 中， =ka A． 1 1 n kn k na a   B． 1 1 n kn k na a    C． 11 1 n k kn na a   D． 11 1 k n kn na a   【解析】解法一：因为 1 1 n na a q  ，所以 1 1 = nn aq a  ， 所以 1 11 1 = k nnk aa a a         1 1 1 1 = k n naa a        1 1 1 1= n k k n n na a     11 1= n k kn na a   ，故选 C． 解法二：（特值法）（具体略）． 9．已知抛物线 2: 8E x y 的焦点为 F ，过 F 的直线l 与 E 交于 ,A B 两点，与 x 轴交于点C ．若 A 为线 段CF 的中点，则 AB  A．9 B． 12 C． 18 D． 72 【解析】依题意得 4p ，焦点 )2,0(F ， 解法一：因为 A 为线段CF 的中点，所以 )1,22(A ， 4 2 )22(0 12   AFk ，所以直线 AF 的方 程 为 2 24y x  ， 将 其 代 入 yx 82  得 016222  xx ， 设 ),( 11 yxA ， ),( 22 yxB ， 则 2221  xx ， 4)(4 224 224 2 212121              xxxxyy 54224 2  ，所以 1 2 5 4 9AB y y p      ，故选 A． 解法二：（几何法）延长 BC 交准线 2y 于 D ，过点 A 作 AM 垂直准线交准线于 M ，过点 B 作 BN 垂直准线交准线于 N ，准线与 y 轴交于点 H ， FDH 中原点O 是线段 FH 的中点，所以点C 是线 段 DF 的中点．易得 4FH ， 3 ACAFAM ， 93  ACAD ，设 kBNBF  ，因 为 DMA DNB ∽ ， 所以 DB AD BN AM  ，即 kk  12 93 ，解得 6k ， 因此 963 AB ，故选 A． 市单科质检数学（理科）试题 第 5 页（共 8 页） 10．已知 πlog ea  ， πln eb  ， 2eln πc  ，则 A． a b c  B．b c a  C．b a c  D． c b a  【解析】因为 1b c  ，分别与中间量 1 2 做比较， 2 2 2 3 1 1 π 1 π(ln ln e) ln 02 2 e 2 eb      ， 4 3 2 2 1 1 e 1 e(ln ln e) ln 02 2 π 2 πc      ，则 1 2b c  ， 2 π π 1 1log e= log e2 2a   ， 1 1(2 ln π) ln π 2 0ln π ln πa c        ，所以 b c a  ，故选 B． 11．在平面直角坐标系 xOy 中，直线 : 4 0l kx y k   与曲线 29y x  交于 ,A B 两点，且 2AO AB    ， 则 k  A． 3 3 B． 2 2 C．1 D． 3 【解析】直线 04  kykx ，即 0)4(  yxk ，所以直线l 过定点 )0,4(P ，过圆心O 作 lOM  于 M ，即 1 22AO AB AM AB AB AB       ，所以 2AB ，曲线 29y x  是圆心为原点， 半径 3r 的上半圆． 解法一： Rt OAM 中， 1AM ， 3 OAr ，所以 22132 OM ， Rt OPM 中， 2 2 4 22sin MPO ，所以 4 πMPO ，直线l 的斜率为 14 πtan  ，故选 C． 解法二：圆心到直线l 的距离 1 4 )1( 4 222     k k k kd ， 2 1 4922 2 2 22         k kdrAB ，解得 1k ，故选 C． 12．已知正三棱柱 111 CBAABC  的所有棱长都为3 ，D 是 11CB 的中点，E 是线段 DA1 上的动点．若三棱 锥 ABCE  的四个顶点都在球O 的球面上，则球O 的表面积的取值范围为 A． 218π, π2      B． 27316π, π16      C． 273 π,21π16      D． 16π,21π 【解析】解法一：如图所示，依题意可知，三棱锥 ABCE  的外接球的球心 O 在上底面等边 1 1 1A B C 的 中心 1O 与下底面等边 ABC 的中心 2O 的连线的线段 1 2O O 上，设球O 的半径为 R ，当动点 E 在点 1A 位置时球O 的半径最大，此时球心O 在线段 1 2O O 的中点，在 2Rt AOO 中， 2 2 3 3 33 2O A     ， 市单科质检数学（理科）试题 第 6 页（共 8 页） 2 3O= 2O ，则球O 的半径 2 2 2 2 9 213 4 2R OA O A O O      ；当动点 E 在点 1O 位置时球O 的 半径最小，此时球心O 在线段 1 2O O 上，三棱锥 ABCE  为正三棱锥，在 2Rt AOO 中， 2 3O A  ， 2O=3O R ，由 2 2 2 2 2OA O A O O  得 2 2 2( 3) (3 R)R    解得 2R  ，所以 212 2R≤ ≤ ．由球 O 的表面积 24S R 得16π 21πS≤ ≤ ，故选 D． 解法二：如图所示，依题意可知，三棱锥 ABCE  的外接球的球心O 在上底面等边 1 1 1A B C 的中心 1O 与下底面等边 ABC 的中心 2O 的连线的线段 1 2O O 上，连接OA 、OE ，设OA OE R  ， 1O E x ， 1O O y ；在 1Rt OO E 中， 2 2 2 1 1OE O E O O  得 2 2 2R x y  ；在 2Rt AOO 中， 2 3AO  ， 2 =3OO R ， 由 2 2 2 2 2OA O A O O  得 2 2 23R y （ ） （3- ） ； 由 2 2 2R x y  和    2 22 3 3R y   得 2 2 2 23 =y x y （ ） （3- ） 整 理 得 2 12 6x y  ， 所 以 2 2 6 12R y y   2= 3y （ -3） ，又因为 0 3x≤ ≤ 得 3 22 y≤ ≤ ；当 2y  时， 2R 的最小值为 4 ； 当 3 2y  时， 2R 的最小值为 21 4 ；所以 2 214 4R≤ ≤ ，由球O 的表面积 24S R 得16π 21πS≤ ≤ ， 故选 D． 二、填空题：本题共 4 小题，每小题 5 分，共 20 分． 13．已知向量  ,2xa ，  2,1b ，且 a b ，则 =a ． 【解析】由 a b 得： 1 2 2 0x    ，即 4x  ，所以 2 2= 4 +2 = 20=2 5a ． 14．记 nS 为数列 na 的前 n 项和．若 12 0n na a   ， 5 93S  ，则 5a  ． 【解析】由 12 0n na a   得 1 1 2n na a  ，所以数列 na 是公比 1 2q  的等比数列， 市单科质检数学（理科）试题 第 7 页（共 8 页） 5 1 1 5 1(1 )(1 ) 32 9311 2 aa qS q    ，则 1 48a  ，故 4 5 1 3a a q   ． 15 ． 已 知 函 数  f x 是 定 义 在 R 上 的 奇 函 数 ， 当 0x  时 ， ( 1) 3 ( )f x f x  ； 当  0,1x 时 ， ( ) ln( 2)f x x  ，则  0 ( e)f f   ． 【解析】因为  f x 是定义在 R 上的奇函数，所以 ( e) (e)f f   ， (0) 0f  ， 又 2 e 3  ， 0 e 2 1   ，所以    (e) 9 e 2 9ln e 2 2 9f f      ，故  0 ( e) 9f f    ． 16．若函数    πsin 06f x x       在 π ,π2      单调，且在 π0, 3      存在极值点，则  的取值范围 为 ． 【解析】解法一：因为函数  f x 在 π ,π2      单调，则 π 2 2 T ≥ ，即 0 2 ≤ ． 当 π0, 3x     ， π π π π,6 6 3 6x       ，又  f x 在 π0, 3      存在极值点， π π 5π 3 6 6   ≤ ， 所以 π π π 3 6 2    ，则 1  ，1 2 ≤ ． 当 π ,π2x     ， π π π π, π6 2 6 6x         ，又 2π π π 7π 3 2 6 6   ≤ ， 7π π 13ππ6 6 6   ≤ ， 所以 π π π π 3π, π ,2 6 6 2 2              ，即 π π π+ ,2 6 2 π 3ππ+ ,6 2       ≥ ≤ 解得 2 4 3 3 ≤ ≤ ， 综上， 41 3  ≤ ． 解法二：因为函数  f x 在 π0, 3      存在极值点，所以 π π π 3 6 2    ，即 1  ． 当 π ,π2x     ， π π π π, π6 2 6 6x         ，又  f x 在 π ,π2      单调， 所以  π π π π 3π, π π, π2 6 6 +k +k k2 2               N ，即 π π π π,2 6 2 π 3ππ π,6 2 +k +k       ≥ ≤ 市单科质检数学（理科）试题 第 8 页（共 8 页） 解得 2 423 3k k ≤ ≤ ，只能取 0k  ，即 2 4 3 3 ≤ ≤ ． 综上， 41 3  ≤ ． 市单科质检数学（理科）试题 第 1 页（共 11 页） 保密★启用前 泉州市 2020 届高中毕业班单科质量检查 理 科 数 学 2020．1 注意事项： 1．答题前，考生先将自己的姓名、准考证号填写在答题卡上． 2．考生作答时，将答案答在答题卡上．请按照题号在各题的答题区域（黑色线框）内作答，超出答 题区域书写的答案无效．在草稿纸、试题卷上答题无效． 3．选择题答案使用 2B 铅笔填涂，如需改动，用橡皮擦干净后，再选涂其它答案标号；非选择题答案 使用 5.0 毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚． 4．保持答题卡卡面清洁，不折叠、不破损．考试结束后，将本试卷和答题卡一并交回． 三、解答题：共 70 分．解答应写出文字说明、证明过程或演算步骤．第 17~21 题为必考题，每个试题考 生都必须作答．第 22、23 题为选考题，考生根据要求作答． （一）必考题：共 60 分． 17．（12 分） 如图，四棱锥 ABCDP  的底面是正方形， PA 平面 ABCD ， AE PD ． （1）证明： AE  平面 PCD ； （2）若 AP AB ，求二面角 DPCB  的余弦值． 【命题意图】本小题考查线面垂直的判定与性质、二面角的求解及空间向量的坐标运算等基础知识，考查 空间想象能力、逻辑推理及运算求解能力，考查化归与转化思想、函数与方程思想等，体现 基础性、综合性与应用性，导向对发展数学抽象、逻辑推理、直观想象等核心素养的关注． 【试题解析】 解法一：（1）因为 PA  平面 ABCD ，CD  平面 ABCD ， 市单科质检数学（理科）试题 第 2 页（共 11 页） 所以 PA CD ．·········································································································1 分 又底面 ABCD 是正方形，所以 AD CD ．····································································· 2 分 又 PA AD A ，所以 CD  平面 PAD ．······································································3 分 又 AE  平面 PAD ，所以CD AE ．··········································································· 4 分 又因为 AE PD ，CD PD D ， ,CD PD  平面 PCD ，············································· 5 分 所以 AE  平面 PCD ．······························································································· 6 分 （2）因为 PA  平面 ABCD ，底面 ABCD 为正方形， 所以 PA AB ， PA AD ， AB AD ，分别以 AB 、 AD 、 AP 所在的直线为 x 轴、 y 轴、 z 轴 建立空间直角坐标系 A xyz （如图所示）．······································································7 分 设 1PA AB  ，则 A 0,0,0（ ）， B 1,0,0（ ），C 1,1,0（ ）， D 0,1,0（ ）， (0,0,1)P ， 1 1(0, , )2 2E ， 1,0, 1PB   （ ）， 1,1, 1PC   （ ）， 1 1(0, , )2 2AE  ．··························································8 分 由（1）得 1 1(0, , )2 2AE  为平面 PCD 的一个法向量．·······················································9 分 设平面 PBC 的一个法向量为 1 1 1( )m x ,y ,z ． 由 0, 0, PB m PC m          得 1 1 1 1 1 0, 0, x z x y z       令 1 1x  ，解得 1 1z  ， 1 0y  ． 所以 (1,0,1)m  ．····································································································· 10 分 因此 1 12cos , 212 2 m AEm AE m AE           ．······························································· 11 分 由图可知二面角 B PC D  的大小为钝角． 故二面角 B PC D  的余弦值为 1 2  ．········································································· 12 分 解法二：（1）同解法一．·····································································································6 分 （2）过点 B 作 BF 垂直于 PC 于点 F ，连接 DF 、 BD ． 因为 PB PD ， BC CD ， PC PC ， 所以 PBC PDC△ ≌△ ．······························································································ 7 分 因此易得 090DFC BFC    ， BF DF ．································································8 分 所以 BFD 为二面角 B PC D  的平面角．··································································· 9 分 设 1PA AB  ，则 2BD  ， 6 3BF DF  ．························································· 10 分 市单科质检数学（理科）试题 第 3 页（共 11 页） 在 BDF△ 中，由余弦定理，得 2 2 2 2 2 2 2 6 6( ) ( ) ( 2) 13 3cos 2 262 ( )3 BF DF BDBFD BF DF         ． 故二面角 B PC D  的余弦值为 1 2  ．········································································· 12 分 18．（12 分） 记 nS 为数列 na 的前 n 项和．已知 0na  ， 26 3 4n n nS a a   ． （1）求 na 的通项公式； （2）设 2 2 1 1 n n n n n a ab a a    ，求数列 nb 的前 n 项和 nT ． 【命题意图】本小题主要考查递推数列、等差数列的通项公式与数列求和等基础知识，考查推理论证能力 与运算求解能力等，考查化归与转化思想、特殊与一般思想等，体现基础性，导向对发展逻 辑推理、数学运算等核心素养的关注． 【试题解析】 解：（1）当 1n  时， 2 1 1 16 3 4S a a   ，所以 1 4a  或 1 （不合，舍去）．································1 分 因为 26 3 4n n nS a a   ①，所以当 2≥n 时， 2 1 1 16 3 4n n nS a a     ②， 由①  ②得 2 2 1 16 3 3n n n n na a a a a     ，······································································2 分 所以  1 1 3 0n n n na a a a     ．················································································3 分 又 0na  ，所以 1 3n na a   ．······················································································ 4 分 因此 na 是首项为 4 ，公差为3 的等差数列．···································································5 分 故  4 3 1 3 1na n n     ．························································································6 分 （2）由（1）得        2 23 1 3 4 3 323 1 3 4 3 1 3 4n n nb n n n n          ，········································ 9 分 所以   3 3 3 3 3 3 92 ( ) 24 7 7 10 3 1 3 4 4 3 4n nT n nn n n            ．···························· 12 分 19．（12 分） ABC△ 中， 60B  ， 2AB  ， ABC△ 的面积为 2 3 ． （1）求 AC ； （2）若 D 为 BC 的中点， ,E F 分别为 ,AB AC 边上的点（不包括端点），且 120EDF   ，求 DEF△ 面积的最小值． 市单科质检数学（理科）试题 第 4 页（共 11 页） 【命题意图】本小题主要考查解三角形、三角恒等变换等基础知识，考查推理论证能力和运算求解能力等， 考查数形结合思想和化归与转化思想等，体现综合性与应用性，导向对发展直观想象、逻辑 推理、数学运算及数学建模等核心素养的关注． 【试题解析】 解法一：（1）因为 60B  ， 2AB  ， 所以 1 sin2ABCS AB BC B   △ 1 322 2 BC    3 2 BC ，·············································2 分 又 2 3ABCS △ ，所以 4BC  ．··················································································· 3 分 由余弦定理，得 2 2 2 2 cosAC AB BC AB BC B     ······················································· 4 分 2 2 12 4 2 2 4 2       12 ，························································································· 5 分 所以 2 3AC  ．········································································································6 分 （2）设 BDE   ，  0 ,60    ，则 60CDF    ． 在 BDE△ 中，由正弦定理，得 sin sin BD DE BED B  ，·························································7 分 即 2 sin(60 ) 3 2 DE   ，所以 3 sin(60 )DE   ；··························································· 8 分 在 CDF△ 中，由正弦定理，得 sin sin CD DF CFD C  ， 由（1）可得 30C  ，即 2 1sin(90 ) 2 DF   ，所以 1 cosDF  ；····································· 9 分 所以 1 sin2DEFS DE DF EDF    △ 3 4sin(60 ) cos    2 3 2 3 cos 2sin cos      ········································································10 分   3 2sin 2 60 3     ，············································································11 分 当 15   时，sin(2 60 ) 1    ， min 3( ) 6 3 3 2 3DEFS    △ ． 故 DEF△ 面积的最小值为 6 3 3 ．············································································12 分 市单科质检数学（理科）试题 第 5 页（共 11 页） 解法二：（1）同解法一．·····································································································6 分 （2）设 CDF   ，  0 ,60    ，则 60BDE    ． 在 CDF△ 中，由正弦定理，得 sin sin CD DF CFD C  ，························································ 7 分 由（1）可得 30C  ，即 2 1sin(30 ) 2 DF   ，所以   1 sin 30DF   ；··························· 8 分 在 BDE△ 中，由正弦定理，得 sin sin BD DE BED B  ， 即 2 sin(120 ) 3 2 DE   ，所以 3 sin(120 )DE   ；························································· 9 分 所以 1 sin2DEFS DE DF EDF    △   3 3 4 sin 30 sin(120 )      3 1 3 3 14 cos sin cos sin2 2 2 2                   ··············································· 10 分 3 2sin 2 3   ，······················································································ 11 分 当 45   时，sin 2 1  ， min 3( ) 6 3 3 2 3DEFS    △ ． 故 DEF△ 面积的最小值为 6 3 3 ．············································································12 分 20．（12 分） 已知椭圆 2 2 2 2: 1( 0)x yE a ba b     的离心率为 1 2 ，点 3( 3, )2A 在 E 上． （1）求 E 的方程； （2）斜率不为 0 的直线 l 经过点 1( ,0)2B ，且与 E 交于 QP, 两点，试问：是否存在定点 C ，使得 QCBPCB  ？若存在，求 C 的坐标；若不存在，请说明理由． 【命题意图】本小题主要考查椭圆的几何性质、直线与椭圆的位置关系等基础知识，考查推理论证能力、 运算求解能力等，考查化归与转化思想、数形结合思想、函数与方程思想等，体现基础性、 综合性与创新性，导向对发展逻辑推理、直观想象、数学运算、数学建模等核心素养的关注． 【试题解析】 市单科质检数学（理科）试题 第 6 页（共 11 页） 解法一：（1）因为椭圆 E 的离心率 2 2 1 2 a be a   ，所以 2 23 4a b ①，·································· 1 分 点 )2 3,3(A 在椭圆上，所以 14 33 22  ba ②，······························································· 2 分 由①②解得 42 a ， 32 b ．························································································ 3 分 故 E 的方程为 134 22  yx ．··························································································4 分 （2）假设存在定点C ，使得 PCB QCB   ． 由对称性可知，点C 必在 x 轴上，故可设 ( ,0)C m ．·························································· 5 分 因为 PCB QCB   ，所以直线 PC 与直线QC 的倾斜角互补，因此 0PC QCk k  ．·············6 分 设直线l 的方程为： 2 1 tyx ， ),( 11 yxP ， ),( 22 yxQ ． 由 2 2 1 ,2 14 3 x ty x y       消去 x ，得 04512)1612( 22  tyyt ，··············································· 7 分 2 2 2 2(12 ) 4 (12 16) ( 45) 144 180 (12 16) 0t t t t            ，所以t R ， 1 2 2 12 12 16 ty y t     ， 1 2 2 45 12 16y y t    ，····································································8 分 因为 0 QCPC kk ，所以 0 2 2 1 1  mx y mx y ， 所以 0)()( 1221  mxymxy ，即 0)2 1()2 1( 1221  mtyymtyy ．························· 9 分 整理得 1 2 1 2 12 ( )( ) 02ty y m y y    ， 所以 01612 12)2 1()1612 45(2 22   t tmtt ，即 01612 )12)(2 1(90 2   t tmt ．················· 10 分 所以 0)2 1(1290  mtt ，即 0)]2 1(1290[  tm ，对t R 恒成立， 即 0)1296(  tm 对t R 恒成立，所以 8m ．·····························································11 分 所以存在定点 )0,8(C ，使得 QCBPCB  ．·······························································12 分 解法二：（1）同解法一．·····································································································4 分 （2）若点C 存在，当直线 PQ 垂直 x 轴时，点C 必在 x 轴上， 市单科质检数学（理科）试题 第 7 页（共 11 页） 如果直线 PQ 不垂直 x 轴，由对称性可知，点C 也必在 x 轴上．··········································· 5 分 假设存在点 )0,(mC ，使得 QCBPCB  ，即直线 PC 与直线QC 的倾斜角互补， 所以 0 QCPC kk ．····································································································6 分 设直线l 的方程为 )2 1(  xky ， ),( 11 yxP ， ),( 22 yxQ ． 由 2 2 1( ),2 14 3 y k x x y       消去 x ，得 0124)34( 2222  kxkxk ，·········································· 7 分 2 2 2 2 2( 4 ) 4 (4 3)( 12) 180 144 0k k k k          ，所以 kR， 2 1 2 2 4 4 3 kx x k    ， 34 12 2 2 21   k kxx ，··············································································8 分 因为 0 QCPC kk ，所以 0 2 2 1 1  mx y mx y ，所以 0)()( 1221  mxymxy ，················ 9 分 即 1 2 2 1 1 1( )( ) ( )( ) 02 2k x x m k x x m      ． 整理得 0]))(2 1(2[ 2121  mxxmxxk ，·································································· 10 分 所以 0]34 4)2 1(34 242[ 2 2 2 2   mk kmk kk ， 整理得 034 243 2   k mk ，对任意的 kR恒成立，···························································· 11 分 所以 8m ，故存在 x 轴上的定点 )0,8(C ，使得 QCBPCB  ．····································12 分 21．（12 分） 已知函数  2( ) 1 e xf x x ax   ． （1）讨论 ( )f x 的单调性； （2）若函数  2( ) 1 e 1xg x x mx    在 1,  有两个零点，求 m 的取值范围． 【命题意图】本小题主要考查导数的综合应用，利用导数研究函数的单调性、最值和零点等问题，考查抽 象概括、推理论证、运算求解能力，考查应用意识与创新意识，综合考查化归与转化思想、 分类与整合思想、函数与方程思想、数形结合思想、有限与无限思想以及特殊与一般思想， 考查数学抽象、逻辑推理、直观想象、数学运算、数学建模等核心素养． 【试题解析】 市单科质检数学（理科）试题 第 8 页（共 11 页） 解：（1）因为  2( ) 1 e xf x x ax   ，所以  2( ) 2 1 e xf x x a x a        ，··························· 1 分 即   ( ) 1 1 e xf x x a x     ． 由 ( ) 0f x  ，得  1 1x a   ， 2 1x   ．······································································2 分 ①当 0a  时，  2( ) 1 e 0xf x x   ≥ ，当且仅当 1x   时，等号成立． 故 ( )f x 在 ,  为增函数．·····················································································3 分 ②当 0a  时，  1 1a    ， 由 ( ) 0f x  得  1x a   或 1x   ，由 ( ) 0f x  得  1 1a x     ； 所以 ( )f x 在   , 1a   ， 1,+  为增函数，在   1 , 1a   为减函数．····················· 4 分 ③当 0a  时，  1 1a    ， 由 ( ) 0f x  得  1x a   或 1x   ，由 ( ) 0f x  得  1 1x a     ； 所以 ( )f x 在 , 1  ，   1 ,+a   为增函数，在   1, 1a   为减函数．······················5 分 综上，当 0a  时， ( )f x 在 ,  为增函数； 当 0a  时， ( )f x 在   , 1a   ， 1,+  为增函数，在   1 , 1a   为减函数； 当 0a  时， ( )f x 在 , 1  ，   1 ,+a   为增函数，在   1, 1a   为减函数． （2）因为  2( ) 1 e 1xg x x mx    ，所以  2( ) 1 e xg x x m    ， ①当 0m≤ 时， ( ) 0g x ≥ ， ( )g x 在 1,  为增函数，所以 ( )g x 在 1,  至多一个零点．··· 6 分 ②当 0m  时，由（1）得 ( )g x 在 1,  为增函数． 因为 (0) 1g m   ， (0) 0g  ． （i）当 =1m 时， (0) 0g  ， 0x  时， ( ) 0g x  ， 1 0x   时， ( ) 0g x  ； 所以 ( )g x 在 1,0 为减函数，在 0, 为增函数，  min( ) 0 0g x g  ． 故 ( )g x 在 1,  有且只有一个零点．···········································································7 分 （ii）当 >1m 时， (0) 0g  ，  2( ) 1 0mg m m e m     ，  0 0,x m  ，使得  0 0g x  ， 且 ( )g x 在 01, x 为减函数，在 0 ,x  为增函数． 市单科质检数学（理科）试题 第 9 页（共 11 页） 所以  0( ) 0 0g x g  ，又      2 2 2 21 e 1 1 1 0mg m m m m m         ， 根据零点存在性定理， ( )g x 在 0 ,x m 有且只有一个零点．·················································8 分 又 ( )g x 在 01, x 上有且只有一个零点 0 ． 故当 >1m 时， ( )g x 在 1,  有两个零点．····································································9 分 （iii）当 0 <1m 时， ( 1) 0g m     ， (0) 0g  ，  0 1,0x   ，使得  0 0g x  ， 且 ( )g x 在 01, x 为减函数，在 0 ,x  为增函数． 因为 ( )g x 在 0 ,x  有且只有一个零点 0 ， 若 ( )g x 在 1,  有两个零点，则 ( )g x 在 01, x 有且只有一个零点．······························10 分 又  0( ) 0 0g x g  ，所以  1 0g  ≥ 即   21 1 0eg m    ≥ ，所以 21 em ≥ ， 即当 21 1e m ≤ 时， ( )g x 在 1,  有两个零点．·······················································11 分 综上， m 的取值范围为  21 ,1 1,e      ．··································································12 分 （二）选考题：共 10 分．请考生在第 22、23 两题中任选一题作答．如果多做，则按所做的第一题计分． 22．[选修 4 4 ：坐标系与参数方程]（10 分） 在同一平面直角坐标系 xOy 中，经过伸缩变换 2 ,x x y y      后，曲线 2 2 1 : 1C x y  变为曲线 2C ． （1）求 2C 的参数方程； （2）设  2,1A ， P 是 2C 上的动点，求 OAP△ 面积的最大值，及此时 P 的坐标． 【命题意图】本小题主要考查圆的直角坐标方程与极坐标方程的互化，直线的参数方程及参数的几何意义、 直线与圆的位置关系等基础知识，考查推理论证能力与运算求解能力，考查函数与方程思想、 转化与化归思想、数形结合思想，体现基础性与综合性，导向对发展直观想象、逻辑推理、 数学运算等核心素养的关注． 【试题解析】 解法一：（1）由伸缩变换 2 ,x x y y      得到 1 ,2 . x x y y     ……①··························································1 分 将①代入 2 2 1x y  ，得到 2 21 + =12 x y （ ） ，整理得 2C ： 2 2+ =14 x y  ．··································· 3 分 市单科质检数学（理科）试题 第 10 页（共 11 页） 所以 2C 的参数方程为 2cos , sin x y      （为参数 ）．····························································5 分 （2）设   2cos ,sin 0 2πP    ≤ ，直线 : 2 0OA x y  ，········································· 6 分 则 P 到直线OA 的距离为 π2 2 cos2cos 2sin 4 5 5 d         ，··································7 分 所以 1 1 1 2 25 5 22 2 2 5OAPS OA d d       △ ≤ ．···················································8 分 当且仅当 3= 4  或 7= 4  时， OAP△ 的面积的最大值为 2 ，··········································9 分 此时 P 22, 2      或 22, 2      ．············································································ 10 分 解法二：（1）同解法一．·····································································································5 分 （2）直线 : 2 0OA x y  ，设直线 l ： 2 0x y c   ．···················································· 6 分 联立 2 2 2 0 +y 14 x y c x     ， ， 消去 y ，得到 2 22 2 4 0x cx c    ，···············································7 分 令 =0 ，得  2 24 8 4 0c c   ，解得 2 2c   ．·························································· 8 分 此时解得 2, 2 2 x y     或 2, 2 ,2 x y     即 1 2( 2, )2P  或 2 2( 2, )2P  ．·································9 分 这时 1P ， 2P 到直线OA 的距离均为 2 2 5 ，所以 max 1 2 25 22 5OAPS    △ ．·············· 10 分 23．[选修 4 5 ：不等式选讲]（10 分） 已知函数 1( ) | | | |f x x a x a     ． （1）证明： ( ) 2f x ≥ ； （2）当 1 2a  时， ( )f x x b≥ ，求b 的取值范围． 【命题意图】本小题主要考查绝对值不等式的解法、不等式解集的概念、绝对值的意义等基础知识，考查 抽象概括能力、运算求解能力，考查分类与整合的思想，转化与化归的思想，体现基础性与 综合性，导向对发展逻辑运算、数学运算、直观想象等核心素养的关注． 【试题解析】 市单科质检数学（理科）试题 第 11 页（共 11 页） 解法一：（1） 1 1 1 1( ) | | | | | | | | | | 2 | | | | 2f x x a x a a aa a a a         ≥ ≥ ．····························5 分 （2） 3 12 , ,2 2 1 5 1( ) 2 = , 2,2 2 2 32 , 2,2 x x f x x x x x x              ≤ 　 ≥ ······························································8 分 作出 ( )f x 的图象，如图： ·······················································9 分 将 52 2A（ ，）代入 y x b  得到 1 2b  ，由图可得b 的取值范围为 1( , ]2  ．····························10 分 解法二：（1）同解法一．·····································································································5 分 （2）令   ( )g x f x x  ，所以 min( )b g x≤ ．·································································· 6 分 3 13 , ,2 2 1 5 1( ) 2 = , 2,2 2 2 3 , 2,2 x x g x x x x x x x x                 ≤ 　 ≥ ····························································· 8 分 可得 ( )g x 在 ,2 单调递减，在 2  ， 单调递增，所以    min 1= 2 2g x g  ，···················9 分 所以b 的取值范围为 1, 2     ．····················································································10 分 A