- 2021-04-19 发布 |
- 37.5 KB |
- 7页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
上海教育高中数学三上空间直线与直线的位置关系一
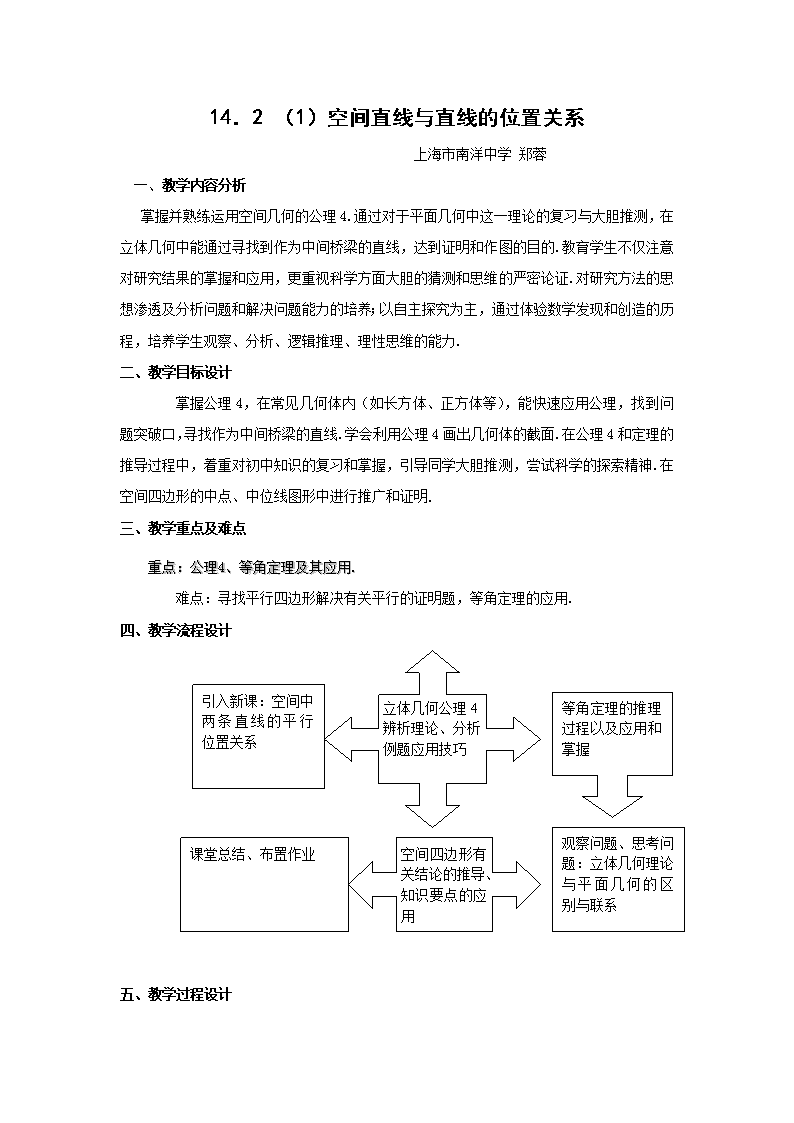
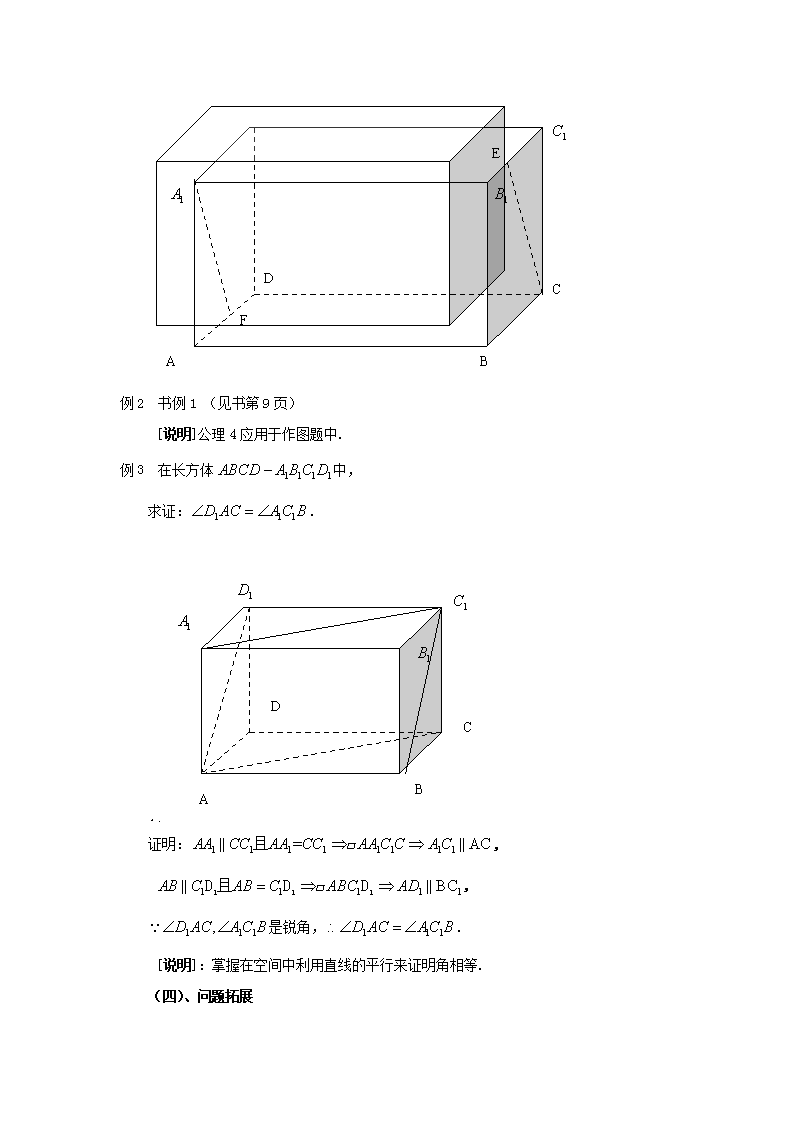
14.2 (1)空间直线与直线的位置关系 上海市南洋中学 郑蓉 一、教学内容分析 掌握并熟练运用空间几何的公理4.通过对于平面几何中这一理论的复习与大胆推测,在立体几何中能通过寻找到作为中间桥梁的直线,达到证明和作图的目的.教育学生不仅注意对研究结果的掌握和应用,更重视科学方面大胆的猜测和思维的严密论证.对研究方法的思想渗透及分析问题和解决问题能力的培养;以自主探究为主,通过体验数学发现和创造的历程,培养学生观察、分析、逻辑推理、理性思维的能力. 二、教学目标设计 掌握公理4,在常见几何体内(如长方体、正方体等),能快速应用公理,找到问题突破口,寻找作为中间桥梁的直线.学会利用公理4画出几何体的截面.在公理4和定理的推导过程中,着重对初中知识的复习和掌握,引导同学大胆推测,尝试科学的探索精神.在空间四边形的中点、中位线图形中进行推广和证明. 三、教学重点及难点 重点:公理4、等角定理及其应用. 难点:寻找平行四边形解决有关平行的证明题,等角定理的应用. 四、教学流程设计 空间四边形有关结论的推导、知识要点的应用 立体几何公理4 辨析理论、分析例题应用技巧 引入新课:空间中两条直线的平行位置关系 等角定理的推理过程以及应用和掌握 观察问题、思考问题:立体几何理论与平面几何的区别与联系 课堂总结、布置作业 五、教学过程设计 一、引入课题 从生活实例中寻找空间中平行的传递性.. 二、讲授新课 (一) 公理4 问题1:平面中直线的平行传递性? 问题2: 利用教室内实例寻找空间中直线平行的传递性. 公理4:平行于同一直线的两条直线相互平行. 公理分析:要证明空间两条直线平行,要找到中间桥梁. (二) 等角定理 问题1:初中学习的等角定理?如果两条相交直线与另两条相交直线分别平行,那么这两组相交直线所成角相等或互补. 问题2:在空间中,这个定理仍然成立吗? 等角定理(书第9页):如果两条相交直线与另两条相交直线分别平行,那么这两组相交直线所成的锐角(或直角)相等. 注意表述上区别:平面几何合立体几何中某些理论上的不一致应引起学生掌握理论时的重视. 证明:书第9页 (三)例题分析 例1:在长方体中,E、F分别为,AD 的中点,求证 : 证明:取BC中点G,连结 B [例题解析]:学会在空间中借助平行四边形,寻找起到桥梁作用的直线. A A B B D C B E F 例2 书例1 (见书第9页) [说明]公理4应用于作图题中. 例3 在长方体中, 求证:. A B B D C B A B 证明:, , 是锐角,. [说明]:掌握在空间中利用直线的平行来证明角相等. (四)、问题拓展 1、空间四边形 空间四边形相关知识复习:在空间四边形ABCD中,E、H分别为AB、AD中点,F、G为CB、CD三等分点,且.求证:EF,HG,AC 三线共点. [说明]复习公理1、2 ,对于空间四边形——这一立体几何内的新事物,进行回顾和整理,为下一步更好学习做好准备. 例4 已知E、F、G、H分别是空间四边形ABCD各边中点. (1) 判断四边形EFGH 形状;(答:平行四边形.通过公理4) (2) 若空间四边形中对角线AC=BD,判断四边形EFGH 形状;(答:菱形.平行四边形对角线相互垂直) (3) 四边形EFGH什么情况下为矩形?(答:对角线相互垂直,即) (4) 结合(2)、(3),可得正方形EFGH (5) 第(2)、(3)、(4)题的逆命题是否成立?该如何求证? 如(2) 若四边形EFGH中,,则AC=BD (6) 若E、H分别为AB、AD中点,F、G为CB、CD三等分点,且,判断四边形EFGH 形状.(梯形EFGH) 证明:E、H分别为AB、AD中点 梯形EFGH [说明] 这是空间两条直线平行——公理4的典型应用,加以推测、证明的重要应用. 2、对于平面图形的结论: 有些可推广到立几图形并有完全相同的结论; 有些在立几图形中有相似的结论,但不完全相同; 有些在立几中则有完全不同的结论. 三、巩固练习 练习14.2(1);1、2 四、课堂小结 1.空间两条直线平行的判定. 2.空间中等角定理得由来与应用 3.空间四边形各边中点的相关问题 4. 平面几何与立体几何结论间的比较与联系 五、课后作业 练习册相关习题 补充作业: 1. 在正方体中,点E、F分别是 中点,判断四边形的形状并加以证明. 2.正方体中,E、F 分别为AB、BC 中点,试画出过点E、F、的截面. A A A A D F C E B A 3.在正方体中,点E、F 分别在AB、AD 上,点G,H分别在 上,且满足,联结 求证: 4.空间四边形ABCD的各边中点依次为E、F、G、H,连结EG、FH. (1)求证:EG 与HF 互相平分 (2)若BD=2,AC=4,求的值. A 5.如图:在空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,若AC+BD=m,AC+BD=n,则= B C D 6.如图,A是ΔBCD所在平面外一点,M,N分别是ΔABC和ΔACD的重心,若BD=6,求MN的长. A B C D M N E F 六、教学设计说明 1、对教材的研究认识: 空间中直线与直线的平行关系,并非本章节内容的难点和重点.但是由于平面几何中也有平行的传递性质和等角定理,因此,对于学生数学类比、推测、论证能力都是一格很好的锻炼机会.因此除去基本知识要点以外,在教学设计上,我还有意识地加强类比、推测、论证能力的培养.此外,在空间几何的常规图形中,除了长方体、正方体等几何体外,空间四边形也有非常重要的地位.在立体几何刚刚开始的平面内容中,空间四边形——这一典型图形就频频出现,对于同学在三维空间中掌握知识要点十分有帮助.因此,探究空间四边形相关内容和知识要点,对于同学学习和掌握立体几何相关内容非常有帮助.所以在内容教授上又添加了空间四边形中线段平行理论的研究. 2、 课堂教学模式的设置: 自主探究是传统教学模式的一种补充,自主探究能够使学生成为研究问题的主人,能够培养学生的思维能力.数学是思维的科学,思维能力是数学的核心,教学过程的设计要能够体现教学本质;能够突出所学数学内容的本质;组织教学的过程要能触及学生的灵魂深处.因此,课堂教学中提倡问题教学,抓住学生的认识现实,恰当地创设问题情境,使学习者能够在课堂上进行积极有效的学习. 3、 课堂练习题的说明: 由于通过类比的教学方式,学生对于公理4和等角定理得学习未必能引起足够的重视.由于从平面中推广到空间中仍然成立.所以对于大多数同学来讲,一定觉得比较简单.可是对于空间想象能力比较差的同学来讲,在空间中未必能非常好的掌握利用平行证明角度相等.可能仍旧会应用平面几何中的知识来证明,因此空间能力的掌握目标并没有达到.因此老师在教授时也要注意空间想象能力的引导和对于此类题目的重视.空间四边形内容的扩充题也在锻炼同学应用和计算、分析等能力.查看更多