- 2021-04-17 发布 |
- 37.5 KB |
- 22页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教数学八年级上册全册学案
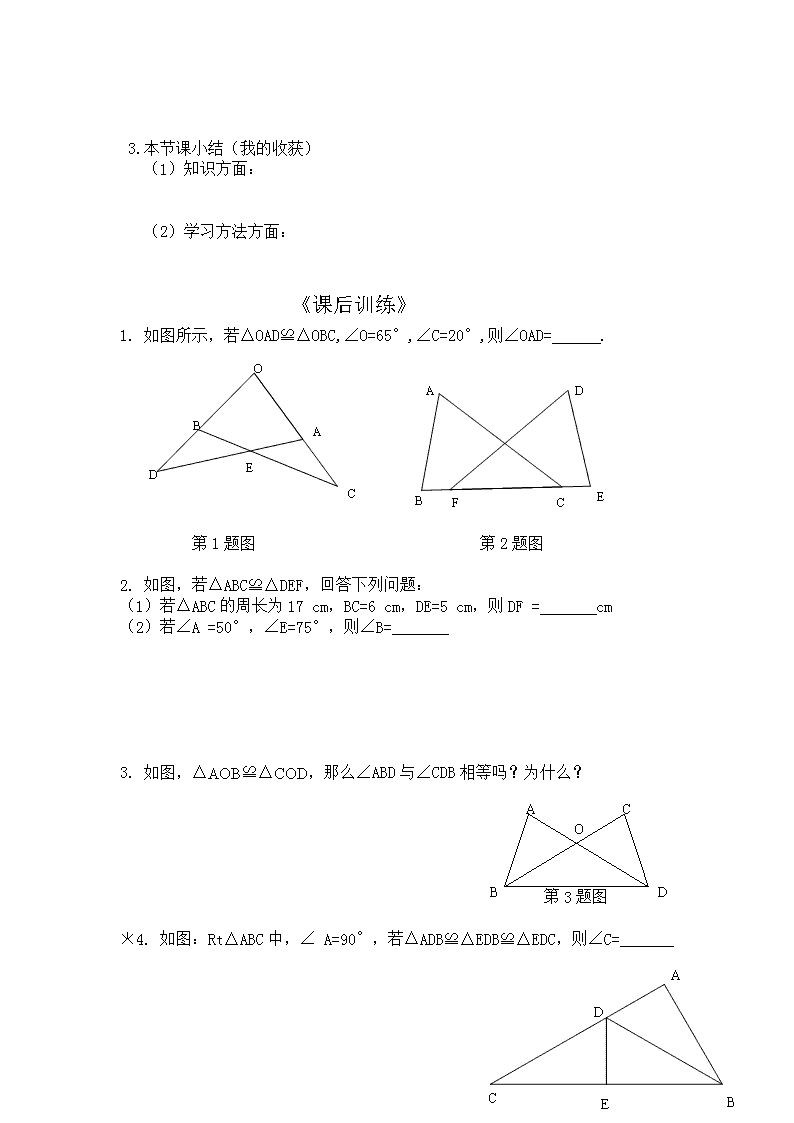
第十一章:全等三角形导学案 黑龙江省依兰县第一中学 朱庆伟 11.1《全等三角形》导学案 【使用说明与学法指导】 1. 课前完成预习案,牢记基础知识,掌握基本题型,时间不超过15分钟。 2 .组内探究、合作学习完成《课内探究》不超过20分钟。 3.小组长在课上合作探究环节要在组内起引领示范作用,控制讨论节奏。 4.人人参与,合作学习,人人都有收获,人人都有进步。 5.带﹡的题要多动脑筋,展示你的能力。 一、学习目标: 1.理解全等三角形的概念,能识别全等三角形的对应顶点、对应边、对应角。 2.掌握全等三角形的性质,并运用性质解决有关的问题。 3.会用符号表示全等三角形及他们的对应元素,培养大家的符号意识。 二、重点难点:运用全等三角形的性质解决相关的计算及证明等问题。 三、学习过程 《课前预习案》 (一)、自主预习课本2—3页内容,回答下列问题: 1、能够______________的图形就是全等图形, 两个全等图形的_________和________完全相同。 2、一个图形经过______、______、_________后所得的图形与原图形 。 3、把两个全等的三角形重合在一起,重合的顶点叫做 ,重合的边叫做 ,重合的角叫做 。“全等”用“ ”表示,读作 。 4、如图所示,△OCA≌△OBD, 对应顶点有:点___和点___,点___和点___,点___和点___; 对应角有:____和____,_____和_____,_____和_____; 对应边有:____和____,____和____,_____和_____. 5、全等三角形的性质:全等三角形的 相等, 相等。 (二)、练一练 1.如图,△ABC≌△CDA,AB和CD,BC和DA是对应边。写出其他对应边及对应角。 2如图,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边。写出其他对应边及对应角。 (三)、我的疑惑 《课内探究》 1.如图△EFG≌△NMH,∠F和∠M是对应角.在△EFG中,FG是最长边. 在△NMH中,MH是最长边.EF=2.1㎝,EH=1.1㎝,HN=3.3㎝. (1)写出其他对应边及对应角. (2)求线段MN及线段HG的长. 2.如图,△ABC≌△DEC,CA和CD,CB和CE是对应边.∠ACD和∠BCE相等吗? 为什么? 3.本节课小结(我的收获) (1)知识方面: (2)学习方法方面: 《课后训练》 1. 如图所示,若△OAD≌△OBC,∠O=65°,∠C=20°,则∠OAD= . 第1题图 第2题图 2. 如图,若△ABC≌△DEF,回答下列问题: (1)若△ABC的周长为17 cm,BC=6 cm,DE=5 cm,则DF = cm (2)若∠A =50°,∠E=75°,则∠B= 3. 如图,△AOB≌△COD,那么∠ABD与∠CDB相等吗?为什么? B D O A C 第3题图 ﹡4. 如图:Rt△ABC中,∠ A=90°,若△ADB≌△EDB≌△EDC,则∠C= 课题:《11.2三角形全等的判定》(SSS)导学案 【使用说明与学法指导】: 1.学生利用自习先预习课本第6、7页完成《课前预习案》(15分钟)。 2 .组内探究、合作学习完成《课内探究》(20分钟) 3.小组长在课上合作探究环节要在组内起引领示范作用,控制讨论节奏。 4. 积极投入,激情展示,做最佳自己。 5.带﹡的题要多动脑筋,展示你的能力。 【学习目标】 1、能自己试验探索出判定三角形全等的SSS判定定理。 2 、会应用判定定理SSS进行简单的推理判定两个三角形全等 3、会作一个角等于已知角. 【学习重点】:三角形全等的条件. 【学习难点】:寻求三角形全等的条件. 【学习过程】: 《课前预习案》 一、自主学习 1、复习:什么是全等三角形?全等三角形有些什么性质? 如图,△ABC≌△DCB那么 相等的边是: 相等的角是: 2、讨论三角形全等的条件(动手画一画并回答下列问题) (1).只给一个条件:一组对应边相等(或一组对应角相等),画出的两个三角形一定全等吗? (2).给出两个条件画三角形,有____种情形。按下面给出的两个条件,画出的两个三角形一定全等吗? ①一组对应边相等和一组对应角相等 ②两组对应边相等 ③两组对应角相等 (3)、给出三个条件画三角形,有____种情形。按下面给出三个条件,画出的两个三角形一定全等吗? ①三组对应角相等 ②三组对应边相等 已知一个三角形的三条边长分别为6cm、8cm、10cm .你能画出这个三角形吗?把你画的三角形剪下与同伴画的三角形进行比较,它们全等吗? a.作图方法: b.以小组为单位,把剪下的三角形重叠在一起,发现 ,这说明这些三角形都是 的. c.归纳:三边对应相等的两个三角形 ,简写为“ ”或“ ”. d、用数学语言表述: 在△ABC和中, ∵ ∴△ABC≌ ( ) 用上面的规律可以判断两个三角形 . “SSS”是证明三角形全等的一个依据. 《课内探究》 二、合作探究 1、[例]如图,△ABC是一个钢架,AB=AC,AD是连结点A与BC中点D的支架. 求证:△ABD≌△ACD. 证明:∵D是BC ∴ = ∴在△ 和△ 中 AB= BD= AD= ∴△ABD △ACD( ) 温馨提示:证明的书写步骤: ①准备条件:证全等时需要用的间接条件要先证好; ②三角形全等书写三步骤: A、写出在哪两个三角形中,B、摆出三个条件用大括号括起来,C、写出全等结论。 2、如图,OA=OB,AC=BC. 求证:∠AOC=∠BOC. 3、尺规作图。 已知:∠AOB. 求作:∠DEF,使∠DEF=∠AOB 4.本节课小结(我的收获) (1)知识方面: (2)学习方法方面: 三、课堂巩固练习. 1、如图,AB=AE,AC=AD,BD=CE,求证:△ABC ≌ ADE。 2、已知:如图,AD=BC,AC=BD. 求证:∠OCD=∠ODC 《课后训练》 1、下列说法中,错误的有( )个 (1)周长相等的两个三角形全等。(2)周长相等的两个等边三角形全等。(3)有三个角对应相等的两个三角形全等。(4)有三边对应相等的两个三角形全等 A、1 B、2 C、3 D、4 2.如图,点B、E、C、F在同一直线上,且AB=DE,AC=DF,BE=CF,请将下面说明ΔABC≌ΔDEF的过程和理由补充完整。 解:∵BE=CF (_____________) ∴BE+EC=CF+EC 即BC=EF 在ΔABC和ΔDEF中 AB=________ (________________) __________=DF(_______________) BC=__________ ∴ΔABC≌ΔDEF (_____________) 3.如图,已知AB=DE,BC=EF,AF=DC,则∠EFD=∠BCA,请说明理由。 ﹡4.如图,在△ABC中,AB=AC,D是BC的中点,点E在AD上,找出图中全等的三角形,并说明它们为什么是全等的. 课题:《11.2三角形全等的判定》(SAS)导学案 【使用说明与学法指导】: 1.学生课前预习课本第9页完成(自主学习1、4) 2 .组内探究、合作学习完成(探究一、探究二) 3.小组长在课上合作探究环节要在组内起引领示范作用,控制讨论节奏。 4. 积极投入,激情展示,做最佳自己。 5.带﹡的题要多动脑筋,展示你的能力。 【学习目标】 1、掌握三角形全等的“SAS”条件,能运用“SAS”证明简单的三角形全等问题 2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程. 3、积极投入,激情展示,做最佳自己。 教学重点:SAS的探究和运用. 教学难点:领会两边及其中一边的对角对应相等的两个三角形不一定全等. 【学习过程】 一、自主学习 1、复习思考 (1)怎样的两个三角形是全等三角形?全等三角形的性质是什么?三角形全等的判定(一)的内容是什么? (2)上节课我们知道满足三个条件画两个三角形有4种情形,三个角对应相等;三条边对应相等;两角和一边对应相等;两边和一角对应相等;前两种情况已经研究了,今天我们来研究第三种两边和一角的情况,这种情况又要分两边和它们的夹角,两边及其一边的对角两种情况。 2、探究一:两边和它们的夹角对应相等的两个三角形是否全等? (1)动手试一试 已知:△ABC 求作:,使,, (2) 把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合? (3)归纳;由上面的画图和实验可以得出全等三角形判定(二): 两边和它们的夹角对应相等的两个三角形 (可以简写成“ ”或“ ”) (4)用数学语言表述全等三角形判定(二) 在△ABC和中, ∵ ∴△ABC≌ 3、探究二:两边及其一边的对角对应相等的两个三角形是否全等? 通过画图或实验可以得出: 4.例题学习 (再次温馨提示:证明的书写步骤: ①准备条件:证全等时需要用的间接条件要先证好; ②三角形全等书写三步骤: A、写出在哪两个三角形中,B、摆出三个条件用大括号括起来,C、写出全等结论。) 5.我的疑惑: 二、学以致用 三、当堂检测 1、 如图,AD⊥BC,D为BC的中点,那么结论正确的有 A、△ABD≌△ACD B、∠B=∠C C、AD平分∠BAC D、△ABC是等边三角形 2、如图,已知OA=OB,应填什么条件就得到△AOC≌△BOD (允许添加一个条件) 3、 ﹡四、能力提升:(学有余力的同学完成) 如图,已知CA=CB,AD=BD,M、N分别是CA、CB的中点,求证:DM=DN 五、课堂小结 1、两边和它们的夹角对应相等的两个三角形全等。简写成“ ”或“ ” 2、到目前为止,我们一共探索出判定三角形全等的2种方法,它们分别是: 和 六、作业:第15页习题11.2 3-4 第16页第10题 课题:《11.2三角形全等的判定》(ASA、AAS)导学案 使用说明:学生利用自习先预习课本第11页-12页10分钟,然后35分钟独立做完学案。正课由小组讨论交流10分钟,25分钟展示点评,10分钟整理落实,对于有疑问的题目教师点拨、拓展。 【学习目标】 1、掌握三角形全等的“角边角”“角角边”条件.能运用全等三角形的条件,解决简单的推理证明问题 2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程. 3、积极投入,激情展示,体验成功的快乐。 教学重点:已知两角一边的三角形全等探究. 教学难点:灵活运用三角形全等条件证明. 【学习过程】 一、自主学习 1、复习思考 (1).到目前为止,可以作为判别两三角形全等的方法有几种?各是什么? (2).在三角形中,已知三个元素的四种情况中,我们研究了三种,今天我们接着探究已知两角一边是否可以判断两三角形全等呢?三角形中已知两角一边又分成哪两种呢? 2、探究一:两角和它们的夹边对应相等的两个三角形是否全等? (1)动手试一试。 已知:△ABC 求作:△,使=∠B, =∠C,=BC,(不写作法,保留作图痕迹) (2) 把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合? (3)归纳;由上面的画图和实验可以得出全等三角形判定(三): 两角和它们的夹边对应相等的两个三角形 (可以简写成“ ”或“ ”) (4)用数学语言表述全等三角形判定(三) 在△ABC和中, ∵ ∴△ABC≌ 3、探究二。两角和其中一角的对边对应相等的两三角形是否全等 (1)如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF,△ABC与△DEF全等吗?能利用前面学过的判定方法来证明你的结论吗? (2)归纳;由上面的证明可以得出全等三角形判定(四): 两个角和其中一角的对边对应相等的两个三角形 (可以简写成“ ”或“ ”) (3)用数学语言表述全等三角形判定(四) 在△ABC和中, ∵ ∴△ABC≌ 二、合作探究 1、例1、如下图,D在AB上,E在AC上,AB=AC,∠B=∠C. 求证:AD=AE. 2.已知:点D在AB上,点E在AC上, BE⊥AC, CD⊥AB,AB=AC,求证:BD=CE 三、学以致用 3、如图,在△ABC中,∠B=2∠C,AD是△ABC的角平分线,∠1=∠C,求证AC=AB+CE 四、课堂小结 (1)今天我们又学习了两个判定三角形全等的方法是: (2)三角形全等的判定方法共有 五、课后检测 1、 2、 3、 4.满足下列哪种条件时,就能判定△ABC≌△DEF ( ) A. AB=DE,BC=EF, ∠A=∠E; B. AB=DE,BC=EF, ∠C=∠F C. ∠A=∠E,AB=EF, ∠B=∠D; D. ∠A=∠D,AB=DE, ∠B=∠E A F C D 1 2 E B 5.如图所示,已知∠A=∠D,∠1=∠2,那么要 得到△ABC≌△DEF,还应给出的条件是:( ) A. ∠B=∠E B.ED=BC C. AB=EF D.AF=CD 6.如6题图, 在△ABC和△DEF中,AF=DC, ∠A=∠D, 当_____________时,可根据“ASA”证明△ABC≌△DEF 课题:《11.2三角形全等的判定》(HL)导学案 使用说明:学生利用自习先预习课本第13、14页10分钟,然后35分钟独立做完学案。正课由小组讨论交流10分钟,25分钟展示点评,10分钟整理落实,对于有疑问的题目教师点拨、拓展。 【学习目标】 1、理解直角三角形全等的判定方法“HL”,并能灵活选择方法判定三角形全等; 2.通过独立思考、小组合作、展示质疑,体会探索数学结论的过程,发展合情推理能力; 3. 极度热情、高度责任、自动自发、享受成功。 教学重点:运用直角三角形全等的条件解决一些实际问题。 教学难点:熟练运用直角三角形全等的条件解决一些实际问题。 【学习过程】 一、自主学习 1、复习思考 (1)、判定两个三角形全等的方法: 、 、 、 (2)、如图,Rt△ABC中,直角边是 、 ,斜边是 (3)、如图,AB⊥BE于B,DE⊥BE于E, ①若∠A=∠D,AB=DE, 则△ABC与△DEF (填“全等”或“不全等” ) 根据 (用简写法) ②若∠A=∠D,BC=EF, 则△ABC与△DEF (填“全等”或“不全等” ) 根据 (用简写法) ③若AB=DE,BC=EF, 则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法) ④若AB=DE,BC=EF,AC=DF 则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法) 2、如果两个直角三角形满足斜边和一条直角边对应相等,这两个直角三角形全等吗? (1)动手试一试。 已知:Rt△ABC 求作:Rt△, 使=90°, =AB, =BC 作法: (2) 把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合? (3)归纳;由上面的画图和实验可以得到判定两个直角三角形全等的一个方法 斜边与一直角边对应相等的两个直角三角形 (可以简写成“ ”或“ ”) A B C A1 B1 C1 (4)用数学语言表述上面的判定方法 在Rt△ABC和Rt中, ∵ ∴Rt△ABC≌Rt△ (5)直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法 “ ”、 “ ”、 “ ”、 “ ”、 还有直角三角形特殊的判定方法 “ ” 二、合作探究 1、如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗? 2、如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系? 三、学以致用 1、如图,△ABC中,AB=AC,AD是高, 则△ADB与△ADC (填“全等”或“不全等” ) 根据 (用简写法) 2、判断两个直角三角形全等的方法不正确的有( ) A、两条直角边对应相等 B、斜边和一锐角对应相等 C、斜边和一条直角边对应相等 D、两个锐角对应相等 3、如图,B、E、F、C在同一直线上,AF⊥BC于F,DE⊥BC于E, AB=DC,BE=CF,你认为AB平行于CD吗?说说你的理由 答:AB平行于CD 理由:∵ AF⊥BC,DE⊥BC (已知) ∴ ∠AFB=∠DEC= °(垂直的定义) ∵BE=CF,∴BF=CE 在Rt△ 和Rt△ 中 ∵∴ ≌ ( ) ∴ = ( ) ∴ (内错角相等,两直线平行) 四、能力提升:(学有余力的同学完成) 如图1,E、F分别为线段AC上的两个动点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点。(1)求证:MB=MD,ME=MF;(2)当E、F两点移动至图2所示的位置时,其余条件不变,上述结论是否成立?若成立,给予证明。 五、当堂检测 如图,CE⊥AB,DF⊥AB,垂足分别为E、F, (1)若AC//DB,且AC=DB,则△ACE≌△BDF,根据 (2)若AC//DB,且AE=BF,则△ACE≌△BDF,根据 (3)若AE=BF,且CE=DF,则△ACE≌△BDF,根据 (4)若AC=BD,AE=BF,CE=DF。则△ACE≌△BDF,根据 (5) 若AC=BD,CE=DF(或AE=BF),则△ACE≌△BDF,根据 六、课堂小结 这节课你有什么收获呢?与你的同伴进行交流 作业:第16页习题11.2 7-8 第17页第13题 课题:《11.3角的平分线的性质》(1)导学案 使用说明:学生利用自习先预习课本第19页探究-第21页思考前10分钟,然后35分钟独立做完学案。正课由小组讨论交流10分钟,25分钟展示点评,10分钟整理落实,对于有疑问的题目教师点拨、拓展。 【学习目标】 1、经历角的平分线性质的发现过程,初步掌握角的平分线的性质定理. 2、能运用角的平分线性质定理解决简单的几何问题. 3、极度热情、高度责任、自动自发、享受成功。 教学重点:掌握角的平分线的性质定理 教学难点: 角平分线定理的应用。 【学习过程】 一、自主学习 1、复习思考 什么是角的平分线?怎样画一个角的平分线? 2.如右图,AB=AD,BC=DC, 沿着A、C画一条射线AE,AE就是∠BAD的角平分线,你知道为什么吗 3.根据角平分仪的制作原理,如何用尺规作角的平分线?自学课本19页后,思考为什么要用大于MN的长为半径画弧? 4.OC是∠AOB的平分线,点P是射线OC上的任意一点, 操作测量:取点P的三个不同的位置,分别过点P作PD⊥OA,PE ⊥OB,点D、E为垂足,测量PD、PE的长.将三次数据填入下表:观察测量结果,猜想线段PD与PE的大小关系,写出结论 PD PE 第一次 第二次 第三次 5、命题:角平分线上的点到这个角的两边距离相等. 题设:一个点在一个角的平分线上 结论:这个点到这个角的两边的距离相等 结合第4题图形请你写出已知和求证,并证明命题的正确性 解后思考:证明一个几何命题的步骤有那些? 6、用数学语言来表述角的平分线的性质定理: 如右上图,∵OC是∠AOB的平分线,点P是 ∴ 二、合作探究 1、如图所示OC是∠AOB 的平分线,P 是OC上任意一点,问PE=PD?为什么? O A B E D C P 2、如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF; 求证:CF=EB 三、学以致用 E D C B A 在Rt△ABC中,BD平分∠ABC, DE⊥AB于E,则 ⑴图中相等的线段有哪些?相等的角呢? ⑵哪条线段与DE相等?为什么? ⑶若AB=10,BC=8,AC=6,求BE,AE的长和△AED的周长。 四、当堂检测 如图,在△ABC中,AC⊥BC,AD为∠BAC的平分线,DE⊥AB,AB=7㎝,AC=3㎝,求BE的E D C B A 长 五、课堂小结 这节课你有什么收获呢?与你的同伴进行交流 六、作业: 第22页习题11.3 1-2 第23页第4-5题 课题:《11.3角的平分线的性质》(2)导学案 使用说明:学生利用自习先预习课本第21页8分钟,然后30分钟独立做完学案。正课由小组讨论交流10分钟,25分钟展示点评,10分钟整理落实,对于有疑问的题目教师点拨、拓展。 【学习目标】 1、会叙述角的平分线的性质及“到角两边距离相等的点在角的平分线上”. 2、能应用这两个性质解决一些简单的实际问题. 3、极度热情、高度责任、自动自发、享受成功。 教学重点:角平分线的性质及其应用 教学难点: 灵活应用两个性质解决问题。 【学习过程】 一、自主学习 1、复习思考 (1)、画出三角形三个内角的平分线 你发现了什么特点吗? (2)、如图,△ABC的角平分线BM,CN相交于点P,求证:点P到三边AB,BC,CA的距离相等。 2、求证:到角的两边的距离相等的点在角的平分线上。 (提示:先画图,并写出已知、求证,再加以证明) 3、要在S区建一个集贸市场,使它到公路,铁路 距离相等且离公路,铁路的交叉处500米,应建在何处?(比例尺 1:20 000) 二、合作探究 1、比较角平分线的性质与判定 2、如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,OB=OC,求证∠1=∠2 三、学以致用 22页练习题 四、能力提高(*) 如图,在四边形ABCD中,BC>BA,AD=DC,BD平分∠ABC,求证:∠A+∠C=180° 五、课堂小结 这节课你有什么收获呢?与你的同伴进行交流 六、作业 1、已知△ABC中,∠A=60°,∠ABC,∠ACB的平分线交于点O,则∠BOC的度数为 2、下列说法错误的是( ) A、到已知角两边距离相等的点都在同一条直线上 B、一条直线上有一点到已知角的两边的距离相等,则这条直线平分已知角 C、到已知角两边距离相等的点与角的顶点的连线平分已知角 D、已知角内有两点各自到两边的距离相等,经过这两点的直线平分已知角 3、到三角形三条边的距离相等的点是( ) A、三条中线的交点 B、三条高线的交点 C、三条边的垂直平分线的交点 D、三条角平分线的交点 4、课本23页第6题 课题:第十一章全等三角形复习(1、2) 一、学习目标: 1.知道第十一章全等三角形知识结构图. 2.通过基本训练,巩固第十一章所学的基本内容. 3.通过典型例题的学习和综合运用,加深理解第十一章所学的基本内容,发展能力. 二、学习重点和难点: 1.重点:知识结构图和基本训练. 2.难点:典型例题和综合运用. 三、归纳总结,完善认知 1.总结本章知识点及相互联系. 两两边一____ 两边一对角 ____________ ____________ 三边______________ ___边_____________ 两角一边对应相等 __________________ 一个条件 两个条件 三个条件 2.三角形全等 探究 三角形 全等的 条件 四、基本训练,掌握双基 1.填空 (1)能够 的两个图形叫做全等形,能够 的两个三角形叫做全等三角形. (2)把两个全等的三角形重合到一起,重合的顶点叫做 ,重合的边叫做 ,重合的角叫做 . (3)全等三角形的 边相等,全等三角形的 角相等. (4) 对应相等的两个三角形全等(边边边或 ). (5)两边和它们的 对应相等的两个三角形全等(边角边或 ). (6)两角和它们的 对应相等的两个三角形全等(角边角或 ). (7)两角和其中一角的 对应相等的两个三角形全等(角角边或 ). (8) 和一条 对应相等的两个直角三角形全等(斜边、直角边或 ). (9)角的 上的点到角的两边的距离相等. 2.如图,图中有两对三角形全等,填空: (1)△CDO≌ ,其中,CD的对应边是 , DO的对应边是 ,OC的对应边是 ; (2)△ABC≌ ,∠A的对应角是 , ∠B的对应角是 ,∠ACB的对应角是 . 3.判断对错:对的画“√”,错的画“×”. (1)一边一角对应相等的两个三角形不一定全等. ( ) (2)三角对应相等的两个三角形一定全等. ( ) (3)两边一角对应相等的两个三角形一定全等. ( ) (4)两角一边对应相等的两个三角形一定全等. ( ) (5)三边对应相等的两个三角形一定全等. ( ) (6)两直角边对应相等的两个直角三角形一定全等. ( ) (7)斜边和一条直角边对应相等的两个直角三角形不一定全等. ( ) (8)一边一锐角对应相等的两个直角三角形一定全等. ( ) 4.如图,AB⊥AC,DC⊥DB,填空: (1)已知AB=DC,利用 可以判定 △ABO≌△DCO; (2)已知AB=DC,∠BAD=∠CDA,利用 可以判△ABD≌△DCA; (3)已知AC=DB,利用 可以判定△ABC≌△DCB; (4)已知AO=DO,利用 可以判定△ABO≌△DCO; (5)已知AB=DC,BD=CA,利用 可以判定△ABD≌△DCA. 5.完成下面的证明过程: 如图,OA=OC,OB=OD. 求证:AB∥DC. 证明:在△ABO和△CDO中, ∴△ABO≌△CDO( ). ∴∠A= . ∴AB∥DC( 相等,两直线平行). 6.完成下面的证明过程: 如图,AB∥DC,AE⊥BD,CF⊥BD,BF=DE. 求证:△ABE≌△CDF. 证明:∵AB∥DC, ∴∠1= . ∵AE⊥BD,CF⊥BD, ∴∠AEB= . ∵BF=DE, ∴BE= . 在△ABE和△CDF中, ∴△ABE≌△CDF( ). 五、典型题目,加深理解 题1 如图,AB=AD,BC=DC. 求证:∠B=∠D. 题2 证明:角的内部到角的两边的距离相等的点在角的平分线上. (先结合图形理解命题的意思,然后结合图形写出已知和求证,已知、求证及证明过程) 题3 如图,CD⊥AB,BE⊥AC,OB=OC. 求证:∠1=∠2. 六、综合运用,发展能力 7.如图,OA⊥AC,OB⊥BC,填空: (1)利用“角的平分线上的点到角的两边 的距离相等”,已知 = , 可得 = ; (2)利用“角的内部到角两边距离相等的点在角的平分线上”, 已知 = ,可得 = ; 8.如图,要在S区建一个集贸市场, 使它到公路、铁路的距离相等,并且离公 路与铁路交叉处300米.如果图中1 厘米表示100米,请在图中标出集 贸市场的位置. 9.如图,CD=CA,∠1=∠2,EC=BC. 求证:DE=AB. 10.如图,AB=DE,AC=DF,BE=CF. 求证:AB∥DE. 11.如图,在△ABC中,D是BC的中点, DE⊥AB,DF⊥AC,BE=CF. 求证:AD是△ABC的角平分线. (第11题图) 12.选做题: 如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE. 求证:△ACD≌△CBE. (第12题图)查看更多