- 2021-04-17 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019届中考数学一轮复习 第9课时 平面直角坐标系教案
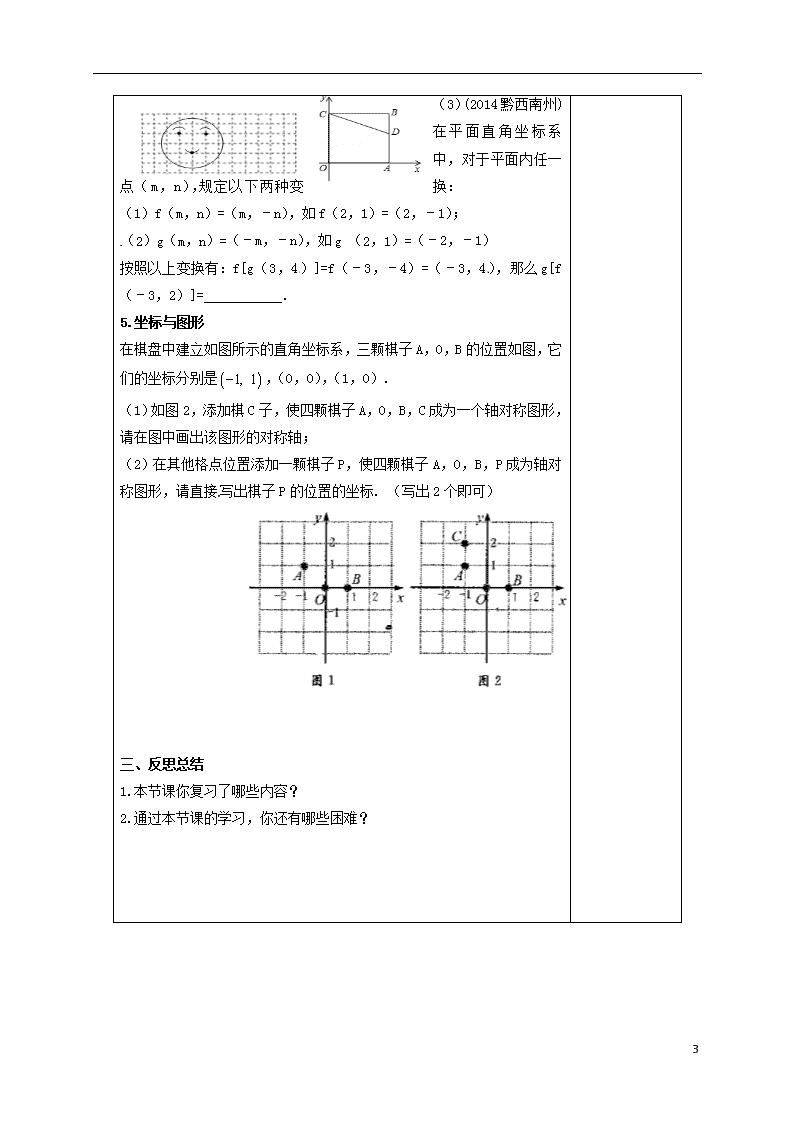
平面直角坐标系 课 题 §9平面直角坐标系 复备人 教学时间 教学目标: 1.理解直角坐标系的有关概念,会根据坐标确定点的位置和由点的位置确定坐标,并能够在方格纸上建立适当的直角坐标系描述物体的位置; 2.能够在同一直角坐标系内感受图形变换前后点的坐标的变化规律,灵活运用不同的方式确定物体的位置。 教学重点: 直角坐标系中的点与坐标的对应关系。 教学难点: 直角坐标系中的点与坐标的对应关系。 教学方法: 自主探究 合作交流 讲练结合 教学媒体: 电子白板 【教学过程】: 一.知识梳理 1.有序实数对 平面内的点和有序实数对是 的关系,即平面内的任何一个点可以用一对 来表示;反过来每一对有序实数都表示平面内的一个点. 2.平面内点的坐标规律 (1)各象限内点的坐标的特征 点P(x,y)在第一象限 则 ; 点P(x,y)在第二象限 则 点P(x,y)在第三象限 则 ; 点P(x,y)在第四象限 则 (2)坐标轴上的点的坐标的特征 点P(x,y)在x轴上,则 ,x为任意实数; 点P(x,y)在y轴上,则 ,y为任意实数; 点P(x,y)在坐标原点,则 3.平行于坐标轴的直线上的点的坐标特征 (1)平行于x轴(或垂直于y轴)的直线上点的 相同,横坐标为不相等的实数. (2)平行于y轴(或垂直于x轴)的直线上点的 相同,纵坐标为不相等的实数. 2.各象限角平分线上的点的坐标特征 (1) 若点P(x,y)为一、三象限角平分线上的点,则 . (2) 若点P(x,y为第二、四象限角平分线上的点,则 . 3.对称点的坐标特征 (1)点P(x,y)关于x轴的对称点P1的坐标为 . 复 备 栏 3 (2)关于y轴的对称点P2的坐标为 . (3)关于原点的对称点P3的坐标为 . 4.坐标与距离 (1))点P(x,y)到x轴的距离为 .到y轴的距离为 . 到原点的距离为 . (2)若,则线段AB的中点P的坐标为 ,线段AB的长度为 二、典型例题 1.对称点的特征 已知点P(3,-4),填写下列空格: 点P关于x轴对称的点的坐标为 ;点P关于轴对称的点的坐标为 ; 点P关于原点对称的点的坐标为 ;关于点对称的点的坐标为 ; 2.坐标与距离 点P到轴的距离为 ;点P到轴的距离为 ; 点P到原点的距离为 ;点P到的距离为 ; 3.象限内点的坐标特征 (1)若点M(,)满足=,则点M所在象限是第 象限. (2)若a为任意实数,点一定不再第( )象限 A.一 B. 二 C. 三 D.四 4.图形变换与坐标 (1)如图,把“QQ”笑脸放在直角坐标系中,已知左眼A的坐标是(-2,3),嘴唇C点的坐标为(-1,1),则将此“QQ”笑脸向右平移3个单位后,右眼B的坐标是 . (2)如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 3 (3)(2014黔西南州)在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换: (1)f(m,n)=(m,﹣n),如f(2,1)=(2,﹣1); (2)g(m,n)=(﹣m,﹣n),如g (2,1)=(﹣2,﹣1) 按照以上变换有:f[g(3,4)]=f(﹣3,﹣4)=(﹣3,4),那么g[f(﹣3,2)]= . 5.坐标与图形 在棋盘中建立如图所示的直角坐标系,三颗棋子A,O,B的位置如图,它们的坐标分别是,(0,0),(1,0). (1)如图2,添加棋C子,使四颗棋子A,O,B,C成为一个轴对称图形,请在图中画出该图形的对称轴; (2)在其他格点位置添加一颗棋子P,使四颗棋子A,O,B,P成为轴对称图形,请直接写出棋子P的位置的坐标. (写出2个即可) 三、反思总结 1.本节课你复习了哪些内容? 2.通过本节课的学习,你还有哪些困难? 3查看更多