五年级上册数学教案-5平行四边形的面积 ▏沪教版 (2)

五年级上册数学教案-5平行四边形的面积 ▏沪教版 (2)

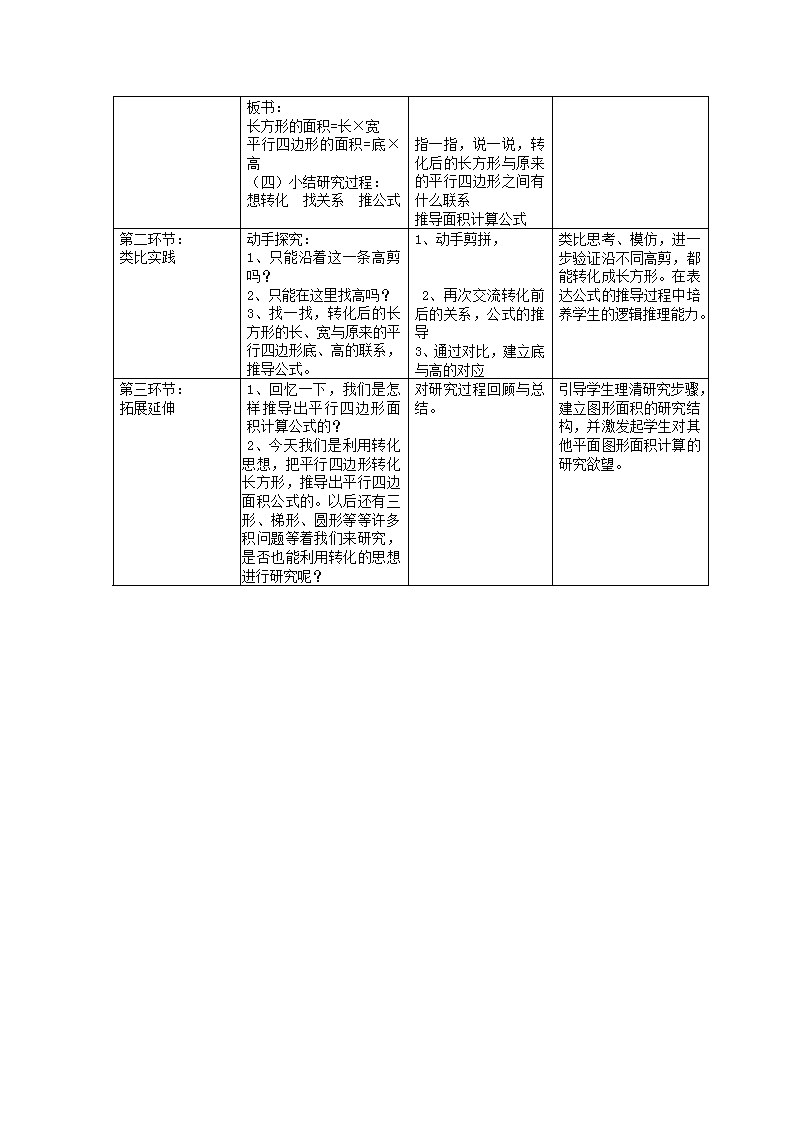
教学设计方案 学科：数学 课题：平行四边形面积 日期：‎ 1、 教学目标 （1） 通过动手操作，将平行四边形转化为长方形，体验的转化思想，了解转化这一方法在平面图形计算中的运用。‎ （2） 探索转化后长方形与原来平行四边形之间的联系，推导出平行四边形面积计算公式，经历平行四边形的面积计算公式的形成过程。‎ 2、 目标制定的依据：‎ 教材分析：‎ 本节课平行四边形面积虽然不是平面图形面积计算学习的起始内容，但却是学生首次运用转化思想，通过两者之间的联系，推导出新图形的面积计算公式。本节课的教学是后续学习中，学生能主动运用平行四边形面积计算的探究结构来推导三角形、梯形、圆等平面图形面积计算公式的基础。本节课不仅要引导学生理解掌握平面图形面积计算公式，更要学会转化，学会推导，让学生感受转化方法在图形面积计算中的作用，为后续进一步探究活动提供基本思路，提高自主探究推导平面图形面积计算公式的能力。‎ 学生分析：‎ 学生在三年级时，已通过方格纸数出了叶子、规则图形、不规则图形的面积，大量感知的面积概念，并从长方形面积的探究中，抽象概括出长方形、正方形面积计算公式。学生在四年级计算组合图形面积与周长时，初步有了一些的转化的思想，已经知道了推、拉后，组合图形的周长不变，但面积变了，可以用分割、平移、翻转，改变形状通过转化求组合图形面积。在本单元学习中，学生认识了平行四边形的特征和特性，认识了底和高，会画平行四边形底边上对应的高。在本课中，学生可能在转化时凭直觉，转化成长方形，但不能体悟到转化背后的道理。在寻找图形转化前后两者之间的联系，推导公式过程时，语言表达存在一些困难。‎ 教 学 过 程 教学环节 教师活动 学生活动 设计意图 常规积累 这些图形你都认识吗？你能计算哪些图形的面积？‎ 独立思考 集体交流 回顾长正方形长方形面积计算方法，为学生的探究提供支撑。‎ 核心过程推进 第一环节：‎ 初步转化 （一） 动手探究：‎ ‎1、今天我们就来研究平行四边形面积。‎ ‎1、平行四边形可以转化成我们学过的什么图形，就可以计算它的面积了？‎ ‎（二）辨析 ‎1、这些转化都成功吗？‎ ‎2、为什么沿着平行四边形的高剪，就一定能将平行四边形转化成长方形？‎ ‎（三）联系 ‎1、转化后的长方形与原来的平行四边形之间有什么联系？）‎ 归纳公式 动手剪拼转化 预设：‎ ‎1、面积变小 ‎2、没有沿高剪 ‎3、沿着高剪拼 回应策略：‎ 辨析、讨论 这些转化都成功吗？‎ ‎ ‎ 为什么沿着平行四边形的高剪，就一定能将平行四边形转化成长方形？‎ 通过放手让学生尝试将平行四边形转化长方形，初步体会到等积变形的转化思想，并根据两者之间的联系，推导出平行四边形面积计算公式。初步感知了平面图形面积计算公式的研究步骤。‎ 通过追问，发现并验证转化成功的关键——沿高剪。感悟到转化时要抓住两者之间的区别，掌握转化的基本方法。‎ 板书：‎ 长方形的面积=长×宽 平行四边形的面积=底×高 ‎ ‎（四）小结研究过程：‎ 想转化 找关系 推公式 ‎ 指一指，说一说，转化后的长方形与原来的平行四边形之间有什么联系 推导面积计算公式 第二环节：‎ 类比实践 动手探究：‎ ‎1、只能沿着这一条高剪吗？‎ ‎2、只能在这里找高吗？‎ ‎3、找一找，转化后的长方形的长、宽与原来的平行四边形底、高的联系，推导公式。‎ ‎1、动手剪拼，‎ ‎ 2、再次交流转化前后的关系，公式的推导 ‎3、通过对比，建立底与高的对应 类比思考、模仿，进一步验证沿不同高剪，都能转化成长方形。在表达公式的推导过程中培养学生的逻辑推理能力。‎ 第三环节：‎ 拓展延伸 ‎1、回忆一下，我们是怎样推导出平行四边形面积计算公式的？‎ ‎2、今天我们是利用转化的思想，把平行四边形转化成长方形，推导出平行四边形面积公式的。以后还有三角形、梯形、圆形等等许多面积问题等着我们来研究，它是否也能利用转化的思想来进行研究呢？‎ 对研究过程回顾与总结。‎ 引导学生理清研究步骤，建立图形面积的研究结构，并激发起学生对其他平面图形面积计算的研究欲望。‎