- 2021-04-17 发布 |
- 37.5 KB |
- 18页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教新课标数学五年级下册 期末测试卷8(附答案)
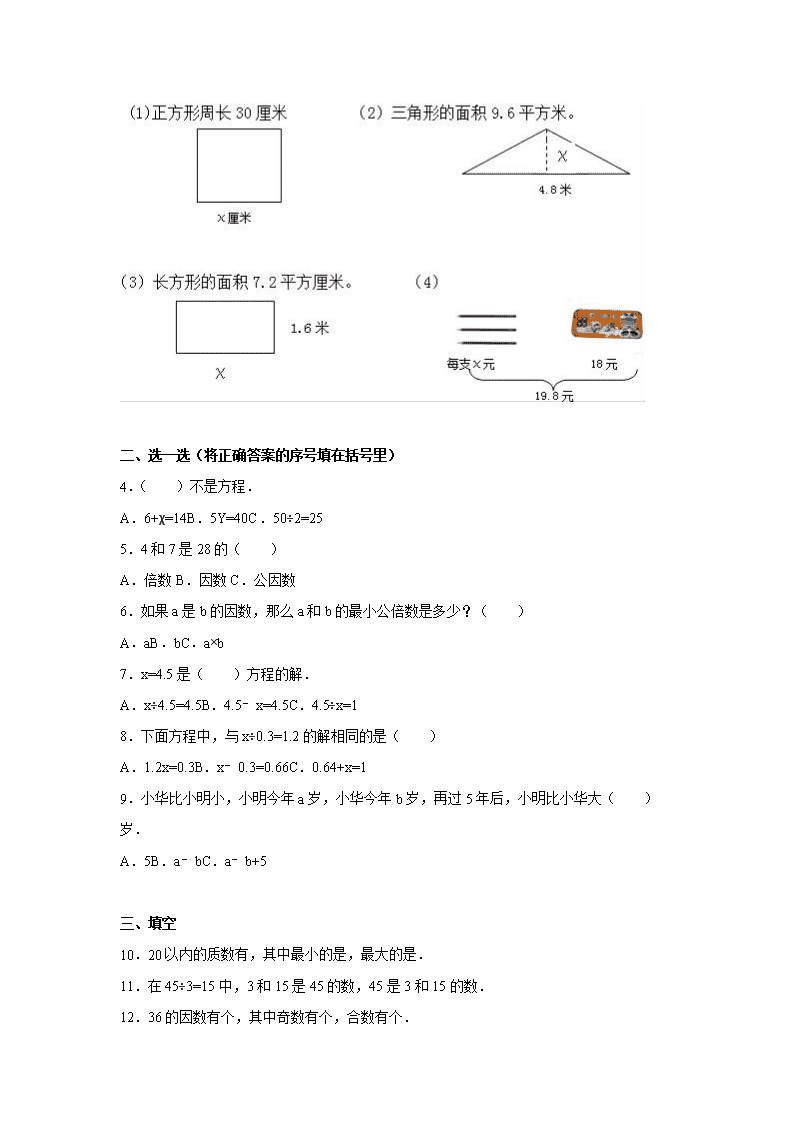
小学五年级(下)调研数学试卷 一、算一算 1.计算下面各组数的最小公倍数和最大公因数. 7和 14 9和 12 35和 14. 2.解方程. 3 5 + x = 4 8 x ÷ 2 . 5 = 5 4 . 8 ﹣ x = 3 . 5 2 x + 1 . 2 = 4 . 6 4 x ﹣ 4 . 8 = 5 . 6 3 x ÷ 5 = 1 2 3.看图列方程并解答 二、选一选(将正确答案的序号填在括号里) 4.( )不是方程. A.6+χ=14B.5Y=40C.50÷2=25 5.4和 7是 28的( ) A.倍数 B.因数 C.公因数 6.如果 a是 b的因数,那么 a和 b的最小公倍数是多少?( ) A.aB.bC.a×b 7.x=4.5是( )方程的解. A.x÷4.5=4.5B.4.5﹣x=4.5C.4.5÷x=1 8.下面方程中,与 x÷0.3=1.2的解相同的是( ) A.1.2x=0.3B.x﹣0.3=0.66C.0.64+x=1 9.小华比小明小,小明今年 a岁,小华今年 b岁,再过 5年后,小明比小华大( )岁. A.5B.a﹣bC.a﹣b+5 三、填空 10.20以内的质数有,其中最小的是,最大的是. 11.在 45÷3=15中,3和 15是 45的数,45是 3和 15的数. 12.36的因数有个,其中奇数有个,合数有个. 13.一个数的最大因数是 24,这个数的最小倍数是. 14.一个三位数,它的百位上是最小的质数,十位上是最小的合数,个位上的数是合数又是 奇数,这个三位数是. 15.在○里填上“>、<或=”. (1)当 X=17时 X+19○36 (2)当 X=2时 2X○6 (3)当 X=38时,45﹣X○8 (4)当 X=1.5时 9÷X○5. 16.三个连续偶数的和是 36,这三偶数是、和. 17.小李有 128个卡片,比小兰的 2倍多 24个,小兰有卡片. 18.将下列数量关系式补充完整. (1)中华人民共和国国旗长应是宽的 1.5倍.一面国旗长 144厘米,宽应是多少厘米? ×1.5﹦. (2)果园里桃树的棵数是梨树的 2.5倍,比梨树多 30棵.桃树和梨树各有多少棵? ﹣﹦30棵. 19.黄花有χ朵,红花的朵数是黄花的 4倍.黄花和红花一共有朵,红花比黄花多朵. 20.下面是一位病人的体温记录折线图: (1)护士每隔小时给病人量一次体温. (2)这位病人的最高体温是摄氏度;最低体温是摄氏度. (3)病人在 5月 6日 18时的体温是摄氏度. (4)从体温看,这位病人的病情是在.(填“好转”或“恶化”) 四、判断题(对的在括号里面画“√”,错的在括号里面画“×”) 21.1.5÷3=0.5 1.5是 3的倍数..(判断对错) 22.两个数的公因数的个数是无限的..(判断对错) 23.两个数的最小公倍数一定比这两个数的最大公因数大..(判断对错) 24.X﹣Y=0 是方程..(判断对错) 25.91除了 1和本身外,没有其它因数..(判断对错) 五、解决问题. 26.将长是 16分米,宽 12分米的长方形分成大小相同的正方形(边长是整分米数),且没 有剩余.至少能分成多少个? 27.五(1)的人数在 40﹣﹣50之间,如果 12人一组能正好分完,如果 8人一组也能正好 分完,这个班有多少人? 28.少先队员采集植物标本和昆虫标本共 60件.植物标本的件数是昆虫标本的 1.5倍,两 种标本各是多少件? 29.甲、乙两辆汽车同时从 A城开往 B城,甲车每小时行 80千米,乙车每小时行 95千米, 几小时后两车相距 60千米? 30.南京长江大桥公路桥长 4589米,比武汉长江大桥公路桥的 3倍少 421米,武汉长江大 桥公路桥长多少米? 江苏省宿迁市泗阳县王集小学五年级(下)调研数学试 卷 参考答案与试题解析 一、算一算 1.计算下面各组数的最小公倍数和最大公因数. 7和 14 9和 12 35和 14. 【考点】求几个数的最大公因数的方法;求几个数的最小公倍数的方法. 【分析】求最大公约数也就是这几个数的公有质因数的连乘积,最小公倍数是共有质因数与 独有质因数的连乘积,由此解决问题即可. 【解答】解:7和 14是倍数关系,最大公约数是 7,最小公倍数是 14; 9=3×3 12=2×2×3 最大公约数是 3,最小公倍数是 3×3×2×2=36; 35=5×7 14=2×7 最大公约数是 7,最小公倍数是 5×2×7=70. 2.解方程. 35+x=48 x÷2.5=5 4.8﹣x=3.5 2x+1.2=4.6 4x﹣4.8=5.6 3x÷5=12 【考点】方程的解和解方程. 【分析】(1)根据等式的性质,两边同减去 35即可; (2)根据等式的性质,两边同乘 2.5即可; (3)根据等式的性质,两边同加上 x,得 3.5+x=4.8,两边再同减去 3.5即可; (4)根据等式的性质,两边同减去 1.2,再同除以 2即可; (5)根据等式的性质,两边同加上 4.8,再同除以 4即可; (6)根据等式的性质,两边同乘 5,再同除以 3即可. 【解答】解:(1)35+x=48 35+x﹣35=48﹣35 x=13 (2)x÷2.5=5 x÷2.5×2.5=5×2.5 x=12.5 (3)4.8﹣x=3.5 4.8﹣x+x=3.5+x 3.5+x=4.8 3.5+x﹣3.5=4.8﹣3.5 x=1.3 (4)2x+1.2=4.6 2x+1.2﹣1.2=4.6﹣1.2 2x=3.4 2x÷2=3.4÷2 x=1.7 (5)4x﹣4.8=5.6 4x﹣4.8+4.8=5.6+4.8 4x=10.4 4x÷4=10.4÷4 x=2.6 (6)3x÷5=12 3x÷5×5=12×5 3x=60 3x÷3=60÷3 x=20 3.看图列方程并解答 【考点】列方程解应用题(两步需要逆思考). 【分析】(1)根据等量关系:正方形的边长×2=周长,列方程解答即可得解; (2)根据三角形的面积公式:三角形的面积=底×高× ,列方程解答即可; (3)根据长方形的面积公式:长方形的面积=长×宽,列方程解答即可; (4)由图形可得等量关系:每支铅笔的价格×铅笔的支数+文具盒的价格=19.8元,列方程 解答即可. 【解答】解:(1)设正方形的边长为 x厘米, 4x=30 4x÷4=30÷4 x=7.5, 答:正方形的边长为 7.5厘米. (2)设三角形的高为 x米, ×4.8x=9.6 2.4x=9.6 2.4x÷2.4=9.6÷2.4 x=4, 答:三角形的高为 4米. (3)设长方形的长为 x米, 1.6x=7.2 1.6x÷1.6=7.2÷1.6 x=4.5, 答:长方形的长为 4.5米. (4)设铅笔每支 x元, 3x+18=19.8 3x=1.8 3x÷3=1.8÷3 x=0.6, 答:铅笔每支 0.6元. 二、选一选(将正确答案的序号填在括号里) 4.( )不是方程. A.6+χ=14B.5Y=40C.50÷2=25 【考点】方程需要满足的条件. 【分析】方程是指含有未知数的等式.所以方程必须具备两个条件:①含有未知数;②等 式.由此进行选择. 【解答】解:A、6+χ=14,既含有未知数又是等式,具备了方程的条件,因此是方程; B、5Y=40,既含有未知数又是等式,具备了方程的条件,因此是方程; C、50÷2=25,只是等式,不含有未知数,不是方程; 故选:C. 5.4和 7是 28的( ) A.倍数 B.因数 C.公因数 【考点】因数和倍数的意义. 【分析】根据因数和倍数的意义:如果数 a能被数 b整除(b≠0),a就叫做 b的倍数,b就 叫做 a的因数;进行解答即可. 【解答】解:因为 28÷7=4,所以 28是 7和 4的倍数,7和 4是 28的因数; 故选:B. 6.如果 a是 b的因数,那么 a和 b的最小公倍数是多少?( ) A.aB.bC.a×b 【考点】求几个数的最小公倍数的方法. 【分析】求两数的最小公倍数,要看两个数之间的关系:两个数互质,则最小公倍数是这两 个数的乘积;两个数为倍数关系,则最小公倍数为较大的数;两个数有公约数的,最小公倍 数是两个数公有质因数与独有质因数的连乘积;由此选择情况解决问题. 【解答】解:因为 a是 b的因数 所以 b是 a的倍数,属于倍数关系,b>a 所以 a和 b最小公倍数是 b. 故选:B. 7.x=4.5是( )方程的解. A.x÷4.5=4.5B.4.5﹣x=4.5C.4.5÷x=1 【考点】方程的解和解方程. 【分析】把 x=4.5分别代入方程,看左右两边是否相等即可. 【解答】解:A、当 x=4.5时,左边=4.5÷4.5=1≠右边 4.5,本项错误; B、当 x=4.5时,左边=4.5﹣4.5=0≠右边 4.5,本项错误; C、当 x=4.5时,左边=4.5÷4.5=1=右边 1,本项正确, 故选:C. 8.下面方程中,与 x÷0.3=1.2的解相同的是( ) A.1.2x=0.3B.x﹣0.3=0.66C.0.64+x=1 【考点】方程的解和解方程. 【分析】要想知道方程 x÷0.3=1.2的解与下面哪个方程的解相同,应先求出方程 x÷0.3=1.2 的解,再把方程的解分别代入下面各方程,看看左边是否等于右边,据此解答. 【解答】解:x÷0.3=1.2 x÷0.3×0.3=1.2×0.3 x=0.36, 把 x=0.36代入 1.2x=0.3中,左边=1.2×0.36=0.432≠右边 0.3,因此 x=0.36不是 x÷0.3=1.2的 解; 把 x=0.36代入 x﹣0.3=0.66中,左边=0.36﹣0.3=0.06≠右边 0.66,因此 x=0.36不是 x﹣0.3=0.66 的解; 把 x=0.36代入 0.64+x=1中,左边=0.64+0.36=1=右边 1,因此 x=0.36是 0.64+x=1的解; 故选:C. 9.小华比小明小,小明今年 a岁,小华今年 b岁,再过 5年后,小明比小华大( )岁. A.5B.a﹣bC.a﹣b+5 【考点】用字母表示数. 【分析】根据“小华比小明小,小明今年 a岁,小华今年 b岁”,说明他们的岁数相差(a﹣b) 岁,因为再过 5年后,他们都增长了相同的岁数,所以他们岁数的差不变,由此即可做出选 择. 【解答】解:因为再过 5年后,小明和小华都增长了相同的岁数. 所以小明比小华大(a﹣b)岁. 故选:B. 三、填空 10.20以内的质数有 2、3、5、7、11、13、17、19 ,其中最小的是 2 ,最大的是 19 . 【考点】合数与质数. 【分析】在自然数中,除了 1和它本身外,没有别的因数的数为质数,据此分析填空即可 【解答】解:20以内的质数有 2、3、5、7、11、13、17、19,其中最小的是 2,最大的是 19; 故答案为:2、3、5、7、11、13、17、19,2,19. 11.在 45÷3=15中,3和 15是 45的 因 数,45是 3和 15的 倍 数. 【考点】因数和倍数的意义. 【分析】根据倍数和因数的意义:如果数 a能被数 b整除(b≠0),a就叫做 b的倍数,b就 叫做 a的因数;据此判断即可. 【解答】解:在 45÷3=15中,3和 15是 45的因数,45是 3和 15的倍数. 故答案为:因,倍. 12.36的因数有 9 个,其中奇数有 3 个,合数有 6 个. 【考点】找一个数的因数的方法;奇数与偶数的初步认识;合数与质数. 【分析】先找出 36的因数,然后根据奇数和合数的定义,在自然数中,不是 2的倍数的数 为奇数;除了 1和它本身外,还有别的因数的数为合数,据此解答即可. 【解答】解:36的因数有 1、2、3、4、6、9、12、18、36共 9个, 其中奇数有 1、3、9共 3个,合数有 4、6、9、12、18、36共 6个. 故答案为:9,3,6. 13.一个数的最大因数是 24,这个数的最小倍数是 24 . 【考点】找一个数的因数的方法;找一个数的倍数的方法. 【分析】根据“一个数最大的因数是它本身,最小的倍数是它本身”可知:这个数是 24,这 个数的最小倍数是 24;由此解答即可. 【解答】解:因为一个数最最大的因数是它本身,所以得出这个数是 24;又因为一个数的 最小倍数是它本身,所以得出这个数的最小倍数是 24; 故答案为:24. 14.一个三位数,它的百位上是最小的质数,十位上是最小的合数,个位上的数是合数又是 奇数,这个三位数是 249 . 【考点】合数与质数;奇数与偶数的初步认识. 【分析】最小的质数是 2,即百位上是 2,最小的合数是 4,即十位上是 4,个位上的数是合 数且是奇数,即个位上是 9,据此写出这个三位数. 【解答】解:这个三位数是:249. 故答案为:249. 15.在○里填上“>、<或=”. (1)当 X=17时 X+19○36 (2)当 X=2时 2X○6 (3)当 X=38时,45﹣X○8 (4)当 X=1.5时 9÷X○5. 【考点】含字母式子的求值. 【分析】把 x表示的数代入含字母的式子中计算,即可求出式子的数值,然后再比较. 【解答】解:(1)当 X=17时, X+19=17+19 =36 所以当 X=17时,X+19=36; (2)当 X=2时, 2X=2×2 =4 4<6,所以当 X=2时,2X<6; (3)当 X=38时, 45﹣X=45﹣38 =7 7<8,所以当 X=38时,45﹣X<8; (4)当 X=1.5时 9÷X=9÷1.5 =6 6>5,所以当 X=1.5时,9÷X>5. 故答案为:=,<,<,>. 16.三个连续偶数的和是 36,这三偶数是 10 、 12 和 14 . 【考点】奇数与偶数的初步认识. 【分析】相邻的偶数相差 2,应该先根据“三个连续偶数的和是 36”这个条件,算出这三个偶 数的平均数,即中间的偶数,前面的偶数比中间的数少 2,后面的偶数是中间的偶数加 2, 据出解答. 【解答】解:36÷3=12, 12﹣2=10, 12+2=14, 答:这三个连续偶数是 10、12、14. 故答案为:10、12、14. 17.小李有 128个卡片,比小兰的 2倍多 24个,小兰有 52张 卡片. 【考点】整数的除法及应用. 【分析】根据题意知,如果小李的卡片数减去 24,则是小兰卡片数的 2倍,再根据已知一 个数的几倍是多少,求这个数用除法,据此解答即可. 【解答】解:÷2 =104÷2 =52(张) 答:小兰有 52张卡片. 故答案为:52张. 18.将下列数量关系式补充完整. (1)中华人民共和国国旗长应是宽的 1.5倍.一面国旗长 144厘米,宽应是多少厘米? 宽 ×1.5﹦ 长 . (2)果园里桃树的棵数是梨树的 2.5倍,比梨树多 30棵.桃树和梨树各有多少棵? 桃树的棵数 ﹣ 梨树的棵数 ﹦30棵. 【考点】整数、小数复合应用题. 【分析】(1)设国旗的宽是 x厘米,根据求一个数几倍是多少,用乘法求计算,根据宽×1.5= 长列方程解答即可. (2)根据题干,设梨树有 x棵,则桃树就是 2.5x棵,根据等量关系:桃树的棵数﹣梨树的 棵数=30棵,据此列出方程解决问题. 【解答】解:(1)宽×1.5=长 设宽是 x厘米. 1.5x=144 x=144÷1.5, x=96 答:宽应该是 96厘米. (2)桃树的棵数﹣梨树的棵数=30棵. 解:设梨树有 x棵,则桃树有 2.5x棵 2.5x﹣x=30 1.5x=30 x=20 20×2.5=50(棵) 答:桃树有 50棵,梨树有 20棵. 故答案为:(1)宽;长;(2)桃树的棵数;梨树的棵数. 19.黄花有χ朵,红花的朵数是黄花的 4倍.黄花和红花一共有 5χ 朵,红花比黄花多 3χ 朵. 【考点】用字母表示数. 【分析】要求红花的朵数,也就是求黄花χ朵的 4倍是多少,用乘法计算,再用红花的朵数 加上黄花的朵数,就是黄花和红花一共的朵有;再用红花的朵数减去黄花的朵数,就是红花 比黄花多的朵数. 【解答】解:χ×4=4χ(朵) 4χ+χ=5χ(朵) 4χ﹣χ=3χ(朵) 答:黄花和红花一共有 5χ朵,红花比黄花多 3χ朵. 故答案为:5χ,3χ. 20.下面是一位病人的体温记录折线图: (1)护士每隔 6 小时给病人量一次体温. (2)这位病人的最高体温是 39.5 摄氏度;最低体温是 36.8 摄氏度. (3)病人在 5月 6日 18时的体温是 39 摄氏度. (4)从体温看,这位病人的病情是在 好转 .(填“好转”或“恶化”) 【考点】单式折线统计图. 【分析】(1)由折线统计图可以看出:护士每隔 12﹣6=6小时给病人量一次体温; (2)折线图中最高的点表示温度最高,最低的点表示温度最低,由此即可求出答案; (3)从折线统计图可以看出:他在 5月 6日 18时的体温是 39摄氏度; (4)曲线呈现下降的趋势,这个病人的病情好转了. 【解答】解::(1)由折线统计图可以看出:护士每隔 12﹣6=6小时给病人量一次体温; (2)这个病人的最高体温是 39.5摄氏度,最低体温是 36.8摄氏度; (3)他在 5月 6日 18时的体温是 39摄氏度; (4)从体温看,这位病人的病情是在好转. 故答案为:(1)6;(2)39.5,36.8;(3)39;(4)好转. 四、判断题(对的在括号里面画“√”,错的在括号里面画“×”) 21.1.5÷3=0.5 1.5是 3的倍数. × .(判断对错) 【考点】因数和倍数的意义. 【分析】根据因数和倍数的意义,当 a÷b=c(a、b、c为非 0自然数)我们说 a是 b的倍数, b是 a的因数.此题 1.5÷3=0.5,0.5是小数,由此可知此题不正确. 【解答】解:因为 1.5÷3=0.5,所以 1.5是 3的倍数,说法错误; 故答案为:×. 22.两个数的公因数的个数是无限的. 错误 .(判断对错) 【考点】因数、公因数和最大公因数. 【分析】两个数的公因数是这两个数公有的因数,因为一个数的因数是有限的,其中最小的 是 1,最大是它本身,那么两个数的公因数的个数也是有限的,据此分析判断. 【解答】解:因为一个数的因数是有限的,其中最小的是 1,最大是它本身,那么两个数的 公因数的个数是有限的,所以两个数的公因数的个数是无限的说法是错误的; 故答案为:错误. 23.两个数的最小公倍数一定比这两个数的最大公因数大. × .(判断对错) 【考点】求几个数的最大公因数的方法;求几个数的最小公倍数的方法. 【分析】求最大公因数也就是这几个数的公有质因数的连乘积,最小公倍数是公有质因数与 独有质因数的连乘积;所以两个不同的数的最小公倍数一定比这两个数的最大公因数大,但 如果两个数相同 例如:4和 4的最小公倍数和最大公因数都相同. 【解答】解:因为求最大公因数也就是这几个数的公有质因数的连乘积,最小公倍数是公有 质因数与独有质因数的连乘积; 所以两个数的最小公倍数一定比这两个数的最大公因数大,但如果两个数相同 例如:4和 4 的最小公倍数和最大公因数都相同. 故判断:×. 24.X﹣Y=0 是方程. √ .(判断对错) 【考点】方程的解和解方程. 【分析】含有未知数的等式是方程,据此即可判断. 【解答】解:X﹣Y=0,是含有未知数的等式,所以是方程; 故答案为:√. 25.91除了 1和本身外,没有其它因数. × .(判断对错) 【考点】找一个数的因数的方法. 【分析】把 91分解质因数,91=7×13,所以 91除了 1和它本身,还有其他的因数 7、13; 由此解答即可. 【解答】解:91除了 1和它本身,还有其他的因数 7、13. 所以 91除了 1和本身外,没有其它因数说法错误. 故答案为:×. 五、解决问题. 26.将长是 16分米,宽 12分米的长方形分成大小相同的正方形(边长是整分米数),且没 有剩余.至少能分成多少个? 【考点】公因数和公倍数应用题. 【分析】根据题意,要想没有剩余,至少可以截多少个正方形,也就是使正方形的边长是长 和宽的最大公因数,然后用长方形的面积除以每个正方形的面积. 【解答】解:16=2×2×2×2, 12=2×2×3, 所以 16和 12的最大公因数是:2×2=4, 16×12÷(4×4) =192÷16 =12(个); 答:至少能分成 12个. 27.五(1)的人数在 40﹣﹣50之间,如果 12人一组能正好分完,如果 8人一组也能正好 分完,这个班有多少人? 【考点】公因数和公倍数应用题. 【分析】根据公倍数的意义,两个或者几个数公有的倍数叫做这两个或者这几个数的公倍 数.因为一个数的倍数的个数是无限的,所以两个数的公倍数的个数也是无限的;先求出 8 和 12的公倍数,再根据这个班小数人数在 30﹣﹣50人之间来确定这个班的学生人数. 【解答】解:先求 8和 12的最小公倍数,把 8和 12分别分解质因数,它们的公有质因数和 独有质因数的连乘积就是它们的最小公倍数; 8=2×2×2, 12=2×2×3, 8和 12的最小公倍数是:2×2×2×3=24; 8和 12的公倍数有:24,48,72…; 其中在 40和 50之间的是 48,所以这个班有 48人. 答:这个班有 48名学生. 28.少先队员采集植物标本和昆虫标本共 60件.植物标本的件数是昆虫标本的 1.5倍,两 种标本各是多少件? 【考点】和倍问题. 【分析】根据题意,植物标本的件数是昆虫标本的 1.5倍,那么采集植物标本和昆虫标本共 60件就是昆虫标本的 1.5+1=2.5倍,用除法即可得昆虫标本的件数,再求植物标本即可. 【解答】解:60÷(1.5+1) =60÷2.5 =24(件) 60﹣24=36(件) 答:采集植物标本 36件,昆虫标本 24件. 29.甲、乙两辆汽车同时从 A城开往 B城,甲车每小时行 80千米,乙车每小时行 95千米, 几小时后两车相距 60千米? 【考点】简单的行程问题. 【分析】首先用乙车的速度减去甲车的速度,求出两车的速度之差是多少;然后根据路程÷ 速度=时间,用 60除以两车的速度之差,求出几小时后两车相距 60千米即可. 【解答】解:60÷(95﹣80) =60÷15 =4(小时) 答:4小时后两车相距 60千米. 30.南京长江大桥公路桥长 4589米,比武汉长江大桥公路桥的 3倍少 421米,武汉长江大 桥公路桥长多少米? 【考点】整数的除法及应用. 【分析】由题意可知:武汉长江大桥公路桥×3﹣421=南京长江大桥的公路桥长,据此代入 数据即可求解. 【解答】解:设武汉长江大桥的公路桥长 y米,根据题意得: 3y﹣421=4589 3y=5010 y=1670 答:武汉长江大桥的公路桥长 1670米.查看更多