2019-2020学年山东省济南市章丘区八年级(下)期末数学试卷
2019-2020学年山东省济南市章丘区八年级(下)期末数学试卷
一.选择题(本大题共12小题,每小题4分,共48分.在每个小题给出四个选项中只有一项符合题目要求)
1. 若a>b,则下列各式中一定成立的是( )
A.a−2
b2 D.−2a>−2b
2. 在下列因式分解的过程中,分解因式正确的是( )
A.x2−4=(x+4)(x−4) B.x2+2x+4=(x+2)2
C.x2−4x+4=(x−2)2 D.x2+4=(x+2)2
3. 垃圾分类功在当代利在千秋,下列垃圾分类指引标志图形中,是轴对称图形又是中心对称图形的是( )
A.可回收物Recyclable
B.厨余垃圾FoodWaste
C.其他垃圾ResidualWaste
D.有害垃圾HazardousWaste
4. 若式子x−1x−2在实数范围内有意义,则x的取值范围是( )
A.x≤1 B.x≥1且x≠2 C.x>1且x≠2 D.x<1
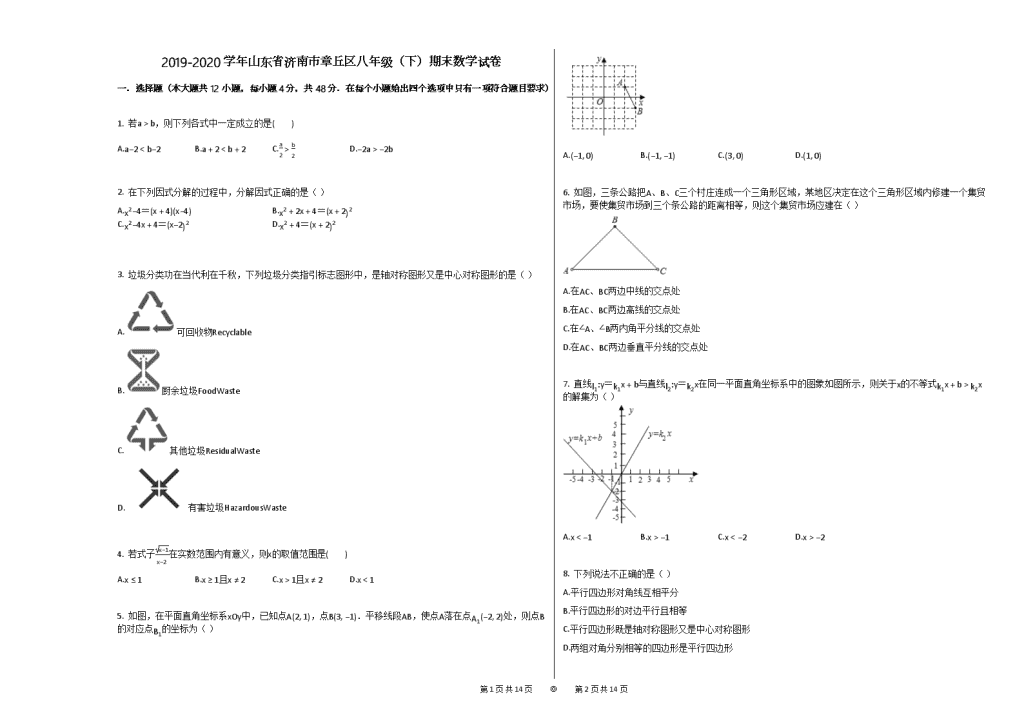
5. 如图,在平面直角坐标系xOy中,已知点A(2, 1),点B(3, −1).平移线段AB,使点A落在点A1(−2, 2)处,则点B的对应点B1的坐标为( )
A.(−1, 0) B.(−1, −1) C.(3, 0) D.(1, 0)
6. 如图,三条公路把A、B、C三个村庄连成一个三角形区域,某地区决定在这个三角形区域内修建一个集贸市场,要使集贸市场到三个条公路的距离相等,则这个集贸市场应建在( )
A.在AC、BC两边中线的交点处
B.在AC、BC两边高线的交点处
C.在∠A、∠B两内角平分线的交点处
D.在AC、BC两边垂直平分线的交点处
7. 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b>k2x的解集为( )
A.x<−1 B.x>−1 C.x<−2 D.x>−2
8. 下列说法不正确的是( )
A.平行四边形对角线互相平分
B.平行四边形的对边平行且相等
C.平行四边形既是轴对称图形又是中心对称图形
D.两组对角分别相等的四边形是平行四边形
第13页 共14页 ◎ 第14页 共14页
9. 若不等式2x+53−1≤2−x的解集中x的每一个值,都能使关于x的不等式2x+m<1成立,则m的取值范围是( )
A.m≤−35 B.m<−35 C.m>−35 D.m≥−35
10. 如图,将△ABC绕点A逆时针旋转90∘得到相应的△ADE,若点D恰在线段BC的延长线上,则下列选项中错误的是( )
A.∠ACB=120∘ B.∠BAD=∠CAE
C.∠CDE=90∘ D.∠ABC=45∘
11. 如图,在△ABC中,∠ABC=90∘,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )
A.8 B.7 C.9 D.10
12. 已知x+1x=6,则x2+1x2=( )
A.36 B.38 C.32 D.34
二.填空题(本大题共6小题,每小题4分,共24分)
分解因式:3ax2−12a=________.
关于x的方程3x+a=1的解是非负数,则a的取值范围是________.
若一个多边形的内角和与外角和之和是900∘,则该多边形的边数是________.
当m=________时,解分式方程x−5x−3=m3−x会出现增根.
我们把三角形中最大内角与最小内角的度数差称为该三角形的“内角正度值”.如果等腰三角形的“内角正度值”为45∘,那么该等腰三角形的顶角等于________.
如图,在▱ABCD,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:①∠BCD=2∠DCF;②EF=CF;③S△CDF=S△CEF;④∠DFE=3∠AEF,一定成立的是________.(把所有正确结论的序号都填在横线上)
三、解答题(本大题共9小题,共78分解答应写出文字说明、证明过程或演算步骤)
解不等式组4(x+1)≤2x+6x−3<x−53 ,并写出它的所有非负整数解.
先化简,再求值:(x+1x−2−1)÷x2−2xx2−4x+4,其中x=3.
如图,平行四边形ABCD中,O是对角线BD的中点,过点O作直线EF分别交AD、BC于点E、F,连结BE、DF,求证:四边形BEDF是平行四边形.
如图,在△ABC中,∠ACB=45∘,过点A作AD⊥BC于点D,点E为AD上一点,且ED=BD.
(1)求证:△ABD≅△CED;
第13页 共14页 ◎ 第14页 共14页
(2)若CE为∠ACD的角平分线,求∠BAC的度数.
阅读下面的材料:
常用的分解因式的方法有提取公因式法,公式法等,但有的多项式只用上述方法无法分解.如x2−4y2−2x+4y,细心观察这个式子,会发现前两项符合平方差公式,后两项可提取公因式,前、后两部分分别因式分解后又出现新的公因式,提取公因式就可以完成整个式子的分解因式.具体过程如下:
x2−4y2−2x+4y
=(x2−4y2)−(2x−4y)
=(x+2y)(x−2y)−2(x−2y)
=(x−2y)(x+2y−2)
像这种将一个多项式适当分组后,进行分解因式的方法叫做分组分解法.
利用分组分解法解决下面的问题:
(1)分解因式:x2−2xy+y2−4;
(2)已知△ABC的三边长a,b,c满足a2−ab−ac+bc=0,判断△ABC的形状并说明理由.
如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点分别为A(−2, 2),B(0, 5),C(0, 2).
(1)画△A1B1C1,使它与△ABC关于点C成中心对称,则B1的坐标为________;
(2)平移△ABC,使点A的对应点A2的坐标为(−4, −6),画出平移后对应的△A2B2C2,则B2的坐标为________;
(3)若将△A1B1C1绕某一点旋转可得到△A2B2C2,则旋转中心的坐标为________.
复课返校后,为了拉大学生锻炼的间距,某学校决定增购适合独立训练的两种体育器材:跳绳和毽子,已知跳绳的单价比毽子的单价多4元,用1000元购买的跳绳个数和用800元购买的键子数量相同.
(1)求跳绳和毽子的单价分别是多少元?
(2)学校计划购买跳绳和毽子两种器材共400个,由于受疫情影响,商场决定对这两种器材打折销售,其中跳绳以八折出售,毽子以七五折出售,学校要求跳绳的数量不少于毽子数量的3倍,跳绳的数量不多于310根,请你求出学校花钱最少的购买方案.
如图1,在Rt△ABC中,AB=AC,∠A=90∘,点D、E分别在边AB、AC上,AD=AE,连结DC,点M、P、N分别为DE、DC、BC的中点.
(1)观察猜想:
图1中,线段PM与PN的数量关系是________,位置关系是________;
(2)探究证明:
把△ADE绕点A逆时针方向旋转到图2的位置,连结MN,判断△PMN的形状,并说明理由;
(3)拓展延伸:
把△ADE绕点A在平面内自由旋转,若DE=2,BC=4,请直接写出△PMN面积的最大值.
在平面直角坐标系xOy中,已知点A (1, 1),B (3, 2).
(1)如图1,在y轴上是否存在一点P,使PA+PB最小,若存在求出点P的坐标;若不存在,请说明理由.
第13页 共14页 ◎ 第14页 共14页
(2)如图2,点C坐标为(4, 1),点D由原点O沿x轴正方向以每秒1个单位的速度运动,求点D运动几秒时,四边形ABCD是平行四边形;
(3)点P在x轴上,点Q在y轴上,且以A、B、P、Q为顶点的四边形是平行四边形,请直接写出点P以及对应的点Q的坐标.
第13页 共14页 ◎ 第14页 共14页
参考答案与试题解析
2019-2020学年山东省济南市章丘区八年级(下)期末数学试卷
一.选择题(本大题共12小题,每小题4分,共48分.在每个小题给出四个选项中只有一项符合题目要求)
1.
【答案】
此题暂无答案
【考点】
不等都着性质
【解析】
此题暂无解析
【解答】
此题暂无解答
2.
【答案】
此题暂无答案
【考点】
提公明式钾与公牛法的北合运用
【解析】
此题暂无解析
【解答】
此题暂无解答
3.
【答案】
此题暂无答案
【考点】
中心较称图腾
轴正算图形
【解析】
此题暂无解析
【解答】
此题暂无解答
4.
【答案】
此题暂无答案
【考点】
分式根亮义况无意肌的条件
二次根式较意夏的条件
【解析】
此题暂无解析
【解答】
此题暂无解答
5.
【答案】
此题暂无答案
【考点】
坐标与图体变某-平移
【解析】
此题暂无解析
【解答】
此题暂无解答
6.
【答案】
此题暂无答案
【考点】
角平较线的停质
【解析】
此题暂无解析
【解答】
此题暂无解答
7.
【答案】
此题暂无答案
【考点】
一次验我与一萄一次人等式
【解析】
此题暂无解析
【解答】
此题暂无解答
8.
【答案】
此题暂无答案
【考点】
轴正算图形
中心较称图腾
平常四占形符性渐与判定
【解析】
此题暂无解析
【解答】
此题暂无解答
9.
【答案】
此题暂无答案
【考点】
解一元因次不丙式
【解析】
第13页 共14页 ◎ 第14页 共14页
此题暂无解析
【解答】
此题暂无解答
10.
【答案】
此题暂无答案
【考点】
旋因末性质
【解析】
此题暂无解析
【解答】
此题暂无解答
11.
【答案】
此题暂无答案
【考点】
等体三火暗服判定与性质
勾体定展
三角形因位线十理
【解析】
此题暂无解析
【解答】
此题暂无解答
12.
【答案】
此题暂无答案
【考点】
完全明方养式
【解析】
此题暂无解析
【解答】
此题暂无解答
二.填空题(本大题共6小题,每小题4分,共24分)
【答案】
此题暂无答案
【考点】
提公明式钾与公牛法的北合运用
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
解一元因次不丙式
一元一常方陆的解
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
多边形正东与外角
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
分式使以的增根
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
等腰三验库的性质
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
平行四表形型性质
直使三碳形望边扩的中线
全根三烛形做给质与判定
【解析】
此题暂无解析
【解答】
此题暂无解答
三、解答题(本大题共9小题,共78分解答应写出文字说明、证明过程或演算步骤)
【答案】
此题暂无答案
第13页 共14页 ◎ 第14页 共14页
【考点】
解一元表次镜等式组
一元三次实等另组每整数解
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
分式因化简优值
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
平常四占形符性渐与判定
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
全根三烛形做给质与判定
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
因式使钡的应用
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
作图验流似变换
作图三腔转变换
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
分式较程的腾用
一三一臂感等散组的应用
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
几何使碳综合题
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
此题暂无答案
【考点】
四边正形合题
【解析】
此题暂无解析
【解答】
此题暂无解答
第13页 共14页 ◎ 第14页 共14页