- 2021-04-17 发布 |
- 37.5 KB |
- 5页

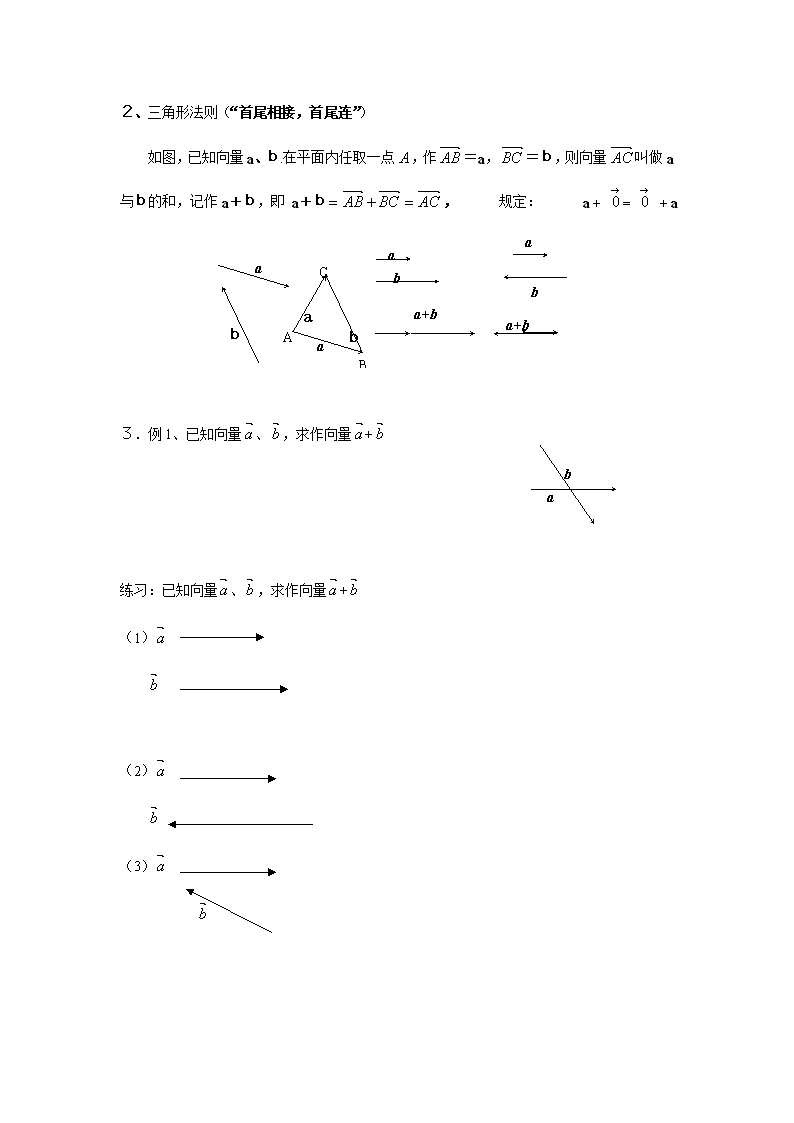

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学必修4教案:2_2_1向量加法运算及其几何意义
2.2.1 向量的加法运算及其几何意义 教学目标: 1、 掌握向量的加法运算,并理解其几何意义; 2、 会用向量加法的三角形法则和平行四边形法则作两个向量的和向量,培养数形结合解决问题的能力; 3、 通过将向量运算与熟悉的数的运算进行类比,使学生掌握向量加法运算的交换律和结合律,并会用它们进行向量计算,渗透类比的数学方法; 教学重点:会用向量加法的三角形法则和平行四边形法则作两个向量的和向量. 教学难点:理解向量加法的定义. 教学思路: 一、设置情景: 1、 复习:向量的定义以及有关概念 强调:向量是既有大小又有方向的量.长度相等、方向相同的向量相等.因此,我们研究的向量是与起点无关的自由向量,即任何向量可以在不改变它的方向和大小的前提下,移到任何位置 2、 情景设置: (1)某人从A到B,再从B按原方向到C, 则两次的位移和: (2)若上题改为从A到B,再从B按反方向到C, 则两次的位移和: (3)某车从A到B,再从B改变方向到C, 则两次的位移和: A B C A B C (4)船速为,水速为,则两速度和: A B C C A B 二、探索研究: 1、向量的加法:求两个向量和的运算,叫做向量的加法. 2、三角形法则(“首尾相接,首尾连”) A B C a+b a+b a a b b a b b a+b a 如图,已知向量a、b.在平面内任取一点,作=a,=b,则向量叫做a与b的和,记作a+b,即 a+b, 规定: a + = + a b a 3.例1、已知向量、,求作向量+ 练习:已知向量、,求作向量+ (1) (2) (3) 探究:(1)两向量的和与两个数的和有什么不同? (2)当向量与不共线时, |+|<||+||;什么时候|+|=||+||, 什么时候|+|=||-||, 当向量与不共线时,,,+的方向不同,且|+|<||+||; 当向量与共线时, ① 当与同向时,则+、、同向,且|+|=||+||, ②当与反向时,若||>||,则+的方向与相同,且|+|=||-||; 若||<||,则+的方向与相同,且|+b|=||-||. (3)“向量平移”(自由向量):使前一个向量的终点为后一个向量的起点,可以推广到n个向量连加 4.加法的交换律和平行四边形法则 已知向量、,求作向量+,+ 问题:上题中+的结果与+是否相同? 从而得到:1)向量加法的平行四边形法则(对于两个向量共线不适应) 2)向量加法的交换律:+=+ 5.你能证明:向量加法的结合律:(+) +=+ (+) 吗? 6.由以上证明你能得到什么结论? 多个向量的加法运算可以按照任意的次序、任意的组合来进行. 三、应用举例: 例2、长江两岸之间没有大桥的地方,常常通过轮渡进行运输。现有一艘船从长江南岸A点出发,以5km/h的速度向垂直于对岸的方向行驶,同时江水的速度为向东2km/h (1) 试用向量表示江水速度、船速及船实际航行的速度(保留两个有效数字); (2) 求船实际航行的速度的大小与方向(用与江水速度之间的夹角表示,精确到度)。 变式1、一艘船从A点出发以的速度向垂直于对岸的方向行驶,船的实际航行速度的大小为,求水流的速度. 变式2、一艘船从A点出发以的速度向垂直于对岸的方向行驶,同时河水的流速为,船的实际航行的速度的大小为,方向与水流间的夹角是,求和. 练习:课本第84页1、2、3、4题 四、小结 1、向量加法的几何意义; 2、交换律和结合律; 3、|+| ≤ || + ||,当且仅当方向相同时取等号. 五、课后作业 习题2.2A组第二题查看更多