2020届高考分类汇编04：立体几何平面解析几何(含解析)

2020届高考分类汇编04：立体几何平面解析几何(含解析)

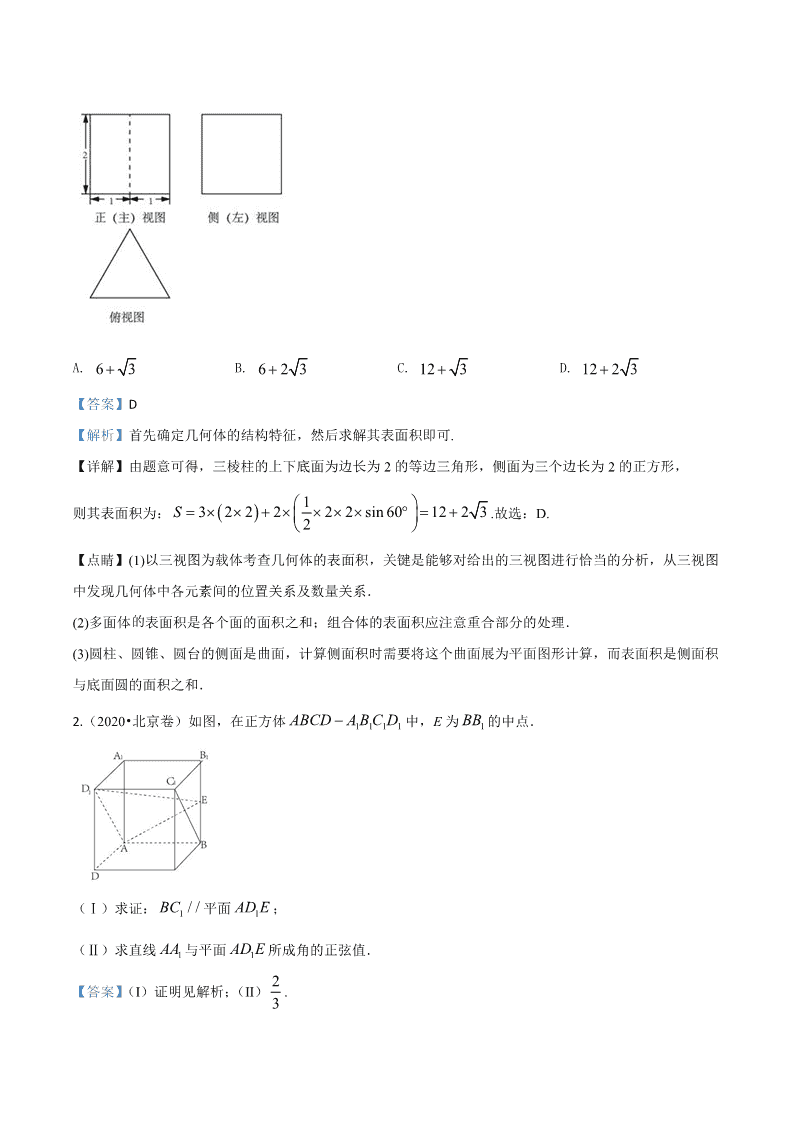
2020 届全国各地高考试题分类汇编目录 01 集合..........................................................................................................................................................................1 02 复数..........................................................................................................................................................................5 03 逻辑用语..................................................................................................................................................................8 04 函数与导数........................................................................................................................................................... 10 05 三角函数和解三角形............................................................................................................................................34 06 平面向量................................................................................................................................................................ 47 07 数列....................................................................................................................................................................... 53 08 不等式和线性规划...............................................................................................................................................69 09 空间立体几何.......................................................................................................................................................73 10 平面解析几何.......................................................................................................................................................98 11 统计和概率.........................................................................................................................................................123 12 极坐标和参数方程.............................................................................................................................................142 13 不等式选讲.........................................................................................................................................................147 09 空间立体几何 1.（2020•北京卷）某三棱柱的底面为正三角形，其三视图如图所示，该三棱柱的表面积为（ ）． 全国高中数学教师群：1142300029 A. 6 3 B. 6 2 3 C. 12 3 D. 12 2 3 【答案】D 【解析】首先确定几何体的结构特征，然后求解其表面积即可. 【详解】由题意可得，三棱柱的上下底面为边长为 2的等边三角形，侧面为三个边长为 2的正方形， 则其表面积为：   13 2 2 2 2 2 sin 60 12 2 3 2 S                .故选：D. 【点睛】(1)以三视图为载体考查几何体的表面积，关键是能够对给出的三视图进行恰当的分析，从三视图 中发现几何体中各元素间的位置关系及数量关系． (2)多面体的表面积是各个面的面积之和；组合体的表面积应注意重合部分的处理． (3)圆柱、圆锥、圆台的侧面是曲面，计算侧面积时需要将这个曲面展为平面图形计算，而表面积是侧面积 与底面圆的面积之和． 2.（2020•北京卷）如图，在正方体 1 1 1 1ABCD ABC D 中，E为 1BB 的中点． （Ⅰ）求证： 1 / /BC 平面 1AD E； （Ⅱ）求直线 1AA 与平面 1AD E所成角的正弦值． 【答案】（Ⅰ）证明见解析；（Ⅱ） 2 3 . 【解析】（Ⅰ）证明出四边形 1 1ABC D 为平行四边形，可得出 1 1//BC AD ，然后利用线面平行的判定定理可证 得结论； （Ⅱ）以点 A为坐标原点， AD、 AB、 1AA 所在直线分别为 x、 y、 z轴建立空间直角坐标系 A xyz ， 利用空间向量法可计算出直线 1AA 与平面 1AD E所成角的正弦值. 【详解】（Ⅰ）如下图所示： 在正方体 1 1 1 1ABCD ABC D 中， 1 1//AB A B 且 1 1AB A B ， 1 1 1 1//AB C D 且 1 1 1 1A B C D ， 1 1//AB C D 且 1 1AB C D ，所以，四边形 1 1ABC D 为平行四边形，则 1 1//BC AD ， 1BC  平面 1AD E， 1AD 平面 1AD E， 1 //BC 平面 1AD E； （Ⅱ）以点 A为坐标原点， AD、 AB、 1AA 所在直线分别为 x、 y、 z轴建立如下图所示的空间直角坐标 系 A xyz ， 设正方体 1 1 1 1ABCD ABC D 的棱长为 2，则  0,0,0A 、  1 0,0, 2A 、  1 2,0,2D 、  0,2,1E ，  1 2,0, 2AD   ，  0,2,1AE   ， 设平面 1AD E的法向量为  , ,n x y z  ，由 1 0 0 n AD n AE         ，得 2 2 0 2 0 x z y z      ， 令 2z   ，则 2x  ， 1y  ，则  2,1, 2n    . 1 1 1 4 2cos , 3 2 3 n AAn AA n AA              . 因此，直线 1AA 与平面 1AD E所成角的正弦值为 2 3 . 【点睛】本题考查线面平行的证明，同时也考查了利用空间向量法计算直线与平面所成角的正弦值，考查 计算能力，属于基础题. 3.（2020•全国 1卷）埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥，以该四棱 锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方 形的边长的比值为（ ） A. 5 1 4  B. 5 1 2  C. 5 1 4  D. 5 1 2  【答案】C 【解析】设 ,CD a PE b  ，利用 2 1 2 PO CD PE  得到关于 ,a b的方程，解方程即可得到答案. 【详解】如图，设 ,CD a PE b  ，则 2 2 2 2 4 aPO PE OE b    ， 由题意 2 1 2 PO ab ，即 2 2 1 4 2 ab ab  ，化简得 24( ) 2 1 0b b a a     ，解得 1 5 4 b a   （负值舍去）. 故选：C. 【点晴】本题主要考查正四棱锥的概念及其有关计算，考查学生的数学计算能力，是一道容易题. 4.（2020•全国 1卷）已知 , ,A B C为球O的球面上的三个点，⊙ 1O 为 ABC 的外接圆，若⊙ 1O 的面积为 4π， 1AB BC AC OO   ，则球O的表面积为（ ） A. 64π B. 48π C. 36π D. 32π 【答案】A 【解析】由已知可得等边 ABC 的外接圆半径，进而求出其边长，得出 1OO 的值，根据球的截面性质，求 出球的半径，即可得出结论. 【详解】设圆 1O 半径为 r，球的半径为 R，依题意，得 2 4 , 2r r    ， ABC 为等边三角形， 由正弦定理可得 2 sin60 2 3AB r   ， 1 2 3OO AB   ，根据球的截面性质 1OO 平面 ABC， 2 2 2 2 1 1 1 1 1, 4OO O A R OA OO O A OO r        ，球O的表面积 24 64S R   . 故选：A 【点睛】 本题考查球的表面积，应用球的截面性质是解题的关键，考查计算求解能力，属于基础题. 5.（2020•全国 1卷）如图，在三棱锥 P–ABC的平面展开图中，AC=1， 3AB AD  ，AB⊥AC，AB⊥AD， ∠CAE=30°，则 cos∠FCB=______________. 【答案】 1 4  【解析】在 ACE△ 中，利用余弦定理可求得CE，可得出CF，利用勾股定理计算出 BC、BD，可得出 BF ， 然后在 BCF 中利用余弦定理可求得 cos FCB 的值. 【详解】 AB AC ， 3AB  ， 1AC  ，由勾股定理得 2 2 2BC AB AC   ， 同理得 6BD  ， 6BF BD   ，在 ACE△ 中， 1AC  ， 3AE AD  ， 30CAE  ， 由余弦定理得 2 2 2 32 cos30 1 3 2 1 3 1 2 CE AC AE AC AE           ， 1CF CE   ， 在 BCF 中， 2BC  ， 6BF  ， 1CF  ， 由余弦定理得 2 2 2 1 4 6 1cos 2 2 1 2 4 CF BC BFFCB CF BC             .故答案为： 1 4  . 【点睛】本题考查利用余弦定理解三角形，考查计算能力，属于中等题. 6.（2020•全国 1卷）如图，D为圆锥的顶点，O是圆锥底面的圆心，AE为底面直径，AE AD ． ABC 是底面的内接正三角形， P为DO上一点， 6 6 PO DO ． （1）证明： PA 平面 PBC； （2）求二面角 B PC E  的余弦值． 【答案】（1）证明见解析；（2） 2 5 5 . 【解析】（1）要证明 PA 平面 PBC，只需证明 PA PB ， PA PC 即可； （2）以 O为坐标原点，OA为 x轴，ON为 y轴建立如图所示的空间直角坐标系，分别算出平面 PCB的法 向量为 n  ，平面PCE的法向量为m  ，利用公式 cos , | || | n mm n n m         计算即可得到答案. 【详解】（1）由题设，知 DAE△ 为等边三角形，设 1AE  ， 则 3 2 DO  ， 1 1 2 2 CO BO AE   ，所以 6 2 6 4 PO DO  ， 2 2 2 26 6, , 4 4 PC PO OC PB PO OB      又 ABC 为等边三角形，则 2 sin60 BA OA ，所以 3 2 BA  ， 2 2 23 4 PA PB AB   ，则 90APB  ，所以 PA PB ， 同理 PA PC ，又 PC PB P ，所以PA 平面 PBC； （2）过 O作ON∥BC交 AB于点 N，因为 PO 平面 ABC，以 O为坐标原点，OA为 x轴，ON为 y轴建 立如图所示的空间直角坐标系， 则 1 2 1 3 1 3( ,0,0), (0,0, ), ( , ,0), ( , ,0) 2 4 4 4 4 4 E P B C    ， 1 3 2( , , ) 4 4 4 PC      ， 1 3 2( , , ) 4 4 4 PB     ， 1 2( ,0, ) 2 4 PE     ， 设平面 PCB的一个法向量为 1 1 1( , , )n x y z  ， 由 0 0 n PC n PB         ，得 1 1 1 1 1 1 3 2 0 3 2 0 x y z x y z          ，令 1 2x  ，得 1 11, 0z y   ， 所以 ( 2,0, 1)n    ，设平面 PCE的一个法向量为 2 2 2( , , )m x y z  由 0 0 m PC m PE         ，得 2 2 2 2 2 3 2 0 2 2 0 x y z x z         ，令 2 1x  ，得 2 2 32, 3 z y   ， 所以 3(1, , 2) 3 m    故 2 2 2 5cos , 5| | | | 103 3 n mm n n m             ， 设二面角 B PC E  的大小为，则 2 5cos 5   . 【点晴】本题主要考查线面垂直的证明以及利用向量求二面角的大小，考查学生空间想象能力，数学运算 能力，是一道容易题. 7.（2020•全国 2卷）如图是一个多面体的三视图，这个多面体某条棱的一个端点在正视图中对应的点为M ， 在俯视图中对应的点为 N ，则该端点在侧视图中对应的点为（ ） A. E B. F C. G D. H 【答案】A 【解析】根据三视图，画出多面体立体图形，即可求得M 点在侧视图中对应的点. 【详解】根据三视图，画出多面体立体图形， 1 4D D 上的点在正视图中都对应点 M,直线 3 4B C 上的点在俯视图中对应的点为 N, ∴在正视图中对应M ,在俯视图中对应N 的点是 4D ,线段 3 4D D ,上的所有点在侧试图中都对应 E ,∴点 4D 在侧视图中对应的点为 E .故选：A 【点睛】本题主要考查了根据三视图判断点的位置，解题关键是掌握三视图的基础知识和根据三视图能还 原立体图形的方法，考查了分析能力和空间想象，属于基础题. 8.（2020•全国 2卷）已知△ABC是面积为 9 3 4 的等边三角形，且其顶点都在球 O的球面上.若球 O的表面 积为 16π，则 O到平面 ABC的距离为（ ） A. 3 B. 3 2 C. 1 D. 3 2 【答案】C 【解析】根据球O的表面积和 ABC 的面积可求得球O的半径R和 ABC 外接圆半径 r，由球的性质可 知所求距离 2 2d R r  . 【详解】 设球O的半径为 R，则 24 16R  ，解得： 2R  . 设 ABC 外接圆半径为 r，边长为 a， ABC 是面积为 9 3 4 的等边三角形， 21 3 9 3 2 2 4 a   ，解得： 3a  ， 2 22 2 99 3 3 4 3 4 ar a        ， 球心O到平面 ABC的距离 2 2 4 3 1d R r     . 故选：C. 【点睛】本题考查球的相关问题的求解，涉及到球的表面积公式和三角形面积公式的应用；解题关键是明 确球的性质，即球心和三角形外接圆圆心的连线必垂直于三角形所在平面. 9.（2020•全国 2卷）如图，已知三棱柱 ABC-A1B1C1的底面是正三角形，侧面 BB1C1C是矩形，M，N分别 为 BC，B1C1的中点，P为 AM上一点，过 B1C1和 P的平面交 AB于 E，交 AC于 F. （1）证明：AA1∥MN，且平面 A1AMN⊥EB1C1F； （2）设 O为△A1B1C1的中心，若 AO∥平面 EB1C1F，且 AO=AB，求直线 B1E与平面 A1AMN所成角的正弦 值. 【答案】（1）证明见解析；（2） 10 10 . 【解析】（1）由 ,M N分别为 BC， 1 1BC 的中点， 1//MN CC ，根据条件可得 1 1/ /AA BB ，可证 1MN AA// ， 要证平面 1 1EBC F 平面 1A AMN ，只需证明 EF 平面 1A AMN 即可； （2）连接 NP，先求证四边形ONPA是平行四边形，根据几何关系求得 EP，在 1 1BC 截取 1BQ EP ，由 （1） BC⊥平面 1A AMN ，可得 QPN 为 1B E与平面 1A AMN 所成角，即可求得答案. 【详解】（1） ,M N分别为BC， 1 1BC 的中点， 1//MN BB ,又 1 1/ /AA BB , 1//MN AA , 在 ABC 中，M 为 BC中点，则 BC AM ,又侧面 1 1BBCC为矩形， 1BC BB  , 1//MN BB ,MN BC ,由MN AM M  ， ,MN AM 平面 1A AMN ,  BC⊥平面 1A AMN ,又 1 1 //BC BC，且 1 1BC 平面 ABC，BC 平面 ABC， 1 1 //BC 平面 ABC ,又 1 1BC 平面 1 1EBC F ，且平面 1 1EBC F 平面 ABC EF , 1 1 / /BC EF , //EF BC ,又 BC  平面 1A AMN , EF 平面 1A AMN , EF  平面 1 1EBC F , 平面 1 1EBC F 平面 1A AMN , （2）连接 NP ,  //AO 平面 1 1EBC F ，平面 AONP平面 1 1EBC F NP , //AO NP , 根据三棱柱上下底面平行，其面 1A NMA平面 ABC AM ，面 1A NMA平面 1 1 1 1ABC AN ,  //ON AP ,故：四边形ONPA是平行四边形,设 ABC 边长是6m ( 0m  ), 可得：ON AP ， 6NP AO AB m   , O为 1 1 1A B C△ 的中心，且 1 1 1A B C△ 边长为6m ,  1 6 sin 60 3 3 ON m     ,故： 3ON AP m  , //EF BC , AP EP AM BM  ,  3 33 3 EP  ,解得： EP m ,在 1 1BC 截取 1BQ EP m  ，故 2QN m ,  1BQ EP 且 1 //BQ EP ,四边形 1BQPE是平行四边形， 1 //B E PQ , 由（1） 1 1BC 平面 1A AMN ,故 QPN 为 1B E与平面 1A AMN 所成角, 在 Rt QPN△ ，根据勾股定理可得：    2 22 2 2 6 2 10PQ QN PN m m m     2 10sin 102 10 QN mQPN PQ m      , 直线 1B E与平面 1A AMN 所成角的正弦值： 10 10 . 【点睛】本题主要考查了证明线线平行和面面垂直，及其线面角，解题关键是掌握面面垂直转为求证线面 垂直的证法和线面角的定义，考查了分析能力和空间想象能力，属于难题. 10.（2020•全国 3卷）下图为某几何体的三视图，则该几何体的表面积是（ ） A. 6+4 2 B. 4+4 2 C. 6+2 3 D. 4+2 3 【答案】C 【解析】根据三视图特征，在正方体中截取出符合题意的立体图形，求出每个面的面积，即可求得其表面 积. 【详解】根据三视图特征，在正方体中截取出符合题意的立体图形 根据立体图形可得： 1 2 2 2 2ABC ADC CDBS S S     △ △ △ 根据勾股定理可得： 2 2AB AD DB    ADB△ 是边长为 2 2的等边三角形 根据三角形面积公式可得： 21 1 3sin 60 (2 2) 2 3 2 2 2ADBS AB AD      △ 该几何体的表面积是： 2 3 6 2 33 2    .故选：C. 【点睛】本题主要考查了根据三视图求立体图形的表面积问题，解题关键是掌握根据三视图画出立体图形， 考查了分析能力和空间想象能力，属于基础题. 11.（2020•全国 3卷）已知圆锥的底面半径为 1，母线长为 3，则该圆锥内半径最大的球的体积为_________． 【答案】 2 3  【解析】将原问题转化为求解圆锥内切球的问题，然后结合截面确定其半径即可确定体积的值. 【详解】易知半径最大球为圆锥的内切球，球与圆锥内切时的轴截面如图所示， 其中 2, 3BC AB AC   ，且点 M为 BC边上的中点，设内切圆的圆心为O， 由于 2 23 1 2 2AM    ，故 1 2 2 2 2 2 2 S    △ABC ， 设内切圆半径为 r，则： ABC AOB BOC AOCS S S S  △ △ △ △ 1 1 1 2 2 2 AB r BC r AC r          1 3 3 2 2 2 2 r      ，解得： 2 2 r = ，其体积： 34 2 3 3 V r   . 故答案为： 2 3  . 【点睛】与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的 位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中 心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于 球的直径. 12.（2020•全国 3卷）如图，在长方体 1 1 1 1ABCD ABC D 中，点 ,E F分别在棱 1 1,DD BB 上，且 12DE ED ， 12BF FB ． （1）证明：点 1C 在平面 AEF 内； （2）若 2AB  ， 1AD  ， 1 3AA  ，求二面角 1A EF A  的正弦值． 【答案】（1）证明见解析；（2） 42 7 . 【解析】（1）连接 1C E 、 1C F ，证明出四边形 1AEC F 为平行四边形，进而可证得点 1C 在平面 AEF 内； （2）以点 1C 为坐标原点， 1 1C D 、 1 1C B 、 1CC所在直线分别为 x、 y、 z轴建立空间直角坐标系 1C xyz ， 利用空间向量法可计算出二面角 1A EF A  的余弦值，进而可求得二面角 1A EF A  的正弦值. 【详解】（1）在棱 1CC 上取点G，使得 1 1 2 CG CG ，连接DG、 FG、 1C E、 1C F， 在长方体 1 1 1 1ABCD ABC D 中， //AD BC且 AD BC ， 1 1//BB CC 且 1 1BB CC ， 1 1 2 CG CG ， 12BF FB ， 1 1 2 2 3 3 CG CC BB BF    且CG BF ， 所以，四边形 BCGF 为平行四边形，则 //AF DG 且 AF DG ， 同理可证四边形 1DECG为平行四边形， 1 //C E DG 且 1C E DG ， 1 //C E AF 且 1C E AF ，则四边形 1AEC F 为平行四边形， 因此，点 1C 在平面 AEF 内； （2）以点 1C 为坐标原点， 1 1C D 、 1 1C B 、 1CC所在直线分别为 x、 y、 z轴建立如下图所示的空间直角坐 标系 1C xyz ， 则  2,1,3A 、  1 2,1, 0A 、  2,0,2E 、  0,1,1F ，  0, 1, 1AE     ，  2,0, 2AF     ，  1 0, 1, 2A E    ，  1 2,0,1A F    ， 设平面 AEF 的法向量为  1 1 1, ,m x y z  ， 由 0 0 m AE m AF           ，得 1 1 1 1 0 2 2 0 y z x z       取 1 1z   ，得 1 1 1x y  ，则  1,1, 1m    ， 设平面 1AEF的法向量为  2 2 2, ,n x y z  ， 由 1 1 0 0 n A E n A F           ，得 2 2 2 2 2 0 2 0 y z x z       ，取 2 2z  ，得 2 1x  ， 2 4y  ，则  1,4,2n   ， 3 7cos , 73 21 m nm n m n            ， 设二面角 1A EF A  的平面角为，则 7cos 7   ， 2 42sin 1 cos 7      . 因此，二面角 1A EF A  的正弦值为 42 7 . 【点睛】本题考查点在平面的证明，同时也考查了利用空间向量法求解二面角角，考查推理能力与计算能 力，属于中等题. 13.（2020•江苏卷）如图，六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的．已知螺帽的底面正六边 形边长为 2 cm，高为 2 cm，内孔半轻为 0.5 cm，则此六角螺帽毛坯的体积是____cm. 【答案】12 3 2   【解析】先求正六棱柱体积，再求圆柱体积，相减得结果. 【详解】正六棱柱体积为 236 2 2=12 3 4    ,圆柱体积为 21( ) 2 2 2    所求几何体体积为12 3 2   ,故答案为： 12 3 2   【点睛】本题考查正六棱柱体积、圆柱体积，考查基本分析求解能力，属基础题. 14.（2020•江苏卷）在三棱柱 ABC-A1B1C1中，AB⊥AC，B1C⊥平面 ABC，E，F分别是 AC，B1C的中点． （1）求证：EF∥平面 AB1C1； （2）求证：平面 AB1C⊥平面 ABB1． 【答案】（1）证明详见解析；（2）证明详见解析. 【解析】（1）通过证明 1//EF AB ，来证得 //EF 平面 1 1ABC . （2）通过证明 AB 平面 1ABC，来证得平面 1ABC 平面 1ABB . 【详解】（1）由于 ,E F分别是 1,AC BC的中点，所以 1//EF AB . 由于 EF  平面 1 1ABC , 1AB 平面 1 1ABC ，所以 //EF 平面 1 1ABC . （2）由于 1BC 平面 ABC， ABÌ平面 ABC，所以 1BC AB . 由于 1,AB AC AC BC C   ，所以 AB 平面 1ABC , 由于 ABÌ平面 1ABB ，所以平面 1ABC 平面 1ABB . 【点睛】本小题主要考查线面平行的证明，考查面面垂直的证明，属于中档题. 15.（2020•新全国 1山东）日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子 来测定时间．把地球看成一个球(球心记为 O)，地球上一点 A的纬度是指 OA与地球赤道所在平面所成角， 点 A处的水平面是指过点 A且与 OA垂直的平面.在点 A处放置一个日晷，若晷面与赤道所在平面平行，点 A处的纬度为北纬 40°，则晷针与点 A处的水平面所成角为（ ） A. 20° B. 40° C. 50° D. 90° 【答案】B 【解析】画出过球心和晷针所确定的平面截地球和晷面的截面图，根据面面平行的性质定理和线面垂直的 定义判定有关截线的关系，根据点 A处的纬度，计算出晷针与点 A处的水平面所成角. 【详解】画出截面图如下图所示，其中CD是赤道所在平面的截线；l是点 A处的水平面的截线，依题意可 知OA l ；AB是晷针所在直线.m是晷面的截线，依题意依题意,晷面和赤道平面平行，晷针与晷面垂直， 根据平面平行的性质定理可得可知 //m CD、根据线面垂直的定义可得 AB m .. 由于 40 , //AOC m CD   ，所以 40OAG AOC   ， 由于 90OAG GAE BAE GAE     ， 所以 40BAE OAG   ，也即晷针与点 A处的水平面所成角为 40BAE   . 故选：B 【点睛】本小题主要考查中国古代数学文化，考查球体有关计算，涉及平面平行，线面垂直的性质，属于 中档题. 16.（2020•新全国 1山东）某中学开展劳动实习，学生加工制作零件，零件的截面如图所示．O为圆孔及轮 廓圆弧 AB所在圆的圆心，A是圆弧 AB与直线 AG的切点，B是圆弧 AB与直线 BC的切点，四边形 DEFG 为矩形，BC⊥DG，垂足为 C，tan∠ODC= 3 5 ， BH DG∥ ，EF=12 cm，DE=2 cm，A到直线 DE和 EF的 距离均为 7 cm，圆孔半径为 1 cm，则图中阴影部分的面积为________cm2． 【答案】 54 2  【解析】利用 3tan 5 ODC  求出圆弧 AB所在圆的半径，结合扇形的面积公式求出扇形 AOB的面积，求 出直角 OAH△ 的面积，阴影部分的面积可通过两者的面积之和减去半个单位圆的面积求得. 【详解】设  OB OA r，由题意 7AM AN  ， 12EF  ，所以 5NF  ， 因为 5AP  ,所以 45AGP   ，因为 / /BH DG，所以 45AHO   ， 因为 AG与圆弧 AB相切于 A点，所以OA AG ，即 OAH△ 为等腰直角三角形； 在直角 OQD△ 中， 25 2 OQ r  ， 27 2 DQ r  ， 因为 3tan 5 OQODC DQ    ，所以 3 2 5 221 25 2 2 r r   ，解得 2 2r  ； 等腰直角 OAH△ 的面积为 1 1 2 2 2 2 4 2 S     ；扇形 AOB的面积  22 1 3 2 2 3 2 4 S      ， 所以阴影部分的面积为 1 2 1 54 2 2 S S     .故答案为： 54 2   . 【点睛】本题主要考查三角函数在实际中应用，把阴影部分合理分割是求解的关键，以劳动实习为背景， 体现了五育并举的育人方针. 17.（2020•新全国 1山东）已知直四棱柱 ABCD–A1B1C1D1的棱长均为 2，∠BAD=60°．以 1D 为球心， 5为 半径的球面与侧面 BCC1B1的交线长为________． 【答案】 2 2  . 【解析】根据已知条件易得 1D E 3 ， 1D E 侧面 1 1BCCB，可得侧面 1 1BCCB与球面的交线上的点到 E 的距离为 2 ，可得侧面 1 1BCCB与球面的交线是扇形 EFG的弧FG，再根据弧长公式可求得结果. 【详解】如图： 取 1 1BC 的中点为 E， 1BB 的中点为 F ， 1CC 的中点为G， 因为 BAD  60°，直四棱柱 1 1 1 1ABCD ABC D 的棱长均为 2，所以△ 1 1 1D BC 为等边三角形，所以 1D E 3 ， 1 1 1D E BC ， 又四棱柱 1 1 1 1ABCD ABC D 为直四棱柱，所以 1BB 平面 1111 DCBA ，所以 1 1 1BB BC ， 因为 1 1 1 1BB BC B ，所以 1D E 侧面 1 1BCCB， 设 P为侧面 1 1BCCB与球面的交线上的点，则 1D E EP ， 因为球的半径为 5， 1 3D E  ，所以 2 2 1 1| | | | | | 5 3 2EP D P D E     ， 所以侧面 1 1BCCB与球面的交线上的点到 E的距离为 2 ， 因为 | | | | 2EF EG  ，所以侧面 1 1BCCB与球面的交线是扇形 EFG的弧FG， 因为 1 1 4 B EF C EG      ，所以 2 FEG    ， 所以根据弧长公式可得 22 2 2 FG     .故答案为： 2 2  . 【点睛】本题考查了直棱柱的结构特征，考查了直线与平面垂直的判定，考查了立体几何中的轨迹问题， 考查了扇形中的弧长公式，属于中档题. 18.（2020•新全国 1山东）如图，四棱锥 P-ABCD的底面为正方形，PD⊥底面 ABCD．设平面 PAD与平面 PBC的交线为 l． （1）证明：l⊥平面 PDC； （2）已知 PD=AD=1，Q为 l上的点，求 PB与平面 QCD所成角的正弦值的最大值． 【答案】（1）证明见解析；（2） 6 3 . 【解析】（1）利用线面垂直的判定定理证得 AD平面 PDC ，利用线面平行的判定定理以及性质定理，证 得 //AD l，从而得到 l 平面 PDC ； （2）根据题意，建立相应的空间直角坐标系，得到相应点的坐标，设出点 ( , 0,1)Q m ，之后求得平面QCD 的法向量以及向量 PB  的坐标，求得 cos ,n PB    的最大值，即为直线 PB与平面QCD所成角的正弦值的 最大值. 【详解】（1）证明： 在正方形 ABCD中， //AD BC， 因为 AD 平面 PBC，BC 平面 PBC，所以 //AD 平面 PBC， 又因为 AD平面 PAD，平面 PAD平面 PBC l ，所以 //AD l， 因为在四棱锥 P ABCD 中，底面 ABCD是正方形，所以 , ,AD DC l DC   且 PD 平面 ABCD，所以 , ,AD PD l PD   因为CD PD D 所以 l 平面 PDC ； （2）如图建立空间直角坐标系D xyz ， 因为 1PD AD  ，则有 (0,0,0), (0,1,0), (1,0,0), (0,0,1), (1,1,0)D C A P B ， 设 ( , 0,1)Q m ，则有 (0,1,0), ( ,0,1), (1,1, 1)DC DQ m PB       ， 设平面QCD的法向量为 ( , , )n x y z  ，则 0 0 DC n DQ n           ，即 0 0 y mx z     ， 令 1x  ，则 z m  ，所以平面QCD的一个法向量为 (1,0, )n m   ，则 2 1 0cos , 3 1 n PB mn PB n PB m              根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值，所以直线与 平面所成角的正弦值等于 2 |1 || cos , | 3 1 mn PB m      r uur 2 2 3 1 2 3 1 m m m      2 2 3 2 3 2 | | 3 61 1 1 1 3 1 3 1 3 3 m m m m             ，当且仅当 1m  时取等号， 所以直线 PB与平面QCD所成角的正弦值的最大值为 6 3 . 【点睛】该题考查的是有关立体几何的问题，涉及到的知识点有线面平行的判定和性质，线面垂直的判定 和性质，利用空间向量求线面角，利用基本不等式求最值，属于中档题目. 19.（2020•天津卷）若棱长为 2 3的正方体的顶点都在同一球面上，则该球的表面积为（ ） A. 12 B. 24 C. 36 D. 144 【答案】C 【解析】求出正方体的体对角线的一半，即为球的半径，利用球的表面积公式，即可得解. 【详解】这个球是正方体的外接球，其半径等于正方体的体对角线的一半， 即      2 2 2 2 3 2 3 2 3 3 2 R     ，所以，这个球的表面积为 2 24 4 3 36S R      .故选：C. 【点睛】本题考查正方体的外接球的表面积的求法，求出外接球的半径是本题的解题关键，属于基础题.求 多面体的外接球的面积和体积问题，常用方法有：（1）三条棱两两互相垂直时，可恢复为长方体，利用长 方体的体对角线为外接球的直径，求出球的半径；（2）直棱柱的外接球可利用棱柱的上下底面平行，借助 球的对称性，球心为上下底面外接圆的圆心连线的中点，再根据勾股定理求球的半径；（3）如果设计几何 体有两个面相交，可过两个面的外心分别作两个面的垂线，垂线的交点为几何体的球心. 20.（2020•天津卷）如图，在三棱柱 1 1 1ABC ABC 中， 1CC 平面 , , 2ABC AC BC AC BC   ， 1 3CC  ， 点 ,D E分别在棱 1AA 和棱 1CC 上，且 1 2,AD CE M  为棱 1 1A B 的中点． （Ⅰ）求证： 1 1C M B D ； （Ⅱ）求二面角 1B B E D  的正弦值； （Ⅲ）求直线 AB与平面 1DB E所成角的正弦值． 【答案】（Ⅰ）证明见解析；（Ⅱ） 30 6 ；（Ⅲ） 3 3 . 【解析】以C为原点，分别以 1, ,CA CB CC    的方向为 x轴， y轴， z轴的正方向建立空间直角坐标系. （Ⅰ）计算出向量 1C M  和 1B D  的坐标，得出 1 1 0C M B D    ，即可证明出 1 1C M B D ； （Ⅱ）可知平面 1BB E 的一个法向量为CA  ，计算出平面 1B ED的一个法向量为 n  ，利用空间向量法计算出 二面角 1B B E D  的余弦值，利用同角三角函数的基本关系可求解结果； （Ⅲ）利用空间向量法可求得直线 AB与平面 1DB E所成角的正弦值. 【详解】依题意，以C为原点，分别以CA  、CB  、 1CC  的方向为 x轴、 y轴、 z轴的正方向建立空间直角 坐标系（如图）， 可得  0,0,0C 、  2,0,0A 、  0,2,0B 、  1 0,0,3C 、  1 2,0,3A 、  1 0, 2,3B 、  2,0,1D 、  0,0, 2E 、  1,1,3M . （Ⅰ）依题意，  1 1,1,0C M   ，  1 2, 2, 2B D     ， 从而 1 1 2 2 0 0C M B D       ，所以 1 1C M B D ； （Ⅱ）依题意，  2,0,0CA   是平面 1BB E 的一个法向量，  1 0,2,1EB   ，  2,0, 1ED    ．设  , ,n x y z  为平面 1DB E的法向量， 则 1 0 0 n EB n ED           ，即 2 0 2 0 y z x z      ，不妨设 1x  ，可得  1, 1,2n    ． 2 6cos , 62 6C CA n A C n A n              ， 2 30sin , 1 cos , 6 CA n CA n           ．所以，二面角 1B B E D  的正弦值为 30 6 ； （Ⅲ）依题意，  2,2,0AB    ． 由（Ⅱ）知  1, 1,2n    为平面 1DB E的一个法向量，于是 4 3cos , 32 2 6 AB nAB n AB n              ． 所以，直线 AB与平面 1DB E所成角的正弦值为 3 3 . 【点睛】本题考查利用空间向量法证明线线垂直，求二面角和线面角的正弦值，考查推理能力与计算能力， 属于中档题. 21.（2020•浙江卷）某几何体的三视图（单位：cm）如图所示，则该几何体的体积（单位：cm3）是（ ） A. 7 3 B. 14 3 C. 3 D. 6 【答案】A 【解析】根据三视图还原原图，然后根据柱体和锥体体积计算公式，计算出几何体的体积. 【详解】由三视图可知，该几何体是上半部分是三棱锥，下半部分是三棱柱， 且三棱锥的一个侧面垂直于底面，且棱锥的高为 1，棱柱的底面为等腰直角三角形，棱柱的高为 2， 所以几何体的体积为： 1 1 1 1 72 1 1 2 1 2 2 3 2 2 3 3                      .故选：A 【点睛】本小题主要考查根据三视图计算几何体的体积，属于基础题. 22.（2020•浙江卷）已知圆锥展开图的侧面积为 2π，且为半圆，则底面半径为_______． 【答案】1 【解析】利用题目所给圆锥侧面展开图的条件列方程组，由此求得底面半径. 【详解】设圆锥底面半径为 r，母线长为 l，则 2 12 2 2 r l r l                ，解得 1, 2r l  . 故答案为：1 【点睛】本小题主要考查圆锥侧面展开图有关计算，属于基础题. 23.（2020•浙江卷）如图，三棱台 DEF—ABC中，面 ADFC⊥面 ABC，∠ACB=∠ACD=45°，DC =2BC． （I）证明：EF⊥DB； （II）求 DF与面 DBC所成角的正弦值． 【答案】（I）证明见解析；（II） 3 3 【解析】 【分析】（I）作DH AC 交 AC于 H ，连接 BH ，由题意可知DH 平面 ABC，即有DH BC ，根 据勾股定理可证得 BC BH ，又 / /EF BC ，可得 DH EF ， BH EF ，即得 EF 平面 BHD，即 证得 EF DB ； （II）由 / /DF CH ，所以DF与平面DBC所成角即为CH 与平面DBC所成角，作HG BD 于G，连 接CG ，即可知 HCG 即为所求角，再解三角形即可求出DF与平面DBC所成角的正弦值． 【详解】（Ⅰ）作DH AC 交 AC于H ，连接 BH ． ∵平面 ADFC 平面 ABC，而平面 ADFC 平面 ABC AC ，DH 平面 ADFC， ∴DH 平面 ABC，而 BC 平面 ABC，即有DH BC ． ∵ 45ACB ACD   ，∴ 2 2 2CD CH BC CH BC    ． 在 CBH 中， 2 2 2 22 cos45BH CH BC CH BC BC      ，即有 2 2 2BH BC CH  ，∴ BH BC ． 由棱台的定义可知， / /EF BC，所以DH EF ， BH EF ，而 BH DH H ， ∴ EF 平面 BHD，而 BD 平面 BHD，∴ EF DB ． （Ⅱ）因为 / /DF CH ，所以DF与平面DBC所成角即为与CH 平面DBC所成角． 作HG BD 于G，连接CG，由（1）可知， BC⊥平面 BHD， 因为所以平面 BCD 平面 BHD，而平面 BCD平面 BHD BD ， HG 平面 BHD，∴HG 平面 BCD． 即CH 在平面DBC内的射影为CG ， HCG 即为所求角． 在 Rt HGC△ 中，设 BC a ，则 2CH a ， 2 2 3 3 BH DH a aHG a BD a      ， ∴ 1 3sin 33 HGHCG CH     ． 故DF与平面DBC所成角的正弦值为 3 3 ． 【点睛】本题主要考查空间点、线、面位置关系，线面垂直的判定定理的应用，直线与平面所成的角的求 法，意在考查学生的直观想象能力和数学运算能力，属于基础题． 24.（2020•上海卷）在棱长为 10的正方体. 1 1 1 1ABCD ABC D 中，P为左侧面 1 1ADD A上一点，已知点P到 1 1AD 的距离为 3，点P到 1AA 的距离为 2，则过点P且与 1AC平行的直线交正方体于P、Q两点，则Q点 所在的平面是（ ） A. 1 1AAB B B. 1 1BBC C C. 1 1CC DD D. ABCD 【答案】D 【解析】延长 BC至M点，使得 =2CM ,延长 1CC至N 点，使得 3CN  , 以C M N、 、 为顶点作矩形，记矩形的另外一个顶点为H， 连接 1AP PH HC、 、 ，则易得四边形 1APHC为平行四边形， 因为点P在平面 1 1ADD A内，点H在平面 1 1BCC B 内， 且点P在平面 ABCD的上方，点H在平面 ABCD下方， 所以线段PH 必定会在和平面 ABCD相交， 即点Q在平面 ABCD内 25.（2020•上海卷）已知边长为 1的正方形 ABCD，沿 BC旋转一周得到圆柱体。 （1）求圆柱体的表面积； （2）正方形 ABCD 绕 BC逆时针旋转 2  到 1 1A BCD ，求 1AD 与平面 ABCD所成 的角。 【答案】（1）4π；（2） 3arcsin 3 10 平面解析几何 1.（2020•北京卷）已知半径为 1的圆经过点 (3,4)，则其圆心到原点的距离的最小值为（ ）． A. 4 B. 5 C. 6 D. 7 【答案】A 【解析】求出圆心C的轨迹方程后，根据圆心M 到原点O的距离减去半径 1可得答案. 【详解】设圆心  ,C x y ，则    2 23 4 1x y    ，化简得    2 23 4 1x y    ， 所以圆心C的轨迹是以 (3, 4)M 为圆心，1为半径的圆， 所以 | | 1 | |OC OM  2 23 4 5   ，所以 | | 5 1 4OC    ， 当且仅当C在线段OM 上时取得等号，故选：A. 【点睛】本题考查了圆的标准方程，属于基础题. 2.（2020•北京卷）设抛物线的顶点为O，焦点为 F ，准线为 l．P是抛物线上异于O的一点，过 P作 PQ l 于Q，则线段 FQ的垂直平分线（ ）． A. 经过点O B. 经过点 P C. 平行于直线OP D. 垂直于直线OP 【答案】B 【解析】依据题意不妨作出焦点在 x轴上的开口向右的抛物线，根据垂直平分线的定义和抛物线的定义可 知，线段 FQ的垂直平分线经过点 P，即求解. 【详解】如图所示： ． 因为线段 FQ的垂直平分线上的点到 ,F Q的距离相等，又点 P在抛物线上，根据定义可知， PQ PF ， 所以线段 FQ的垂直平分线经过点 P .故选：B. 【点睛】本题主要考查抛物线的定义的应用，属于基础题. 3.（2020•北京卷）已知双曲线 2 2 : 1 6 3 x yC   ，则 C的右焦点的坐标为_________；C的焦点到其渐近线的 距离是_________． 【答案】 (1).  3,0 (2). 3 【解析】根据双曲线的标准方程可得出双曲线C的右焦点坐标，并求得双曲线的渐近线方程，利用点到直 线的距离公式可求得双曲线的焦点到渐近线的距离. 【详解】在双曲线C中， 6a  ， 3b  ，则 2 2 3c a b   ，则双曲线C的右焦点坐标为  3,0 ， 双曲线C的渐近线方程为 2 2 y x  ，即 2 0x y  ， 所以，双曲线C的焦点到其渐近线的距离为 2 3 3 1 2   .故答案为：  3,0 ； 3 . 【点睛】本题考查根据双曲线的标准方程求双曲线的焦点坐标以及焦点到渐近线的距离，考查计算能力， 属于基础题. 4.（2020•北京卷）已知椭圆 2 2 2 2: 1x yC a b   过点 ( 2, 1)A   ，且 2a b ． （Ⅰ）求椭圆 C的方程： （Ⅱ）过点 ( 4,0)B  的直线 l交椭圆 C于点 ,M N ,直线 ,MA NA分别交直线 4x   于点 ,P Q．求 | | | | PB BQ 的 值． 【答案】（Ⅰ） 2 2 1 8 2 x y   ；（Ⅱ）1. 【解析】(Ⅰ)由题意得到关于 a,b的方程组，求解方程组即可确定椭圆方程； (Ⅱ)首先联立直线与椭圆的方程，然后由直线 MA,NA的方程确定点 P,Q的纵坐标，将线段长度的比值转化 为纵坐标比值的问题，进一步结合韦达定理可证得 0P Qy y  ，从而可得两线段长度的比值. 【详解】(1)设椭圆方程为：   2 2 2 2 1 0x y a b a b     ，由题意可得： 2 2 4 1 1 2 a b a b       ，解得： 2 2 8 2 a b     ，故椭圆方程为： 2 2 1 8 2 x y   . (2)设  1 1,M x y ，  2 2,N x y ，直线MN的方程为：  4y k x  ， 与椭圆方程 2 2 1 8 2 x y   联立可得：  22 24 4 8x k x   ，即：    2 2 2 24 1 32 64 8 0k x k x k     ， 则： 2 2 1 2 1 22 2 32 64 8, 4 1 4 1 k kx x x x k k        .直线 MA的方程为：  1 1 11 2 2 yy x x      ， 令 4x   可得：      1 11 1 1 1 1 1 4 1 2 1 41 22 1 2 2 2 2 2P k x k xy xy x x x x                    ， 同理可得：    2 2 2 1 4 2Q k x y x      .很明显 0P Qy y  ，且： P Q PB y PQ y  ，注意到：              1 2 2 11 2 1 2 1 2 4 2 4 24 42 1 2 1 2 2 2 2P Q x x x xx xy y k k x x x x                      ， 而：        1 2 2 1 1 2 1 24 2 4 2 2 3 8x x x x x x x x           2 2 2 2 64 8 322 3 8 4 1 4 1 k k k k                   2 2 2 2 64 8 3 32 8 4 1 2 0 4 1 k k k k           ， 故 0,P Q P Qy y y y    .从而 1P Q PB y PQ y   . 【点睛】解决直线与椭圆的综合问题时，要注意： (1)注意观察应用题设中的每一个条件，明确确定直线、椭圆的条件； (2)强化有关直线与椭圆联立得出一元二次方程后的运算能力，重视根与系数之间的关系、弦长、斜率、三 角形的面积等问题． 5.（2020•全国 1卷）已知 A为抛物线 C:y2=2px（p>0）上一点，点 A到 C的焦点的距离为 12，到 y轴的距 离为 9，则 p=（ ） A. 2 B. 3 C. 6 D. 9 【答案】C 【解析】利用抛物线的定义建立方程即可得到答案. 【详解】设抛物线的焦点为 F，由抛物线的定义知 | | 12 2A pAF x   ，即12 9 2 p   ，解得 6p = . 故选：C. 【点晴】本题主要考查利用抛物线的定义计算焦半径，考查学生转化与化归思想，是一道容易题. 6.（2020•全国 1卷）已知⊙M： 2 2 2 2 2 0x y x y     ，直线 l： 2 2 0x y   ， P为 l上的动点，过 点 P作⊙M的切线 ,PA PB，切点为 ,A B，当 | | | |PM AB 最小时，直线 AB的方程为（ ） A. 2 1 0x y   B. 2 1 0x y   C. 2 1 0x y   D. 2 1 0x y   【答案】D 【解析】由题意可判断直线与圆相离，根据圆的知识可知，四点 , , ,A P B M 共圆，且 AB MP ，根据 4 4PAMPM AB S PA   可知，当直线MP l 时， PM AB 最小，求出以MP为直径的圆的方程， 根据圆系的知识即可求出直线 AB的方程． 【详解】圆的方程可化为    2 21 1 4x y    ，点M 到直线 l的距离为 2 2 2 1 1 2 5 2 2 1 d        ，所以 直 线 l 与 圆 相 离 ． 依 圆 的 知 识 可 知 ， 四 点 , , ,A P B M 四 点 共 圆 ， 且 AB MP ， 所 以 14 4 4 2PAMPM AB S PA AM PA       ，而 2 4PA MP  ， 当直线MP l 时， min 5MP  ， min 1PA  ，此时 PM AB 最小． ∴  1: 1 1 2 MP y x   即 1 1 2 2 y x  ，由 1 1 2 2 2 2 0 y x x y         解得， 1 0 x y     ． 所以以MP为直径的圆的方程为      1 1 1 0x x y y     ，即 2 2 1 0x y y    ， 两圆的方程相减可得： 2 1 0x y   ，即为直线 AB的方程． 故选：D. 【点睛】本题主要考查直线与圆，圆与圆的位置关系的应用，以及圆的几何性质的应用，意在考查学生的 转化能力和数学运算能力，属于中档题． 7.（2020•全国 1卷）已知 F为双曲线 2 2 2 2: 1( 0, 0)x yC a b a b     的右焦点，A为 C的右顶点，B为 C上的点， 且 BF垂直于 x轴.若 AB的斜率为 3，则 C的离心率为______________. 【答案】2 【解析】根据双曲线的几何性质可知， 2bBF a  ， AF c a  ，即可根据斜率列出等式求解即可． 【详解】联立 2 2 2 2 2 2 2 1 x c x y a b a b c          ，解得 2 x c by a      ，所以 2bBF a  . 依题可得， 3 BF AF  ， AF c a  ，即   2 2 2 3 b c aa c a a c a      ，变形得 3c a a  ， 2c a , 因此，双曲线C的离心率为 2 .故答案为： 2． 【点睛】本题主要考查双曲线的离心率的求法，以及双曲线的几何性质的应用，属于基础题． 8.（2020•全国 1卷）已知 A、B分别为椭圆 E： 2 2 2 1x y a   （a>1）的左、右顶点，G为 E的上顶点， 8AG GB    ， P为直线 x=6上的动点，PA与 E的另一交点为 C，PB与 E的另一交点为 D． （1）求 E的方程； （2）证明：直线 CD过定点. 【答案】（1） 2 2 1 9 x y  ；（2）证明详见解析. 【解析】（1）由已知可得：  ,0A a ，  ,0B a ，  0,1G ，即可求得 2 1AG GB a     ，结合已知即可求 得： 2 9a  ，问题得解. （2）设  06,P y ，可得直线 AP的方程为：  0 3 9 yy x  ，联立直线 AP的方程与椭圆方程即可求得点C 的坐标为 2 0 0 2 2 0 0 3 27 6, 9 9 y y y y        ，同理可得点D的坐标为 2 0 0 2 2 0 0 3 3 2, 1 1 y y y y        ，即可表示出直线CD的方 程，整理直线CD的方程可得：   0 2 0 4 3 23 3 yy x y       ，命题得证. 【详解】（1）依据题意作出如下图象： 由椭圆方程 2 2 2: 1( 1)xE y a a    可得：  ,0A a ，  ,0B a ，  0,1G   ,1AG a  ，  , 1GB a    2 1 8AG GB a      ， 2 9a  椭圆方程为： 2 2 1 9 x y  （2）证明：设  06,P y ， 则直线 AP的方程为：    0 0 3 6 3 yy x     ，即：  0 3 9 yy x  联立直线 AP的方程与椭圆方程可得：   2 2 0 1 9 3 9 x y yy x         ，整理得：  2 2 2 2 0 0 09 6 9 81 0y x y x y     ，解得： 3x   或 2 0 2 0 3 27 9 yx y     将 2 0 2 0 3 27 9 yx y     代入直线  0 3 9 yy x  可得： 0 2 0 6 9 yy y   所以点C的坐标为 2 0 0 2 2 0 0 3 27 6, 9 9 y y y y        . 同理可得：点D的坐标为 2 0 0 2 2 0 0 3 3 2, 1 1 y y y y        直线CD的方程为： 0 0 2 2 2 0 00 0 2 22 2 0 00 0 2 2 0 0 6 2 9 12 3 3 3 27 3 31 1 9 1 y y y yy yy x y yy y y y                         ， 整理可得：       2 2 2 0 00 0 0 0 2 2 24 2 0 0 00 0 8 32 3 3 8 3 3 1 1 16 9 6 3 y yy y y yy x x y y yy y                     整理得：     0 0 0 22 2 00 0 4 2 4 3 3 23 3 3 3 y y yy x x yy y          故直线CD过定点 3 ,0 2       【点睛】本题主要考查了椭圆的简单性质及方程思想，还考查了计算能力及转化思想、推理论证能力，属 于难题. 9.（2020•全国 2卷）若过点（2，1）的圆与两坐标轴都相切，则圆心到直线 2 3 0x y   的距离为（ ） A. 5 5 B. 2 5 5 C. 3 5 5 D. 4 5 5 【答案】B 【解析】由题意可知圆心在第一象限，设圆心的坐标为  , , 0a a a  ，可得圆的半径为 a，写出圆的标准方 程，利用点  2,1 在圆上，求得实数 a的值，利用点到直线的距离公式可求出圆心到直线 2 3 0x y   的距 离. 【详解】由于圆上的点  2,1 在第一象限，若圆心不在第一象限， 则圆与至少与一条坐标轴相交，不合乎题意，所以圆心必在第一象限， 设圆心的坐标为  ,a a ，则圆的半径为 a，圆的标准方程为    2 2 2x a y a a    . 由题意可得    2 2 22 1a a a    ，可得 2 6 5 0a a   ，解得 1a  或 5a  ， 所以圆心的坐标为  1,1 或  5,5 ，圆心 到直线 的距离均为 1 2 1 1 3 2 5 55 d      ； 圆心 到直线 的距离均为 2 2 5 5 3 2 5 55 d      圆心到直线 2 3 0x y   的距离均为 2 2 5 55 d    ；所以，圆心到直线2 3 0x y   的距离为 2 5 5 . 故选：B. 【点睛】本题考查圆心到直线距离的计算，求出圆的方程是解题的关键，考查计算能力，属于中等题. 10.（2020•全国 2卷）设O为坐标原点，直线 x a 与双曲线 2 2 2 2: 1( 0, 0)x yC a b a b     的两条渐近线分别交 于 ,D E两点，若 ODE 的面积为 8，则C的焦距的最小值为（ ） A. 4 B. 8 C. 16 D. 32 【答案】B 【解析】因为 2 2 2 2: 1( 0, 0)x yC a b a b     ，可得双曲线的渐近线方程是 by x a   ，与直线 x a 联立方程求 得D，E两点坐标，即可求得 | |ED ，根据 ODE 的面积为8，可得 ab值，根据 2 22 2c a b  ，结合均 值不等式，即可求得答案. 【详解】 2 2 2 2: 1( 0, 0)x yC a b a b     双曲线的渐近线方程是 by x a   直线 x a 与双曲线 2 2 2 2: 1( 0, 0)x yC a b a b     的两条渐近线分别交于D， E两点 不妨设D为在第一象限，E在第四象限.联立 x a by x a     ，解得 x a y b    故 ( , )D a b ,联立 x a by x a      ，解得 x a y b     ,故 ( , )E a b , | | 2ED b  ODE 面积为： 1 2 8 2ODES a b ab   △ ,双曲线 2 2 2 2: 1( 0, 0)x yC a b a b     其焦距为 2 22 2 2 2 2 16 8c a b ab     ,当且仅当 2 2a b  取等号 C的焦距的最小值：8 ,故选：B. 【点睛】本题主要考查了求双曲线焦距的最值问题，解题关键是掌握双曲线渐近线的定义和均值不等式求 最值方法，在使用均值不等式求最值时，要检验等号是否成立，考查了分析能力和计算能力，属于中档题. 11.（2020•全国 2卷）已知椭圆 C1： 2 2 2 2 1x y a b   (a>b>0)的右焦点 F与抛物线 C2的焦点重合，C1的中心与 C2的顶点重合.过 F且与 x轴垂直的直线交 C1于 A，B两点，交 C2于 C，D两点，且|CD|= 4 3 |AB|. （1）求 C1的离心率； （2）设 M是 C1与 C2的公共点，若|MF|=5，求 C1与 C2的标准方程. 【答案】（1） 1 2 ；（2） 2 2 1 : 1 36 27 x yC   ， 2 2 : 12C y x . 【解析】（1）求出 AB 、 CD ，利用 4 3 CD AB 可得出关于 a、c的齐次等式，可解得椭圆 1C 的离心率 的值； （2）由（1）可得出 1C 的方程为 2 2 2 2 1 4 3 x y c c   ，联立曲线 1C 与 2C 的方程，求出点M 的坐标，利用抛物 线的定义结合 5MF  可求得c的值，进而可得出 1C 与 2C 的标准方程. 【详解】（1）  , 0F c ， AB x 轴且与椭圆 1C 相交于 A、 B两点， 则直线 AB的方程为 x c ，联立 2 2 2 2 2 2 2 1 x c x y a b a b c         ，解得 2 x c by a      ，则 22bAB a  ， 抛物线 2C 的方程为 2 4y cx ，联立 2 4 x c y cx    ，解得 2 x c y c     ， 4CD c  ， 4 3 CD AB ，即 284 3 bc a  ， 22 3b ac ，即 2 22 3 2 0c ac a   ，即 22 3 2 0e e   ， 0 1e Q ，解得 1 2 e  ，因此，椭圆 1C 的离心率为 1 2 ； （2）由（1）知 2a c ， 3b c ，椭圆 1C 的方程为 2 2 2 2 1 4 3 x y c c   ， 联立 2 2 2 2 2 4 1 4 3 y cx x y c c        ，消去 y并整理得 2 23 16 12 0x cx c   ，解得 2 3 x c 或 6x c  （舍去）， 由抛物线的定义可得 2 5 5 3 3 cMF c c    ，解得 3c  .因此，曲线 1C 的标准方程为 2 2 1 36 27 x y   ， 曲线 2C 的标准方程为 2 12y x . 【点睛】本题考查椭圆离心率的求解，同时也考查了利用抛物线的定义求抛物线和椭圆的标准方程，考查 计算能力，属于中等题. 12.（2020•全国 3卷）设O为坐标原点，直线 2x  与抛物线 C： 2 2 ( 0)y px p  交于D，E两点，若 OD OE ，则C的焦点坐标为（ ） A. 1 ,0 4       B. 1 ,0 2       C. (1,0) D. (2,0) 【答案】B 【解析】根据题中所给的条件OD OE ，结合抛物线的对称性，可知 4 DOx EOx      ，从而可以确 定出点D的坐标，代入方程求得 p的值，进而求得其焦点坐标，得到结果. 【详解】因为直线 2x  与抛物线 2 2 ( 0)y px p  交于 ,E D两点，且OD OE ， 根据抛物线的对称性可以确定 4 DOx EOx      ，所以  2,2D ， 代入抛物线方程 4 4p ，求得 1p  ，所以其焦点坐标为 1( ,0) 2 ，故选：B. 【点睛】该题考查的是有关圆锥曲线的问题，涉及到的知识点有直线与抛物线的交点，抛物线的对称性， 点在抛物线上的条件，抛物线的焦点坐标，属于简单题目. 13.（2020•全国 3卷）设双曲线 C： 2 2 2 2 1x y a b   （a>0，b>0）的左、右焦点分别为 F1，F2，离心率为 5．P 是 C上一点，且 F1P⊥F2P．若△PF1F2的面积为 4，则 a=（ ） A. 1 B. 2 C. 4 D. 8 【答案】A 【解析】根据双曲线的定义，三角形面积公式，勾股定理，结合离心率公式，即可得出答案. 【详解】 5c a  ， 5c a  ，根据双曲线的定义可得 1 2 2PF PF a  ， 1 2 1 2 1 | | 4 2PF F PF FS P  △ ，即 1 2| | 8PF PF  ， 1 2F P F P ，  2 22 1 2| | 2PF PF c   ，  2 2 1 2 1 22 4PF PF PF PF c     ，即 2 25 4 0a a   ，解得 1a  ， 故选：A. 【点睛】本题主要考查了双曲线的性质以及定义的应用，涉及了勾股定理，三角形面积公式的应用，属于 中档题. 14.（2020•全国 3卷）已知椭圆 2 2 2: 1(0 5) 25 x yC m m     的离心率为 15 4 ，A，B分别为C的左、右顶点． （1）求C的方程； （2）若点 P在C上，点Q在直线 6x  上，且 | | | |BP BQ ，BP BQ ，求 APQ 的面积． 【答案】（1） 2 216 1 25 25 x y   ；（2） 5 2 . 【解析】（1）因为 2 2 2: 1(0 5) 25 x yC m m     ，可得 5a  ，b m ，根据离心率公式，结合已知，即可求得 答案； （2）点 P在C上，点Q在直线 6x  上，且 | | | |BP BQ ，BP BQ ，过点 P作 x轴垂线，交点为M ，设 6x  与 x轴交点为 N ，可得 PMB BNQ△ △ ，可求得 P点坐标，求出直线 AQ的直线方程，根据点到 直线距离公式和两点距离公式，即可求得 APQ 的面积. 【详解】（1） 2 2 2: 1(0 5) 25 x yC m m      5a  ，b m ， 根据离心率 2 2 15 4 1 1 5 c b me a a                 ， 解得 5 4 m  或 5 4 m   (舍)，C的方程为： 2 2 2 1 4 25 5 x y         ，即 2 216 1 25 25 x y   ； （2）不妨设 P ,Q在 x轴上方 点 P在C上，点Q在直线 6x  上，且 | | | |BP BQ ，BP BQ ， 过点 P作 x轴垂线，交点为M ，设 6x  与 x轴交点为 N 根据题意画出图形，如图  | | | |BP BQ ，BP BQ ， 90PMB QNB   ，又 90PBM QBN   ， 90BQN QBN   ， PBM BQN  ，根据三角形全等条件“ AAS”， 可得： PMB BNQ△ △ ， 2 216 1 25 25 x y   ， (5,0)B ， 6 5 1PM BN    ， 设 P点为 ( , )P Px y ，可得 P点纵坐标为 1Py  ，将其代入 2 216 1 25 25 x y   ， 可得： 2 16 1 25 25 Px   ，解得： 3Px  或 3Px   ， P点为 (3,1)或 ( 3,1) ， ①当 P点为 (3,1)时，故 5 3 2MB    ， PMB BNQ△ △ ， | | | | 2MB NQ  ， 可得：Q点为 (6,2)，画出图象，如图  ( 5,0)A  , (6,2)Q ，可求得直线 AQ的直线方程为：2 11 10 0x y   ， 根据点到直线距离公式可得 P到直线 AQ的距离为： 2 2 2 3 11 1 10 5 5 51252 11 d         ， 根据两点间距离公式可得：    2 26 5 2 0 5 5AQ      ，  APQ 面积为： 1 5 55 5 2 5 2    ； ②当 P点为 ( 3,1) 时，故 5+3 8MB   ， PMB BNQ△ △ ，  | | | | 8MB NQ  ，可得：Q点为 (6,8)，画出图象，如图  ( 5,0)A  , (6,8)Q ，可求得直线 AQ的直线方程为：8 11 40 0x y   ， 根据点到直线距离公式可得 P到直线 AQ的距离为：   2 2 8 3 11 1 40 5 5 185 1858 11 d          ， 根据两点间距离公式可得：    2 26 5 8 0 185AQ      ，  APQ 面积为： 1 5 5185 2 2185    ，综上所述， APQ 面积为： 5 2 . 【点睛】本题主要考查了求椭圆标准方程和求三角形面积问题，解题关键是掌握椭圆的离心率定义和数形 结合求三角形面积，考查了分析能力和计算能力，属于中档题. 15.（2020•江苏卷）在平面直角坐标系 xOy中，若双曲线 2 2 x a ﹣ 2 5 y =1(a＞0)的一条渐近线方程为 y= 5 2 x， 则该双曲线的离心率是____. 【答案】 3 2 【解析】根据渐近线方程求得 a，由此求得c，进而求得双曲线的离心率. 【详解】双曲线 2 2 2 1 5 x y a   ，故 5b  .由于双曲线的一条渐近线方程为 5 2 y x ，即 5 2 2 b a a    ， 所以 2 2 4 5 3c a b     ，所以双曲线的离心率为 3 2 c a  .故答案为： 3 2 【点睛】本小题主要考查双曲线的渐近线，考查双曲线离心率的求法，属于基础题. 16.（2020•江苏卷）在平面直角坐标系 xOy中，已知 3( 0) 2 P ， ，A，B是圆 C： 2 21( ) 36 2 x y   上的两个动 点，满足 PA PB ，则△PAB面积的最大值是__________． 【答案】10 5 【解析】根据条件得 PC AB ,再用圆心到直线距离表示三角形 PAB面积，最后利用导数求最大值. 【详解】 PA PB PC AB  Q 设圆心C到直线 AB距离为 d ，则 2 3 1| |=2 36 ,| | 1 4 4 AB d PC    所以 2 2 21 2 36 ( 1) (36 )( 1) 2PABS d d d d      V 令 2 2 2(36 )( 1) (0 6) 2( 1)( 2 36) 0 4y d d d y d d d d              （负值舍去） 当 0 4d  时， 0y  ；当4 6d  时， 0y  ，因此当 4d  时，y取最大值，即 PABS 取最大值为10 5， 故答案为：10 5 【点睛】本题考查垂径定理、利用导数求最值，考查综合分析求解能力，属中档题. 17.（2020•江苏卷）在平面直角坐标系 xOy中，已知椭圆 2 2 : 1 4 3 x yE   的左、右焦点分别为 F1，F2，点 A 在椭圆 E上且在第一象限内，AF2⊥F1F2，直线 AF1与椭圆 E相交于另一点 B． （1）求△AF1F2的周长； （2）在 x轴上任取一点 P，直线 AP与椭圆 E的右准线相交于点 Q，求OP QP   的最小值； （3）设点 M在椭圆 E上，记△OAB与△MAB的面积分别为 S1，S2，若 S2=3S1，求点 M的坐标． 【答案】（1）6；（2）-4；（3）  2,0M 或 2 12, 7 7       . 【解析】（1）根据椭圆定义可得 1 2 4AF AF  ，从而可求出 1 2AF F△ 的周长； （2）设  0 ,0P x ，根据点 A在椭圆 E上，且在第一象限， 2 1 2AF FF ，求出 31, 2 A      ，根据准线方程得Q 点坐标，再根据向量坐标公式，结合二次函数性质即可出最小值； （3）设出设  1 1,M x y ，点M 到直线 AB的距离为 d ，由点O到直线 AB的距离与 2 13S S ，可推出 9 5 d  ， 根据点到直线的距离公式，以及  1 1,M x y 满足椭圆方程，解方程组即可求得坐标. 【详解】（1）∵椭圆 E的方程为 2 2 1 4 3 x y   ,∴  1 1,0F  ,  2 1,0F 由椭圆定义可得： 1 2 4AF AF  . ∴ 1 2AF F△ 的周长为 4 2 6  （2）设  0 ,0P x ，根据题意可得 0 1x  .∵点 A在椭圆E上，且在第一象限， 2 1 2AF FF ∴ 31, 2 A      ,∵准线方程为 4x  ,∴  4, QQ y , ∴        20 0 0 0 0,0 4, 4 2 4 4QOP QP x x y x x x              ，当且仅当 0 2x  时取等号. ∴OP QP   的最小值为 4 . （3）设  1 1,M x y ，点M 到直线 AB的距离为 d .∵ 31, 2 A      ，  1 1,0F  ∴直线 1AF 的方程为  3 1 4 y x  ,∵点O到直线 AB的距离为 3 5 ， 2 13S S ∴ 2 1 1 3 13 3 2 5 2 S S AB AB d       ,∴ 9 5 d  ,∴ 1 13 4 3 9x y   ① ∵ 2 2 1 1 1 4 3 x y   ②,∴联立①②解得 1 1 2 0 x y    ， 1 1 2 7 12 7 x y         . ∴  2,0M 或 2 12, 7 7       . 【点睛】本题考查了椭圆的定义，直线与椭圆相交问题、点到直线距离公式的运用，熟悉运用公式以及根 据 2 13S S 推出 9 5 d  是解答本题的关键. 18.（2020•新全国 1山东）已知曲线 2 2: 1C mx ny  .（ ） A. 若 m>n>0，则 C是椭圆，其焦点在 y轴上 B. 若 m=n>0，则 C是圆，其半径为 n C. 若 mn<0，则 C是双曲线，其渐近线方程为 my x n    D. 若 m=0，n>0，则 C是两条直线 【答案】ACD 【解析】结合选项进行逐项分析求解， 0m n  时表示椭圆， 0m n  时表示圆， 0mn  时表示双曲线， 0, 0m n  时表示两条直线. 【详解】对于 A，若 0m n  ，则 2 2 1mx ny  可化为 2 2 11 1 x y m n   ， 因为 0m n  ，所以 1 1 m n  ，即曲线C表示焦点在 y轴上的椭圆，故 A 正确； 对于 B，若 0m n  ，则 2 2 1mx ny  可化为 2 2 1x y n   ， 此时曲线C表示圆心在原点，半径为 n n 的圆，故 B 不正确； 对于 C，若 0mn  ，则 2 2 1mx ny  可化为 2 2 11 1 x y m n   ，此时曲线C表示双曲线， 由 2 2 0mx ny  可得 my x n    ，故 C正确； 对于 D，若 0, 0m n  ，则 2 2 1mx ny  可化为 2 1y n  ， ny n   ，此时曲线C表示平行于 x轴的两条直线，故 D 正确；故选：ACD. 【点睛】本题主要考查曲线方程的特征，熟知常见曲线方程之间的区别是求解的关键，侧重考查数学运算 的核心素养. 19.（2020•新全国 1山东）.斜率为 3的直线过抛物线 C：y2=4x的焦点，且与 C交于 A，B两点，则 AB =________． 【答案】 16 3 【解析】先根据抛物线的方程求得抛物线焦点坐标，利用点斜式得直线方程，与抛物线方程联立消去 y并 整理得到关于 x的二次方程，接下来可以利用弦长公式或者利用抛物线定义将焦点弦长转化求得结果. 【详解】∵抛物线的方程为 2 4y x ，∴抛物线的焦点 F坐标为 (1,0)F ， 又∵直线 AB过焦点 F且斜率为 3，∴直线 AB的方程为： 3( 1)y x  代入抛物线方程消去 y并化简得 23 10 3 0x x   ，解法一：解得 1 2 1 , 3 3 x x  所以 2 1 2 1 16| | 1 | | 1 3 | 3 | 3 3 AB k x x        解法二： 100 36 64 0     设 1 1 2 2( , ), ( , )A x y B x y ，则 1 2 10 3 x x  ,过 ,A B分别作准线 1x   的垂线，设垂足分别为 ,C D如图所示. 1 2| | | | | | | | | | 1 1AB AF BF AC BD x x        1 2 16+2= 3 x x  故答案为： 16 3 【点睛】本题考查抛物线焦点弦长，涉及利用抛物线的定义进行转化，弦长公式，属基础题. 20.（2020•新全国 1山东）已知椭圆 C： 2 2 2 2 1( 0)x y a b a b     的离心率为 2 2 ，且过点 A（2，1）． （1）求 C的方程： （2）点 M，N在 C上，且 AM⊥AN，AD⊥MN，D为垂足．证明：存在定点 Q，使得|DQ|为定值． 【答案】（1） 2 2 1 6 3 x y   ；（2）详见解析. 【解析】(1)由题意得到关于 a,b,c的方程组，求解方程组即可确定椭圆方程. (2)设出点 M，N的坐标，在斜率存在时设方程为 y kx m  , 联立直线方程与椭圆方程，根据已知条件， 已得到 m,k的关系，进而得直线 MN恒过定点，在直线斜率不存在时要单独验证，然后结合直角三角形的 性质即可确定满足题意的点 Q的位置. 【详解】(1)由题意可得： 2 2 2 2 2 3 2 4 1 1 c a a b a b c            ，解得： 2 2 26, 3a b c   ，故椭圆方程为： 2 2 1 6 3 x y   . (2)设点    1 1 2 2, , ,M x y N x y .因为 AM⊥AN，∴ · 0AM AN    ，即      1 2 1 22 2 1 1 0x x y y      ,① 当直线MN的斜率存在时，设方程为 y kx m  ,如图 1. 代入椭圆方程消去 y并整理得：  2 2 21 2k 4 2 6 0x kmx m     , 2 1 2 1 22 2 4 2 6, 1 2 1 2 km mx x x x k k        ②, 根据 1 1 2 2,y kx m y kx m    ,代入①整理可得：        22 1 2 1 2k 1 x 2 1 4 0x km k x x m         将②代入，       2 22 2 2 2 6 4k 1 2 1 4 0 1 2 1 2 m kmkm k m k k               ， 整理化简得    2 3 1 2 1 0k m k m     ,∵ 2,1A（ ）不在直线MN上，∴ 2 1 0k m   ， ∴ 2 3 1 0 1k m k   ， ，于是 MN的方程为 2 1 3 3 y k x       ， 所以直线过定点直线过定点 2 1, 3 3 E      . 当直线 MN的斜率不存在时，可得  1 1,N x y ,如图 2. 代入      1 2 1 22 2 1 1 0x x y y      得  2 2 1 22 1 0x y    , 结合 2 2 1 1 1 6 3 x y   ,解得  1 1 22 , 3 x x 舍 ,此时直线 MN过点 2 1, 3 3 E      , 由于 AE为定值，且△ADE为直角三角形，AE为斜边， 所以 AE中点 Q满足 QD 为定值（AE长度的一半 2 21 2 1 4 22 1 2 3 3 3               ）. 由于   2 1, 3 2,1 3 ,A E      ，故由中点坐标公式可得 4 1, 3 3 Q      . 故存在点 4 1, 3 3 Q      ，使得|DQ|为定值. 【点睛】本题考查椭圆的标准方程和性质，圆锥曲线中的定点定值问题，关键是第二问中证明直线 MN经 过定点，并求得定点的坐标,属综合题，难度较大. 21.（2020•天津卷）设双曲线C的方程为 2 2 2 2 1( 0, 0)x y a b a b     ，过抛物线 2 4y x 的焦点和点 (0, )b 的直 线为 l．若C的一条渐近线与 l平行，另一条渐近线与 l垂直，则双曲线C的方程为（ ） A. 2 2 1 4 4 x y   B. 2 2 1 4 yx   C. 2 2 1 4 x y  D. 2 2 1x y  【答案】D 【解析】由抛物线的焦点  1,0 可求得直线 l的方程为 1yx b   ，即得直线的斜率为 b ，再根据双曲线的 渐近线的方程为 by x a   ，可得 bb a    ， 1bb a     即可求出 ,a b，得到双曲线的方程． 【详解】由题可知，抛物线的焦点为  1,0 ，所以直线 l的方程为 1yx b   ，即直线的斜率为 b ， 又双曲线的渐近线的方程为 by x a   ，所以 bb a    ， 1bb a     ，因为 0, 0a b  ，解得 1, 1a b  ． 故选：D． 【点睛】本题主要考查抛物线的简单几何性质，双曲线的几何性质，以及直线与直线的位置关系的应用， 属于基础题． 22.（2020•天津卷）已知直线 3 8 0x y   和圆 2 2 2 ( 0)x y r r   相交于 ,A B两点．若 | | 6AB  ，则 r 的值为_________． 【答案】5 【解析】根据圆的方程得到圆心坐标和半径，由点到直线的距离公式可求出圆心到直线的距离 d ，进而利 用弦长公式 2 2| | 2AB r d  ，即可求得 r． 【详解】因为圆心  0,0 到直线 3 8 0x y   的距离 8 4 1 3 d    ， 由 2 2| | 2AB r d  可得 2 26 2 4r  ，解得 = 5r ．故答案为：5． 【点睛】本题主要考查圆的弦长问题，涉及圆的标准方程和点到直线的距离公式，属于基础题． 23.（2020•天津卷）已知椭圆 2 2 2 2 1( 0)x y a b a b     的一个顶点为 (0, 3)A  ，右焦点为 F ，且 | | | |OA OF ， 其中O为原点． （Ⅰ）求椭圆的方程； （Ⅱ）已知点C满足3OC OF   ，点 B在椭圆上（ B异于椭圆的顶点），直线 AB与以C为圆心的圆相切 于点 P，且 P为线段 AB的中点．求直线 AB的方程． 【答案】（Ⅰ） 2 2 1 18 9 x y   ；（Ⅱ） 1 3 2 y x  ，或 3y x  ． 【解析】（Ⅰ）根据题意，并借助 2 2 2a b c  ，即可求出椭圆的方程； （Ⅱ）利用直线与圆相切，得到CP AB ，设出直线 AB的方程，并与椭圆方程联立，求出 B点坐标，进 而求出 P点坐标，再根据CP AB ，求出直线 AB的斜率，从而得解. 【详解】（Ⅰ）椭圆   2 2 2 2 1 0x y a b a b     的一个顶点为  0, 3A  ，  3b  ，由 OA OF ，得 3c b  ，又由 2 2 2a b c  ，得 2 2 2 83 13a    ， 所以，椭圆的方程为 2 2 1 18 9 x y   ； （Ⅱ）直线 AB与以C为圆心的圆相切于点 P，所以CP AB ， 根据题意可知，直线 AB和直线CP的斜率均存在， 设直线 AB的斜率为 k，则直线 AB的方程为 3y kx+ = ，即 3y kx  ， 2 2 3 1 18 9 y kx x y       ，消去 y，可得  2 22 1 12 0k x kx   ，解得 0x  或 2 12 2 1 kx k   . 将 2 12 2 1 kx k   代入 3y kx  ，得 2 2 2 12 6 3 2 1 2 1 3 k y k k k k       ， 所以，点 B的坐标为 2 2 2 12 6 3, 2 1 2 1 k k k k       ，因为 P为线段 AB的中点，点 A的坐标为  0, 3 ， 所以点 P的坐标为 2 2 6 3, 2 1 2 1 k k k       ，由3OC OF   ，得点C的坐标为  1,0 ， 所以，直线CP的斜率为 2 2 2 3 0 32 1 6 2 6 11 2 1 CP k k k k k k         ，又因为CP AB ，所以 2 3 1 2 6 1 k k k      ， 整理得 22 3 1 0k k   ，解得 1 2 k  或 1k  .所以，直线 AB的方程为 1 3 2 y x  或 3y x  . 【点睛】本题考查了椭圆标准方程的求解、直线与椭圆的位置关系、直线与圆的位置关系、中点坐标公式 以及直线垂直关系的应用，考查学生的运算求解能力，属于中档题.当看到题目中出现直线与圆锥曲线位置 关系的问题时，要想到联立直线与圆锥曲线的方程. 24.（2020•浙江卷）已知点 O（0，0），A（–2，0），B（2，0）．设点 P满足|PA|–|PB|=2，且 P为函数 y= 23 4 x 图像上的点，则|OP|=（ ） A. 22 2 B. 4 10 5 C. 7 D. 10 【答案】D 【解析】根据题意可知，点 P既在双曲线的一支上，又在函数 23 4y x  的图象上，即可求出点 P的坐 标，得到 OP 的值． 【详解】因为 | | | | 2 4PA PB   ，所以点 P在以 ,A B为焦点，实轴长为 2，焦距为4的双曲线的右支上， 由 2, 1c a  可得， 2 2 2 4 1 3b c a     ，即双曲线的右支方程为   2 2 1 0 3 yx x   ，而点 P 还在函数 23 4y x  的图象上，所以， 由   2 2 2 1 0 3 3 4 yx x y x          ，解得 13 2 3 3 2 x y      ，即 13 27 10 4 4 OP    ．故选：D. 【点睛】本题主要考查双曲线的定义的应用，以及二次曲线的位置关系的应用，意在考查学生的数学运算 能力，属于基础题． 25.（2020•浙江卷）设直线 : ( 0)l y kx b k   ，圆 2 2 1 : 1C x y  ， 2 2 2 : ( 4) 1C x y   ，若直线 l与 1C ， 2C 都相切，则 k  _______；b=______． 【答案】 (1). 3 3 (2). 2 3 3  【解析】由直线与圆 1 2,C C 相切建立关于 k，b的方程组，解方程组即可. 【详解】由题意， 1 2,C C 到直线的距离等于半径，即 2 2 | | 1 1 b k   ， 2 2 | 4 | 1 1 k b k    ， 所以 | | 4b k b  ，所以 0k  （舍）或者 2b k  ， 解得 3 2 3, 3 3 k b   .故答案为： 3 2 3; 3 3  【点晴】本题主要考查直线与圆的位置关系，考查学生的数学运算能力，是一道基础题. 26.（2020•浙江卷）如图，已知椭圆 2 2 1 : 1 2 xC y  ，抛物线 2 2 : 2 ( 0)C y px p  ，点 A是椭圆 1C 与抛物 线 2C 的交点，过点 A的直线 l交椭圆 1C 于点 B，交抛物线 2C 于 M（B，M不同于 A）． （Ⅰ）若 1 16 p ，求抛物线 2C 的焦点坐标； （Ⅱ）若存在不过原点的直线 l使 M为线段 AB的中点，求 p的最大值． 【答案】（Ⅰ） 1( ,0) 32 ；（Ⅱ） 10 40 【解析】 【详解】（Ⅰ）当 1 16 p 时， 2C 的方程为 2 1 8 y x ，故抛物线 2C 的焦点坐标为 1( ,0) 32 ； （Ⅱ）设      1 1 2 2 0 0, , , , , , :A x y B x y M x y I x y m  ， 由   2 2 2 2 22 2 2 2 2 0 x y y my m x y m               ， 1 2 0 0 02 2 2 2 2, , 2 2 2 m m my y y x y m                  ， 由M 在抛物线上，所以   2 2 2 2 2 22 4 4 2 22 m pm m p         ， 又 2 2 22 2 ( ) 2 2 0 y px y p y m y p y pm x y m               ， 01 2y y p   ， 2 1 0 1 0 2 2x x y m y m p m          ， 2 1 2 22 2 2 mx p m       .由 2 2 2 2 1 4 2,  2 2 x y x px y px         即 2 4 2 0x px   2 2 1 4 16 8 2 4 2 2 p px p p         2 2 2 2 2 2 1 82 4 2 2 2 2 8 16 2 pp p p m p p p                 ， 所以 24 2 18p p  ， 2 1 160 p  ， 10 40 p  ， 所以， p的最大值为 10 40 ，此时 2 10 5( , ) 5 5 A . 法 2：设直线 : ( 0, 0)l x my t m t    ，  0 0,A x y . 将直线 l的方程代入椭圆 2 2 1 : 1 2 xC y  得：  2 2 22 2 2 0m y mty t     ， 所以点M 的纵坐标为 2 2M mty m    . 将直线 l的方程代入抛物线 2 2 : 2C y px 得： 2 2 2 0y pmy pt   ， 所以 0 2My y pt  ，解得  2 0 2 2p m y m   ，因此  22 0 2 2 2p m x m   ， 由 2 20 0 1 2 x y  解得 2 2 2 1 2 24 2 160m m p m m               … ， 所以当 102, 5 m t  时， p取到最大值为 10 40 . 【点晴】本题主要考查直线与圆锥曲线的位置关系的综合应用，涉及到求函数的最值，考查学生的数学运 算能力，是一道有一定难度的题. 27.（2020•上海卷）椭圆 2 2 1 4 3 x y   ，过右焦点 F 作直线 l交椭圆于 P、Q 两点，P 在第二象限已知    , , ' ' , 'Q Q Q QQ x y Q x y 都在椭圆上，且 y' 0Q Qy   ， 'FQ PQ ，则直线 l的方程为 【答案】 1 0x y   28.（2020•上海卷）双曲线 2 2 1 2 2: 1 4 x yC b   ，圆 2 2 2 2 : 4 ( 0)C x y b b    在第一 象限交点为 A， ( , )A AA x y ，曲线 2 2 2 2 2 2 1, 4 4 , A A x y x x b x y b x x           。 （1）若 6Ax  ，求 b； （2）若 b 5 ， 2C 与 x 轴交点记为 1 2F F、 ,P 是曲线上一点，且在第一象限，并满足 1 8PF  ，求 ∠ 1 2FPF ； （3）过点 2 (0, 2 ) 2 bS  且斜率为 2 b  的直线 l交曲线于M、N两点，用 b的代数式表示 ，并求出 的取值范围。 【答案】（1）2；（2） 11 16 ；（3） (6 2 5, )  ； 【解析】（1）若 6Ax  ，因为点 A为曲线 1C 与曲线 2C 的交点， ∵ 2 2 2 2 2 2 1 4 4 A A x y b x y b         ，解得 2 2 y b     ，∴ 2b  （2）方法一：由题意易得 1 2F F、 为曲线的两焦点，由双曲线定义知： 2 1 2PF PF a  ， 1 8,2 4PF a  ，∴ 2 4PF  又∵ 5b  ，∴ 1 2 6FF  在 1 2PF F 中由余弦定理可得： 2 2 2 1 2 1 2 1 2 1 2 11cos 2 16 PF PF F F F PF PF PF        方法二：∵ 5b  ，可得 2 2 2 2 1 4 5 ( 3) 64 x y x y         ，解得 (4, 15)P ， （3）设直线 2 4: 2 2 b bl y x     , 可得原点 O到直线 l的距离 2 2 2 2 2 4 42 4 41 4 b b d b b b         所以直线 l是圆的切线，切点为M, 所以 2 OMk b  ，并设 2:OMl y x b  ，与圆 2 2 24x y b   联立可得 2 2 2 2 4 4x x b b    ， 所以得 , 2x b y  ，即 ( , 2)M b ，注意到直线 l与双曲线得斜率为负得渐近线平行， 所以只有当 2Ay  时，直线 l才能与曲线有两个交点， 由 2 2 2 2 2 2 1 4 4A x y b x y b         ，得 4 2 2A by a b   ， 所以有 4 24 4 b b   ，解得 2 2 2 5b   ，或 2 2 2 5b   （舍） 又因为 由 上的投影可知： 所以